Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Веб-квест для учащихся 9-11 классов по теме "Теория вероятностей"
Содержание
- 1. Веб-квест для учащихся 9-11 классов по теме "Теория вероятностей"
- 2. Карта квестаПознакомьтесь, что же это за наука
- 3. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыОсновные виды задачИтогРеши самостоятельноПроверь
- 4. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыВведениеОсновные виды задачРеши самостоятельноПроверь
- 5. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогВечные истины
- 6. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогАлгоритм решения типовых задач:
- 7. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогСправочные материалыКлассическое определение вероятности:Вероятностью
- 8. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогСправочные материалыОсновные понятия теории
- 9. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогСправочные материалыНекоторые свойства :а)
- 10. ГлавнаяВведениеВечные истиныАлгоритм решения Справочные материалыИтогСправочные материалыОсновные понятия
- 11. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогСправочные материалыСочетаниями называются все
- 12. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогСправочные материалыРазмещениями из m
- 13. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогСправочные материалыКомбинация из n
- 14. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогСправочные материалыИзучи самостоятельно: Вероятность
- 15. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогРебусыОсновные виды задачПроверь себяРеши самостоятельноРебусы
- 16. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогПроверь себя:Основные виды задачПроверь
- 17. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогОсновные виды задачОсновные виды
- 18. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогОсновные виды задачОсновные виды
- 19. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогОсновные виды задачОсновные виды
- 20. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогОсновные виды задачОсновные виды
- 21. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогОсновные виды задачОсновные виды
- 22. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогОсновные виды задачОсновные виды
- 23. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогОсновные виды задачОсновные виды
- 24. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогОсновные виды задачОсновные виды
- 25. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогОсновные виды задачОсновные виды
- 26. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогОсновные виды задачОсновные виды
- 27. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогОсновные виды задачОсновные виды
- 28. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыИтогОсновные виды задачОсновные виды
- 29. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыКлассическое определение вероятностиСложение и
- 30. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыКлассическое определение вероятности:Задача №
- 31. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыСложение и умножение верятностей:Задача
- 32. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыРебусыСлучайные события:Задача № 1
- 33. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыРебусыКомбинаторика:Задача № 1 Из
- 34. ГлавнаяВведениеВечные истиныАлгоритм решенияСправочные материалыРебусы«На удачу»:Задача № 1
- 35. «Теория вероятностей есть в сущности
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1«Число, место и комбинация – три взаимно перекрещивающиеся, но отличные
сферы мышления, к которым можно отнести все математические идеи»
Слайд 2Карта квеста
Познакомьтесь, что же это за наука теория вероятностей.
Изучите
справочные материалы, алгоритм решения задач и ответьте на вопросы из
раздела «Проверь себя».Войдите в раздел «Основные виды задач» и начинайте изучать решение задач.
Если Вам недостаточно изложенного теоретического материала, то в разделе «Справочный материал» есть кнопка , которая отправит Вас на Интернет ресурс за необходимой информацией.
Теперь вы готовы к рассмотрению решения по формуле основных типов задач, встречающихся в ГИА – 9 и ЕГЭ - 11 по математике.
Если все получилось, переходите к разделу «Реши самостоятельно». Выберите тему с задачами и дерзайте!
В разделе «Ребусы» разгадайте пять ребусов по изученной теме.
В разделах «Справочный материал» и «Основные виды задач» переход на следующие слайды осуществляется с помощью кнопок
Удачи!
«Теория вероятностей»
Слайд 3Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Основные виды задач
Итог
Реши самостоятельно
Проверь себя
Предмет: математика
Тема: Теория
вероятностей
Учитель: Эдольф С.В.
Ребусы
Веб-квест для учащихся 9-11 классов по теме «Теория
вероятностей»Слайд 4Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Введение
Основные виды задач
Реши самостоятельно
Проверь себя
Итог
Ребята, в ГИА и ЕГЭ входят задачи по теории вероятностей.
Вам предстоит самостоятельно научиться решать задачи по этой теме. Предложенный квест – это самоучитель, который снабжен необходимым справочным материалом для решения задач.
С помощью квеста вы сможете подробно разобрать приведенные примеры и проверить себя с помощью предложенной схемы решения.
Подробно изучив предложенный материал, вам предстоит самостоятельно решить предложенные задачи.
Ребусы
«Теория вероятностей»
Слайд 5Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Вечные истины
Математику многие
любят за ее вечные истины: дважды два всегда четыре, сумма
четных чисел четна, а площадь прямоугольника равна произведению его смежных сторон. В любой задаче, которую мы решаем на уроках математики, у всех получается один и тот же ответ – нужно только не делать ошибок в решении.Реальная жизнь оказывается не такой простой и однозначной. Исходы многих явлений невозможно предсказать заранее, какой бы полной информацией мы о них не располагали. Нельзя, например, сказать наверняка, какой стороной упадет брошенная вверх монета, когда в следующем году выпадет первый снег или сколько человек в городе захотят в течение ближайшего часа позвонить по телефону. Такие непредсказуемые явления называются случайными.
Однако случай тоже имеет свои законы, которые начинают проявляться при многократном повторении случайных явлений. Именно такие закономерности изучаются в специальном разделе математики – Теории вероятностей.
Методы теории вероятностей широко применяются в различных отраслях науки и техники: в теории надёжности, теории массового обслуживания, теоретической физике, геодезии, астрономии, теории ошибок, теории управления, теории связи и во многих других теоретических и прикладных науках. Теория вероятностей служит для обоснования математической статистики.
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
«Теория вероятностей»
Слайд 6Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Алгоритм решения типовых задач:
Внимательно прочитать задачу
и понять, что именно происходит (что из какого
ящика вытаскивается, что где лежало, сколько приборов работает и т.п.) Найти основной вопрос задачи вроде "вычислить вероятность того, что ..." и вот
это многоточие записать в виде события, вероятность которого надо найти.
Событие записано. Теперь надо понять, к какой "схеме" теории вероятностей
относится задача, чтобы правильно выбрать формулы для решения. Ответьте на
тестовые вопросы типа:
происходит одно испытание (например, выбрасывание двух костей) или
несколько (например, проверка 10 приборов);
если испытаний несколько, зависимы ли результаты одного от других
(зависимость или независимость событий);
событие происходит в единственной ситуации или задача говорит о
нескольких возможных гипотезах (например, шар вынимается из любого
ящика из трех, или из конкретного).
Чем больше опыт решения задач, тем легче будет определить, какие формулы подходят.
Выбрана формула (или несколько) для решения. Записываем все данные задачи
и подставляем в данную формулу.
Вуаля, вероятность найдена.
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
«Теория вероятностей»
Слайд 7Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Справочные материалы
Классическое определение вероятности:
Вероятностью события А называется
отношение числа благоприятных для него исходов испытания к числу всех
равновозможных исходов.
где m - число исходов, благоприятствующих
осуществлению события,
а n - число всех возможных исходов.
Проверь себя
Основные виды задач
Реши самостоятельно
Ребусы
«Теория вероятностей»
Слайд 8Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Справочные материалы
Основные понятия теории вероятностей:
Наблюдаемые события можно
разделить на три вида: достоверные, невозможные и случайные.
Событие называется
достоверным, если оно обязательно произойдет при выполнении данного ряда условий. Например: При подбрасывании игрального кубика выпадет число меньшее 7.
Событие называется невозможным, если оно заведомо не произойдет при выполнении данного ряда условий.
Например: При подбрасывании игрального кубика выпадет число 7.
Событие называется случайным, если при осуществлении ряда условий оно может либо произойти, либо не
произойти.
Например: При подбрасывании игрального кубика
выпадет число 6.
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
«Теория вероятностей»
Слайд 9Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Справочные материалы
Некоторые свойства :
а) вероятность достоверного события
равна единице;
б) вероятность невозможного события равна нулю;
в) вероятность случайного события
есть положительное число, заключенноемежду нулем и единицей;
г) вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B).
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
«Теория вероятностей»
Слайд 10Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Справочные материалы
Основные понятия комбинаторики:
В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные
с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств.В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
«Теория вероятностей»
Слайд 11Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Справочные материалы
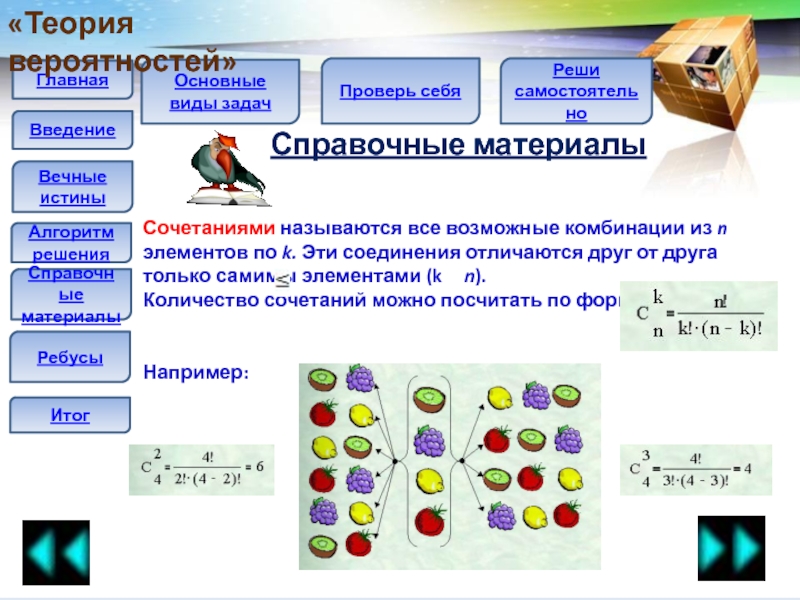
Сочетаниями называются все возможные комбинации из
n элементов по k. Эти соединения отличаются друг от друга
только самимы элементами (k n).Количество сочетаний можно посчитать по формуле:
Например:
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
«Теория вероятностей»
Слайд 12Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Справочные материалы
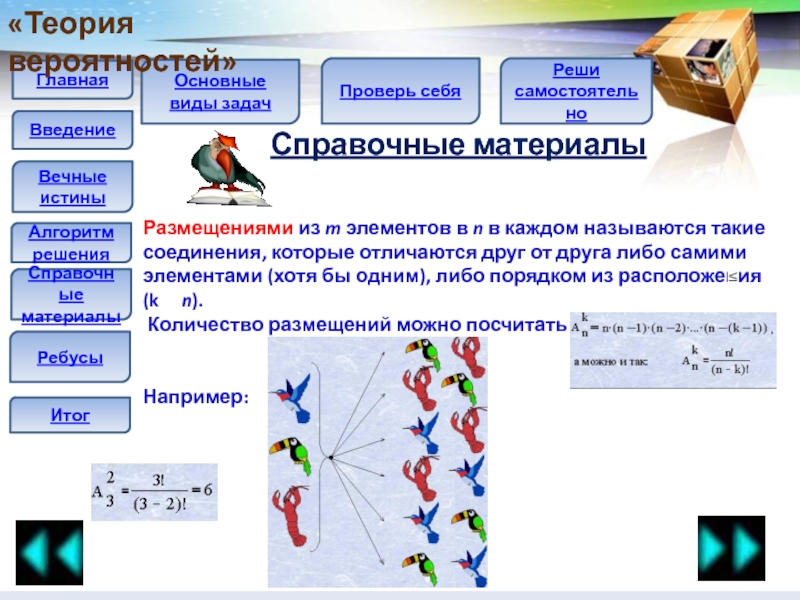
Размещениями из m элементов в n
в каждом называются такие соединения, которые отличаются друг от друга
либо самими элементами (хотя бы одним), либо порядком из расположения (k n).Количество размещений можно посчитать по формуле:
Например:
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
«Теория вероятностей»
Слайд 13Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Справочные материалы
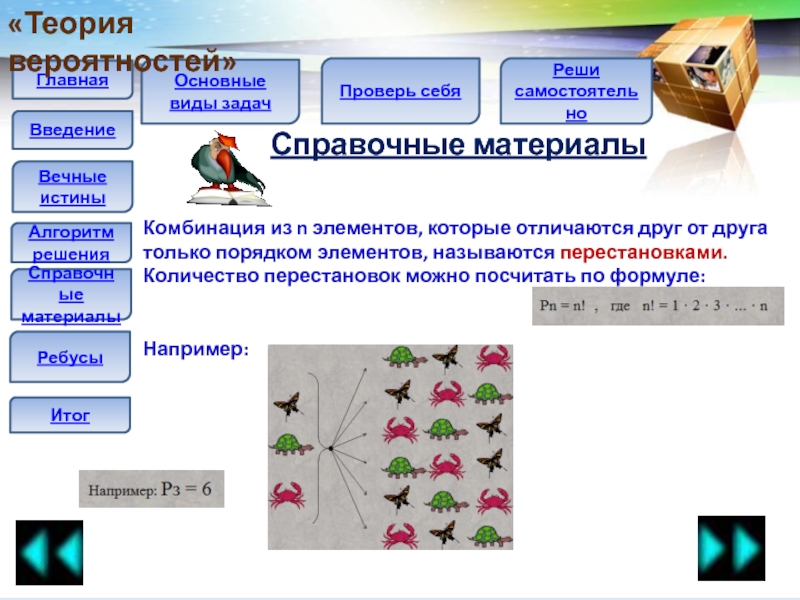
Комбинация из n элементов, которые отличаются
друг от друга только порядком элементов, называются перестановками.
Количество перестановок можно
посчитать по формуле:Например:
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
«Теория вероятностей»
Слайд 14Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Справочные материалы
Изучи самостоятельно:
Вероятность события;
Теоремы сложения и
умножения вероятностей;
Формулы полной вероятности, Байеса, Бернулли, Пуасонна.
Основные виды задач
Проверь себя
Реши
самостоятельноРебусы
«Теория вероятностей»
(нажми на фишки, перейдешь на образовательный ресурс Интернета)
Слайд 15Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Ребусы
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Слайд 16Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Проверь себя:
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Что такое
комбинаторика?
В чем состоит комбинаторное правило умножения?
Что такое перестановки?
Записать формулу для
нахождения числа перестановок.Что такое факториал?
Что такое размещения?
Записать формулу для нахождения числа размещений.
Что такое сочетания?
Записать формулу для нахождения числа сочетаний.
В чем различия между перестановками, размещениями и сочетаниями?
Слайд 17Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Основные виды задач
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Вид
1.
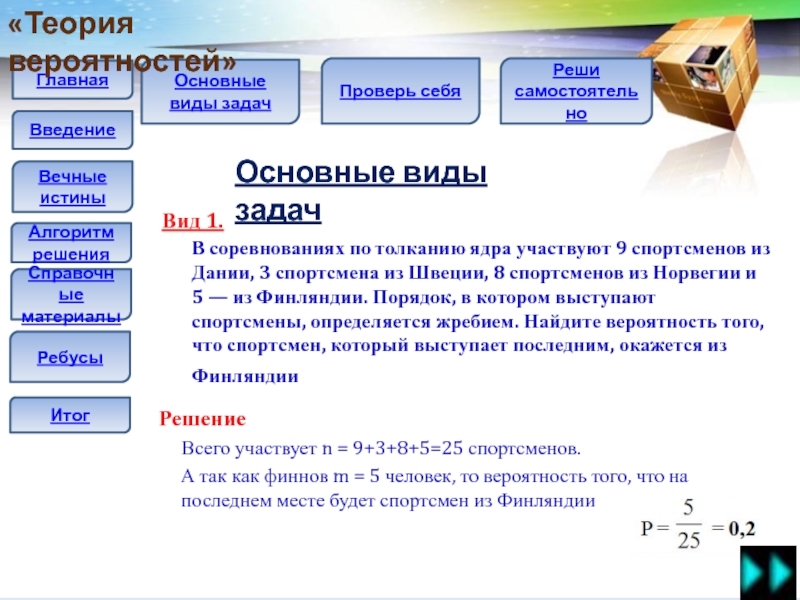
В соревнованиях по толканию ядра участвуют 9
спортсменов из Дании, 3 спортсмена из Швеции, 8 спортсменов из Норвегии и 5 — из Финляндии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Финляндии Решение
Всего участвует n = 9+3+8+5=25 спортсменов.
А так как финнов m = 5 человек, то вероятность того, что на последнем месте будет спортсмен из Финляндии
«Теория вероятностей»
Слайд 18Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Основные виды задач
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Вид
2.
Фабрика выпускает сумки. В среднем на 180
сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. Решение
m = 180-8 = 172 сумки качественные,
n= 180 всего сумок
P = = 0,955...≈ 0,96
«Теория вероятностей»
Слайд 19Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Основные виды задач
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Вид
3.
В случайном эксперименте бросают две игральные кости.
Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.Решение Игральные кости - это кубики с 6 гранями. На первом кубике может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждому варианту выпадения очков соответствует 6 вариантов выпадения очков на втором кубике. Т.е. n = 6×6 = 36. Варианты (исходы эксперимента) будут такие:
1;1 1;2 1;3 1;4 1;5 1;6
2;1 2;2 2;3 2;4 2;5 2;6 и т.д. ..............................
6;1 6;2 6;3 6;4 6;5 6;6
Подсчитаем количество исходов (вариантов), в которых сумма очков двух кубиков равна 8: 2;6 3;5; 4;4 5;3 6;2 Всего m = 5 вариантов. Найдем вероятность.
P = = 0,138 ≈ 0,14
«Теория вероятностей»
Слайд 20Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Основные виды задач
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Вид
4.
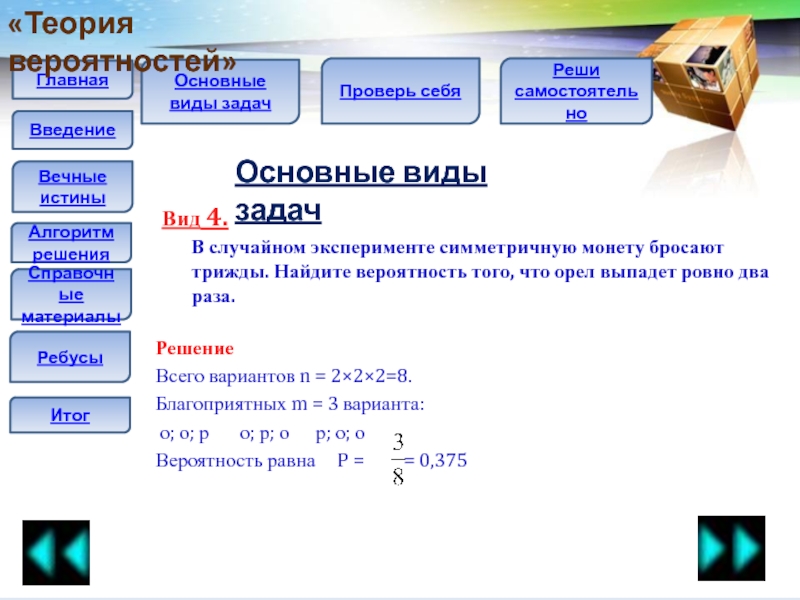
В случайном эксперименте симметричную монету бросают трижды.
Найдите вероятность того, что орел выпадет ровно два раза.Решение
Всего вариантов n = 2×2×2=8.
Благоприятных m = 3 варианта:
о; о; р о; р; о р; о; о
Вероятность равна P = = 0,375
«Теория вероятностей»
Слайд 21Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Основные виды задач
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Вид
5.
В сборнике билетов по биологии всего 35
билетов, в 14 из них встречается вопрос по зоологии. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по зоологии.
Решение
m = 35-14=21- билет без зоологии
n = 35 – всего билетов
Вероятность равна P = =0,6
«Теория вероятностей»
Слайд 22Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Основные виды задач
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Вид
6.
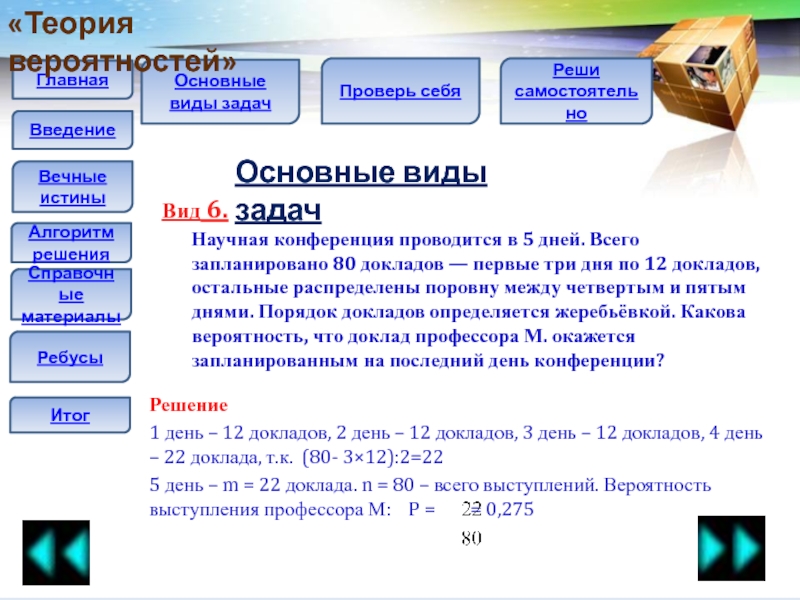
Научная конференция проводится в 5 дней. Всего
запланировано 80 докладов — первые три дня по 12 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение
1 день – 12 докладов, 2 день – 12 докладов, 3 день – 12 докладов, 4 день – 22 доклада, т.к. (80- 3×12):2=22
5 день – m = 22 доклада. n = 80 – всего выступлений. Вероятность выступления профессора М: P = = 0,275
«Теория вероятностей»
Слайд 23Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Основные виды задач
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Вид
7.
В среднем из 2000 садовых насосов,
поступивших в продажу, 12 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение
m = 2000-12=1988 - насосов не подтекает
n = 2000 – всего насосов
Вероятность, что случайно выбранный насос не подтекает:
P = =0,994
«Теория вероятностей»
Слайд 24Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Основные виды задач
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Вид
8.
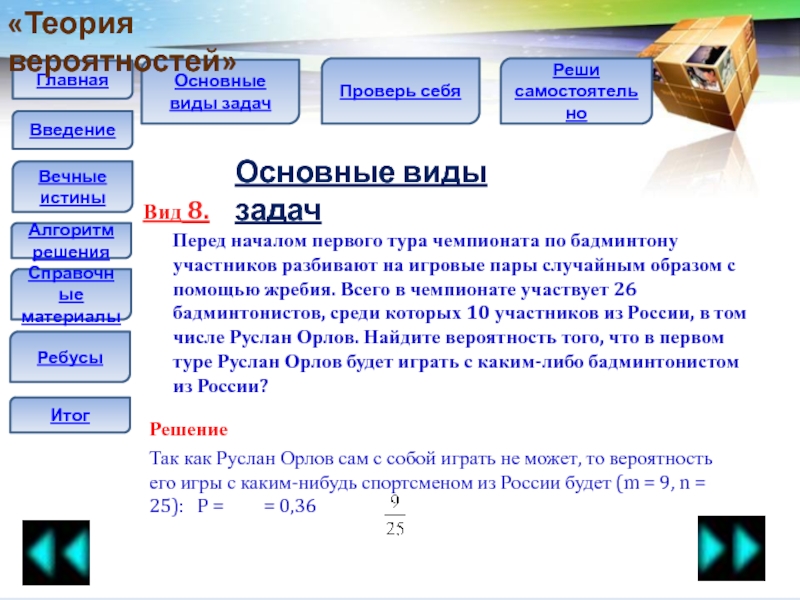
Перед началом первого тура чемпионата по бадминтону
участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
Решение
Так как Руслан Орлов сам с собой играть не может, то вероятность его игры с каким-нибудь спортсменом из России будет (m = 9, n = 25): P = = 0,36
«Теория вероятностей»
Слайд 25Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Основные виды задач
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Вид
9.
Вероятность того, что шариковая ручка пишет
плохо (или не пишет) равна 0,1. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что ручка пишет хорошо.Решение
«Теория вероятностей»
A={ручка пишет хорошо}
Противоположное событие:
Слайд 26Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Основные виды задач
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Вид
10.
На экзамене по геометрии школьнику достается
один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.Решение
«Теория вероятностей»
А={вопрос на тему «Вписанная окружность»}
B={вопрос на тему «Параллелограмм»}
События А и В несовместимы, т.к. нет вопросов относящихся к двум
темам одновременно.
С={вопрос по одной из этих тем}
Р(С)=Р(А) + Р(В) Р(С)=0,2 + 0,15=0,35
Слайд 27Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Основные виды задач
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
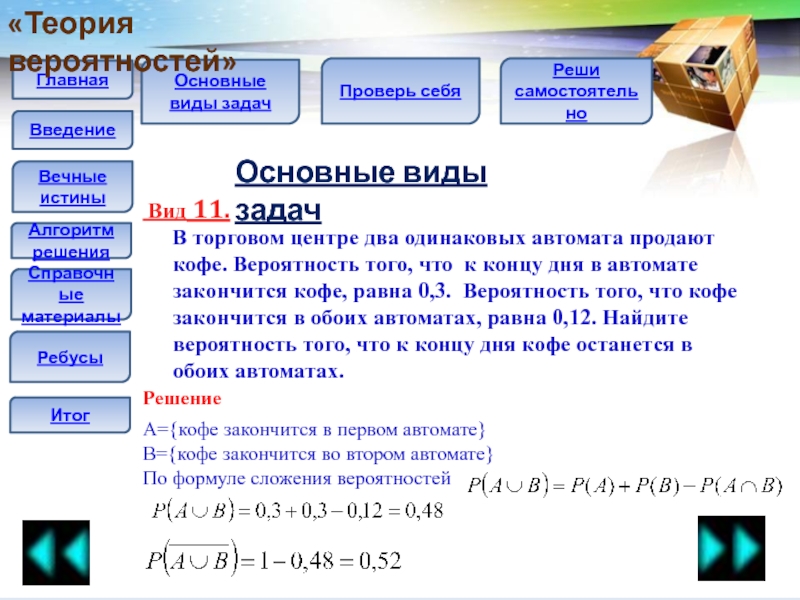
Вид 11.
В торговом центре два одинаковых автомата
продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.Решение
«Теория вероятностей»
А={кофе закончится в первом автомате}
B={кофе закончится во втором автомате}
По формуле сложения вероятностей
Слайд 28Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Итог
Основные виды задач
Основные виды задач
Проверь себя
Реши самостоятельно
Ребусы
Вид 12.
Биатлонист пять раз стреляет по мишеням.
Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых.Решение
«Теория вероятностей»
Вероятность попадания = 0,8
Вероятность промаха = 1 - 0,8 = 0,2
По формуле умножения вероятностей Р(А)= 0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2
Р(А)= 0,512 ∙ 0,04 = 0,02048 ≈ 0,02
Слайд 29Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Классическое определение вероятности
Сложение и умножение вероятностей
Случайные события
Комбинаторика
На
удачу
Реши самостоятельно:
Основные виды задач
Итог
Проверь себя
Реши самостоятельно
Ребусы
«Теория вероятностей»
Слайд 30Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Классическое определение вероятности:
Задача № 1 Брошена игральная
кость. Какова вероятность того, что выпадет четное число очков?
Задача №
2 В 2-х коробках лежат карандаши одинаковой величины и формы, но разного цвета. В первой коробке 4 красных и 6 черных, а второй 3 красных, 5 синий и 2 черных. Из обеих коробок вынимается наугад по одному карандашу. Какова вероятность того, что ода карандаша окажутся красными?Задача № 3 На тарелке 15 пирожков: 6 с яблоками, 4 с капустой и 5 с печенью. Варя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с яблоками.
Задача № 4 При двукратном бросании игрального кубика в сумме выпало 6 очков. Найти вероятность того, что первый раз выпало меньше трех очков.
Задача № 5 Витя наудачу выбирает двузначное число. Найдите вероятность того, что оно начинается на 9.
Задача № 6 Двое играют в кости – они по разу бросают игральный кубик. Выигрывает тот, у кого больше очков. Если выпадает поровну – ничья. Первый бросил кубик и у него выпало 4 очка. Найдите вероятность того, что он выиграет.
Основные виды задач
Итог
Проверь себя
Реши самостоятельно
Ребусы
«Теория вероятностей»
Слайд 31Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Сложение и умножение верятностей:
Задача № 1 Биатлонист
5 раз стреляет по мишеням. Вероятность попадания в мишень при
одном выстреле равна 0,7. Найдите вероятность того, что биатлонист первые 4 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.Задача № 2 В магазине стоят три платежных автомата. Каждый из них может быть неисправен с вероятностью 0,1. Найдите вероятность того, что хотя бы один автомат исправен.
Задача № 3 В классе 21 ученик, среди них два друга – Тоша и Гоша. На уроке физкультуры класс случайным образом разбивают на три равные группы. Найдите вероятность того, что Тоша и Гоша попали в одну группу.
Задача № 4 В случайном эксперименте монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
Задача № 5 В корзине лежат 9 черных шаров и 7 красных. Мальчик достает 2 шара одинакового цвета. Сколькими способами он может это сделать?
Задача № 6 В группе из 20 студентов, среди которых 2 отличника, надо выбрать 4 человека для участи в конференции. Сколькими способами можно выбрать этих четверых , если отличники обязательно должны попасть на конференцию?
Основные виды задач
Итог
Проверь себя
Реши самостоятельно
Ребусы
«Теория вероятностей»
Слайд 32Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Ребусы
Случайные события:
Задача № 1 В партии из
20 изделий 5 изделий имеют скрытый дефект. Какова вероятность того,
что из взятых наугад 4 изделий 2 изделия являются дефектными?Задача № 2 На склад с трех предприятий поступает продукция 1 и 2 сорта. В продукции 1 предприятия содержится 15% второсортных изделий, в продукции второго предприятия – 25%, в продукции третьего предприятия – 30%. Чему равна вероятность того, что среди трех изделий (по одному из продукции каждого предприятия) окажутся первосортными два изделия.
Задача № 3 В цехе работают три станка. Вероятность отказа в течении смены для станков соответственно равна 0,1; 0,2 и 0,15. Найти вероятность того, что в течение смены безотказно проработают два станка.
Задача № 4 В урне 4 белых и 6 черных шаров. Из урны на удачу извлечены 2 шара. Найти вероятность того, что они разного цвета.
Задача № 5 Найти вероятность наступления события А ровно 3 раза в 5 независимых испытаниях, если вероятность проявления этого события в каждом испытании равна 1/3.
Задача № 6 Какова вероятность того, что пятизначное число состоит из цифр 0, 1, 2, 3, 4.
Основные виды задач
Итог
Проверь себя
Реши самостоятельно
«Теория вероятностей»
Слайд 33Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Ребусы
Комбинаторика:
Задача № 1 Из 9 учеников, жеребьевкой
выбирают группу болельщиков, состоящих из 6 человек (разыгрывают 6 билетов
на бобслей). Сколько всего существуют различных вариантов состава такой группы болельщиков?Задача № 2 На окружности выбрано 12 точек. Сколько хорд можно провести с концами в этих точках?
Задача № 3 Три девочки и 4 мальчика рассаживаются в ряд на 7 подряд
расположенных мест, причем девочки садятся на первые три места, а мальчики на остальные. Сколькими различными способами они могут это сделать?
Задача № 4 Два ученика одновременно загадывают и называют по одному целому числу от 1 до 5 включительно. Найти вероятность того, что сумма названных чисел будет меньше 5?
Задача № 5 Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найти вероятность того, что биатлонист хотя бы один раз попадет в мишени.
Задача № 6 Вероятность того, что новая кофемолка прослужит больше года, равна 0,93. Вероятность того, что она прослужит больше двух лет, равна 0,81. Найти вероятность того, что кофемолка прослужит меньше двух лет, но больше года.
Основные виды задач
Итог
Проверь себя
Реши самостоятельно
«Теория вероятностей»
Слайд 34Главная
Введение
Вечные истины
Алгоритм решения
Справочные материалы
Ребусы
«На удачу»:
Задача № 1 Какое событие называется
невозможным? Приведите 3 примера невозможных событий.
Задача № 2 Галя дважды
бросает игральный кубик. В сумме у неё выпало 9 очков. Найдите вероятность того, что при втором броске выпало 6 очков.Задача № 3 Телевизор у Любы сломался и показывает только один случайный канал. Люба включает телевизор. В это время по двадцати пяти каналам из пятидесяти показывают кинокомедии. Найдите вероятность того, что Люба попадет на канал, где комедия не идет.
Задача № 4 Коля наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 6.
Задача № 5 Два игральных кубика бросают одновременно и в сумме получают 4 очка. Какова вероятность, что на каждом кубике выпало по два очка?
Задача № 6 В чемпионате мира участвуют 15 команд. С помощью жребия их нужно разделить на пять групп по три команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5.
Капитаны команд тянут по одной карточке. Какова вероятность того,
что команда из России окажется в пятой группе?
Проверь себя
Основные виды задач
Реши самостоятельно
Итог
«Теория вероятностей»