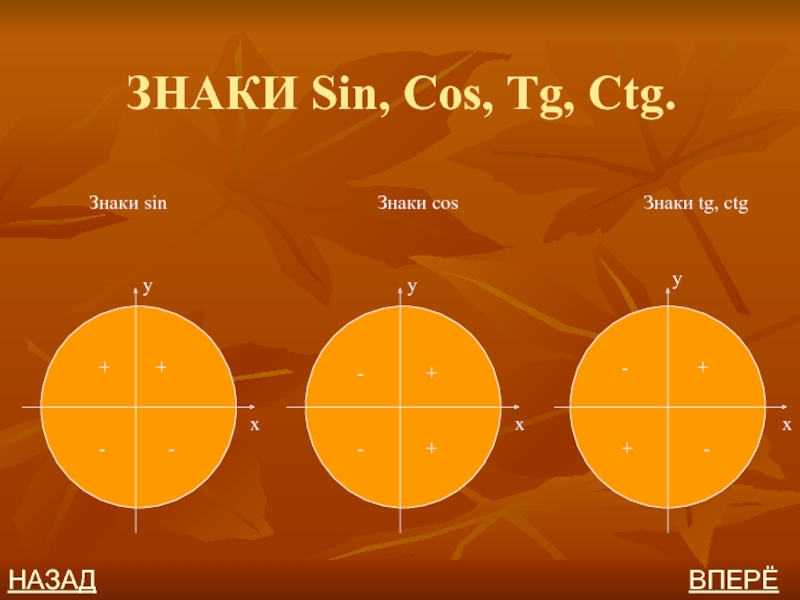
R.
Косинусом угла α называется отношение абсциссы точки В к R.
Тангенсом
угла α называется отношение ординаты точки В к ее абсциссе.Котангенсом угла α называется отношение абсциссы точки В к ее ординате.
α
R
B (x;y)
НАЗАД
y
x
ВПЕРЁД