Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Все о треугольниках
Содержание
- 1. Все о треугольниках
- 2. Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, последовательно соединенных отрезками
- 3. Виды треугольников: остроугольныеТупоугольныепрямоугольные
- 4. Равнобедренный треугольник – треугольник, у
- 5. Если два треугольника равны, то элементы одного
- 6. Первый признак равенства треугольников: Если две стороны
- 7. Второй признак равенства треугольников: Если сторона и
- 8. Третий признак равенства треугольников: Если три стороны
- 9. Медиана -отрезок, соединяющийвершину треугольникас серединой противоположнойстороныАВСДВД = ДС, АД – медиана
- 10. Биссектриса -отрезок биссектрисыугла треугольника,соединяющий вершинутреугольника с точкойпротивоположнойстороныАВКС
- 11. Высота -перпендикуляр,проведенный извершины треугольникак прямой, содержащейпротивоположнуюсторонуАДСВВД АС, ВД - высота
- 12. В любом треугольнике медианы пересекаются
- 13. В равнобедренном треугольникебиссектриса, проведенная к основанию, является медианойи высотой
- 14. Внешним углом треугольника называется угол, смежный с
- 15. Прямоугольный треугольниккатет к а т е тгипотенуза
- 16. Некоторые свойства прямоугольных треугольников сумма двух острых
- 17. Признаки равенства прямоугольных треугольников Если катеты одного
- 18. Признаки равенства прямоугольных треугольников если гипотенуза и
- 19. Соотношение между сторонами и углами треугольника В
- 20. Неравенство треугольникаКаждая сторона треугольника меньше суммы двух
- 21. Построение треугольника по трем сторонам•••CBA
- 22. Построение треугольника по двум сторонам и углу между ними•••ABCa
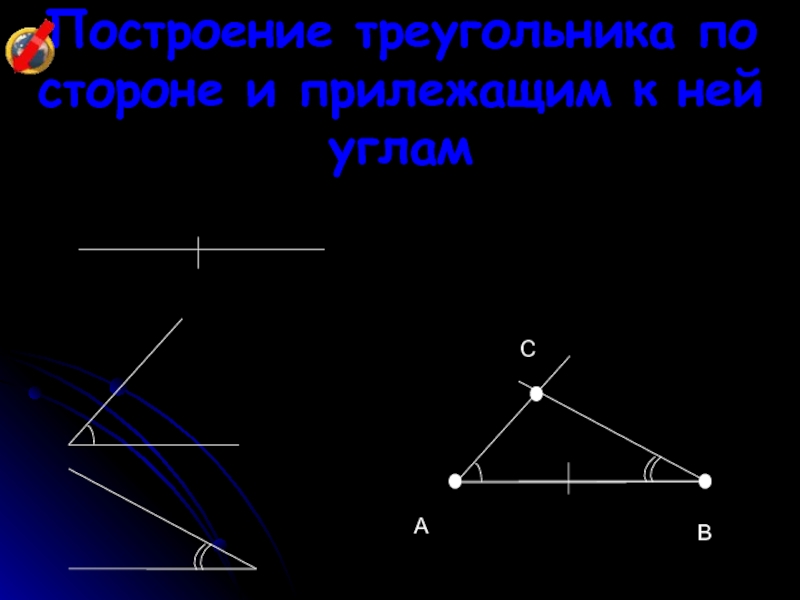
- 23. Построение треугольника по стороне и прилежащим к ней угламABC
- 24. Докажите, что треугольник АОД равен треугольнику СОВ
- 25. Докажите, что треугольник АВД равен треугольнику СДВ
- 26. Докажите, что треугольник АВД равен треугольнику СДВ
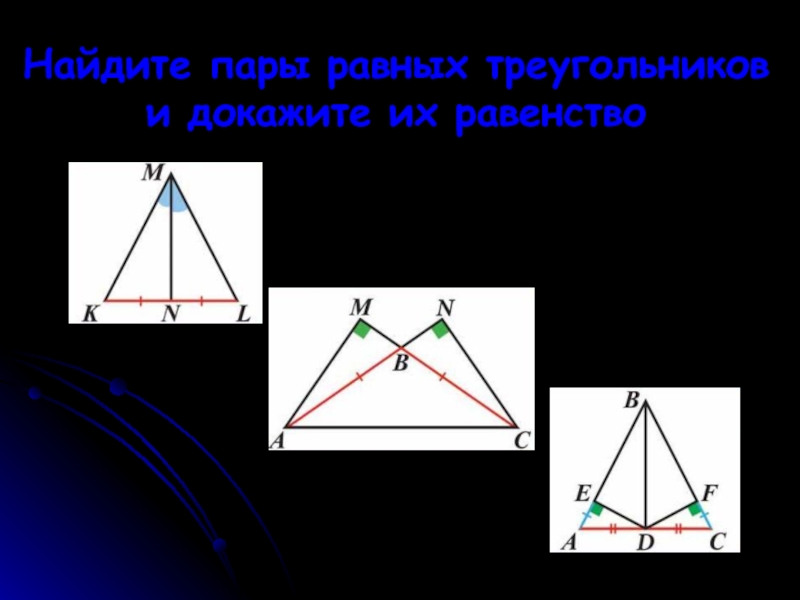
- 27. Найдите пары равных треугольников и докажите их равенство
- 28. Скачать презентанцию
Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, последовательно соединенных отрезками
Слайды и текст этой презентации
Слайд 1Все о треугольниках
ГЕОМЕТРИЯ
7 КЛАСС
Составила: учитель математики ОГКУЗ «Детский санаторий
г. Грайворон»
Слайд 2Треугольник –
геометрическая фигура,
состоящая из трех точек,
не лежащих
на одной
прямой, последовательно
соединенных отрезками
Слайд 5Если два треугольника
равны, то элементы одного
треугольника соответственно равны
элементам другого треугольника.
В равных треугольниках против соответственно равных сторон
лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.
Слайд 6Первый признак равенства треугольников:
Если две стороны и угол между
ними одного треугольника соответственно равны двум сторонам и углу между
ними другого треугольника, то такие треугольники равны.
Слайд 7Второй признак равенства треугольников:
Если сторона и два прилежащих к
ней угла одного треугольника соответственно равны стороне и двум прилежащим
к ней углам другого треугольника, то такие треугольники равны.
Слайд 8Третий признак равенства треугольников:
Если три стороны одного треугольника соответственно
равны трем сторонам другого треугольника, то такие треугольники равны.
Слайд 9
Медиана -
отрезок, соединяющий
вершину треугольника
с серединой
противоположной
стороны
А
В
С
Д
ВД = ДС, АД –
медиана
Слайд 10Биссектриса -
отрезок биссектрисы
угла треугольника,
соединяющий вершину
треугольника с точкой
противоположной
стороны
А
В
К
С
ВАК
= САК,
АК - биссектриса
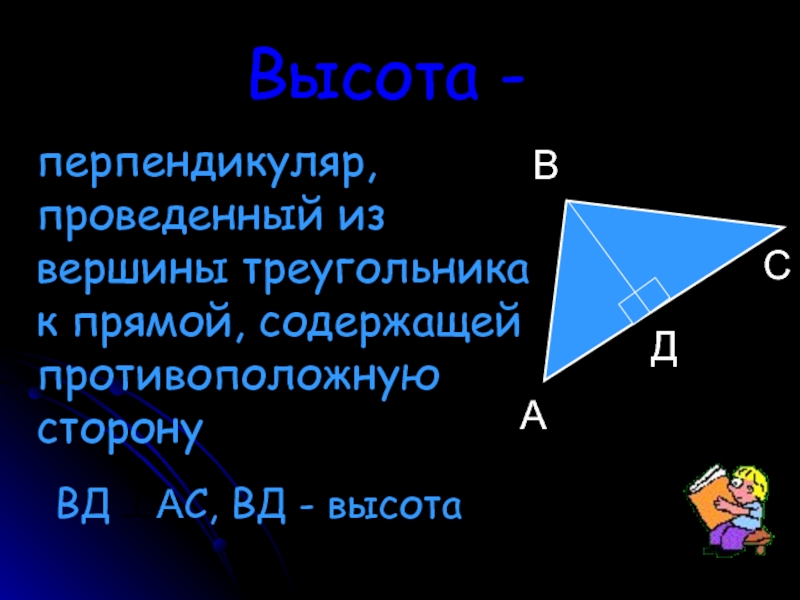
Слайд 11Высота -
перпендикуляр,
проведенный из
вершины треугольника
к прямой, содержащей
противоположную
сторону
А
Д
С
В
ВД АС, ВД -
высота
Слайд 12В любом треугольнике
медианы
пересекаются в одной точке,
биссектрисы пересекаются в
одной точке, высоты или их
продолжения также
пересекаются
в одной точке
Слайд 13В равнобедренном треугольнике
биссектриса, проведенная к
основанию, является
медианой
и высотой
Слайд 14Внешним углом треугольника называется угол, смежный с каким – нибудь
углом этого треугольника
Внешний
Угол
Внешний угол треугольника равен сумме двух других
углов треугольника, не смежных с ним
Слайд 16Некоторые свойства прямоугольных треугольников
сумма двух острых углов прямо-
угольного треугольника равна 90°
катет прямоугольного треуголь -
ника,
лежащий против угла в 30°, равен половине гипотенузы
если катет прямоугольного треугольника
равен половине гипотенузы, то угол,
лежащий против этого катета, равен 30°
30о
Слайд 17Признаки равенства
прямоугольных треугольников
Если катеты одного прямоугольного
треугольника соответственно
равны
катетам другого, то такие треугольники
равны
Если катет и прилежащий к нему острыйугол одного прямоугольного треугольника
соответственно равны катету и прилежащему
к нему острому углу другого, то такие
треугольники равны
Слайд 18Признаки равенства
прямоугольных треугольников
если гипотенуза и острый угол одного
прямоугольного треугольника
соответственно равны гипотенузе и острому
углу другого, то такие треугольники равны если гипотенуза и катет одного
прямоугольного треугольника
соответственно равны гипотенузе и катету
другого, то такие треугольники равны
Слайд 19Соотношение между сторонами
и углами треугольника
В треугольнике: 1) против большей
стороны лежит больший угол;
2) обратно, против большего угла
лежит большая сторона В прямоугольном треугольнике
гипотенуза больше катета
Если два угла треугольника равны, то
треугольник равнобедренный
Слайд 20Неравенство треугольника
Каждая сторона треугольника меньше суммы двух других сторон
Для любых
трех точек А, В и С, не лежащих на одной
прямой, справедливы неравенства:АВ < AC + CB
AC < AB + BC
BC < BA + AC
Теги
