Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сравнение и измерение отрезков 7 класс
Содержание
- 1. Сравнение и измерение отрезков 7 класс
- 2. Основные геометрические фигуры:aA
- 3. АКСИОМЫА1. Каждой прямой принадлежат по крайней мере
- 4. Тема:Сравнение и измерение отрезков
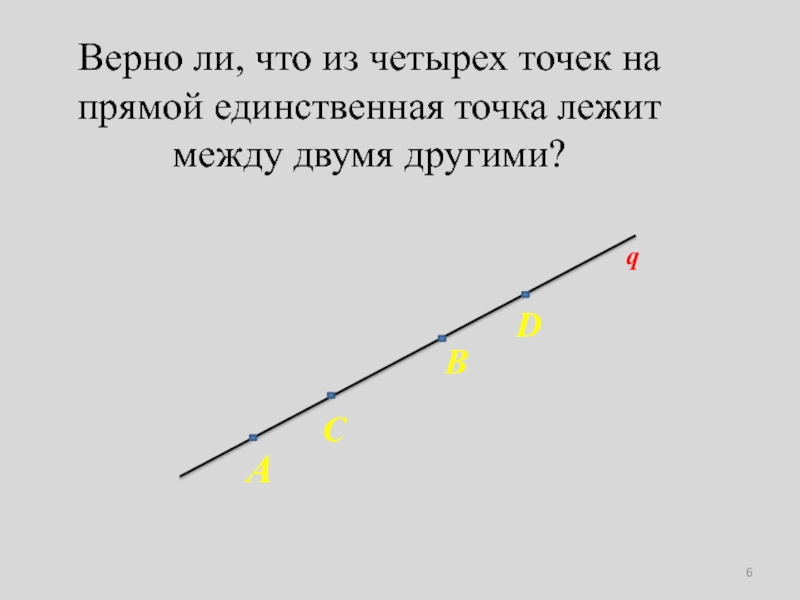
- 5. Аксиома 4Из трех точек на прямой единственная
- 6. Верно ли, что из четырех точек на прямой единственная точка лежит между двумя другими?qADCB
- 7. Отрезок - это геометрическая фигура, состоящая из
- 8. Верно ли, что
- 9. КОНТРПРИМЕР!АВ
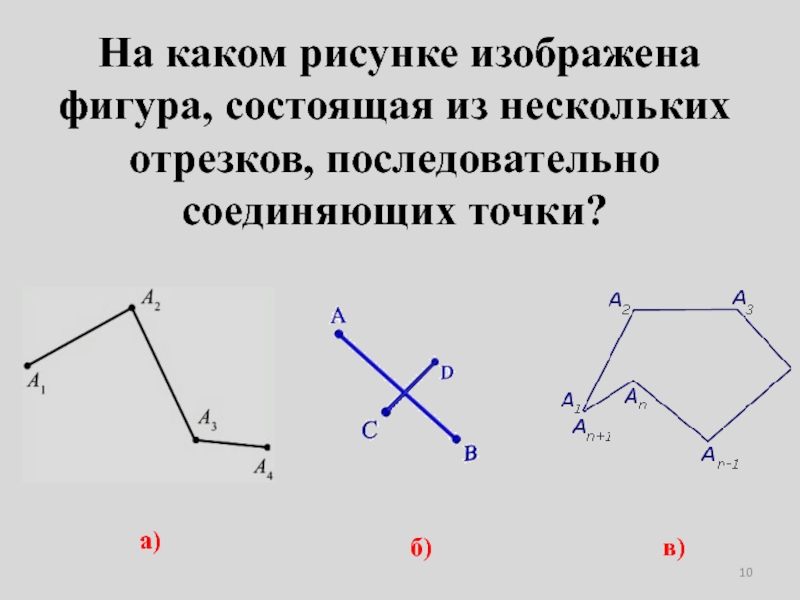
- 10. На каком рисунке изображена фигура, состоящая из нескольких отрезков, последовательно соединяющих точки? а)б)в)
- 11. Ломаная – это геометрическая фигура, состоящая из
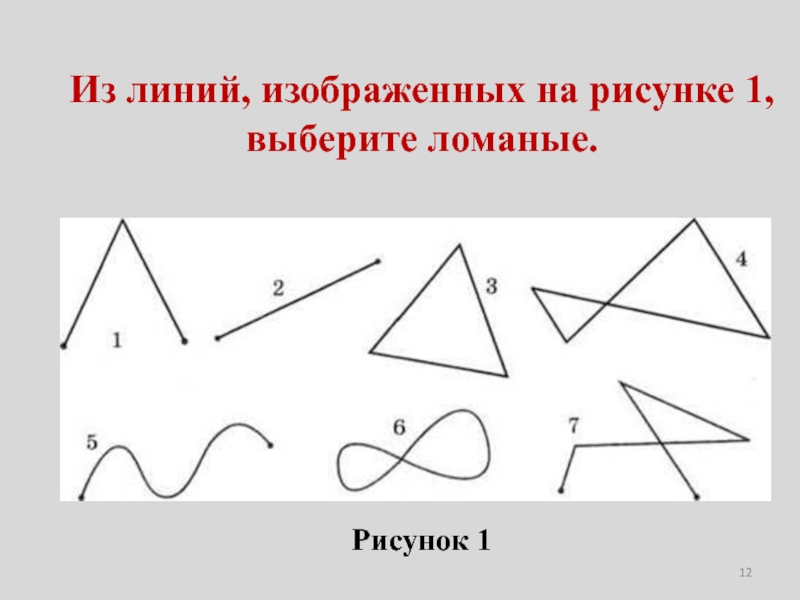
- 12. Рисунок 1Из линий, изображенных на рисунке 1, выберите ломаные.
- 13. Назовите точки, лежащие по одну сторону от точки А.аPTAF
- 14. Луч - геометрическая фигура, состоящая из точки
- 15. Луч АВАВЛуч ВА
- 16. Назовите лучи прямой PT с началом в
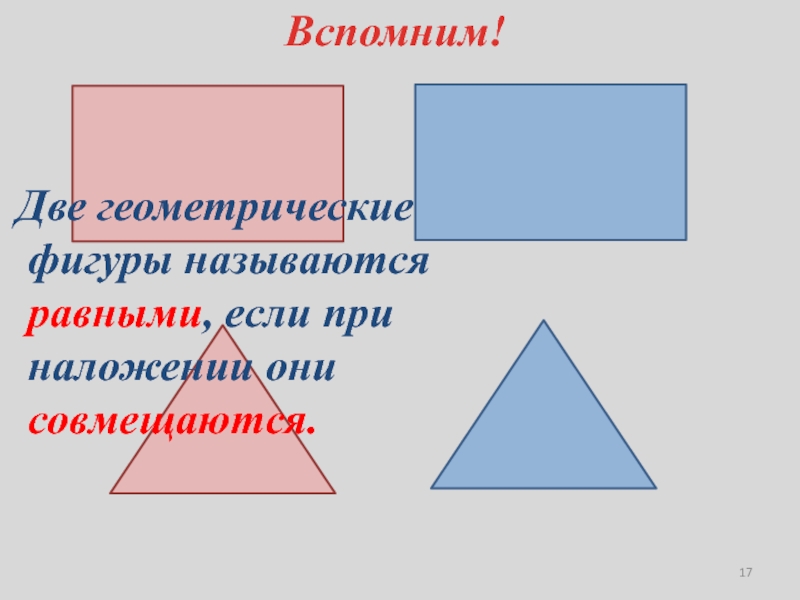
- 17. Вспомним!Две геометрические фигуры называются равными, если при наложении они совмещаются.
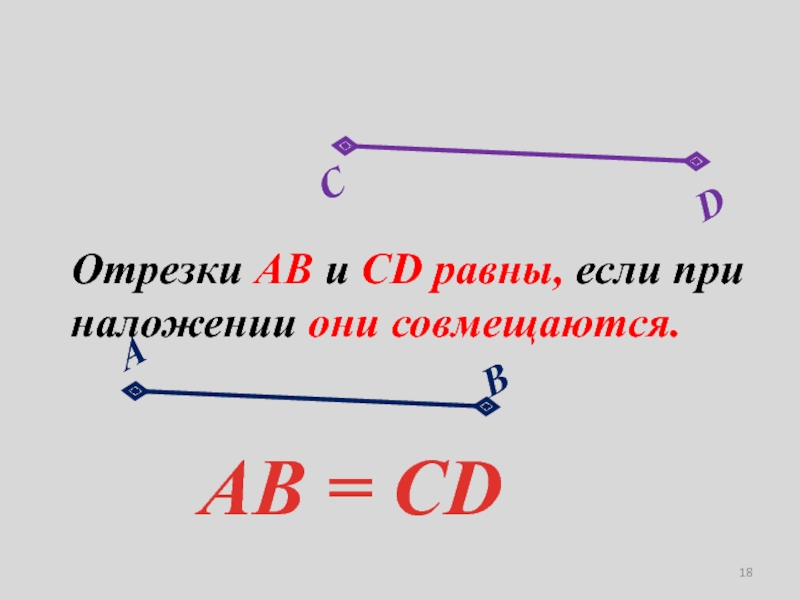
- 18. Отрезки АВ и СD равны, если при наложении они совмещаются.АВ = СD
- 19. Если концы отрезков не совпадают то отрезки АВ и СD не равны.
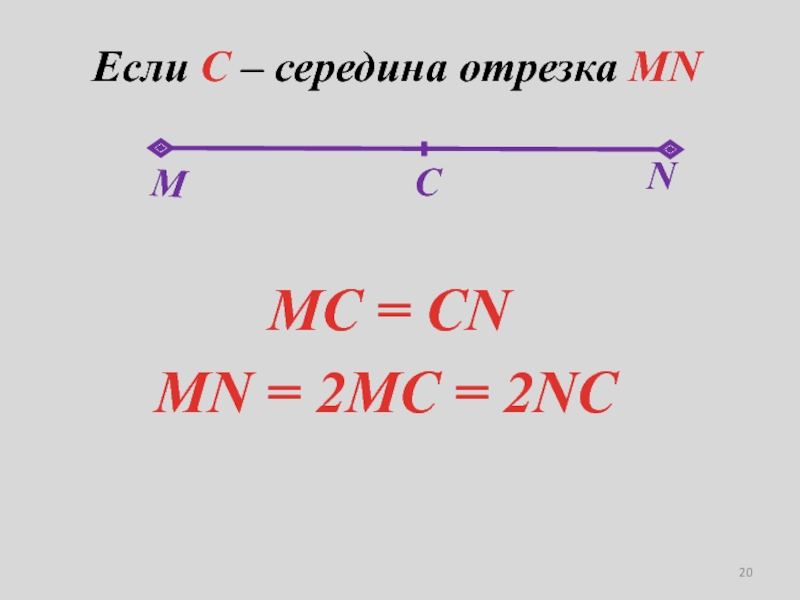
- 20. Если С – середина отрезка MNMC = СN MN = 2MC = 2NC
- 21. Аксиома откладывания отрезкаНа любом луче от его начала можно отложить единственный отрезок, равный данному.
- 22. АВОЕ = 1 смАВ = 5 смОЕ
- 23. СВОЙСТВА ДЛИНЫ ОТРЕЗКОВ
- 24. 1. При выбранной единице измерения каждый отрезок имеет длину, которая больше нуля.
- 25. 2. При выбранной единице измерения для любого положительного числа существует отрезок, длина которого выражается этим числом.
- 26. 3. Равные отрезки имеют равные длины
- 27. 4. Отрезки, имеющие равные длины, равны.
- 28. 5. Длина отрезка равна сумме длин отрезков,
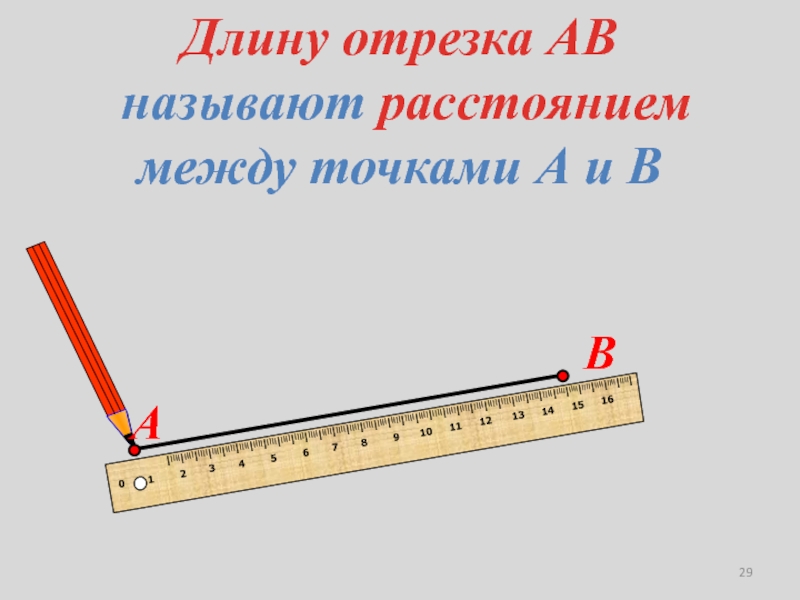
- 29. Длину отрезка АВ называют расстоянием между точками А и В
- 30. РЕШЕНИЕ ЗАДАЧ
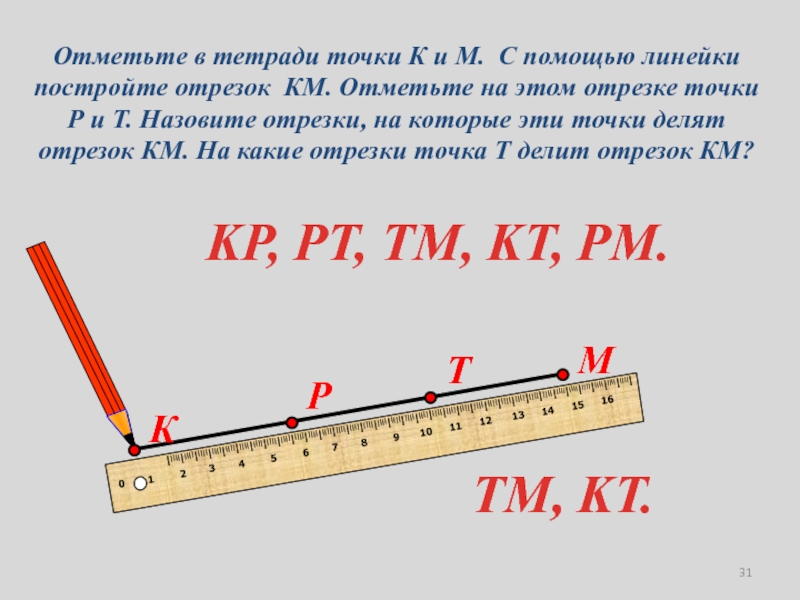
- 31. Отметьте в тетради точки К и М.
- 32. В АС, АВ = 3,7
- 33. ОПОРНАЯ ЗАДАЧА!!!
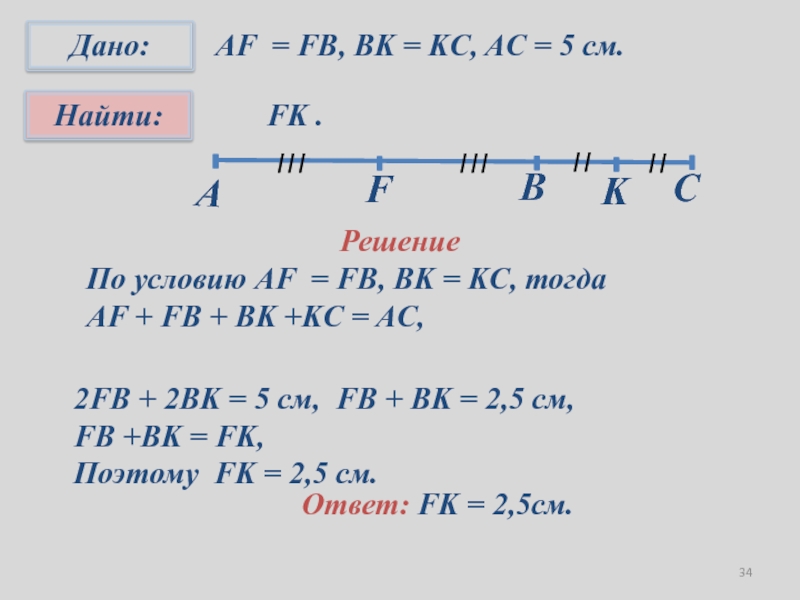
- 34. AF = FB, BK = KC,
- 35. А, О, В – лежат на одной
- 36. б) если точка О не лежит на
- 37. Ответить на вопросы:Какая геометрическая фигура называется отрезком?Какая
- 38. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3АКСИОМЫ
А1. Каждой прямой принадлежат по крайней мере две точки.
А2. Существует
по крайней мере три точки, не принадлежащие одной прямой.
две точки плоскости проходит единственная прямая, каждая точка которой принадлежит плоскости.Слайд 5Аксиома 4
Из трех точек на прямой единственная точка лежит между
двумя другими.
q
A
B
C
C лежит между A и B
Слайд 7Отрезок - это геометрическая фигура, состоящая из двух точек прямой
и всех ее точек, лежащих между данными точками
A и
D – концы отрезка.С и В – внутренние точки
q
A
D
C
B
Слайд 8 Верно ли, что отрезком называется геометрическая фигура, состоящая из двух
точек и всех точек, лежащих между данными точками?
Слайд 10 На каком рисунке изображена фигура, состоящая из нескольких отрезков,
последовательно соединяющих точки?
а)
б)
в)
Слайд 11Ломаная – это геометрическая фигура, состоящая из отрезков А1A2, А2А3,
… , Аn-1An , последовательно соединяющих точки А1, A2, А3,
… , Аn-1 , An.Точки А1, A2, А3, … , Аn-1 , An. - вершины ломаной
Отрезки А1A2, А2А3, … , Аn-1An - звенья ломаной
Слайд 14Луч - геометрическая фигура, состоящая из точки прямой и всех
ее точек, лежащих по одну сторону от данной точки
Данная точка
называется началом луча.Слайд 16Назовите лучи прямой PT с началом в точке F.
а
P
T
A
F
Противоположные лучи
– это различные лучи одной прямой, имеющие общее начало.
FT и
FPСлайд 21Аксиома откладывания отрезка
На любом луче от его начала можно отложить
единственный отрезок, равный данному.
Слайд 22А
В
ОЕ = 1 см
АВ = 5 см
ОЕ – единичный отрезок
Длина
отрезка - геометрическая величина, которая показывает, сколько раз единица измерения
и ее части укладываются в измеряемом отрезке.Длина обозначается: АВ
Слайд 252. При выбранной единице измерения для любого положительного числа существует
отрезок, длина которого выражается этим числом.
Слайд 31Отметьте в тетради точки К и М. С помощью линейки
постройте отрезок КМ. Отметьте на этом отрезке точки Р и
Т. Назовите отрезки, на которые эти точки делят отрезок КМ. На какие отрезки точка Т делит отрезок КМ?KP, PT, TM, KT, PM.
TM, KT.
Слайд 32 В АС, АВ = 3,7 см, АС =
7,2 см
ВС .
Решение
?
Так как В АС, АВ +
ВС = АС,ВС = АС - АВ
ВС = 7,2 – 3,7 = 3,5 (см).
Ответ: BС = 3,5см.
Слайд 34 AF = FB, BK = KC, AC = 5
см.
FK .
Решение
2FB + 2BK = 5 см, FB + BK
= 2,5 см,FB +BK = FK,
Поэтому FK = 2,5 см.
Ответ: FK = 2,5см.
По условию AF = FB, BK = KC, тогда
AF + FB + BK +KC = AC,
Слайд 35А, О, В – лежат на одной прямой,
ОА = 12
см, ОВ = 9 см.
расстояние между серединами
отрезков
ОА и ОВ - ?Решение
Пусть М – середина отрезка ОА, N – середина отрезка ОВ.
Возможны два случая:
а) если точка О лежит на отрезке АВ, то МО = АО : 2 = 6 см,
NO = BO : 2 = 4,5 см.
Расстояние между серединами отрезков ОА и ОВ равно
длине отрезка MN, a MN = MO + NO = 6 + 4,5 = 10,5 (см)
Слайд 36б) если точка О не лежит на отрезке АВ
б) если
точка О не лежит на отрезке АВ, то МО =
АО : 2 = 6 см,NO = BO : 2 = 4,5 см.
Пусть по условию: М – середина отрезка ОА, N – середина отрезка ОВ.
Решение
MN = MO – ON = 6 – 4,5 = 1,5 (см).
Ответ: а) 10,5 см; б) 1,5 см.
Слайд 37Ответить на вопросы:
Какая геометрическая фигура называется отрезком?
Какая фигура называется ломаной?
Какие
виды ломаной вы знаете?
Какая геометрическая фигура называется лучом?
Сформулируйте аксиому откладывания
отрезка.Что такое длина отрезка?