Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Арифметический корень степени n"
Содержание
- 1. "Арифметический корень степени n"
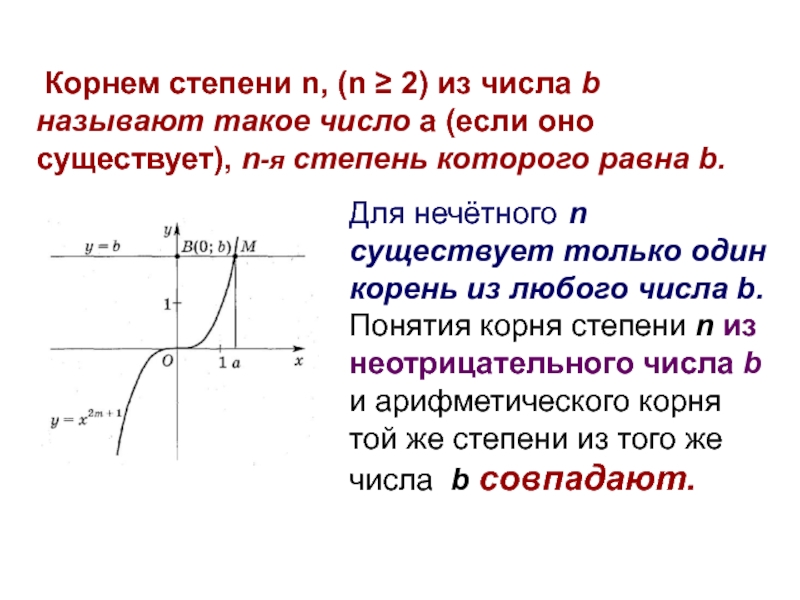
- 2. Корнем степени n, (n ≥ 2)
- 3. Корнем степени n, (n ≥ 2)
- 4. Утверждения1. Если b — неотрицательное число, а
- 5. Пример 1.а) Записи - это записи арифметических
- 6. УтверждениеНапример:
- 7. Теорема 1. Для натурального числа n (n ≥ 2) и неотрицательного числа а справедливы равенства
- 8. Теорема 1. Доказательство.Т. к. а – неотрицательной
- 9. Теорема 1. Доказательство.Т. к. а – неотрицательной
- 10. Пример 2.
- 11. Теорема 2. Для натурального числа n (n
- 12. Теорема 3. Для натурального числа n (n
- 13. Теорема 3. Доказательство.Из равенства
- 14. Пример 3.
- 15. Замечание. 1). Если n – нечётное число,
- 16. Пример 4.
- 17. Вынесение множителя из под знака корня.Пример 5.
- 18. Вопросы1.Что называют корнем степени n, (n ≥
- 19. Вопросы3. Для каких чисел а Є R
- 20. Вопросы5. Чему равен корень степени n, (n
- 21. Вопросы7. Является ли записьюарифметического корня выражение ?нетнетданетда
- 22. Верны ли утвержденияНет2). Если аn ≥ b
- 23. Вычислите
- 24. Ответы
- 25. ЛитератураУчебник для 10 класса общеобразовательных учреждений.
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2 Корнем степени n, (n ≥ 2) из числа b
называют такое число a (если оно существует), n-я степень которого
равна b.Для нечётного n существует только один корень из любого числа b. Понятия корня степени n из неотрицательного числа b и арифметического корня той же степени из того же числа b совпадают.
Слайд 3 Корнем степени n, (n ≥ 2) из числа b
называют такое число a (если оно существует), n-я степень которого
равна b.Для чётного n существуют два корня из положительного числа b. Один из них положительный :
это арифметический корень степени n из числа b.
это не арифметический
корень.
Слайд 4Утверждения
1. Если b — неотрицательное число, а n— любое натуральное
число (n ≥ 2), то запись
означает арифметический корень степе ни n из числа b.2. Если b- отрицательное число, а n = 2m+ 1 (m ≥ 1) — нечётное число, то запись означает корень степени 2 m + 1 из числа b, но этот корень не является арифметическим корнем.
3. Если b — отрицательное число, а n = 2m (m ≥ 1)— четное число,
то запись не имеет смысла.
Слайд 5Пример 1.
а) Записи
- это записи арифметических корней.
б) Записи
это записи корней,
не являющихся арифметическими.
в) Записи
- не имеют
смысла. Слайд 8Теорема 1.
Доказательство.
Т. к. а – неотрицательной число, то
есть по определению неотрицательное
число, n-я степень которого есть а.
Это и выражается равенством 1).
Слайд 9Теорема 1.
Доказательство.
Т. к. а – неотрицательной число, то аn
≥ 0
и есть
по определению неотрицательное число, n-я степень которого есть аn. Таким числом является а.Это и выражается равенством 2).
Слайд 11Теорема 2. Для натурального числа n (n ≥ 2) и
неотрицательных чисел а и b из равенства
аn
= bn следует равенство а = b.Доказательство.
Известно, что существует только один корень n-й степени из неотрицательного числа. Поэтому для неотрицательных чисел из их равенства корней n-й степени из них, т. е. из равенства аn = bn следует равенство
Учитывая, что а ≥ 0 и b ≥ 0, и используя
равенство 2)
получаем, что
Следовательно, а = b.
Слайд 12
Теорема 3. Для натурального числа n (n ≥ 2) и
неотрицательных чисел а, b и с (с ≠ 0)
из справедливы равенстваСлайд 13Теорема 3.
Доказательство.
Из равенства
имеем
Правые части полученных равенств
равны. Следовательно, равны и левые их части:Т. к. числа неотрицательны, то, применяя теорему 2, получаем, что справедливо равенство (3).
Аналогично доказывается равенство
Слайд 15Замечание. 1). Если n – нечётное число, то теоремы 1,
2, 3 справедливы для любых действительных чисел а, b и
с (с≠0).2). Для натурального числа m и любого действительного числа а справедливо равенство
потому, что
Слайд 18Вопросы
1.Что называют корнем степени n, (n ≥ 2)
из числа b? Привести примеры.
Корнем степени n, (n ≥
2) из числа b называют такое число a (если оно существует), n-я степень которого равна b.2. Что называют арифметическим корнем степени n, (n ≥ 2) из числа b? Привести примеры.
Неотрицательный корень степени n, (n ≥ 2) из неотрицательного числа b называют арифметическим корнем степени n из числа b.
Слайд 19Вопросы
3. Для каких чисел а Є R введено понятие арифметического
корня степени n, (n ≥ 2) из числа а?
a
≥0.4. Сколько существует арифметических корней степени n, (n ≥ 2) из данного числа?.
Не более одного.
Слайд 20Вопросы
5. Чему равен корень степени n, (n ≥ 2) из
произведения неотрицательных чисел?
Рaвен произведению корней степени n, из
этих чисел.
6.
Чему равен корень степени n, (n ≥ 2) изчастного положительных чисел?
Рaвен частному корней степени n, из
этих чисел.
Слайд 22Верны ли утверждения
Нет
2). Если аn ≥ b n , то
а ≥ b.
Нет
3) Для каких значений а и b
утверждения 1) и 2) будут верными? Для неотрицательных