Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Мир тригонометрии
Содержание
- 1. Мир тригонометрии
- 2. «Великая книга природы может быть прочтена только
- 3. История первая- «Гипатия»
- 4. Мир тригонометрии- основные тригонометрические тождества
- 5. Мир тригонометрии: основные тригонометрические тождестваЦели урока:
- 6. Актуализация опорных знаний:Сформулируйте определение синуса острого угла
- 7. Актуализация опорных знаний:Перевести: в радианы 30°,45°,60°,90,270°,-720° в
- 8. Переход от градусной меры углов к
- 9. Зачем нам нужна тригонометрия
- 10. Тригономе́трия (от греч. τρίγονο (треугольник) и греч.
- 11. Первые тригонометрические таблицы были, вероятно, составлены Гиппархом
- 12. Леонард Эйлер (1707 – 1783)Иоганн Бернулли (1642-1727)
- 13. Разделы тригонометрииТригонометрия делится на плоскую, или прямолинейную,
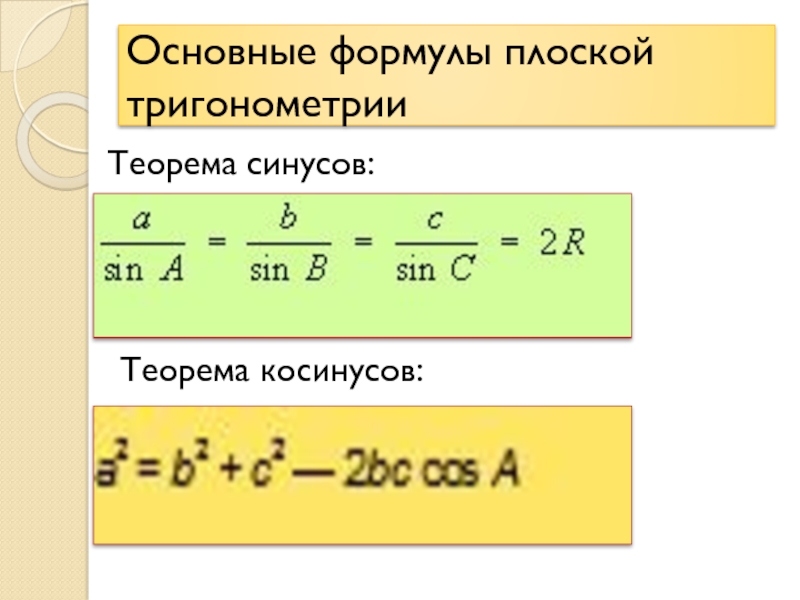
- 14. Основные формулы плоской тригонометрииТеорема синусов:Теорема косинусов:
- 15. Площадь треугольника:Теорема тангенсов:
- 16. Сферическая тригонометрия, являющаяся частью сферической геометрии, рассматривает
- 17. При каждом сокращении сердца по всему организму
- 18. Сложение гармоник дает колебание более сложной формы,
- 19. Почему летом теплее, чем зимой?Все дело в
- 20. ТРИГОНОМЕТРИЯ СферыАстрономияГеодезияКартографияМеханикаОптика Акустика применения СтроительствоАрхитектураДизайнНавигацияМедицинаМузыка Спорт
- 21. Слайд 21
- 22. История вторая- «ЭЙЛЕР»
- 23. Слайд 23
- 24. Ответы:Тригонометрия – это просто и понятно !Вариант
- 25. Работа
- 26. Групповая работа1 ГРУППА.В треугольнике АВС АС
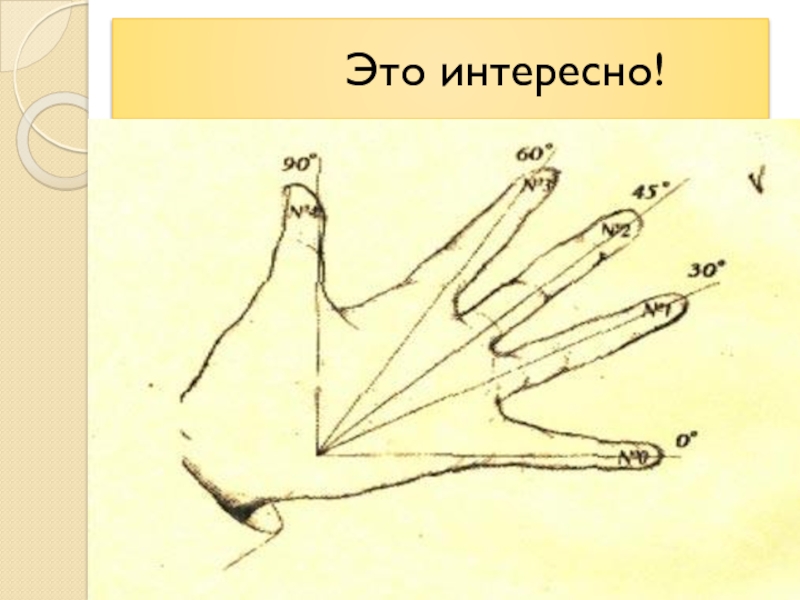
- 27. Это интересно!
- 28. История третья- «АРХИМЕД»
- 29. Подведение итогов урока:Сегодня на уроке я повторил
- 30. Домашнее задание
- 31. Слайд 31
- 32. Проверь себяНайти ширину реки.
- 33. БашняИзмерить высоту.
- 34. Слайд 34
- 35. Источники информации: http://laila50.livejournal.com/111671.htmlhttp://blogs.mail.ru/mail/kareglazka_liana/726E0A12FACCD455.htmlhttp://www.daviddarling.info/encyclopedia/A/Archimedes_and_the_burning_mirrors.htmlhttp://www.krugosvet.ru/enc/nauka_i_tehnika/matematika/ARHIMED.html?page=0,3http://kid-mathematics.narod.ru/eiler.htmhttp://flotprom.ru/publications/history/slava/eiler/Н.И. Кованцов «Математика и романтика»
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Мир тригонометрии
Общеобразовательная школа І-ІІІ ступеней №2 отдела образования
администрации города Кировское
Слайд 2«Великая книга природы может быть прочтена только теми, кто знает
язык, на котором она написана, и этот язык – математика.»
Галилео Галилей(1564 – 1642)
Слайд 5Мир тригонометрии: основные тригонометрические тождества
Цели урока:
образовательные -
систематизация уже имеющихся знаний по тригонометрии, отработка навыков преобразования тригонометрических
выраженийвоспитательные - воспитание самостоятельности, работоспособности, способности к сотрудничеству, воспитание патриотизма
развивающие - развитие коммуникативных способностей, навыков сотрудничества, повышение интеллектуального уровня, кругозора, повышение мотивации к изучению математики
Задачи урока:
- знакомство учащихся с историей математики
-повторение ранее изученного материала по тригонометрии
-повторение формул тригонометрии
- отработка навыка преобразования тригонометрических выражений с помощью основных тригонометрических формул
Слайд 6Актуализация опорных знаний:
Сформулируйте определение синуса острого угла в прямоугольном треугольнике,
косинуса и тангенса .
Найдите синус, косинус и тангенс острого
угла в прямоугольном треугольнике, противолежащий катет которого равен 8, а гипотенуза равна 10.Назовите знаки тригонометрических функций по четвертям.
Что такое 1 радиан?
Слайд 7Актуализация опорных знаний:
Перевести:
в радианы 30°,45°,60°,90,270°,-720°
в градусы π, π/3,
π/2, -3π, π/18
Может ли синус быть равным
0,75; 5/3; -0,35; 0;
√3 - 2 ?Слайд 8 Переход от градусной меры углов к радианной Переход от радианной меры
углов к градусной
Вариант №1
1. Переведите данные числа из градусной
меры в радианную меру: --45, 602. Переведите данные числа из радианной меры в градусную: п/6
Вариант №2
Переведите данные числа из градусной меры в радианную меру: -1080 , 390
2. Переведите данные числа из радианной меры в градусную: п/10
Вариант №3
1. Переведите данные числа из градусной меры в радианную меру: 40, 1200
2. Переведите данные числа из радианной меры в градусную: 5.
Слайд 10Тригономе́трия
(от греч. τρίγονο (треугольник) и греч. μετρειν (измерять), то
есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции
и их приложения к геометрии. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре.Слайд 11Первые тригонометрические таблицы были, вероятно, составлены Гиппархом Никейским (180—125 лет
до н. э.). Гиппарх был первым, кто свёл в таблицы соответствующие величины
дуг и хорд для серии углов. Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд.Слайд 13Разделы тригонометрии
Тригонометрия делится на плоскую, или прямолинейную, и сферическую тригонометрию.
Теория тригонометрических функций (гониометрия) и её приложения к решению плоских
прямоугольных и косоугольных треугольников мы с вами изучаем в средней школеСлайд 16Сферическая тригонометрия, являющаяся частью сферической геометрии, рассматривает соотношения между сторонами
и углами треугольников на сфере, образованных дугами больших кругов на
сфере.Слайд 17
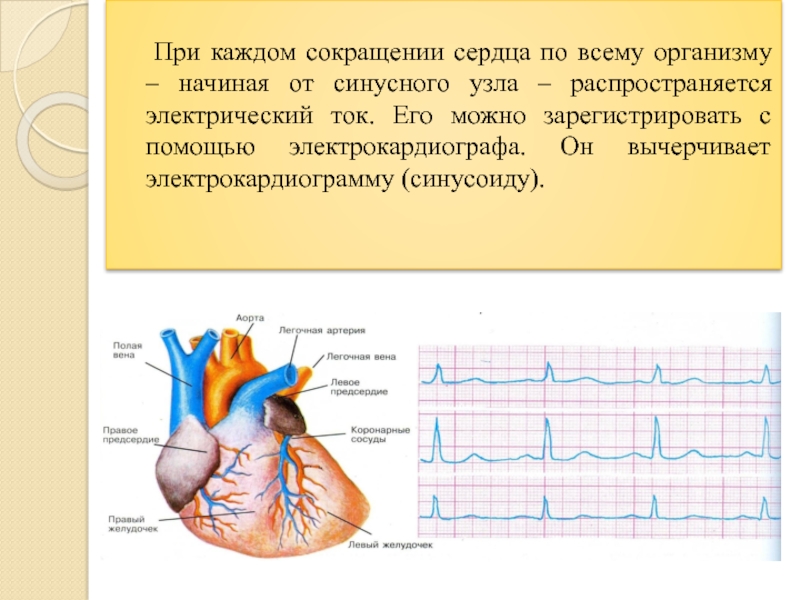
При каждом сокращении сердца по всему организму – начиная от
синусного узла – распространяется электрический ток. Его можно зарегистрировать с
помощью электрокардиографа. Он вычерчивает электрокардиограмму (синусоиду).Слайд 18
Сложение гармоник дает колебание более сложной формы, а естественные, природные
звуки и звуки музыкальных инструментов складываются из большого количества гармоник.
Слайд 19Почему летом теплее, чем зимой?
Все дело в наклоне земной оси
по отношению к плоскости земной орбиты
Зимой в умеренных широтах солнце
невысоко поднимается над горизонтом, его лучи лишь скользят по земле. Летом в моменты наивысшего подъёма над горизонтом солнце приближается к зениту, его лучи падают почти отвесно на те же участки земного шара. ПОТОК ЭНЕРГИИ, ИДУЩЕЙ ОТ Солнца, одинаков во все времена года. Но в зависимости от наклона солнечных лучей она по-разному распределяется по земной поверхности. Больше всего её приходится на заданный участок поверхности при отвесном падении света. Чем меньше угол, который образуют лучи с поверхностью, тем меньше их приходится на тот же участок.
Слайд 20ТРИГОНОМЕТРИЯ
Сферы
Астрономия
Геодезия
Картография
Механика
Оптика
Акустика
применения
Строительство
Архитектура
Дизайн
Навигация
Медицина
Музыка
Спорт
Слайд 21 Формулы приведения
y
π/2+t π/2 π/2-t
1). Определить четверть
π – t 2π+t 2).Определить знак функции
π х 3).От ОХ – не меняем на кофункцию
2π-t
π+t От ОУ – меняем на ко функцию.
3π/2+t
3π/2-t 3π/2
Слайд 23
Тест
2 вариант
Упростить выражение:
7 cos2а +7sin2а - 5
а) 1+cos2а; б) 2; в) –12; г) 12
2) Упростить выражение:
5 – 4 sin2а - 4cos2а
а) 1; б) 9; в) 1+8sin2а; г) 1+cos2а.
3) Упростить выражение:
(1 – cos2а): cos2а – tg2а
а) ctg2а; б) 0; в) ctg2а - tg2а; г) 2tg2а
4) Упростить выражение
cos4х + sin2х·cos2х
а) cos2x; б) 2sin2х; в)- cos2х; г) cos4х
1 вариант
Упростить выражение
9 cos2а+ 9sin2а - 10
а) -1 б) 0 в) sin2а г) 10
2) Упростить выражени
8 – 3 sin2а - 3cos2а
а)1+ sin2а б) cos2а-1 в) 1 г) 5
3) Упростить выражение:
(1 –sin2а): sin2а– сtg2а
а) sin2а ; б) 0; в) 2сtg2а г) sin2а
4) Упростить выражение
sin4х + sin2х·cos2х
а) sin4х б) 2sin2х в) sin 2x г) cos2x
Слайд 24Ответы:
Тригонометрия –
это просто и понятно !
Вариант 1: 1а,
2г, 3б, 4в Вариант 2: 1б, 2а, 3б, 4а
Слайд 25 Работа с формулами. Подготовка
к экзаменам
Дано cost=0,4; 90°
Решение:
1 способ. 2 способ. cos = 2/5 ; СВ=
1)sin²t + cos²t=1, А
sin²t=1 - cos²t, 5 Т.К. t Є 2 ч, то sin t > 0 .
Значит, sin t=
sin²t=1 - 0,16, 2 2
sin²t=0,84,
Т.К. tЄ2ч, то sin t > 0 .С В
Ответ:
sint= +
sint =
Ответ: .
Слайд 26 Групповая работа
1 ГРУППА.
В треугольнике АВС АС = ВС =
5, . Найдите АВ.
Найти площадь фигуры, изображенной на рисунке
2 ГРУППА.
1)В треугольнике АВС угол С равен 90, угол А равен 60, АВ = 8. Найдите АС.
Найти площадь фигуры, изображенной на рисунке
3 ГРУППА.
В треугольнике АВС угол С равен 90,
Найдите
Найти площадь фигуры, изображенной на рисунке