Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи на доказательство № 25 из ОГЭ
Содержание
- 1. Задачи на доказательство № 25 из ОГЭ
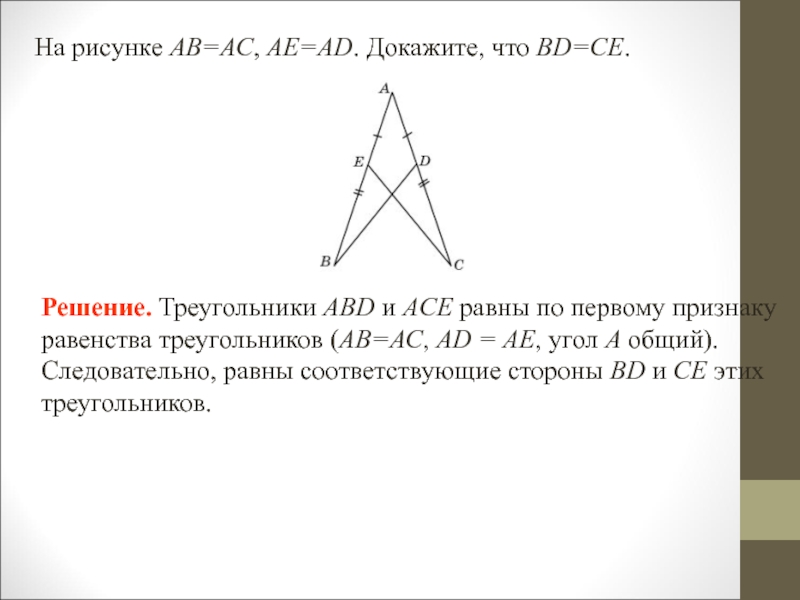
- 2. На рисунке АВ=АС, АЕ=АD. Докажите, что BD=CE. Решение.
- 3. На сторонах угла CAD отмечены точки B
- 4. На рисунке угол A равен углу B,
- 5. Точки A, B, C принадлежат одной прямой.
- 6. Точки A, B, C, D принадлежат одной
- 7. На каждой стороне правильного треугольника ABC последовательно
- 8. На продолжении каждой стороны правильного треугольника ABC
- 9. На рисунке дана фигура, у которой AD
- 10. Лучи AD и ВС пересекаются в точке
- 11. В четырехугольнике ABCD угол DAB равен углу
- 12. Треугольники АВС и А1В1С1 равны. Отрезки CD
- 13. В четырехугольнике ABCD АВ = CD и
- 14. В четырехугольнике ABCD AD = BC и
- 15. На рисунке AD = CF, AB =
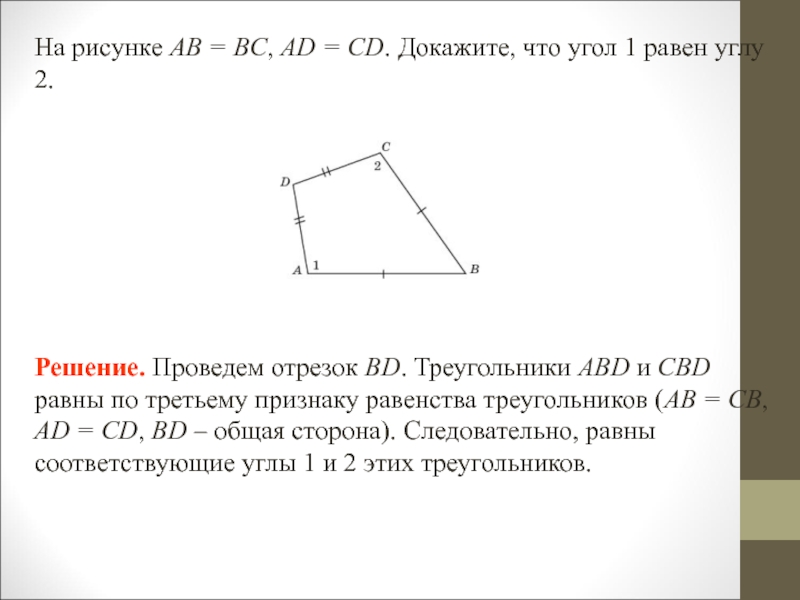
- 16. На рисунке AB = BC, AD =
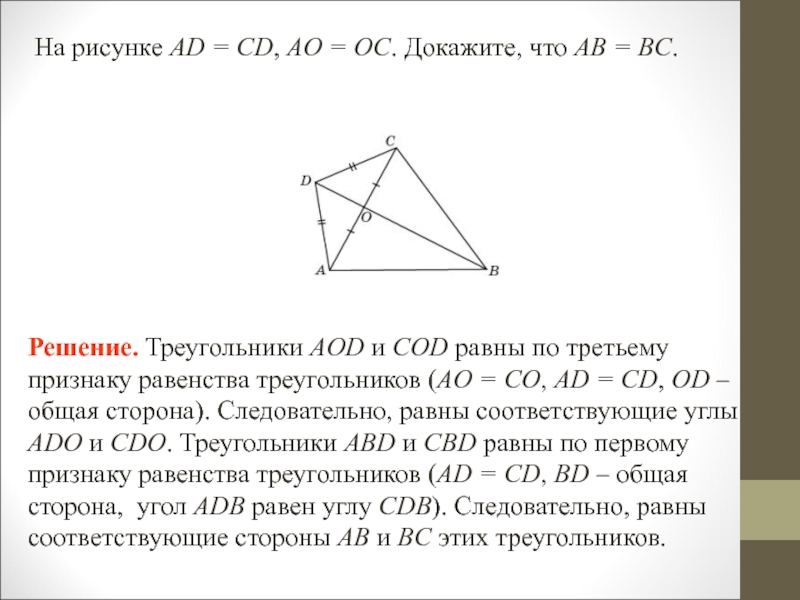
- 17. На рисунке AD = CD, AO =
- 18. На рисунке AB = BC, AD =
- 19. Треугольники АВС и BAD равны, причем точки
- 20. На рисунке АВ = CD, AD =
- 21. Докажите, что если две стороны и медиана,
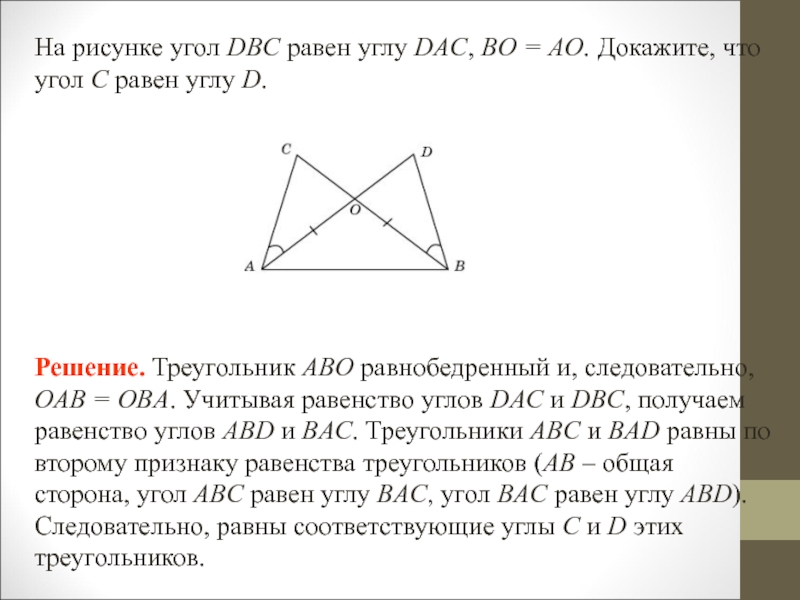
- 22. На рисунке угол DBC равен углу DAC,
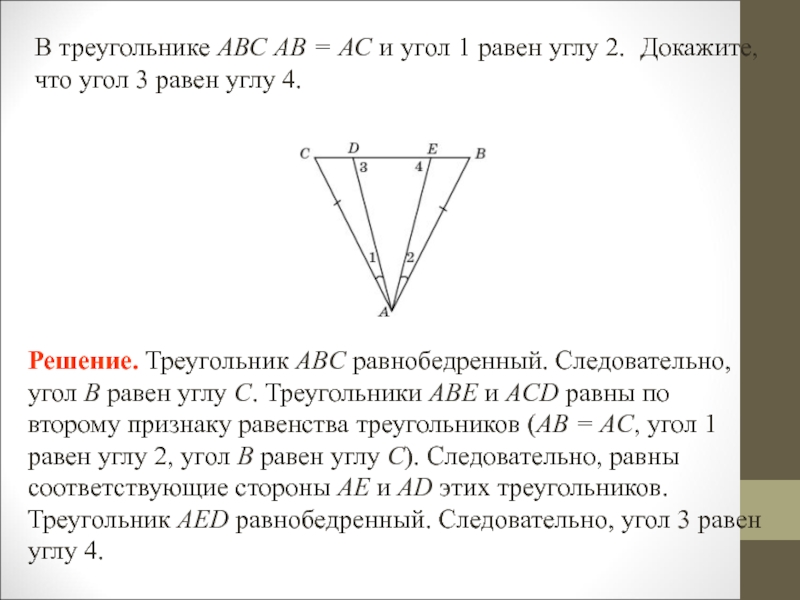
- 23. В треугольнике АВС АВ = АС и
- 24. На рисунке AD = AE, угол CAD
- 25. На рисунке CD = BD, угол 1
- 26. На рисунке угол 1 равен углу 2,
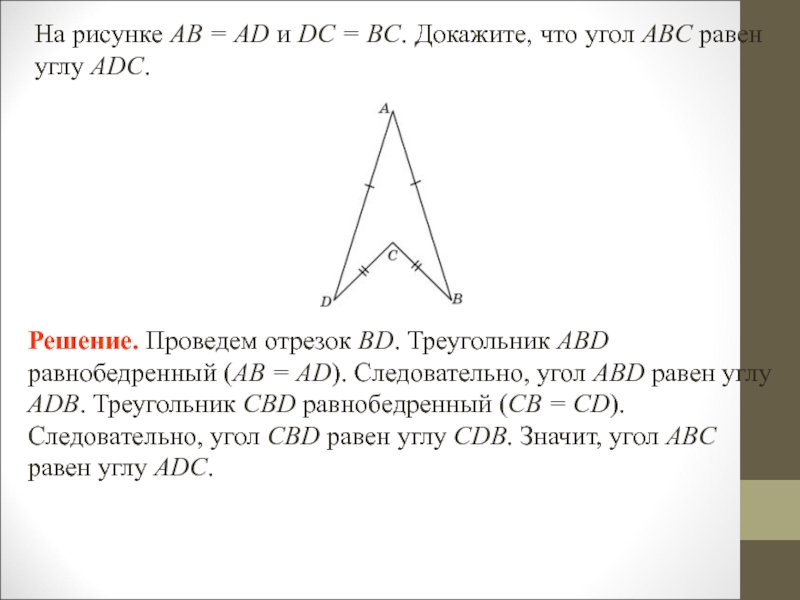
- 27. На рисунке АВ = AD и DC
- 28. На рисунке DC = BC и угол
- 29. На рисунке AB = BC, CD =
- 30. На рисунке AB = BC, угол 1
- 31. Докажите, что если противоположные углы четырехугольника равны,
- 32. Докажите, что если диагонали параллелограмма равны, то
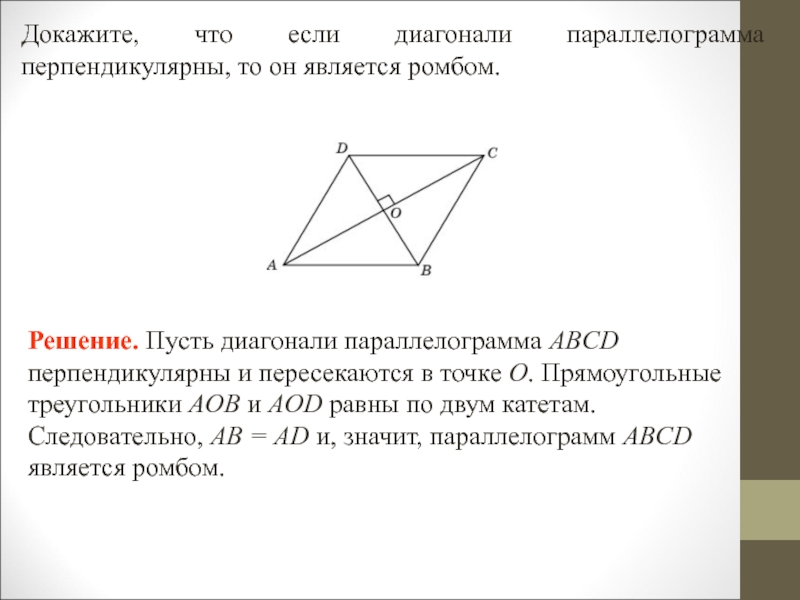
- 33. Докажите, что если диагонали параллелограмма перпендикулярны, то
- 34. Докажите, что если диагонали прямоугольника перпендикулярны, то
- 35. Докажите, что если диагонали четырехугольника пересекаются и
- 36. Докажите, что если два угла при основании трапеции равны, то трапеция – равнобедренная.
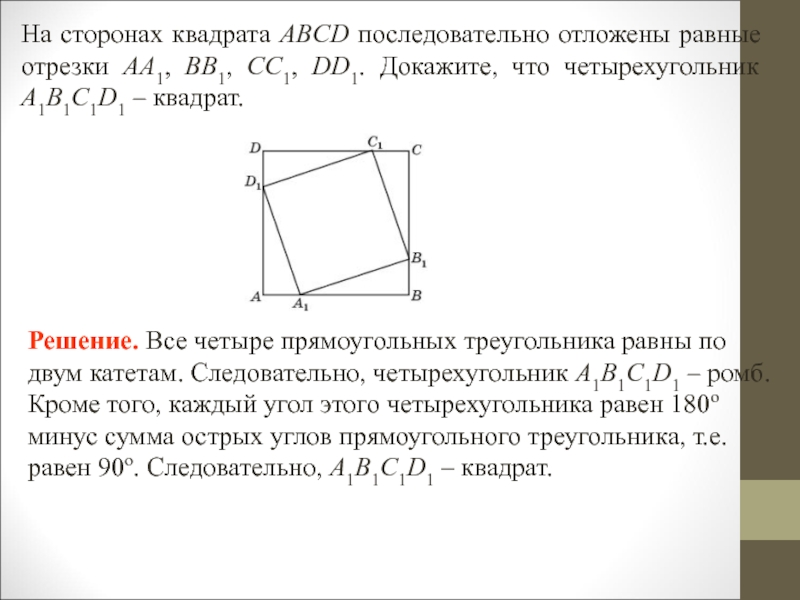
- 37. На сторонах квадрата ABCD последовательно отложены равные
- 38. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.
- 39. Докажите, что диаметр, проведенный через середину хорды
- 40. Докажите, что равные хорды окружности равноудалены от центра окружности.
- 41. Две окружности касаются внутренним образом, причем меньшая
- 42. Из концов диаметра AB окружности опущены перпендикуляры
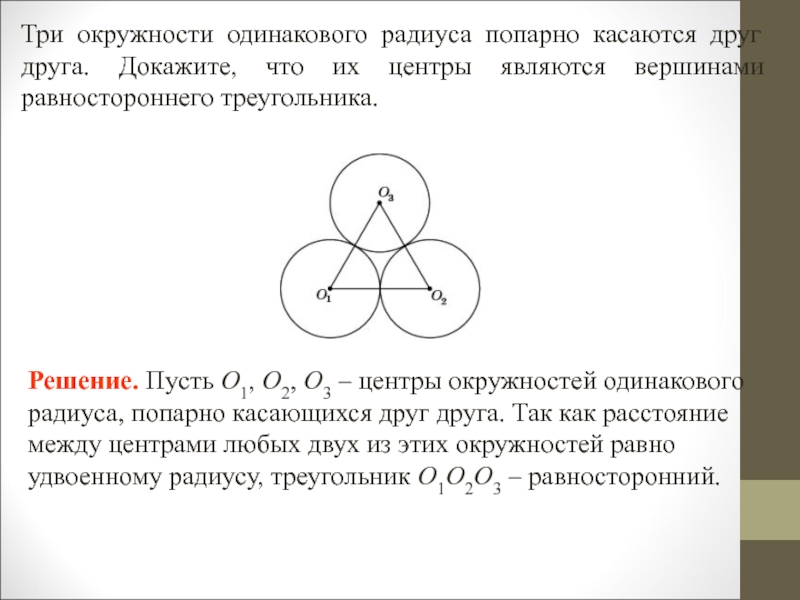
- 43. Три окружности одинакового радиуса попарно касаются друг
- 44. Скачать презентанцию
На рисунке АВ=АС, АЕ=АD. Докажите, что BD=CE. Решение. Треугольники ABD и ACE равны по первому признаку равенства треугольников (АВ=АС, АD = AE, угол A общий). Следовательно, равны соответствующие стороны BD и CE
Слайды и текст этой презентации
Слайд 3На сторонах угла CAD отмечены точки B и E так,
что точка B лежит на стороне AC, а точка E
– на стороне AD, причем AC = AD и AB = AE. Докажите, что угол CBD равен углу DEC.Решение. Треугольники ABD и ACE равны по первому признаку равенства треугольников (AC = AD, АВ=АС, угол A общий). Следовательно, равны соответствующие углы ABD и AEC. Из равенства этих углов следует равенство смежных углов CBD и DEC.
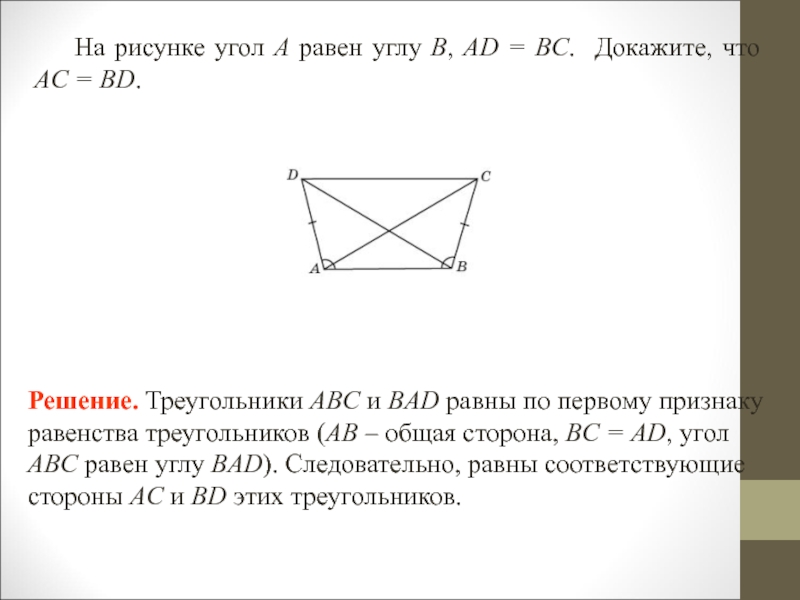
Слайд 4 На рисунке угол A равен углу B, AD = BC.
Докажите, что AC = BD.
Решение. Треугольники ABC и BAD равны
по первому признаку равенства треугольников (AB – общая сторона, BC = AD, угол ABC равен углу BAD). Следовательно, равны соответствующие стороны AC и BD этих треугольников. 
Слайд 5Точки A, B, C принадлежат одной прямой. Точки D1 и
D2 лежат по разные стороны от этой прямой. Докажите, что
если треугольники ABD1 и ABD2 равны, то треугольники BCD1 и BCD2 тоже равны.Решение. Из равенства треугольников ABD1 и ABD2 следует равенство соответствующих сторон BD1 и BD2, а также равенство соответствующих углов ABD1 и ABD2. Из равенства указанных углов следует равенство смежных с ними углов CBD1 и CBD2. Треугольники BCD1 и BCD2 равны по первому признаку равенства треугольников (BD1 = BD2, BC – общая сторона, угол CBD1 равен углу CBD2.
Слайд 6Точки A, B, C, D принадлежат одной прямой. Точки E1
и E2 лежат по разные стороны от этой прямой. Докажите,
что если треугольники ABE1 и ABE2 равны, то треугольники CDE1 и CDE2 тоже равны.Решение. Из предыдущей задачи следует, что из равенства треугольников ABE1 и ABE2 вытекает равенство треугольников BCE1 и BCE2, которое, в свою очередь, влечет равенство треугольников CDE1 и CDE2.
Слайд 7На каждой стороне правильного треугольника ABC последовательно отложены равные отрезки
AD, BE, CF. Докажите, что треугольник DEF тоже правильный.
Решение.
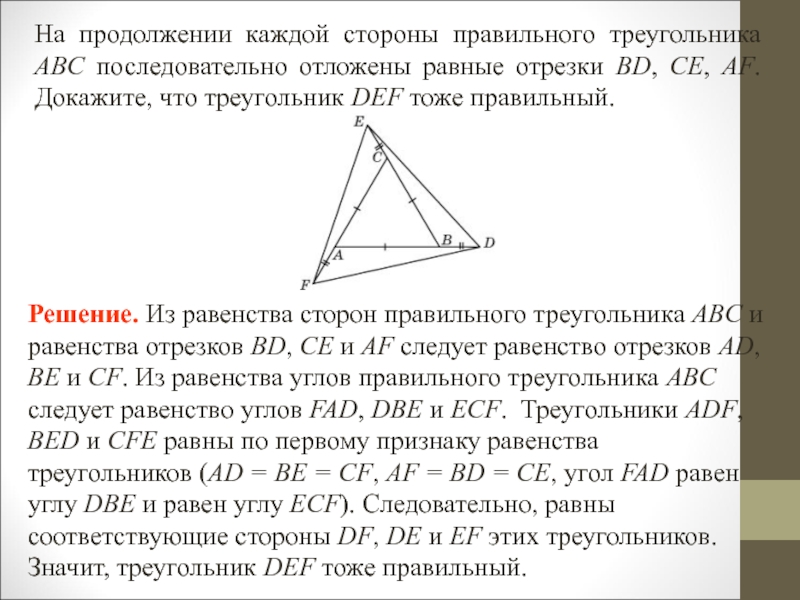
Из равенства сторон правильного треугольника и равенства отрезков AD, BE и CF следует равенство отрезков AF, CE и BD. Треугольники ADF, BED и CFE равны по первому признаку равенства треугольников (AD = BE = CF, AF = BD = CE, угол A равен углу B и равен углу C). Следовательно, равны соответствующие стороны DF, DE и EF этих треугольников. Значит, треугольник DEF тоже правильный. 
Слайд 8На продолжении каждой стороны правильного треугольника ABC последовательно отложены равные
отрезки BD, CE, AF. Докажите, что треугольник DEF тоже правильный.
Решение. Из равенства сторон правильного треугольника ABC и равенства отрезков BD, CE и AF следует равенство отрезков AD, BE и CF. Из равенства углов правильного треугольника ABC следует равенство углов FAD, DBE и ECF. Треугольники ADF, BED и CFE равны по первому признаку равенства треугольников (AD = BE = CF, AF = BD = CE, угол FAD равен углу DBE и равен углу ECF). Следовательно, равны соответствующие стороны DF, DE и EF этих треугольников. Значит, треугольник DEF тоже правильный.
Слайд 9На рисунке дана фигура, у которой AD = CF, угол
ВAC равен углу EDF, угол 1 равен углу 2. Докажите,
что треугольники АВС и DEF равны.Решение. Из равенства углов 1 и 2 следует равенство смежных углов ACB и DFE. Из равенства отрезков AD и CF следует равенство отрезков AC и DF. Треугольники ACB и DFE равны по второму признаку равенства треугольников (AC = DF, угол ВAC равен углу EDF, угол ACB равен углу DFE).
Слайд 10Лучи AD и ВС пересекаются в точке О, угол 1
равен углу 2, OC = OD. Докажите, что OA =
OB.Решение. Из равенства углов 1 и 2 следует равенство смежных с ними углов ACO и BDO. Треугольники ACO и BDO равны по второму признаку равенства треугольников (CO = DO, угол ACO равен углу BDO, угол AOC равен углу BOD). Следовательно, равны соответствующие стороны OA и OB этих треугольников.
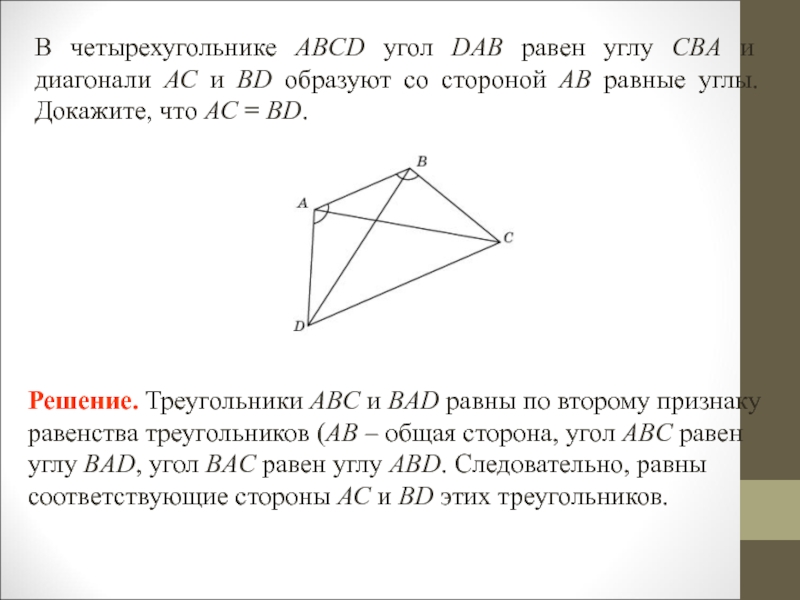
Слайд 11В четырехугольнике ABCD угол DAB равен углу CBА и диагонали
АС и BD образуют со стороной АВ равные углы. Докажите,
что АС = BD.Решение. Треугольники ABC и BAD равны по второму признаку равенства треугольников (AB – общая сторона, угол ABC равен углу BАD, угол BAC равен углу ABD. Следовательно, равны соответствующие стороны АС и BD этих треугольников.
Слайд 12Треугольники АВС и А1В1С1 равны. Отрезки CD и C1D1 образуют
со сторонами соответственно СВ и С1В1 равные углы. Докажите, что
AD = A1D1.Решение. Из равенства треугольников АВС и А1В1С1 следует равенство соответствующих сторон BC и B1C1, а также соответствующих углов B и B1. Треугольники BCD и B1C1D1 равны по первому признаку равенства треугольников (BC = B1C1, угол B равен углу B1, угол BCD равен углу B1C1D1). Следовательно, равны соответствующие стороны BD и B1D1 этих треугольников. Из равенства треугольников АВС и А1В1С1 следует равенство соответствующих сторон AB и A1B1. Следовательно, имеет место равенство отрезков AD и A1D1.
Слайд 13В четырехугольнике ABCD АВ = CD и AD = BC.
Докажите, что угол A равен углу C.
Решение. В четырехугольнике
ABCD проведем диагональ BD. Треугольники ABD и CDB равны по третьему признаку равенства треугольников (AB = CD, AD = BC, BD – общая сторона). Следовательно, равны соответствующие углы A и C этих треугольников.
Слайд 14В четырехугольнике ABCD AD = BC и AC = BD.
Докажите, что угол BAD равен углу ABC.
Решение. Треугольники ABC
и BAD равны по третьему признаку равенства треугольников (AD = BC, AC = BD, AB – общая сторона). Следовательно, равны соответствующие углы BAD и ABC. 
Слайд 15На рисунке AD = CF, AB = FE, BC =
ED. Докажите, что угол 1 равен углу 2.
Решение. Из равенства
отрезков AD и CF следует равенство отрезков AC и DF. Треугольники ABC и FED равны по третьему признаку равенства треугольников (AB = FE, BC = ED, AC = FD). Следовательно, равны соответствующие углы ACB и FDE этих треугольников, а, значит, равны и смежные с ними углы 1 и 2. 
Слайд 16На рисунке AB = BC, AD = CD. Докажите, что
угол 1 равен углу 2.
Решение. Проведем отрезок BD. Треугольники
ABD и CBD равны по третьему признаку равенства треугольников (AB = CB, AD = CD, BD – общая сторона). Следовательно, равны соответствующие углы 1 и 2 этих треугольников. 
Слайд 17На рисунке AD = CD, AO = OC. Докажите, что
AB = BC.
Решение. Треугольники AOD и COD равны по
третьему признаку равенства треугольников (AO = CO, AD = CD, OD – общая сторона). Следовательно, равны соответствующие углы ADO и CDO. Треугольники ABD и CBD равны по первому признаку равенства треугольников (AD = CD, BD – общая сторона, угол ADB равен углу CDB). Следовательно, равны соответствующие стороны AB и BC этих треугольников. 
Слайд 18На рисунке AB = BC, AD = CD. Докажите, что
AO = OC.
Решение. Треугольники ABD и CBD равны по
третьему признаку равенства треугольников (AB = CB, AD = CD, BD – общая сторона). Следовательно, равны соответствующие углы ABO и CBO. Треугольники ABO и CBO равны по первому признаку равенства треугольников (AB = CB, BO – общая сторона, угол ABO равен углу CBO). Следовательно, равны соответствующие стороны AO и CO этих треугольников. 
Слайд 19Треугольники АВС и BAD равны, причем точки С и D
лежат по разные стороны от прямой АВ. Докажите, что треугольники
CBD и DAC равны.Решение. Из равенства треугольников АВС и BAD следует равенство соответствующих сторон AC и BD, BC и AD. Треугольники CBD и DAC равны по третьему признаку равенства треугольников (CB = DA, BD = AC, CD – общая сторона.
Слайд 20На рисунке АВ = CD, AD = BC, ВЕ -
биссектриса угла АВС, а DF - биссектриса угла ADC. Докажите,
что треугольники ABE и CDF равны.Решение. Треугольники ABC и ADC равны по третьему признаку равенства треугольников (АВ = CD, AD = BC, AC – общая сторона). Следовательно, равны соответствующие углы ABC и CDA, BAC и DCA. Из равенства углов ABC и CDA следует равенство углов ABE и CDF. Треугольники ABE и CDF равны по второму признаку равенства треугольников (AB = CD, угол BAE равен углу DCF, угол ABE равен углу CDF).
Слайд 21Докажите, что если две стороны и медиана, проведенная к одной
из них, одного треугольника соответственно равны двум сторонам и медиане
другого треугольника, то такие треугольники равны.Решение. Пусть в треугольниках ABC и A1B1C1 AB = A1B1, AC = A1C1 и медиана CM равна медиане C1M1. Треугольники ACM и A1C1M1 равны по третьему признаку равенства треугольников (AM = A1M1, AC = A1C1, CM = C1M1). Следовательно, угол A равен углу A1. Треугольники ABC и A1B1C1 равны по первому признаку равенства треугольников (AB = A1B1, AC = A1C1, угол A равен углу A1).
Слайд 22На рисунке угол DBC равен углу DAC, BO = AO.
Докажите, что угол C равен углу D.
Решение. Треугольник ABO
равнобедренный и, следовательно, OAB = OBA. Учитывая равенство углов DAC и DBC, получаем равенство углов ABD и BAC. Треугольники ABC и BAD равны по второму признаку равенства треугольников (AB – общая сторона, угол ABC равен углу BAC, угол BAC равен углу ABD). Следовательно, равны соответствующие углы C и D этих треугольников. 
Слайд 23В треугольнике АВС АВ = АС и угол 1 равен
углу 2. Докажите, что угол 3 равен углу 4.
Решение. Треугольник
ABC равнобедренный. Следовательно, угол B равен углу C. Треугольники ABE и ACD равны по второму признаку равенства треугольников (AB = AC, угол 1 равен углу 2, угол B равен углу C). Следовательно, равны соответствующие стороны AE и AD этих треугольников. Треугольник AED равнобедренный. Следовательно, угол 3 равен углу 4. 
Слайд 24На рисунке AD = AE, угол CAD равен углу BAE.
Докажите, что BD = CE.
Решение. Треугольник ADE равнобедренный. Следовательно, угол
D равен углу E. Треугольники ACD и ABE равны по второму признаку равенства треугольников (AD = AE, угол D равен углу E, угол CAD равен углу BAE). Следовательно, равны соответствующие стороны CD и BE. Значит, равны и отрезки BD и CE. 
Слайд 25На рисунке CD = BD, угол 1 равен углу 2.
Докажите, что угол ACB равен углу ABC.
Решение. Треугольники ABD и
ACD равны по первому признаку равенства треугольников (AD – общая сторона, BD = CD, угол ADB равен углу ADC). Следовательно, равны соответствующие стороны AB и AC этих треугольников. Треугольник ABC равнобедренный и, значит, ACB = ABC.
Слайд 26На рисунке угол 1 равен углу 2, угол 5 равен
углу 6. Докажите, что угол 3 равен углу 4.
Решение. Треугольники
ABС и ABD равны по второму признаку равенства треугольников (AB – общая сторона, угол ABC равен углу ABD, угол BAC равен углу BAD). Следовательно, равны соответствующие стороны BC и BD этих треугольников. Треугольник BCD равнобедренный и, значит, угол 3 равен углу 4.
Слайд 27На рисунке АВ = AD и DC = BC. Докажите,
что угол ABC равен углу ADC.
Решение. Проведем отрезок BD. Треугольник
ABD равнобедренный (AB = AD). Следовательно, угол ABD равен углу ADB. Треугольник CBD равнобедренный (CB = CD). Следовательно, угол CBD равен углу CDB. Значит, угол ABC равен углу ADC.
Слайд 28На рисунке DC = BC и угол B равен углу
D. Докажите, что АВ = AD
Решение. Проведем отрезок BD.
Треугольник BCD равнобедренный (BC = DC). Следовательно, имеет место равенство DBC = BDC. Из этого равенства и равенства углов ABC и ADC следует равенство углов ABD и ADB. Значит, треугольник ABD – равнобедренный и, следовательно, АВ = AD. 
Слайд 29На рисунке AB = BC, CD = DE. Докажите, что
угол BAC равен углу CED.
Решение. Треугольник ABC – равнобедренный
и, следовательно, угол BAC равен углу BCA. Треугольник CDE – равнобедренный и, следовательно, угол DCE равен углу DEC. Углы BCA и DCE равны как вертикальные. Следовательно, угол BAC равен углу DEC. 
Слайд 30На рисунке AB = BC, угол 1 равен углу 2.
Докажите, что AD = CD.
Решение. Проведем отрезок AC. Треугольник
ABC равнобедренный (AB = BC). Следовательно, угол BAC равен углу BCA. Из этого равенства и равенства углов 1 и 2 следует равенство углов DAC и DCA. Значит, треугольник DAC равнобедренный и, следовательно, AD = CD. 
Слайд 31 Докажите, что если противоположные углы четырехугольника равны, то он –
параллелограмм.
Решение. Пусть ABCD – четырехугольник, у которого противоположные углы равны.
Так как сумма углов четырехугольника равна 360о, то сумма двух односторонних углов будет равна 180о и, следовательно, противоположные стороны этого четырехугольника параллельны, т.е. он – параллелограмм. 
Слайд 32Докажите, что если диагонали параллелограмма равны, то он является прямоугольником.
Решение. Пусть в прямоугольнике ABCD проведены диагонали AC и BD.
Треугольники ABC и BAD равны по трем сторонам. Следовательно, угол ABC равен углу BAD. В сумме эти углы составляют 180о, как односторонние углы при параллельных BC и AD и секущей AB. Следовательно, эти углы равны 90о и, значит, ABCD – прямоугольник. 
Слайд 33Докажите, что если диагонали параллелограмма перпендикулярны, то он является ромбом.
Решение. Пусть диагонали параллелограмма ABCD перпендикулярны и пересекаются в точке
O. Прямоугольные треугольники AOB и AOD равны по двум катетам. Следовательно, AB = AD и, значит, параллелограмм ABCD является ромбом. 
Слайд 34Докажите, что если диагонали прямоугольника перпендикулярны, то он является квадратом.
Решение. Пусть диагонали прямоугольника ABCD перпендикулярны и пересекаются в точке
O. Прямоугольные треугольники AOB и AOD равны по двум катетам. Следовательно, AB = AD и, значит, ABCD – квадрат. 
Слайд 35Докажите, что если диагонали четырехугольника пересекаются и точкой пересечения делятся
пополам, то этот четырехугольник – параллелограмм.
Решение. Пусть диагонали четырехугольника
ABCD пересекаются в точке O. Треугольники AOB и COD равны по двум сторонам и углу между ними. Следовательно, угол OAB равен углу OCD и, значит, отрезки AB и CD равны и параллельны. Следовательно, четырехугольник ABCD – параллелограмм. 
Слайд 37На сторонах квадрата ABCD последовательно отложены равные отрезки AA1, BB1,
CC1, DD1. Докажите, что четырехугольник A1B1C1D1 – квадрат.
Решение. Все
четыре прямоугольных треугольника равны по двум катетам. Следовательно, четырехугольник A1B1C1D1 – ромб. Кроме того, каждый угол этого четырехугольника равен 180о минус сумма острых углов прямоугольного треугольника, т.е. равен 90о. Следовательно, A1B1C1D1 – квадрат. 
Слайд 39Докажите, что диаметр, проведенный через середину хорды той же окружности,
отличной от диаметра, перпендикулярен этой хорде.
Решение. Пусть AB –
диаметр окружности с центром O, проходящий через середину E хорды CD, отличной от диаметра. В равнобедренном треугольнике OCD отрезок OE является медианой и, следовательно, высотой. Значит, AB перпендикулярна CD. 
Слайд 41Две окружности касаются внутренним образом, причем меньшая окружность проходит через
центр большей. Докажите, что всякая хорда большей окружности, проходящая через
точку касания, делится меньшей окружностью пополам.
Слайд 42Из концов диаметра AB окружности опущены перпендикуляры AA1 и BB1
на касательную. Докажите, что точка касания C является серединой отрезка
A1B1.
Слайд 43Три окружности одинакового радиуса попарно касаются друг друга. Докажите, что
их центры являются вершинами равностороннего треугольника.
Решение. Пусть O1, O2,
O3 – центры окружностей одинакового радиуса, попарно касающихся друг друга. Так как расстояние между центрами любых двух из этих окружностей равно удвоенному радиусу, треугольник O1O2O3 – равносторонний. 
