ЗАДАЧИ НА ПОСТРОЕНИЕ

Содержание

1. ЗАДАЧИ НА ПОСТРОЕНИЕ
2. Дано:№ 313Построить:∆ ABC, где BD - медианаАнализ:ABCDABBCBDB1
3. Описание построения:1. Строим ∆BCB1 по трём
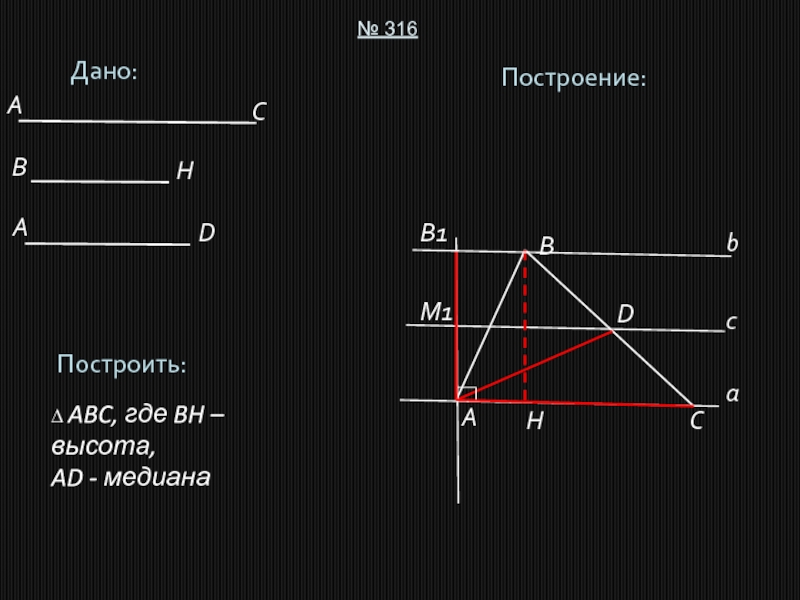
4. Дано:№ 316Построить:∆ ABC, где BH – высота,AD
5. Описание построения:1. Строим две перпендикулярные прямые
6. Дано:№ 316Построить:∆ ABC, где BH – высота,AD - медианаПостроение:ABCDACBDHHAaM1сB1b
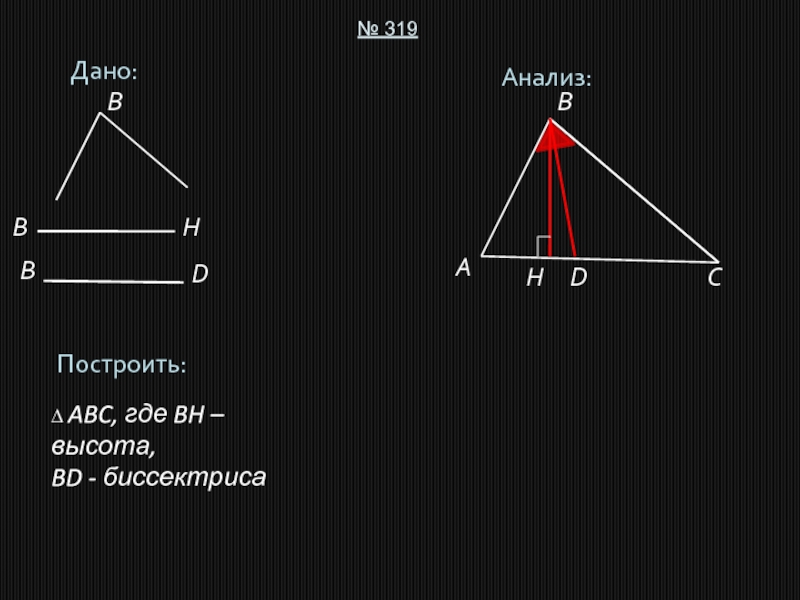
7. Дано:№ 319Построить:∆ ABC, где BH – высота,BD - биссектрисаАнализ:ABCDBBDHHB
8. Описание построения:1. Построим прямоугольный треугольник HBD
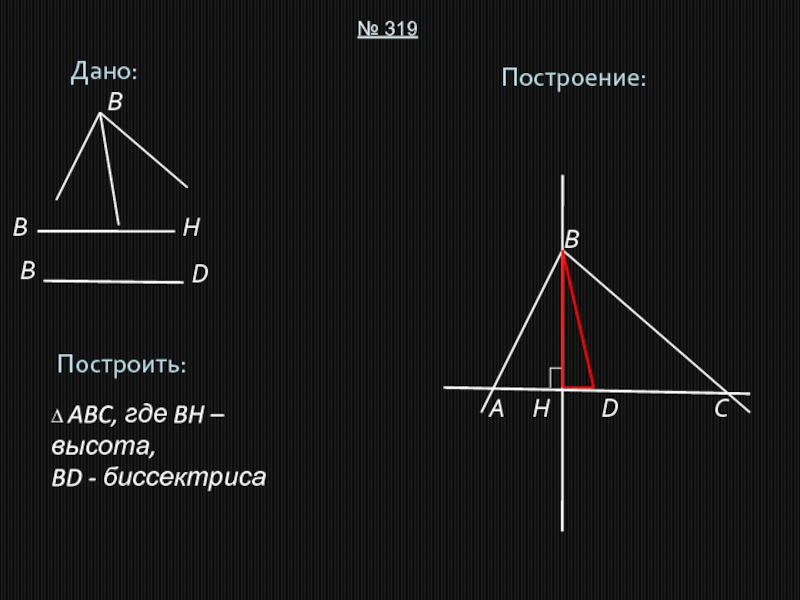
9. Дано:№ 319Построить:∆ ABC, где BH – высота,BD - биссектрисаПостроение:ABCDBBDHHB
10. Слайд 10
11. Скачать презентанцию

Дано:№ 313Построить:∆ ABC, где BD - медианаАнализ:ABCDABBCBDB1

Слайды и текст этой презентации

Слайд 1Задачи на построение
Геометрия 7 класс по Л.С. Атанасяну
Махмудова Наталья Юрьевна
учитель

математики МБОУ СОШ № 18
имени Э.Д.Потапова г.Мичуринска

Задачи на построениеГеометрия 7 класс по Л.С. АтанасянуМахмудова Наталья Юрьевнаучитель математики МБОУ СОШ № 18имени Э.Д.Потапова г.Мичуринска

Слайд 2Дано:
№ 313
Построить:
∆ ABC, где BD - медиана
Анализ:
A
B
C
D
A
B
B
C
B
D
B1

Слайд 3Описание построения:
1. Строим ∆BCB1 по трём сторонам (BB1 =

2BD, CB1 = AB).
2. Строим точку D –

середину BB1.
3.* На продолжении луча CD от точки D откладываем отрезок, равный CD (получили точку A).
4. Проводим сторону AB.
5. ∆ABC – искомый.

Задача имеет решение и при том только одно, если для отрезков AB, BC и 2BD выполняется неравенство треугольника.

Описание построения:1. Строим ∆BCB1 по трём сторонам (BB1 = 2BD, CB1 = AB).2. Строим

Слайд 4Дано:
№ 316
Построить:
∆ ABC, где BH – высота,
AD - медиана
Анализ:
A
B
C
D
A
C
B
D
H
H
A
Если прямые

a и b параллельны, то середины всех отрезков с концами,

лежащими на этих прямых, находятся на прямой с, параллельной a и b, и равноудалённой от этих прямых
(№ 282).

Дано:№ 316Построить:∆ ABC, где BH – высота,AD - медианаАнализ:ABCDACBDHHAЕсли прямые a и b параллельны, то середины всех

Слайд 5Описание построения:
1. Строим две перпендикулярные прямые (получили точку A).
На

одной из сторон прямого угла от точки A откладываем отрезок

равный HB (получили точку B1).
3. От точки A на прямой a откладываем отрезок равный AC (получили точку C).
4. Строим точку M1 – середину отрезка AB1.
5. Через точку M1 проводим прямую c, параллельную прямой a.
6. Через точку B1 проводим прямую b, параллельную прямой a
7. Из точки A раствором циркуля равным AD проводим дугу до пересечения с прямой c (получили точку D).
8. Через точки C и D проводим прямую (получили точку B).
9. Проводим сторону AB.
10. ∆ABC – искомый.

Задача не всегда имеет решение. Если решение есть, то оно единственное.

Описание построения:1. Строим две перпендикулярные прямые (получили точку A).На одной из сторон прямого угла от точки

Слайд 6Дано:
№ 316
Построить:
∆ ABC, где BH – высота,
AD - медиана
Построение:
A
B
C
D
A
C
B
D
H
H
A
a
M1
с
B1
b

Слайд 7Дано:
№ 319
Построить:
∆ ABC, где BH – высота,
BD - биссектриса
Анализ:
A
B
C
D
B
B
D
H
H
B

Слайд 8Описание построения:
1. Построим прямоугольный треугольник HBD по гипотенузе и

катету.
Проведём биссектрису данного угла B (получим угол ABD).
Достроим угол DBH

треугольника HBD до угла DBA, равного половине угла A (получим точку A).
4. Достроим угол ABD до угла ABC (получим точку C)
5. ∆ABC – искомый.

Задача всегда имеет решение и при том единственное.

Описание построения:1. Построим прямоугольный треугольник HBD по гипотенузе и катету.Проведём биссектрису данного угла B (получим угол

Слайд 9Дано:
№ 319
Построить:
∆ ABC, где BH – высота,
BD - биссектриса
Построение:
A
B
C
D
B
B
D
H
H
B

Слайд 10

Скачать презентацию

Теги

Разделы презентаций

ЗАДАЧИ НА ПОСТРОЕНИЕ

Содержание

Слайды и текст этой презентации

Слайд 1Задачи на построение
Геометрия 7 класс по Л.С. Атанасяну
Махмудова Наталья Юрьевна
учитель

математики МБОУ СОШ № 18
имени Э.Д.Потапова г.Мичуринска

Слайд 2Дано:
№ 313
Построить:
∆ ABC, где BD - медиана
Анализ:
A
B
C
D
A
B
B
C
B
D
B1

Слайд 3Описание построения:
1. Строим ∆BCB1 по трём сторонам (BB1 =

2BD, CB1 = AB).
2. Строим точку D –

Слайд 4Дано:
№ 316
Построить:
∆ ABC, где BH – высота,
AD - медиана
Анализ:
A
B
C
D
A
C
B
D
H
H
A
Если прямые

a и b параллельны, то середины всех отрезков с концами,

Слайд 5Описание построения:
1. Строим две перпендикулярные прямые (получили точку A).
На

одной из сторон прямого угла от точки A откладываем отрезок

Слайд 6Дано:
№ 316
Построить:
∆ ABC, где BH – высота,
AD - медиана
Построение:
A
B
C
D
A
C
B
D
H
H
A
a
M1
с
B1
b

Слайд 7Дано:
№ 319
Построить:
∆ ABC, где BH – высота,
BD - биссектриса
Анализ:
A
B
C
D
B
B
D
H
H
B

Слайд 8Описание построения:
1. Построим прямоугольный треугольник HBD по гипотенузе и

катету.
Проведём биссектрису данного угла B (получим угол ABD).
Достроим угол DBH

Слайд 9Дано:
№ 319
Построить:
∆ ABC, где BH – высота,
BD - биссектриса
Построение:
A
B
C
D
B
B
D
H
H
B

Слайд 10

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

ЗАДАЧИ НА ПОСТРОЕНИЕ

Содержание

Слайды и текст этой презентации

Слайд 1Задачи на построениеГеометрия 7 класс по Л.С. АтанасянуМахмудова Наталья Юрьевнаучитель

математики МБОУ СОШ № 18имени Э.Д.Потапова г.Мичуринска

Слайд 2Дано:№ 313Построить:∆ ABC, где BD - медианаАнализ:ABCDABBCBDB1

Слайд 3Описание построения:1. Строим ∆BCB1 по трём сторонам (BB1 =

2BD, CB1 = AB).2. Строим точку D –

Слайд 4Дано:№ 316Построить:∆ ABC, где BH – высота,AD - медианаАнализ:ABCDACBDHHAЕсли прямые

a и b параллельны, то середины всех отрезков с концами,

Слайд 5Описание построения:1. Строим две перпендикулярные прямые (получили точку A).На

одной из сторон прямого угла от точки A откладываем отрезок

Слайд 6Дано:№ 316Построить:∆ ABC, где BH – высота,AD - медианаПостроение:ABCDACBDHHAaM1сB1b

Слайд 7Дано:№ 319Построить:∆ ABC, где BH – высота,BD - биссектрисаАнализ:ABCDBBDHHB

Слайд 8Описание построения:1. Построим прямоугольный треугольник HBD по гипотенузе и

катету.Проведём биссектрису данного угла B (получим угол ABD).Достроим угол DBH

Слайд 9Дано:№ 319Построить:∆ ABC, где BH – высота,BD - биссектрисаПостроение:ABCDBBDHHB

Слайд 10

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Задачи на построение
Геометрия 7 класс по Л.С. Атанасяну
Махмудова Наталья Юрьевна
учитель

математики МБОУ СОШ № 18
имени Э.Д.Потапова г.Мичуринска

Слайд 2Дано:
№ 313
Построить:
∆ ABC, где BD - медиана
Анализ:
A
B
C
D
A
B
B
C
B
D
B1

Слайд 3Описание построения:
1. Строим ∆BCB1 по трём сторонам (BB1 =

2BD, CB1 = AB).
2. Строим точку D –

Слайд 4Дано:
№ 316
Построить:
∆ ABC, где BH – высота,
AD - медиана
Анализ:
A
B
C
D
A
C
B
D
H
H
A
Если прямые

Слайд 5Описание построения:
1. Строим две перпендикулярные прямые (получили точку A).
На

Слайд 6Дано:
№ 316
Построить:
∆ ABC, где BH – высота,
AD - медиана
Построение:
A
B
C
D
A
C
B
D
H
H
A
a
M1
с
B1
b

Слайд 7Дано:
№ 319
Построить:
∆ ABC, где BH – высота,
BD - биссектриса
Анализ:
A
B
C
D
B
B
D
H
H
B

Слайд 8Описание построения:
1. Построим прямоугольный треугольник HBD по гипотенузе и

катету.
Проведём биссектрису данного угла B (получим угол ABD).
Достроим угол DBH

Слайд 9Дано:
№ 319
Построить:
∆ ABC, где BH – высота,
BD - биссектриса
Построение:
A
B
C
D
B
B
D
H
H
B