Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи на построениес помощью циркуля и линейки
Содержание
- 1. Задачи на построениес помощью циркуля и линейки
- 2. Услышишь - забудешь, Увидишь - запомнишь, Построишь
- 3. Решение задач на построение осуществляется в 4
- 4. Основные задачи на построение Построение отрезка, равного
- 5. Техника безопасности при работе с циркулем Циркуль
- 6. Задача №1. Построение отрезка, равного данному.Дано: OA
- 7. Задача №2. Построение прямой, проходящей через данную
- 8. Задача №3. Построение прямой, проходящей через данную
- 9. Задача №4. Построение угла, равного данному.Дано: BAC,Построить:
- 10. Задача №5. Построение биссектрисы угла.Дано: ABCПостроить: BD
- 11. Задача №6. Построение середины отрезка.Дано: отрезок AB.Построить:
- 12. Практическое заданиеВариант №1. Разделить отрезок на
- 13. Карточки учащимся для рефлексииФамилия имя________________________________________________
- 14. 1. Индивидуальное практическое домашнее задание .Вариант №1.Построить
- 15. СПАСИБО за урок
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Геометрия-7
Задачи на построение
с помощью циркуля и линейки
Разработала учитель математики МБОУ
СОШ №12 МО Усть-Лабинский район Науменко А.А.
Слайд 2Услышишь - забудешь,
Увидишь - запомнишь,
Построишь - поймёшь. Конфуций
В геометрии выделяют задачи
на построение, которые можно решить только с помощью двух инструментов:
циркуля и линейки без масштабных делений.Линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки; с помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку.
Слайд 3Решение задач на построение осуществляется в 4 этапа:
Решением задачи на
построение называется фигура, удовлетворяющая условиям задачи.
В 7 классе мы решаем
самые простые задачи на построение, поэтому иногда достаточно только второго пункта алгоритма (или второго и третьего).Найти решение задачи на построение – значит свести ее к конечному числу основных построений после выполнения которых, искомая фигура будет уже считаться построенной.
анализ;
построение;
доказательство;
исследование.
Слайд 4Основные задачи на построение
Построение отрезка, равного данному;
Построение
прямой, проходящей через данную точку и перпендикулярную к данной прямой
(точка не лежит на данной прямой); Построение прямой, проходящей через данную точку и перпендикулярную к данной прямой (точка лежит на данной прямой);
Построение угла, равного данному;
Построение биссектрисы угла;
Построение середины отрезка.
Слайд 5Техника безопасности
при работе с циркулем
Циркуль лежит с правой
стороны, острием к себе
Без разрешения учителя циркуль не берем
Передаем товарищу тупым концом Чертим – упор на острие
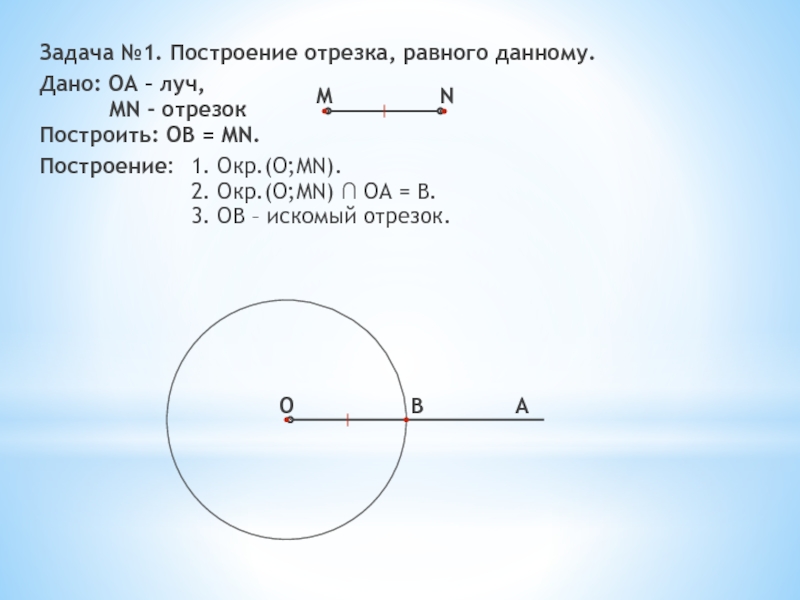
Слайд 6Задача №1. Построение отрезка, равного данному.
Дано: OA – луч,
MN -
отрезок
Построить: OB = MN.
Построение:
1. Окр.(О;МN).
M
NО А
В
2. Окр.(О;МN) ∩ ОА = В.
3. ОВ – искомый отрезок.
Слайд 7Задача №2. Построение прямой, проходящей через данную точку и перпендикулярную
к данной прямой.
Дано: прямая a,
M ∉ a.
Построить: b⊥a, M ∈
b.Построение:
1. Окр.(M;r), r – произвольный радиус.
a
М
А
А1
K
b
2. Окр.(M;r) ∩ a = A; А1.
3. Окр.(A;AM), Окр.(А1; А1 M).
4. Окр.(A;AM) ∩ Окр.(А1; А1 M) = K, M.
5. MK = b – искомая прямая, b⊥a.
Слайд 8Задача №3. Построение прямой, проходящей через данную точку, лежащую на
прямой, и перпендикулярную к данной прямой.
Дано: прямая a,
O ∈ a.
Построить:
b⊥a, O ∈ b, O ∈ a.Построение:
1. Окр.(O;r), r – произвольный радиус;
a
А
B
C
O
2. Окр.(O;r) ∩ a = A, B.
3. Окр.(A;AB), Окр.(B;AB).
4. Окр.(A;AB) ∩ Окр.(B;AB) = C.
5. OC⊥AB, OC=b, OC⊥a, b – искомая прямая.
b
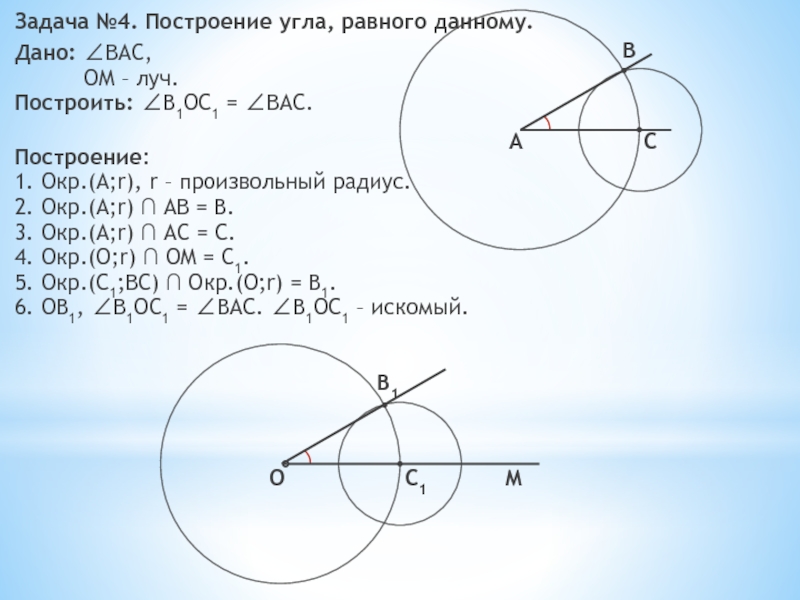
Слайд 9Задача №4. Построение угла, равного данному.
Дано: BAC,
Построить: B1OC1 = BAC.
Построение:
1.
Окр.(A;r), r – произвольный радиус.
А
СВ
О М
С1
В1
OM – луч.
2. Окр.(A;r) ∩ AB = B.
3. Окр.(A;r) ∩ AC = C.
4. Окр.(O;r) ∩ OM = C1.
5. Окр.(C1;BС) ∩ Окр.(O;r) = B1.
6. OB1, B1OC1 = BAC. B1OC1 – искомый.
Слайд 10Задача №5. Построение биссектрисы угла.
Дано: ABC
Построить: BD – биссектриса ABC.
Построение:
1.
Окр.(B;r), r – произвольный радиус.
B
СA
M
N
D
2. Окр.(B;r) ∩ AB = M.
3. Окр.(B;r) ∩ BC = N.
4. Окр.(M;r) ∩ Окр.(N;r) = D.
5. BD – искомая биссектриса ABC, ABD=CBD.
Слайд 11Задача №6. Построение середины отрезка.
Дано: отрезок AB.
Построить: точку O –
середину отрезка AB.
Построение:
1. Окр.(A;AB).
A
BP
Q
O
2. Окр.(B;BA).
3. Окр.(A;AB) ∩ Окр.(B;BA) = P, Q.
4. PQ – прямая.
5. PQ ∩ AB = O.
6. AO = BO, O – искомая точка.
Слайд 12Практическое задание
Вариант №1. Разделить отрезок на 4 равные части.
Вариант
№2. Дан ∆АВС. Построить биссектрису ВК.
Вариант №3. Дан
∆КМN. Построить медиану МР. Слайд 141. Индивидуальное практическое домашнее задание .
Вариант №1.
Построить треугольник по данной
стороне и данному углу.
Дано: PQ – отрезок,
hkПостроить: ∆ ABC, AB=PQ, ABC =hk, BAC =
Построение. Самостоятельно описать построение и построить треугольник по данным элементам.
Вариант №2.
Построить прямоугольный треугольник по двум сторонам.
Дано: а – отрезок,
b – отрезок.
Построить: ∆ ABC, С=90о, AС=а, СВ=b
Построение. Самостоятельно описать построение и построить треугольник по данным элементам.
2. Учебник И.М.Смирнова, В.А.Смирнов. Геометрия, 7-9 классы, §20, с.87-89,
изучить теорию, отвечать на вопросы №1-6, с.90-91,№7, с.91.
Практическое задание