Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
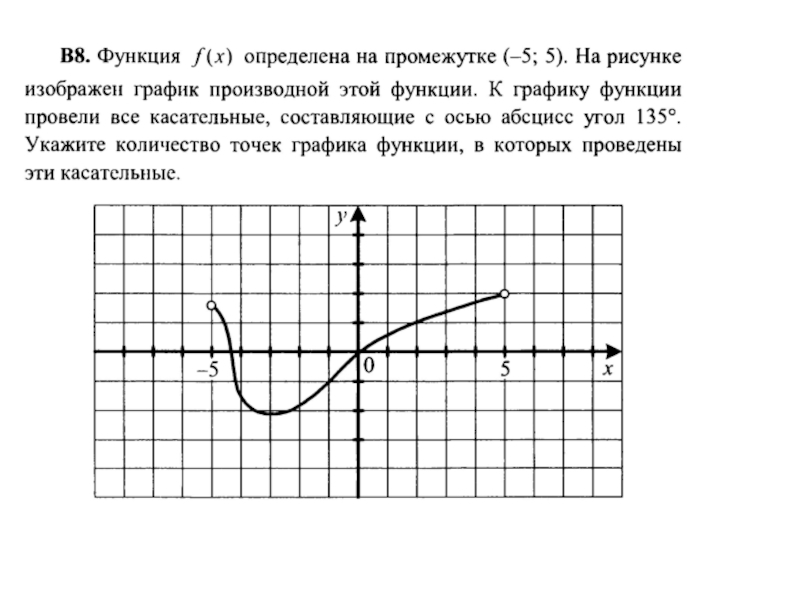
"Задачи типа В 8 на ЕГЭ по математике"
Содержание
- 1. "Задачи типа В 8 на ЕГЭ по математике"
- 2. «Бугорки и впадины»
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Вычисление точек максимума и минимума
- 8. Перечертить график производной, убрав всю лишнюю информацию.
- 9. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
- 10. Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:Ответ: −3
- 11. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
- 12. Перечертим график, оставив на координатной оси только границы [−3;
- 13. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
- 14. Строим новый график, на котором отмечаем только границы
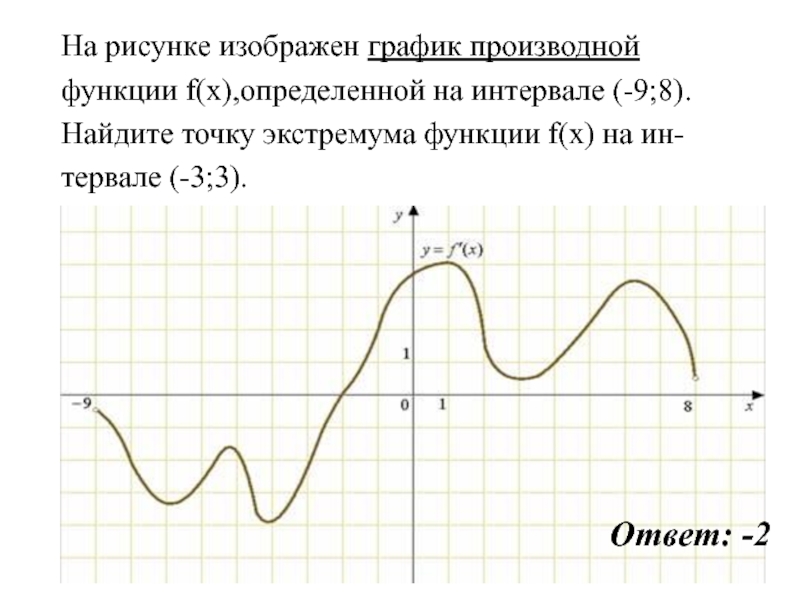
- 15. 2)На рисунке изображен график производнойфункции f(x),определенной на
- 16. На рисунке изображен график производнойфункции f(x),определенной на
- 17. Нахождение интервалов возрастания и убывания функции
- 18. Алгоритм:1. Убрать всю лишнюю информацию. На исходном графике
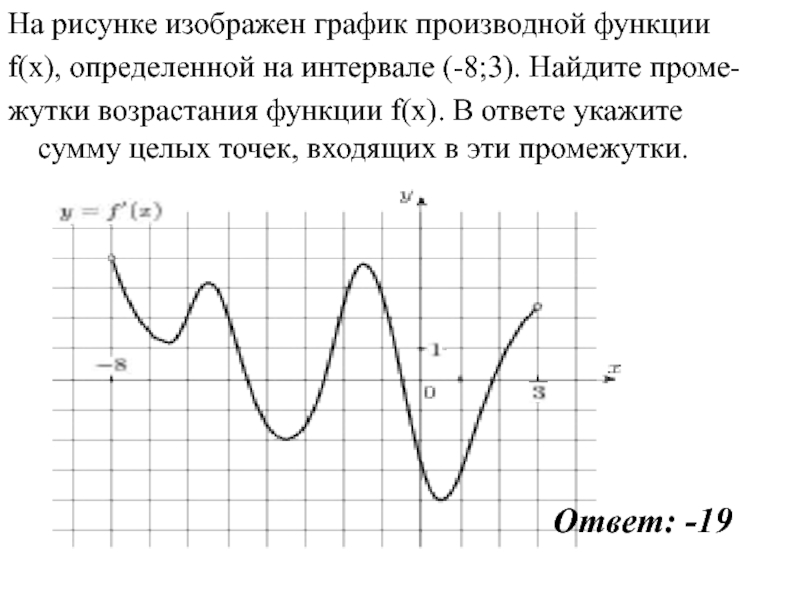
- 19. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5].
- 20. 1. Перечертим график и отметим границы [−3; 7,5], а также
- 21. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
- 22. 1. Избавимся от лишней информации. Оставим только границы [−10; 4]
- 23. На рисунке изображен график производной функцииf(x), определенной
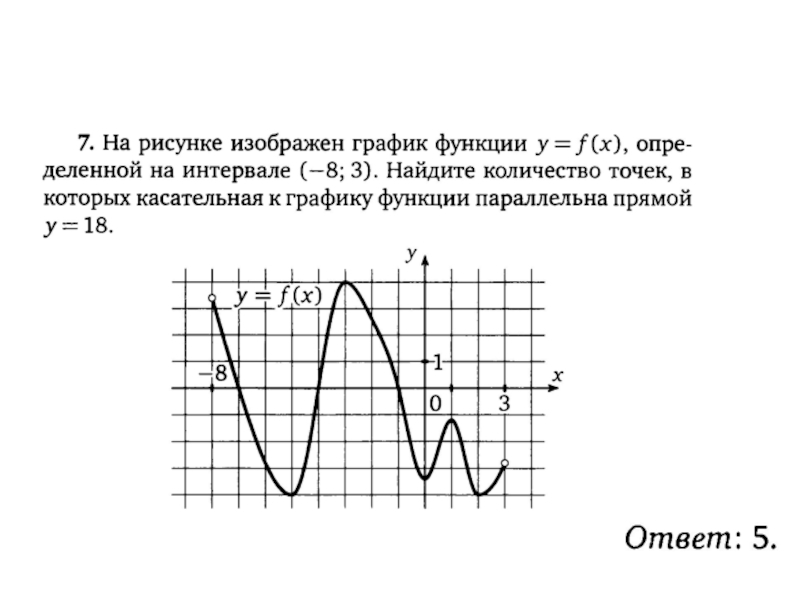
- 24. На рисунке изображен график функции , определенной
- 25. Производная функции положительна на тех интервалах, на
- 26. На рисунке изображен график функцииy=f(x),определенной на интервале
- 27. На рисунке изображён график дифференцируемой функции .
- 28. На рисунке изображен график производнойфункции f(x),определенной
- 29. На рисунке изображен график производнойфункции f(x),определенной на
- 30. На рисунке изображен график производной функции f(x),определенной
- 31. На рисунке изображен график функции y=f(x),определенной на
- 32. Нахождение наибольшего, наименьшего значения функции
- 33. На рисунке изображен график производнойфункции f(x),определенной на
- 34. На рисунке изображен график производнойфункции f(x),определенной на
- 35. На рисунке изображен график производнойфункции f(x),определенной на
- 36. На рисунке изображен график производнойфункции f(x),определенной на
- 37. На рисунке изображен график производнойфункции f(x),определенной на
- 38. На рисунке изображен график производнойфункции f(x),определенной на
- 39. На рисунке изображен график производнойфункции f(x),определенной на
- 40. На рисунке изображен график производнойфункции f(x),определенной на
- 41. Слайд 41
- 42. Слайд 42
- 43. Задачи с уравнением касательной
- 44. Алгоритм:
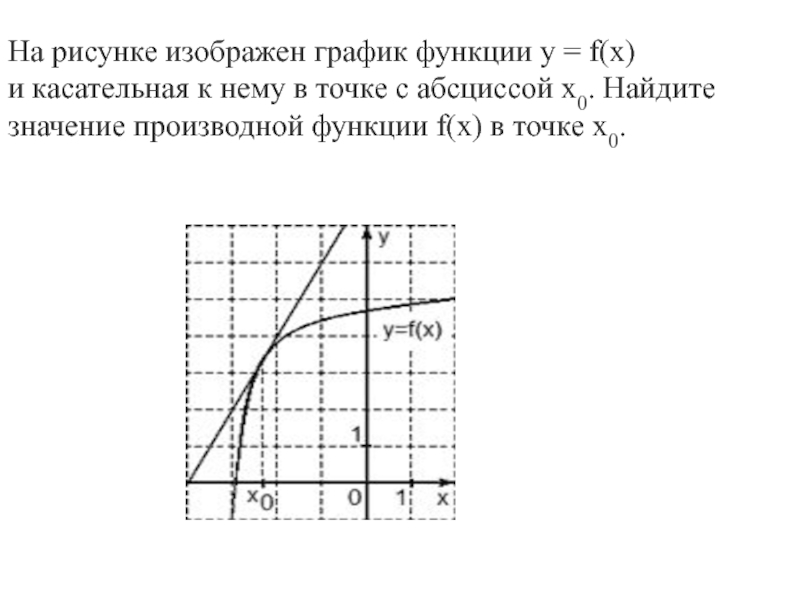
- 45. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- 46. Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения: Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.Найдем значение производной: D = Δy/Δx = 4/2 = 2.Ответ: 2
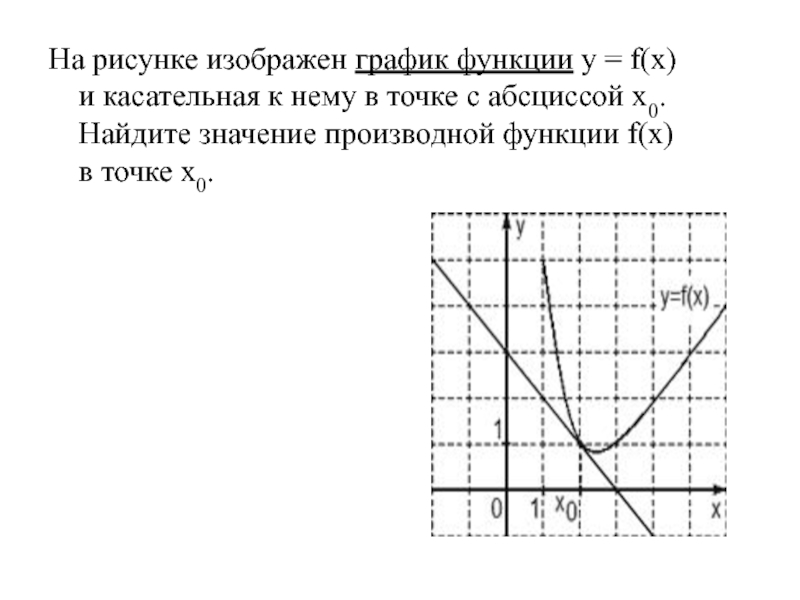
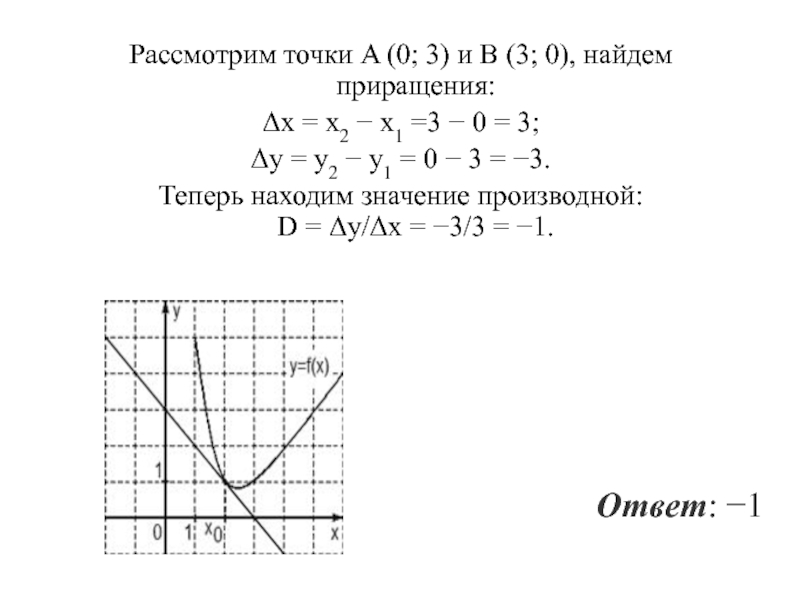
- 47. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- 48. Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:Δx = x2 − x1 =3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.Ответ: −1
- 49. На рисунке изображён график функцииy=f(x) и касательная
- 50. На рисунке изображён график функции
- 51. На рисунке изображён график функции y=f(x) и
- 52. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- 53. Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения: Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.Ответ: 0
- 54. Слайд 54
- 55. Слайд 55
- 56. На рисунке изображен график производнойфункции f(x),определенной
- 57. Слайд 57
- 58. Слайд 58
- 59. На рисунке изображен график функцииy=f(x),определенной на
- 60. На рисунке изображен график функцииy=f(x),определенной на интервале
- 61. На рисунке изображен график функцииy=f(x),определенной на интервале
- 62. На рисунке изображен график функцииy=f(x),определенной на интервале
- 63. На рисунке изображен график производнойфункции f(x),определенной
- 64. На рисунке изображен график производной функции f(x), определенной
- 65. Слайд 65
- 66. Прямая y=8x-5 параллельнакасательной к графику функцииy=x²+7x+7.Найдите абсциссу точки касания. Ответ: 0.5
- 67. Слайд 67
- 68. Прямая y=8x-9 является касательной к графику функции y=x³+x²+8x-9.Найдите абсциссу точки касания. Ответ: 0
- 69. Так как касательная параллельна прямой y =−2x−11 или совпадает
- 70. Прямая y=4x+8 параллельнакасательной к графику функцииy=x²-5x+7. Найдите абсциссу точки касания. Ответ: 4.5
- 71. Слайд 71
- 72. Слайд 72
- 73. Слайд 73
- 74. Слайд 74
- 75. Задачи с первообразной
- 76. Слайд 76
- 77. На рисунке изображён график функции y = F(x) —
- 78. На рисунке изображён график некоторой функции .
- 79. На рисунке изображён график некоторой функции .
- 80. И.В. Фельдман, репетитор по математике.Видеолекция 11. «Производная.
- 81. Скачать презентанцию
«Бугорки и впадины»
Слайды и текст этой презентации
Слайд 1Задачи типа В 8
на ЕГЭ
по математике
Филиппова Оксана Николаевна,
Моу Лицей, учитель
математики
Слайд 8Перечертить график производной, убрав всю лишнюю информацию. Отмечаем на координатной оси
нули производной — и все.
2. Выяснить знаки производной на промежутках между нулями. Если
для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.3. Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума.
Слайд 9На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума
функции f(x) на этом отрезке.
![На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.](/img/thumbs/4cc4ebcd4e2d9d6cc904605b507afcf9-800x.jpg)
Слайд 10Избавимся от лишней информации — оставим только границы [−5; 5]
и нули производной x = −3
и x = 2,5.
Также отметим знаки:
Ответ: −3
![Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:Ответ: −3](/img/thumbs/3da33cbef7fd817ce183e52ce34a7a68-800x.jpg)
Слайд 11На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума
функции f(x)
на этом отрезке.
![На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.](/img/thumbs/a695050d0bb4d56600734a381e0665fe-800x.jpg)
Слайд 12Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной
x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Ответ: 5
![Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной.](/img/thumbs/9a93d1ff7ac85d7d109fb8e4dcdf97d6-800x.jpg)
Слайд 13На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите
количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
![На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].](/img/thumbs/2442cf182734d3b70035a50203227e2f-800x.jpg)
Слайд 14Строим новый график, на котором отмечаем только границы [−4; 3] и нули
производной внутри него, точки x = −3,5 и x = 2. На этом графике есть лишь
одна точка максимума x = 2.Ответ: 1
![Строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него, точки x = −3,5 и x = 2.](/img/thumbs/5c7b6b56c1b7e36168f510d1bf611ae0-800x.jpg)
Слайд 152)На рисунке изображен график производной
функции f(x),определенной на интервале (-5;5).
Найдите количество
точек экстремума функции
f(x) на отрезке [-4;4].
Ответ: 3
![2)На рисунке изображен график производнойфункции f(x),определенной на интервале (-5;5).Найдите количество точек экстремума функцииf(x) на отрезке [-4;4]. Ответ:](/img/thumbs/97df76b8f08561992a82e29dfee7f3dc-800x.jpg)
Слайд 16На рисунке изображен график производной
функции f(x),определенной на интервале (-9;8).
Найдите точку
экстремума функции f(x) на ин-
тервале (-3;3).
Ответ: -2
Слайд 18Алгоритм:
1. Убрать всю лишнюю информацию. На исходном графике производной нас интересуют
в первую очередь нули функции, оставляем только их.
2. Отметить знаки производной на интервалах
между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает.( Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.)3. Вычислить требуемую в задаче величину.
Слайд 19На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания
функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
![На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих](/img/thumbs/8efb4d26af61d319c97424def14e7f66-800x.jpg)
Слайд 201. Перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5
и x = 5,3. 2. Отметим знаки производной. 3. Так как на интервале (− 1,5)
производная отрицательна, это и есть интервал убывания функции. 4. Осталось просуммировать все целые числа, которые находятся внутри этого интервала: −1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.Ответ: 14
![1. Перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. 2. Отметим знаки производной.](/img/thumbs/15517accdb35749dce71a961925dbf74-800x.jpg)
Слайд 21На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания
функции f(x). В ответе укажите длину наибольшего из них.
![На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.](/img/thumbs/b1360f422d89cffb256722d372e634f2-800x.jpg)
Слайд 221. Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых
в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. 2. Отметим знаки
производной и получим следующую картинку: Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). 3. Вычислим их длины: l1 = − 6 − (−8) = 2; l2 = 2 − (−3) = 5.Ответ: 5
![1. Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3](/img/thumbs/badd57b15a00e7a416c3cbc216fd3812-800x.jpg)
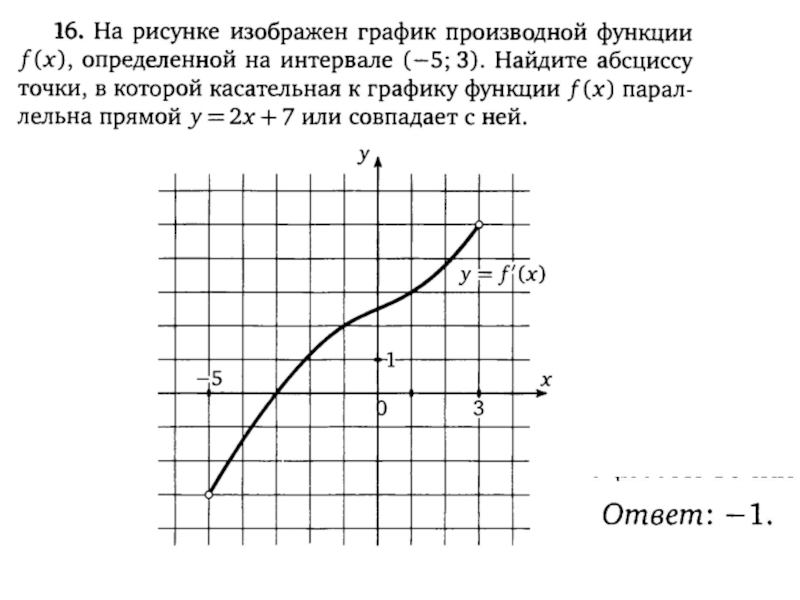
Слайд 23На рисунке изображен график производной функции
f(x), определенной на интервале (-8;3).
Найдите проме-
жутки возрастания функции f(x). В ответе укажите сумму целых
точек, входящих в эти промежутки.Ответ: -19
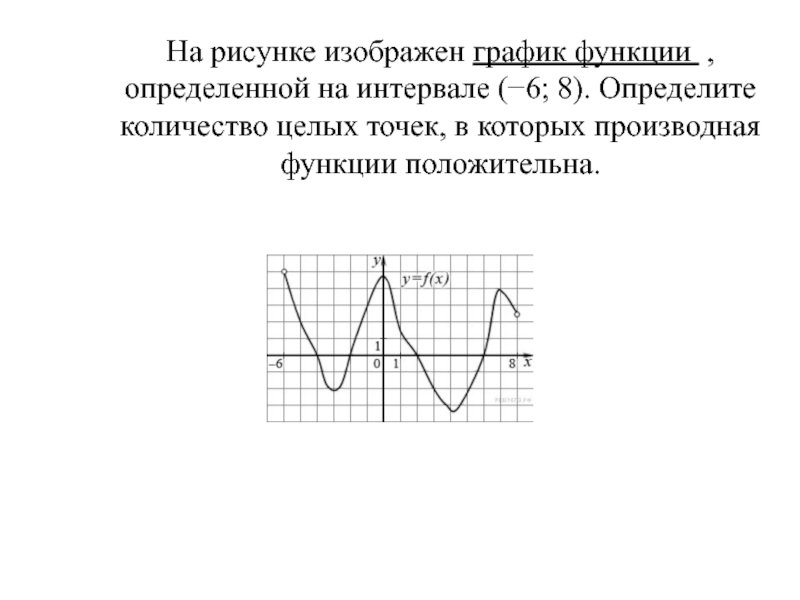
Слайд 24На рисунке изображен график функции , определенной на интервале (−6;
8). Определите количество целых точек, в которых производная функции положительна.
Слайд 25Производная функции положительна на тех интервалах, на которых функция возрастает,
т. е. на интервалах
(−3; 0) и (4,2; 7).
В них содержатся
целые точки −2, −1, 5 и 6, всего их 4.Ответ: 4.
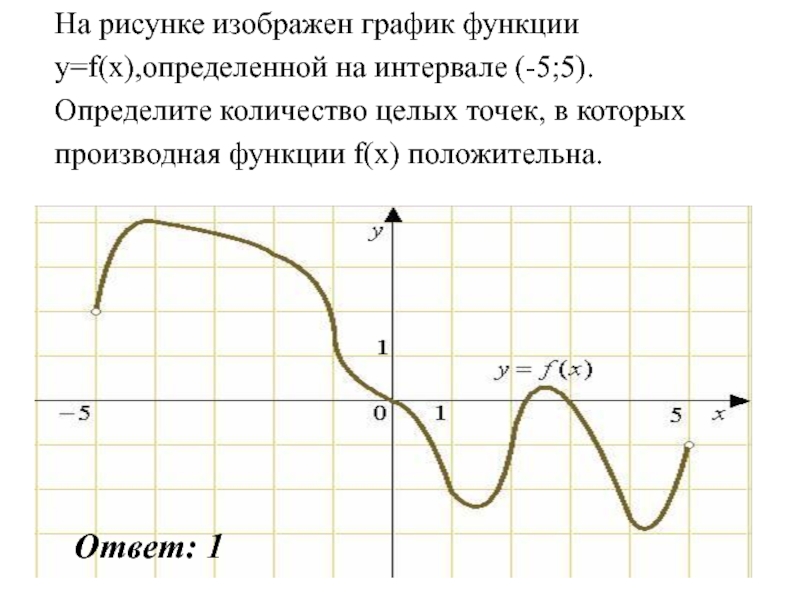
Слайд 26На рисунке изображен график функции
y=f(x),определенной на интервале (-5;5).
Определите количество
целых точек, в которых
производная функции f(x) положительна.
Ответ: 1
Слайд 27На рисунке изображён график дифференцируемой функции . На оси абсцисс
отмечены девять точек: . Среди этих точек найдите все точки,
в которых производная функции отрицательна. В ответе укажите количество найденных точек.Ответ: 3
Слайд 28 На рисунке изображен график производной
функции f(x),определенной на интервале(-11;3).
Найдите промежутки
возрастания функции f(x).
В ответе укажите длину наибольшего из них.
Ответ:
4
Слайд 29На рисунке изображен график производной
функции f(x),определенной на интервале(-6;12).
Найдите промежутки возрастания
функции f(x).
В ответе укажите длину наибольшего из них.
Ответ: 3
Слайд 30На рисунке изображен график производной функции f(x),определенной на интервале (-6;6).
Найдите промежутки возрастания функции f(x).
В ответе укажите сумму целых
точек, входящих в эти промежутки.Ответ: 9
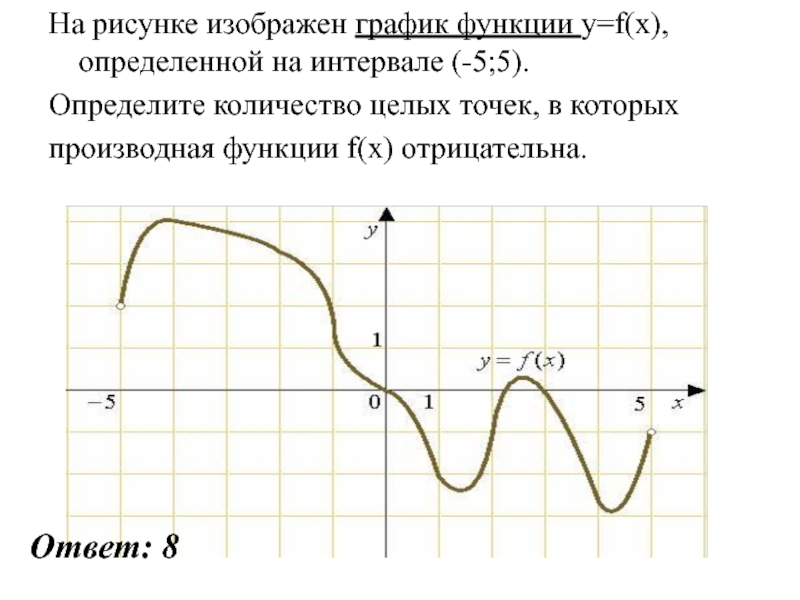
Слайд 31На рисунке изображен график функции y=f(x),определенной на интервале (-5;5).
Определите количество
целых точек, в которых
производная функции f(x) отрицательна.
Ответ: 8
Слайд 33На рисунке изображен график производной
функции f(x),определенной на интервале (-5;5).
В какой
точке отрезка [-4;-1] f(x) принимает
наибольшее значение.
Ответ: -1
![На рисунке изображен график производнойфункции f(x),определенной на интервале (-5;5).В какой точке отрезка [-4;-1] f(x) принимаетнаибольшее значение. Ответ:](/img/thumbs/ddfc670334e56edd166597800cf1bbfd-800x.jpg)
Слайд 34На рисунке изображен график производной
функции f(x),определенной на интервале
(-9;8). В
какой точке отрезка [0;6] f(x) принимает
наибольшее значение.
Ответ: 6
![На рисунке изображен график производнойфункции f(x),определенной на интервале (-9;8). В какой точке отрезка [0;6] f(x) принимаетнаибольшее значение.Ответ:](/img/thumbs/63b817bdffc86f187ec115814f1970c8-800x.jpg)
Слайд 35На рисунке изображен график производной
функции f(x),определенной на интервале (-9;8).
В какой
точке отрезка [-8;-4] f(x) принимает
наименьшее значение.
Ответ: -4
![На рисунке изображен график производнойфункции f(x),определенной на интервале (-9;8).В какой точке отрезка [-8;-4] f(x) принимаетнаименьшее значение.](/img/thumbs/0a05835f0be9e2f813195564f7b4432e-800x.jpg)
Слайд 36На рисунке изображен график производной
функции f(x),определенной на интервале (-6;6).
В какой
точке отрезка [-4;0] f(x) принимает
наименьшее значение.
Ответ: 0
![На рисунке изображен график производнойфункции f(x),определенной на интервале (-6;6).В какой точке отрезка [-4;0] f(x) принимаетнаименьшее значение.](/img/thumbs/e470d63d7e9b931649491c87a2d615d4-800x.jpg)
Слайд 37На рисунке изображен график производной
функции f(x),определенной на интервале (-9;8).
В какой
точке отрезка [-7;-3] f(x) принимает
наибольшее значение.
Ответ: -7
![На рисунке изображен график производнойфункции f(x),определенной на интервале (-9;8).В какой точке отрезка [-7;-3] f(x) принимаетнаибольшее значение.](/img/thumbs/ee42e25434113e8066ebce7da134d92d-800x.jpg)
Слайд 38На рисунке изображен график производной
функции f(x),определенной на интервале (-9;8).
В какой
точке отрезка [1;7] f(x) принимает
наименьшее значение.
Ответ: 1
![На рисунке изображен график производнойфункции f(x),определенной на интервале (-9;8).В какой точке отрезка [1;7] f(x) принимает наименьшее значение.](/img/thumbs/91e3641f125198dce365548230b8f28c-800x.jpg)
Слайд 39На рисунке изображен график производной
функции f(x),определенной на интервале (-6;6).
В какой
точке отрезка [-3;3] f(x) принимает
наименьшее значение.
Ответ: 2
![На рисунке изображен график производнойфункции f(x),определенной на интервале (-6;6).В какой точке отрезка [-3;3] f(x) принимает наименьшее значение.](/img/thumbs/4bc328e9b493b0c5ef6a26a4f0f0fa6f-800x.jpg)
Слайд 40На рисунке изображен график производной
функции f(x),определенной на интервале (-6;6).
В какой
точке отрезка [3;5] f(x) принимает
наибольшее значение.
Ответ: 5
![На рисунке изображен график производнойфункции f(x),определенной на интервале (-6;6).В какой точке отрезка [3;5] f(x) принимает наибольшее значение.Ответ:](/img/thumbs/c49c469e986cfb94eefb01c02de4935c-800x.jpg)
Слайд 44Алгоритм:
Метод двух точек
Если в задаче дан
график функции f(x). 1. Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
2. Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
3. Наконец, находим значение производной D = Δy/Δx. И это будет ответ.
Точки A и B надо искать именно на касательной, а не на графике функции f(x). Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Слайд 45На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение
производной функции f(x) в точке x0.
Слайд 46Рассмотрим точки A (−3; 2) и B (−1; 6)
и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2;
Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение
производной: D = Δy/Δx = 4/2 = 2.
Ответ: 2
Слайд 47На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение
производной функции f(x) в точке x0.
Слайд 48Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 =3 − 0 = 3;
Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение
производной: D = Δy/Δx = −3/3 = −1.
Ответ: −1
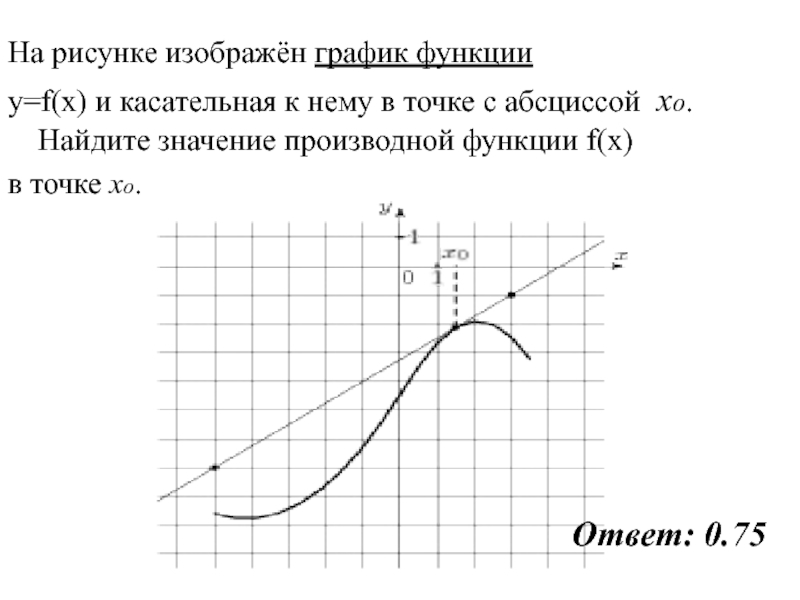
Слайд 49На рисунке изображён график функции
y=f(x) и касательная к нему в
точке с абсциссой xо. Найдите значение производной функции f(x)
в точке
xо.Ответ: 0.75
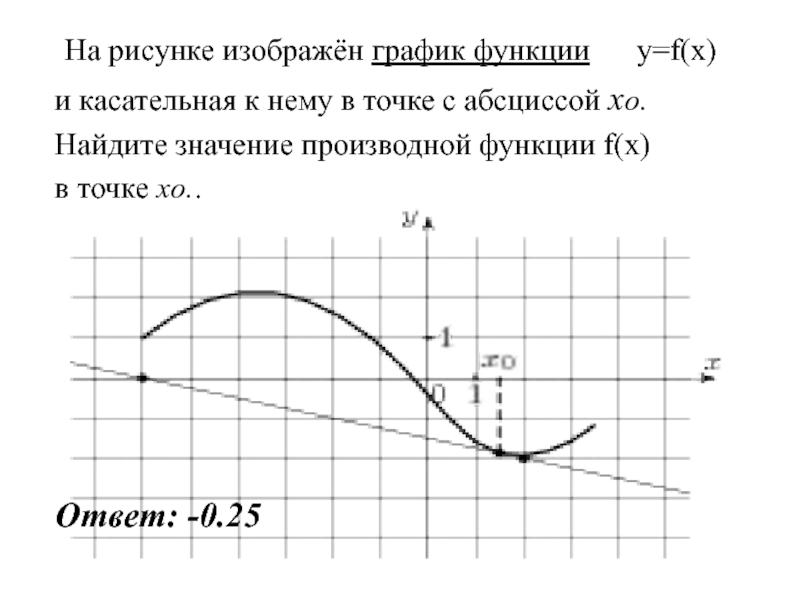
Слайд 50 На рисунке изображён график функции y=f(x)
и
касательная к нему в точке с абсциссой xo.
Найдите значение производной
функции f(x)в точке xo..
Ответ: -0.25
Слайд 51На рисунке изображён график функции y=f(x) и касательная к нему
в точке с
абсциссой xo. Найдите значение производной функции f(x) в
точке xo.Ответ: 0.5
Слайд 52На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение
производной функции f(x) в точке x0.
Слайд 53Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5;
Δy = y2 − y1 = 2 − 2 = 0.
Осталось
найти значение производной: D = Δy/Δx = 0/5 = 0.
Ответ: 0
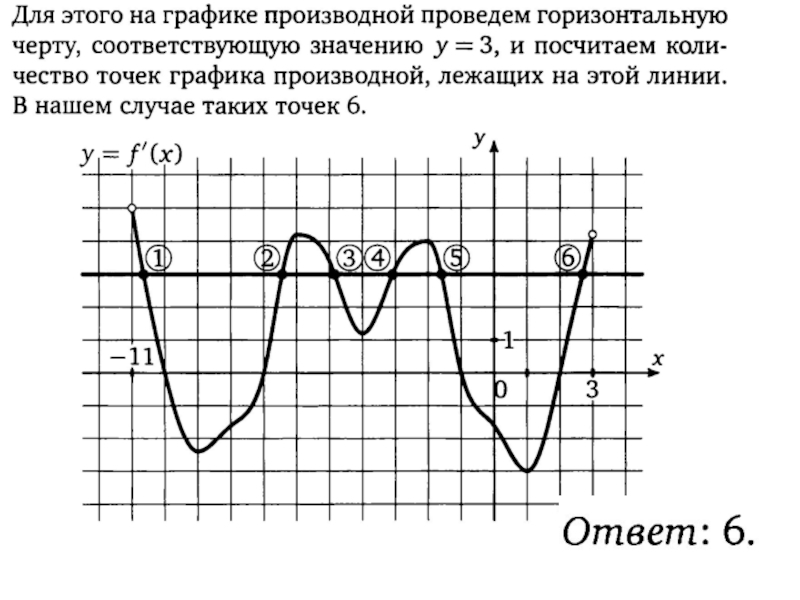
Слайд 56 На рисунке изображен график производной
функции f(x),определенной на интервале (-6;6).
Найдите
количество точек, в которых касательная
к графику функции f(x) параллельна
прямойy=-2x+4 или совпадает с ней.
Ответ: 4
Слайд 59 На рисунке изображен график функции
y=f(x),определенной на интервале (-11;2).
Найдите количество
точек, в которых касательная к
графику функции параллельна прямой y=-6.
Ответ: 7 (бугорки и впадины)
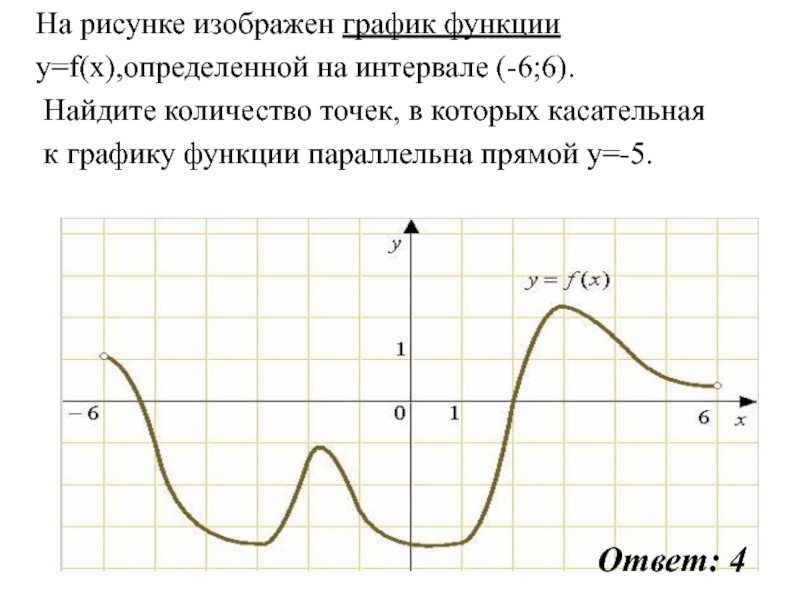
Слайд 60На рисунке изображен график функции
y=f(x),определенной на интервале (-6;6).
Найдите количество
точек, в которых касательная
к графику функции параллельна прямой y=-5.
Ответ: 4
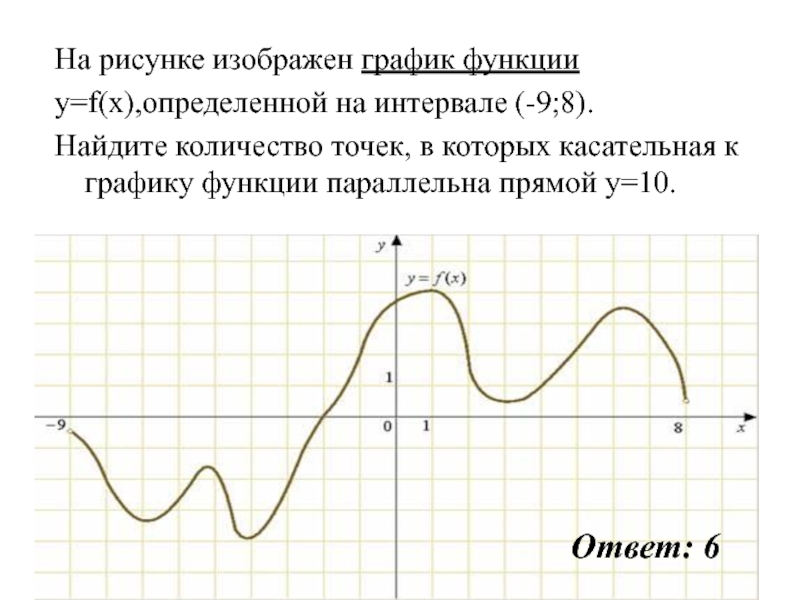
Слайд 61На рисунке изображен график функции
y=f(x),определенной на интервале (-9;8).
Найдите количество
точек, в которых касательная к графику функции параллельна прямой y=10.
Ответ: 6
Слайд 62На рисунке изображен график функции
y=f(x),определенной на интервале (-5;5).
Найдите количество точек,
в которых касательная к
графику функции параллельна прямой y=6.
Ответ: 4
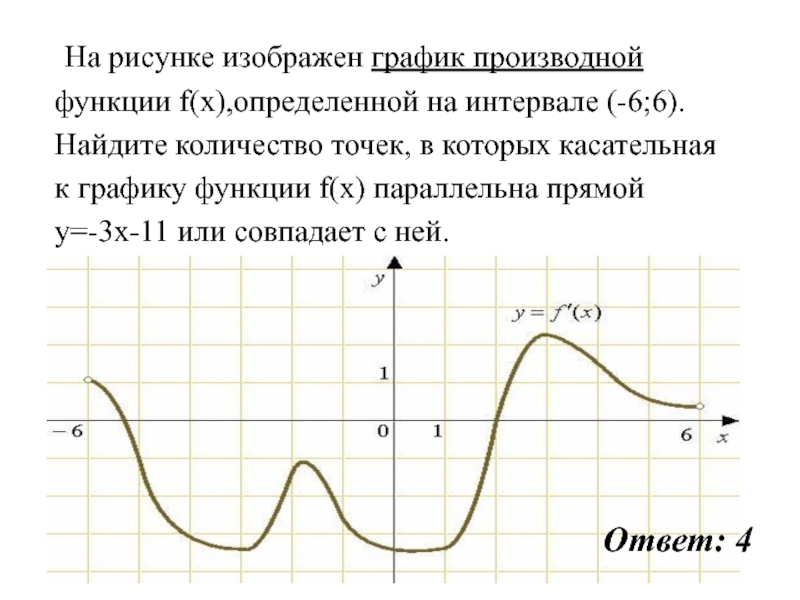
Слайд 63 На рисунке изображен график производной
функции f(x),определенной на интервале (-6;6).
Найдите
количество точек, в которых касательная
к графику функции f(x) параллельна
прямойy=-3x-11 или совпадает с ней.
Ответ: 4
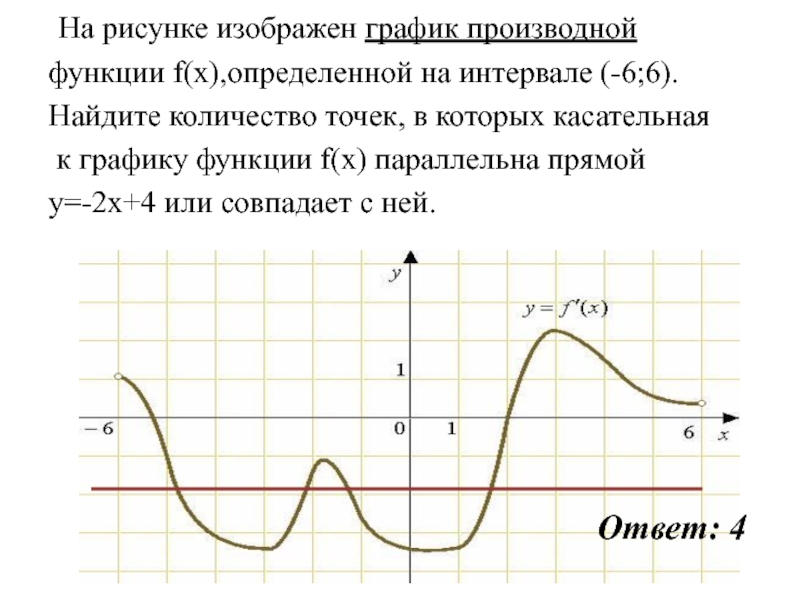
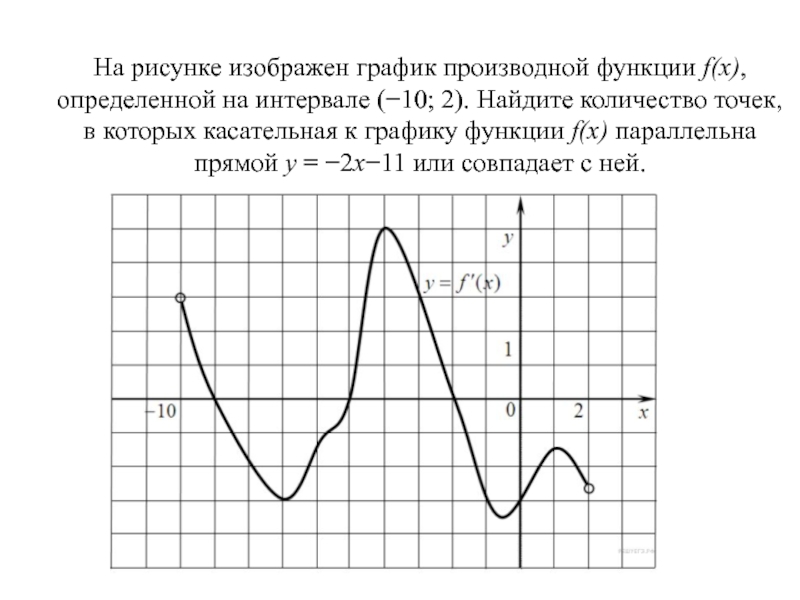
Слайд 64На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2).
Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x−11
или совпадает с ней.
Слайд 66
Прямая y=8x-5 параллельна
касательной к графику функции
y=x²+7x+7.
Найдите абсциссу точки касания.
Ответ:
0.5
Слайд 68
Прямая y=8x-9 является касательной к графику функции y=x³+x²+8x-9.
Найдите абсциссу точки
касания.
Ответ: 0
Слайд 69Так как касательная параллельна прямой y =−2x−11 или совпадает с ней, их
угловые коэффициенты равны –2. Найдем количество точек, в которых y'(x0) = −2, геометрически
это соответствует количеству точек пересечения графика производной с прямой y= −2. На данном интервале таких точек 5.Ответ: 5.
Слайд 70
Прямая y=4x+8 параллельна
касательной к графику функции
y=x²-5x+7.
Найдите абсциссу точки касания.
Ответ: 4.5
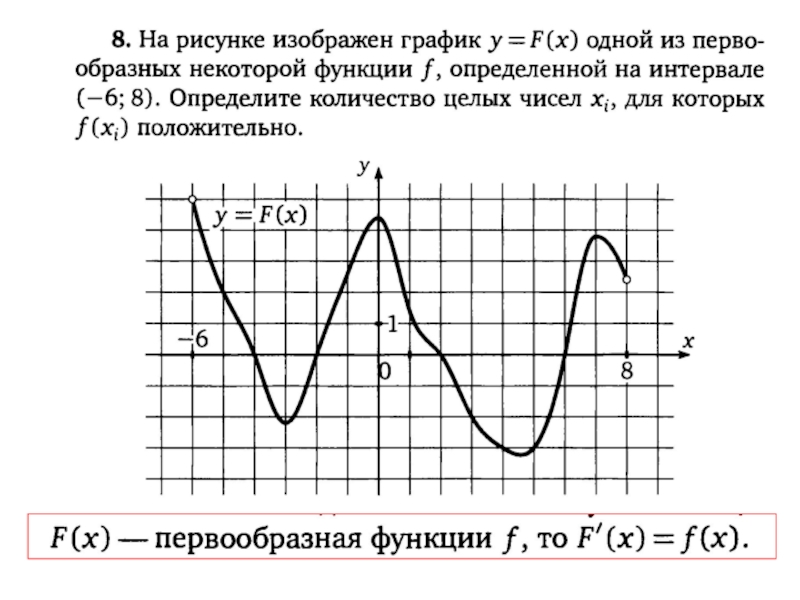
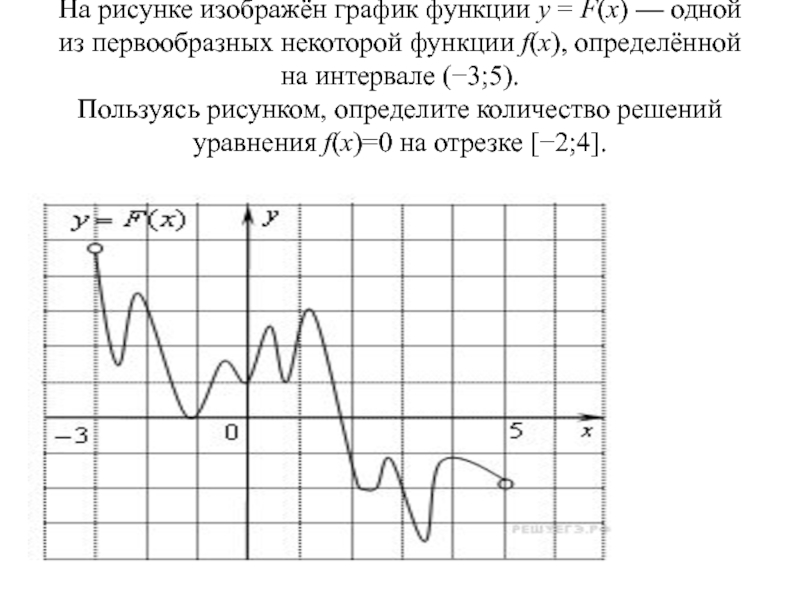
Слайд 77На рисунке изображён график функции y = F(x) — одной из первообразных
некоторой функции f(x), определённой на интервале (−3;5). Пользуясь рисунком, определите
количество решений уравнения f(x)=0 на отрезке [−2;4].
Слайд 78На рисунке изображён график некоторой функции . Функция
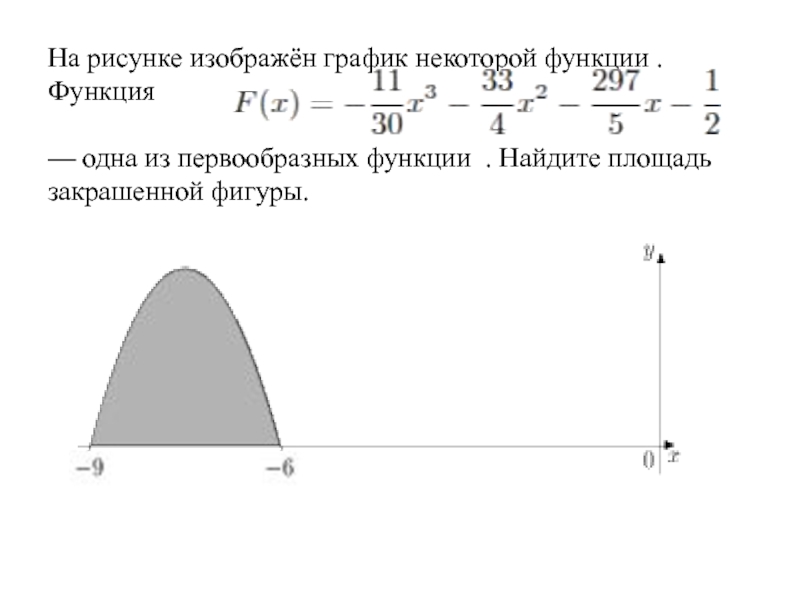
— одна из первообразных функции . Найдите
площадь закрашенной фигуры.
Слайд 79На рисунке изображён график некоторой функции . Функция — одна
из первообразных функции . Найдите площадь закрашенной фигуры.
Слайд 80И.В. Фельдман, репетитор по математике.
Видеолекция 11. «Производная. Касательная. Применение производной
к исследованию функции. Задание В8″
Геометрический смысл производной. Уравнение касательной к
графику функции. Задание В8Производная. Физический смысл производной. Задание В8
Абсцисса точки касания. Задание В8
Определенный интеграл. Площадь криволинейной трапеции. Формула Ньютона-Лейбница. Задание В8
http://uztest.ru
http://www.egehelp.ru
http://www.mathege.ru
http://www.matematika
http://webmath.exponenta
http://www.math.com.ua/mathdir
http://www.ctege.org
www.fipi.ru
www.mioo.ru
