закон распределения случайной дискретной величины

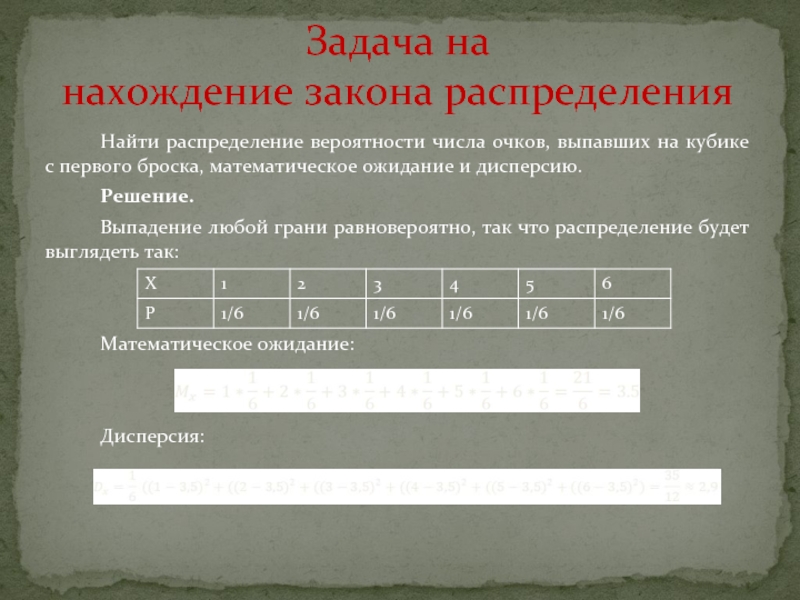
опыта, причем вероятность каждого исхода различна.

Случайная величина называется дискретной,

если в пределах одного опыта, количество значений которые она может принимать, конечно.

Понятие дискретной
случайной величины

вероятностями их появления. Закон распределения можно задать таблично, аналитически (в

виде формулы Бернулли) и графически (в виде многоугольника распределения).
Табличное задание закона распределения:


Здесь х1, х2, x3,...,хn — значения, которые может принять случайная дискретная величина X и их вероятности  p1=Р(Х=х1),  p2=Р(Х=х2), p3=Р(Х=х3), p4=Р(Х=х4), pn=Р(Х = хn) и p1+p2+p3+p4+...+pn=1.

Закон распределения случайной величины

A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого

числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу.
Испытание называется независимым от события А если вероятность появления события А в каждом испытании не зависит от результатов проведения испытаний.


где n – количество независимых испытаний;
p – вероятность наступления события А;
q – вероятность того, что событие А не произойдет, q = 1 – p;
m – количество раз, когда событие А не произошло при n различных испытаний (m < n).

Формула Бернулли

распределения вероятностей случайной величины. Для случайной величины X, принимающей последовательность

значений x1, x2, ..., xn, с вероятностями, равными соответственно p1, p2, ..., pn, математическое ожидание определяется формулой:




где k – количество независимых испытаний;
– значение случайной дискретной величины;
– вероятность значения случайной дискретной величины;

Понятие математического ожидания

теории вероятностей - мера рассеивания (отклонения от среднего). В статистике

дисперсия есть среднее арифметическое из квадратов отклонений наблюденных значений (x1, x2,...,xn) случайной величины от их среднего арифметического. В теории вероятностей дисперсия случайной величины Х называется математическое ожидание Е (Х — mх)2 квадрата отклонения Х от её математического ожидания mх= Е (Х). Дисперсия случайной величины Х обозначается через D (X) или через s2X.

Понятие дисперсии

броска, математическое ожидание и дисперсию.
Решение.
Выпадение любой грани равновероятно, так что

распределение будет выглядеть так:


Математическое ожидание:


Дисперсия:

Задача на нахождение закона распределения