Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы логики. Алгебра высказываний. Логические выражения
Содержание
- 1. Основы логики. Алгебра высказываний. Логические выражения
- 2. Историческая справкаОсновы формальной логики заложил Аристотель (
- 3. Логика – это наука о формах и
- 4. В основе логических схем и устройств ПК
- 5. Основные формы мышления Основными формами мышления являются: ПОНЯТИЯ,
- 6. УМОЗАКЛЮЧЕНИЕ – это форма мышления, посредством которой
- 7. Высказывание – повествовательное предложение, в котором что-либо
- 8. Алгебра высказыванийПростым высказываниям ставятся в соответствие логические
- 9. Логическое отрицание (инверсия)Присоединение частицы «не» к высказыванию.Делает
- 10. Логическое умножение (конъюнкция)Объединение двух (или нескольких) высказываний
- 11. Логическое сложение (дизъюнкция)Объединение двух (или нескольких) высказываний
- 12. Импликация (логическое следование)Соответствующие выражения языка: Если
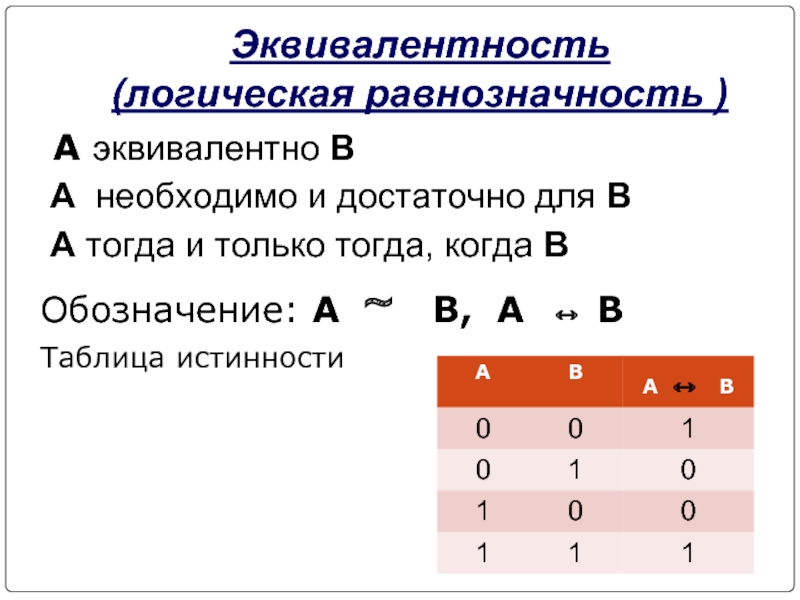
- 13. Эквивалентность (логическая равнозначность ) A эквивалентно
- 14. Таблицы истинностиДля каждого составного высказывания (логического выражения)
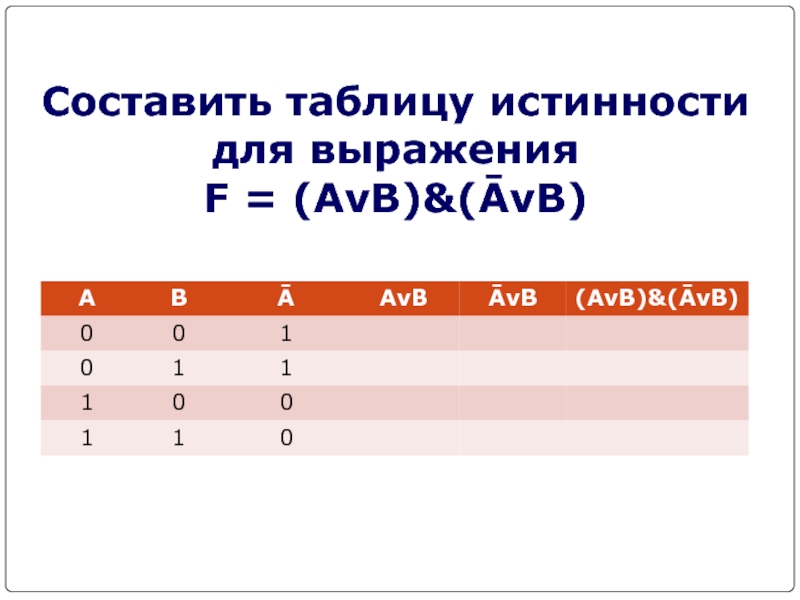
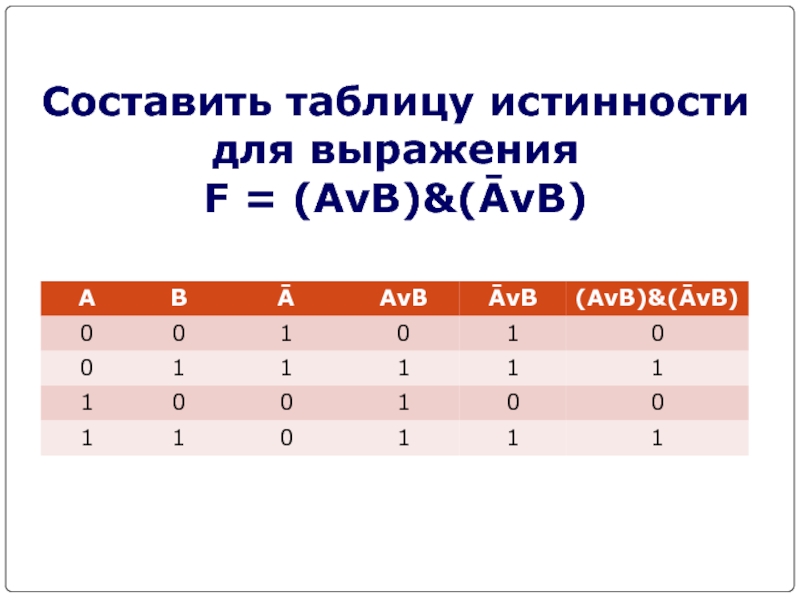
- 15. Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
- 16. F = (AvB)&(ĀvB) Количество входных переменных
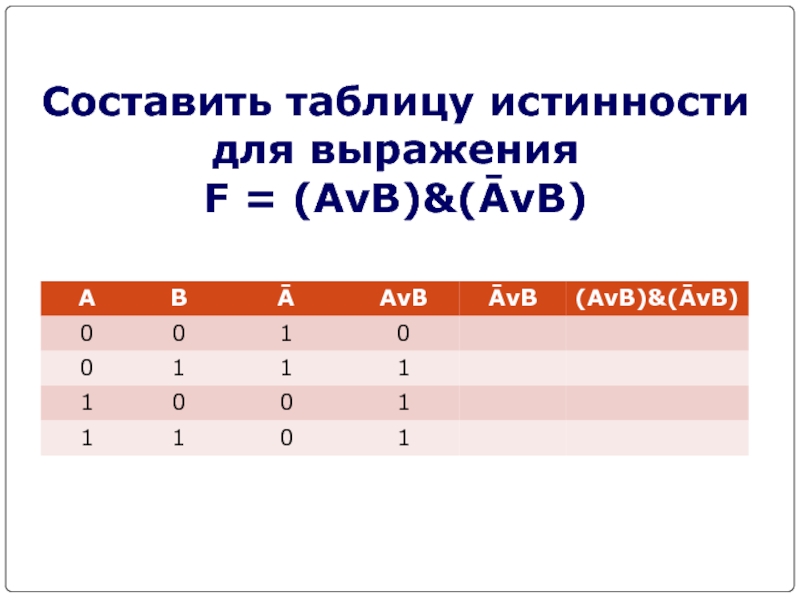
- 17. Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
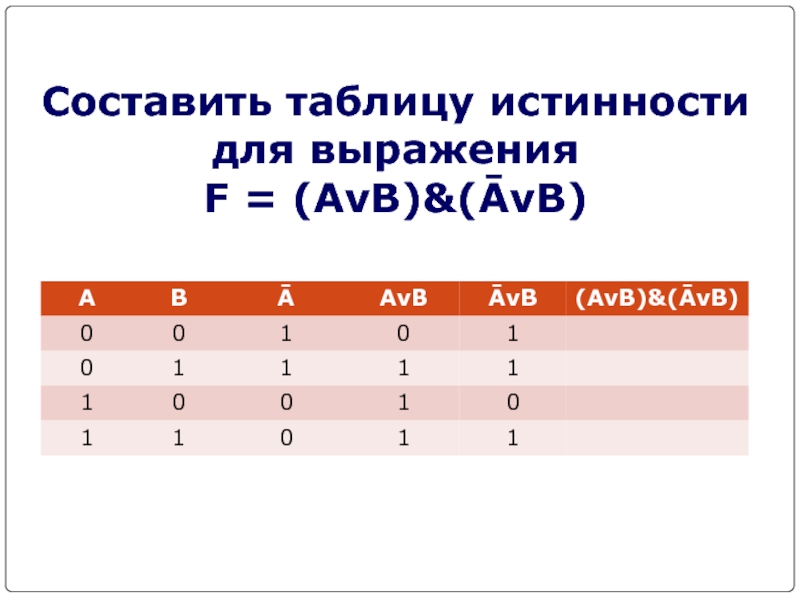
- 18. Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
- 19. Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
- 20. Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
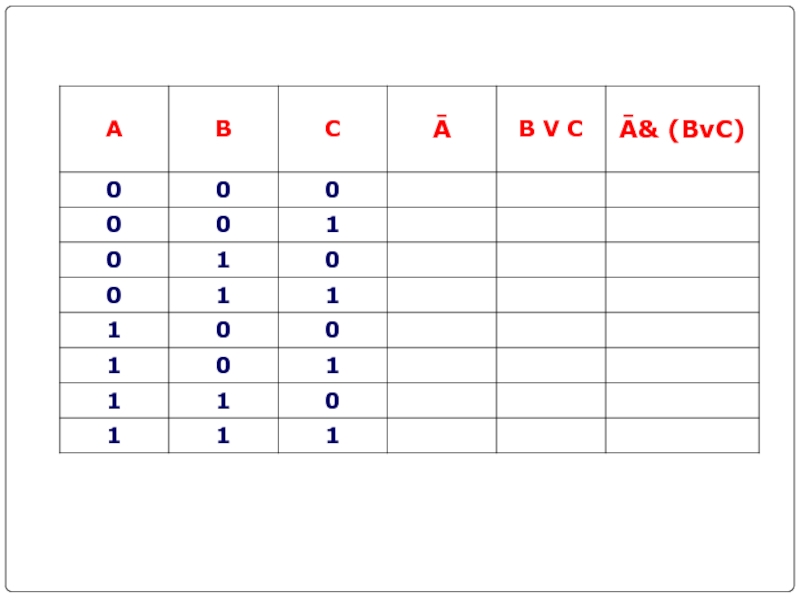
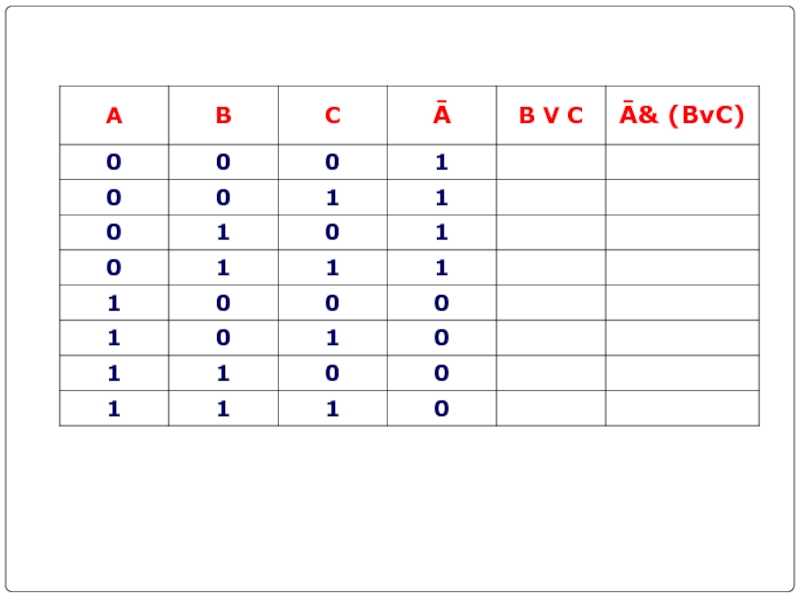
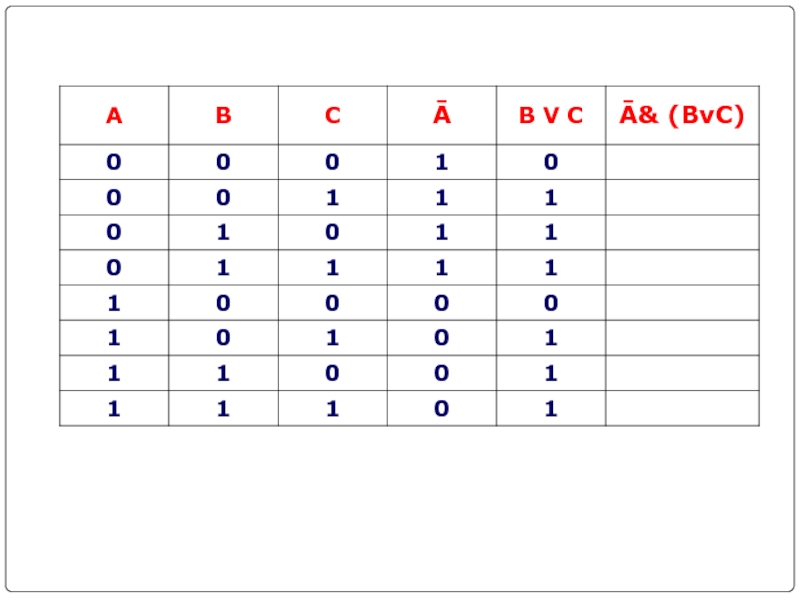
- 21. Составить таблицу истинности для логической функции:1. Количество
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
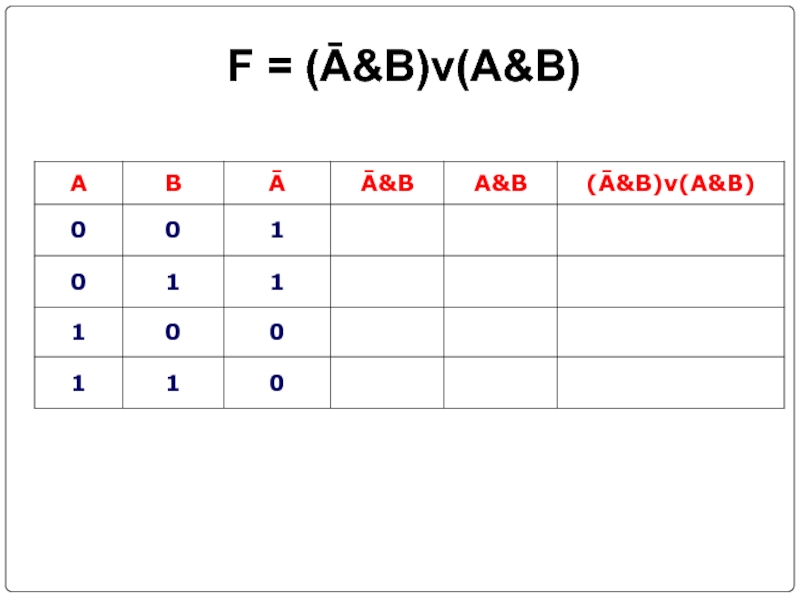
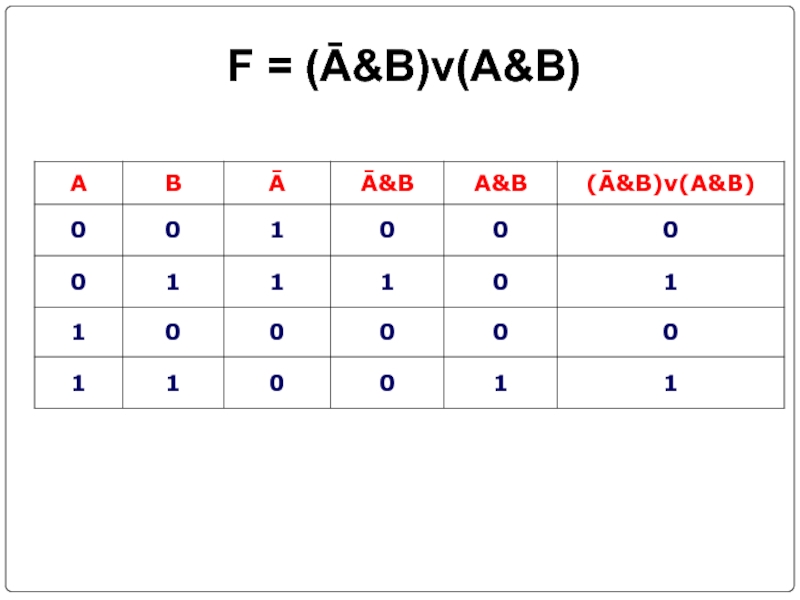
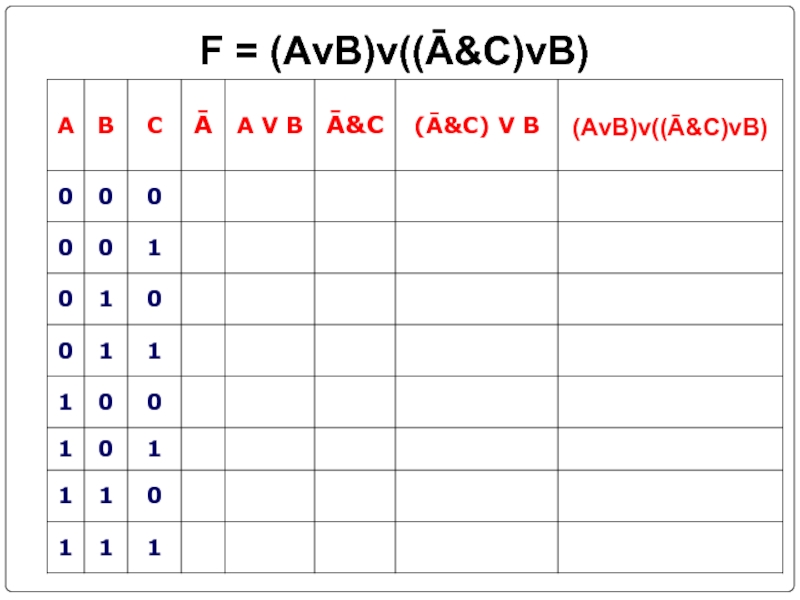
- 26. Составить таблицы истинности F = (Ā&B)v(A&B) F = (AvB)v((Ā&C)vB) F= (A&C ) → (( AvB)↔C)
- 27. F = (Ā&B)v(A&B)
- 28. F = (Ā&B)v(A&B)
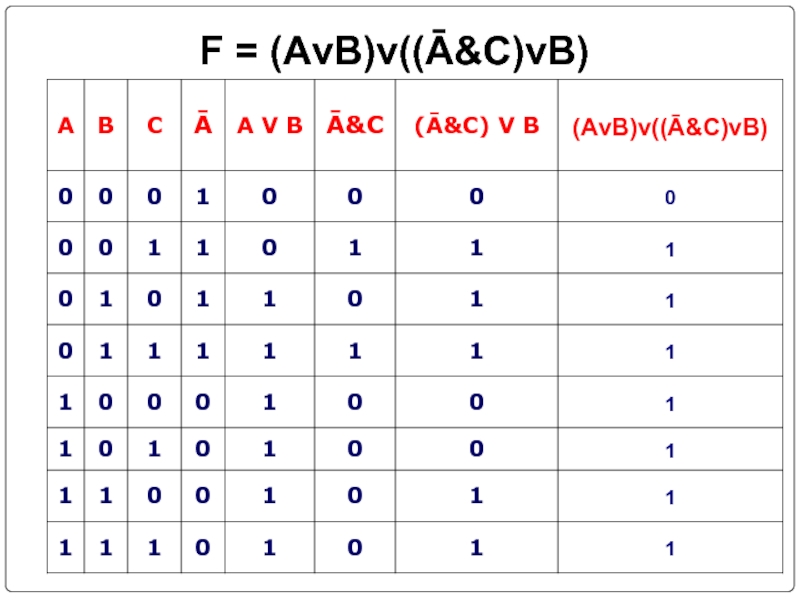
- 29. F = (AvB)v((Ā&C)vB)
- 30. F = (AvB)v((Ā&C)vB)
- 31. Скачать презентанцию
Историческая справкаОсновы формальной логики заложил Аристотель ( 384 -322 гг. до н.э.). Ввел основные формы абстрактного мышления.
Слайды и текст этой презентации
Слайд 3Логика – это наука о формах и способах мышления.
Логика
изучает мышление как средство познания объективного мира. Законы логики отражают
в сознании человека свойства, связи и отношения объектов окружающего мира.Формальная логика связана с анализом наших обычных содержательных умозаключений, выражаемых разговорным языком. Математическая логика изучает только умозаключения со строго определенными объектами и суждениями, для которых можно однозначно решить, истинны они или ложны.
ФОРМЫ МЫШЛЕНИЯ
Слайд 4В основе логических схем и устройств ПК лежит специальный математический
аппарат, использующий законы логики.
Математическая логика изучает вопросы применения
математических методов для решения логических задач и построения логических схем.3. Знание логики необходимо при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции.
Слайд 5Основные формы мышления
Основными формами мышления являются:
ПОНЯТИЯ, ВЫСКАЗЫВАНИЯ, УМОЗАКЛЮЧЕНИЯ.
ПОНЯТИЕ- форма
мышления, в которой отражаются существенные признаки отдельного объекта или класса
однородных объектов.Понятие имеет две стороны: содержание и объем.
Содержание понятия составляет совокупность существенных признаков объекта. Чтобы раскрыть содержание понятия, следует найти признаки, необходимые и достаточные для выделения данного объекта из множества других объектов. Например, содержание понятия «персональный компьютер» можно раскрыть следующим образом: «Персональный компьютер — это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя».
Объем понятия определяется совокупностью предметов, на которую оно распространяется. Объем понятия «персональный компьютер» выражает всю совокупность (сотни миллионов) существующих в настоящее время в мире персональных компьютеров.
Слайд 6
УМОЗАКЛЮЧЕНИЕ – это форма мышления, посредством которой из одного или
нескольких истинных суждений, называемых посылками, мы по определенным правилам вывода
получаем новое суждение (заключение).Например,
Все металлы - простые вещества.
Литий - металл.→ Литий - простое вещество.
Например,
Один из углов треугольника равен 90º. → Этот треугольник прямоугольный.
Слайд 7Высказывание – повествовательное предложение, в котором что-либо утверждается или отрицается
о свойствах реальных объектах или отношениях между ними.
Например, 2*2=4;
Процессор- устройство обработки информации; Сегодня хорошая погода.
Составные высказывания – образуются из простых с помощью специальных слов (не, и, или).
Например: сегодня хорошая погода и светит солнце.
Слайд 8Алгебра высказываний
Простым высказываниям ставятся в соответствие логические переменные.
Пример:
А = «2
* 2 = 4» истинно А = 1
В = «3 *
3 = 5» ложно В = 0Логическая переменная может принимать лишь два значения: «истина» (1) или «ложь» (0).
Слайд 9Логическое отрицание (инверсия)
Присоединение частицы «не» к высказыванию.
Делает истинное высказывание ложным,
а ложное – истинным.
Обозначение: не А, Ā, ¬А.
Таблица истинности
Слайд 10Логическое умножение (конъюнкция)
Объединение двух (или нескольких) высказываний в одно с
помощью союза «и».
Обозначение: А и В, А&В.
Таблица истинности
Слайд 11Логическое сложение (дизъюнкция)
Объединение двух (или нескольких) высказываний в одно с
помощью союза «или».
Обозначение: А или В, АvВ
Таблица истинности
Слайд 12Импликация (логическое следование)
Соответствующие выражения языка:
Если A, то B
A достаточно для B
B следует из A
Обозначение:
А → ВТаблица истинности
Слайд 13Эквивалентность
(логическая равнозначность )
A эквивалентно B
A необходимо и
достаточно для B
A тогда и только тогда, когда B
Обозначение:
А ∼ В, А ↔ ВТаблица истинности
Слайд 14Таблицы истинности
Для каждого составного высказывания (логического выражения) можно построить таблицу
истинности, которая определяет истинность или ложность логического выражения при всех
возможных комбинациях исходных значений простых высказываний (логических переменных).При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий:
1) записать выражение и определить порядок выполнения операций
2) определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение (определяется по формуле Q =2n, где n - количество входных переменных)
3) определить количество столбцов в таблице истинности (= количество логических переменных + количество логических операций)
4) построить таблицу истинности, обозначить столбцы (имена переменных и обозначения логических операций в порядке их выполнения) и внести в таблицу возможные наборы значений исходных логических переменных.
5) заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности
Слайд 16F = (AvB)&(ĀvB)
Количество входных переменных в заданном выражении
равно двум (A,B). Значит, количество входных наборов, а значит и
строк Q=22=42. Количество столбцов равно 6 (2 переменные + 4 операции).
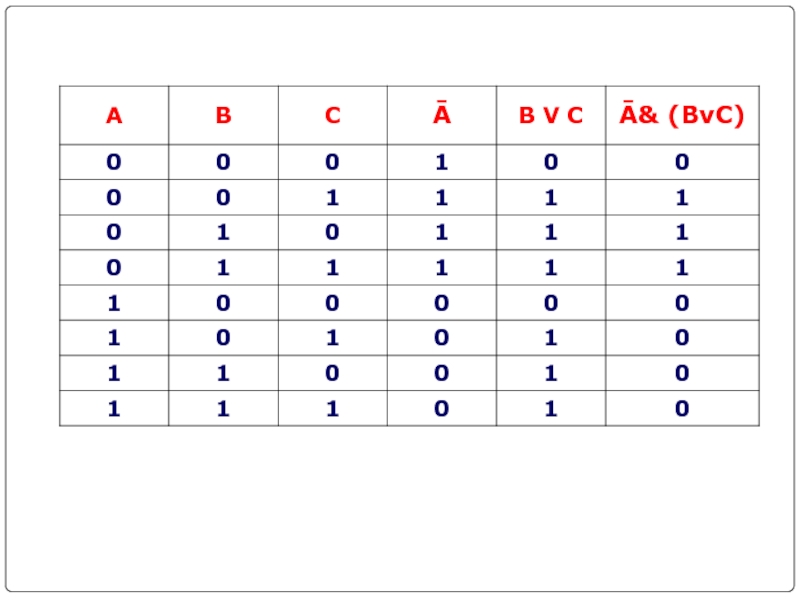
Слайд 21Составить таблицу истинности для логической функции:
1. Количество входных переменных в
заданном выражении равно трем (A,B,C). Значит, количество входных наборов, а
значит и строк Q=23=8.2. Количество столбцов равно 6 (3 переменные + 3 операции). Столбцы таблицы истинности соответствуют значениям исходных выражений A,B,C, промежуточных результатов Ā и (B V C), а также искомого окончательного значения сложного арифметического выражения Ā& (BvC)
F =Ā& (BvC)
Теги