Полуправильные и звездчатые многогранники. Кристаллы

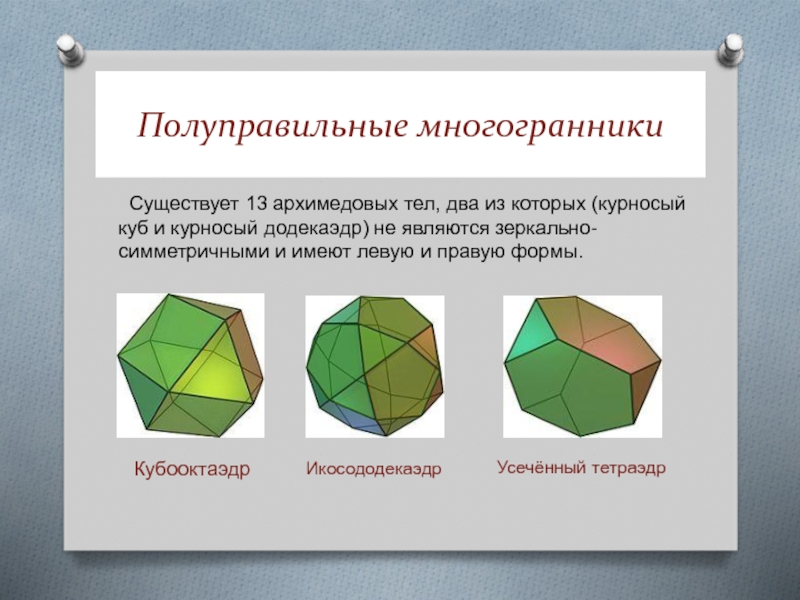
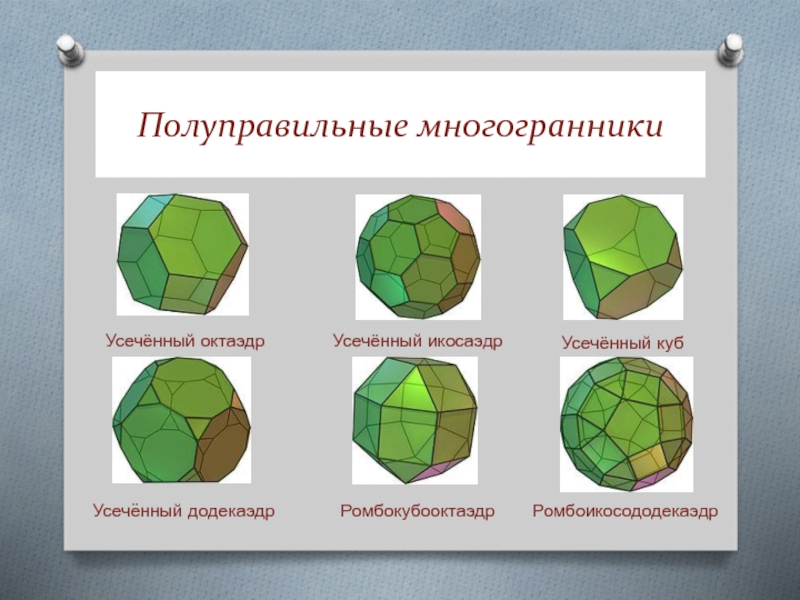
обладающие двумя свойствами:
Все грани являются правильными многоугольниками двух или более

типов (если все грани — правильные многоугольники одного типа, это — правильный многогранник);
Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую. В частности, все многогранные углы при вершинах конгруэнтны.

имеют конгруэнтные грани, равные двугранные углы и правильные многогранные углы.

Каталановы тела тоже иногда называют полуправильными многогранниками. В этом случае полуправильными многогранниками считается совокупность архимедовых и каталановых тел. Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани — правильные многоугольники, но они не одинаковы, а каталановы — в том смысле, что их грани одинаковы, но не являются правильными многоугольниками; при этом для тех и других сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического.
То есть, полуправильными в этом случае называются тела, у которых отсутствует только одно из первых двух из следующих свойств правильных тел:
Все грани являются правильными многоугольниками;
Все грани одинаковы;
Тело относится к одному из трёх существующих типов пространственной симметрии.

куб и курносый додекаэдр) не являются зеркально-симметричными и имеют левую

и правую формы.

Кубооктаэдр

Икосододекаэдр

Усечённый тетраэдр

которого пересекаются между собой. Как и у незвёздчатых многогранников грани

попарно соединяются в ребрах, при этом внутренние линии пересечения не считаются рёбрами.

Существует только одна звёздчатая форма октаэдра.

додекаэдр, большой звёздчатый додекаэдр

соединение икосаэдра и додекаэдра

симметричных многогранников, основанную на их внутренней структуре, то есть на

одном из нескольких определённых регулярных расположений составляющих вещество частиц (атомов, молекул, ионов).

кристалл
Является, по сути, математическим объектом, имеющим полную, свойственную ему симметрию,

идеализированно ровные гладкие грани.
Реальный кристалл
Всегда содержит различные дефекты внутренней структуры решетки, искажения и неровности на гранях и имеет пониженную симметрию многогранника вследствие специфики условий роста, неоднородности питающей среды, повреждений и деформаций. Реальный кристалл не обязательно обладает кристаллографическими гранями и правильной формой, но у него сохраняется главное свойство — закономерное положение атомов в кристаллической решётке.