Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразование выражений, содержащих операцию извлечения квадратного корня
Содержание
- 1. Преобразование выражений, содержащих операцию извлечения квадратного корня
- 2. Знание – самое превосходное из владений.
- 3. Цель урока:Повторить свойства квадратных корней; объяснить правила
- 4. План урока:Математическая разминкаРассмотреть правила вынесения множителя из-под
- 5. Повторим:Как называется выражение ?При
- 6. Вариант 11. Вычислить квадратный корень из заданных
- 7. Ответы:
- 8. Оценочная таблица
- 9. Используя эти формулы, можно выполнять
- 10. Пример 1. Упростить выражение:
- 11. а) =б)
- 12. Пример 3. Внести множитель под знак квадратного
- 13. Закрепление нового материала:Устно: № 15.1;
- 14. Предлагаю вам примеры для самостоятельного решения
- 15. Обучающая самостоятельная работаа)
- 16. Подведём итоги:
- 17. 1.пЧетверть, в которой расположен график функкции у= ? евряа
- 18. 1.2.рпевряаКаков вид графика квадратичной функции?пабалоа
- 19. 1.2.3.арпевряа3. Квадратный корень из 144?пабалоавдднеацть
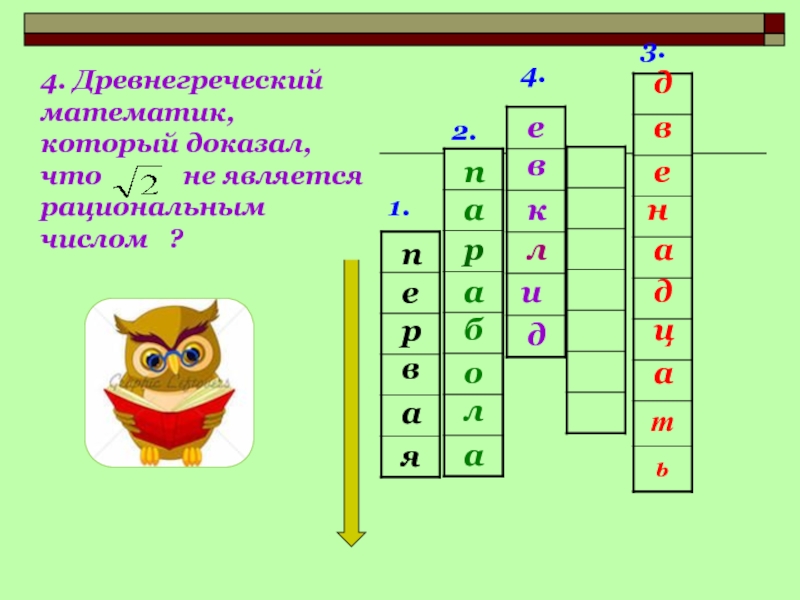
- 20. 1.2.3.4.алрпевряа4. Древнегреческий математик,который доказал, что не является рациональным числом ?пабалоавдднеацкведи
- 21. 1.2.3.4.5.арлрпевряа5. Арифметический корень?пабалоавдднеацкведидалаки
- 22. Дом. Задание: № 15.7; № 15.12;№ 15.15
- 23. Слайд 23
- 24. Скачать презентанцию
Знание – самое превосходное из владений. Все стремятся к нему, само оно не приходит. Абу Рейхан ал-Беруни04.09.973-9.12.1048 - великий ученый из Хорезмa
Слайды и текст этой презентации
Слайд 2Знание – самое превосходное из владений. Все стремятся к нему,
само оно не приходит. Абу Рейхан ал-Беруни
из Хорезмa
Слайд 3Цель урока:
Повторить свойства квадратных корней; объяснить правила вынесения множителя из-под
знака корня, внесения множителя под знак корня
Проверить знания и умения
с помощью обучающей самостоятельной работы
Слайд 4
План урока:
Математическая разминка
Рассмотреть правила вынесения множителя из-под знака корня, внесения
множителя под знак корня
Закрепление свойств квадратного корня на примерах
Самостоятельная работа
Подведение
итоговЗадание на дом
Слайд 5
Повторим:
Как называется выражение ?
При каком значении а
выражение имеет смысл?
В формулировках и записях свойств
арифметических корней заполните пропуски: а) корень из произведения неотрицательных множителей равен_____________корней из этих множителей;
б) корень из дроби, числитель которой неотрицателен, а знаменатель______, равен корню из числителя, делённому на _______;
Слайд 6Вариант 1
1. Вычислить квадратный корень из заданных выражений:
2. Найти корень
квадратный из произведения чисел 16 и 0,01.
3. Вычислить произведение корней
квадратных чисел 20 и 5.4. Вычислить квадратный корень разности квадратов 13 и 12.
Математическая разминка
Вариант 2
1. Вычислить квадратный корень из заданных выражений:
2. Найти квадратный корень из произведения чисел 25 и 0,0004.
3. Найти частное квадратных корней 192 и 75.
4. Вычислить квадратный корень разности квадратов 41 и 40.
Слайд 9 Используя эти формулы, можно выполнять различные преобразования выражений,
содержащих операцию извлечения квадратного корня.
Повторим свойства квадратных корней:
Слайд 10Пример 1. Упростить выражение:
а)
;б) .
Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения.
=
=
Слайд 13Закрепление нового материала:
Устно: № 15.1; 15.2.
№ 15.5 (а,б);
№ 15.8 (а,б);
№
15.10 (а,б); № 15.13 (а,б);
№ 15.16 (а,б);
№ 15.20 (а,б).
Слайд 15Обучающая самостоятельная работа
а) =
б)
=
в)
=г) =
д) =
е) =
а) =
б) =
в) =
г) =
д) =
е) =
1. Вынесите множитель из–под знака корня:
2. Внесите множитель под знак корня:
а) =
б) =
а) =
б) =
Слайд 201.
2.
3.
4.
а
л
р
п
е
в
р
я
а
4. Древнегреческий
математик,
который доказал,
что
не является
рациональным
числом ?
п
а
б
а
л
о
а
в
д
д
н
е
а
ц
к
в
е
д
и
Теги
