Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
В чем секрет словесных головоломок?
Содержание
- 1. В чем секрет словесных головоломок?
- 2. Объект исследования - анаграммы, палиндромы, метаграммы, абецедарии,
- 3. Поставленные задачи:- установить связь между математическими понятиями
- 4. ТЕХНЭ – литература, основанная на строгих формальных
- 5. В математике перестановкой из n элементов называется
- 6. Слайд 6
- 7. Параграмма - словосочетания, которое делятся на два
- 8. 2. Палиндром - это слово, которое одинаково
- 9. В случае, когда при обратном прочтении получается
- 10. Глава 2. Абецедарии, логогрифы, последовательности Абецедарий, или алфавитный
- 11. Арифметической прогрессией называется последовательность, каждый член которой,
- 12. Глава 3. Словесный магический квадрат Словесный магический
- 13. Словесный квадрат по своему строению очень похож
- 14. Палиндромы и абецедарии М. Цыганковой Палиндромы:Шалаш латал
- 15. Список литературыКвятковский А. Поэтический словарь. М., 1966.Литературный
- 16. Спасибо за внимание
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема научной работы:
«В чем секрет словесных головоломок?»
Автор работы:
Цыганкова Мария
ученица 8
«А» класса
Анна ЕвгеньевнаСлайд 2
Объект исследования - анаграммы, палиндромы, метаграммы, абецедарии, логогрифы
Предмет исследования -
математические понятия
Гипотеза - словесные головоломки можно описать математическими понятиями
Цель работы
– выяснить, в чем особенность словесных головоломок, существует ли какая-то связь с математикой; создать сборник с занимательными лингвистическими и математическими задачами. Слайд 3Поставленные задачи:
- установить связь между математическими понятиями и словесными головоломками:
А)
анаграммами, палиндромами, метаграммами,
Б) абецедариями, логогрифами;
В) магическим словесным квадратом;
- подобрать словесные
головоломки и занимательные задачи для сборника;- попробовать составить собственные головоломки, используя полученные знания.
Методы исследования – анализ произведений русских авторов , междисциплинарное исследование, синтез.
Новизна работы в том, что исследуется пересечение математики и литературы на примере творчества русских авторов.
Практическая ценность – в создании пособия для работы на уроках русского языка, литературы и математики.
Слайд 4 ТЕХНЭ – литература, основанная на строгих формальных правилах . Греческий
термин, означающий рациональное «мастерство», «искусство». В основе технэ, искусства-техники, лежат
понятия меры и соразмерности, симметрии, гармонии и порядка. В середине ХХ века во Франции возникает группа УЛИПО (мастерская, или рукодельня потенциальной литературы), объединившая математиков и поэтов Р.Кено, Ж.Перека, Ф. Ле Лионне, Х.Кортасара, Г.Мэттьюза, И.Кальвино и других.
За основу своих литературных произведений улиписты берут такие математические формы, как: перестановки, последовательности, пределы, матрицы и др.
Р.Кено
Ж. Перек
Слайд 5В математике перестановкой из n элементов называется каждое расположение этих
элементов в определенном порядке.
Общее число возможных комбинаций вычисляется по формуле
Pn = n!
n! = n*(n-1)*(n-2)…*2*1,
где n – количество элементов текста (букв, слогов, фраз, абзацев, и т.д), в случае поэтического текста – стихов, строф, стихотворений.
Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных n элементов. В отличие от размещений в сочетаниях не имеет значения, в каком порядке указаны элементы. Два сочетания из n элементов по k отличаются друг от друга хотя бы одним элементом.
Общее число возможных сочетаний вычисляется по формуле
Глава1. Анаграммы, палиндромы, метаграммы
Слайд 6
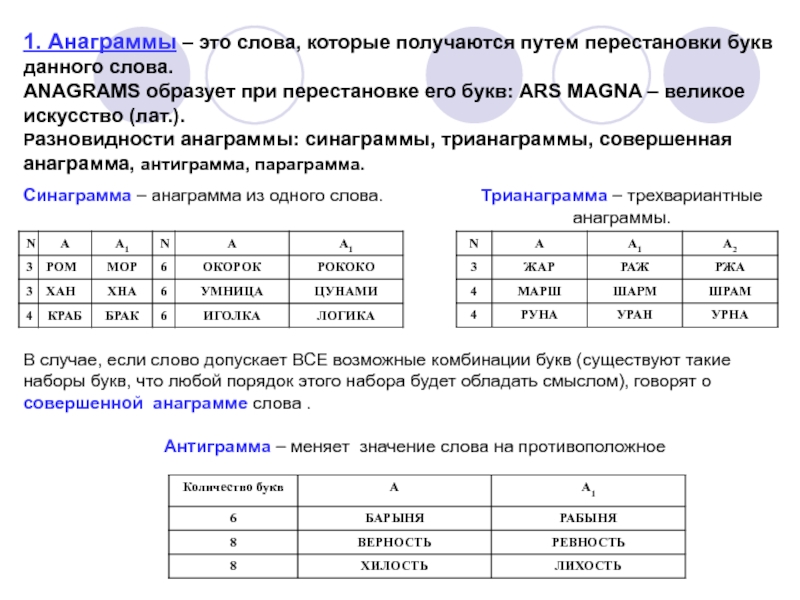
1. Анаграммы
– это слова, которые получаются путем перестановки букв данного слова.
ANAGRAMS образует при перестановке его букв: ARS MAGNA – великое искусство (лат.).Разновидности анаграммы: синаграммы, трианаграммы, совершенная анаграмма, антиграмма, параграмма.
Синаграмма – анаграмма из одного слова.
Трианаграмма – трехвариантные анаграммы.
В случае, если слово допускает ВСЕ возможные комбинации букв (существуют такие наборы букв, что любой порядок этого набора будет обладать смыслом), говорят о совершенной анаграмме слова .
Антиграмма – меняет значение слова на противоположное
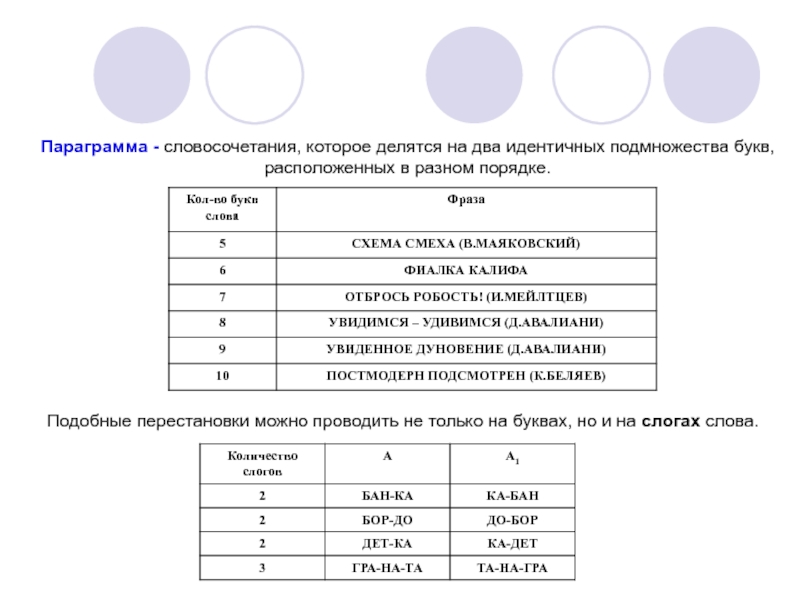
Слайд 7Параграмма - словосочетания, которое делятся на два идентичных подмножества букв,
расположенных в разном порядке.
Подобные перестановки можно проводить не только
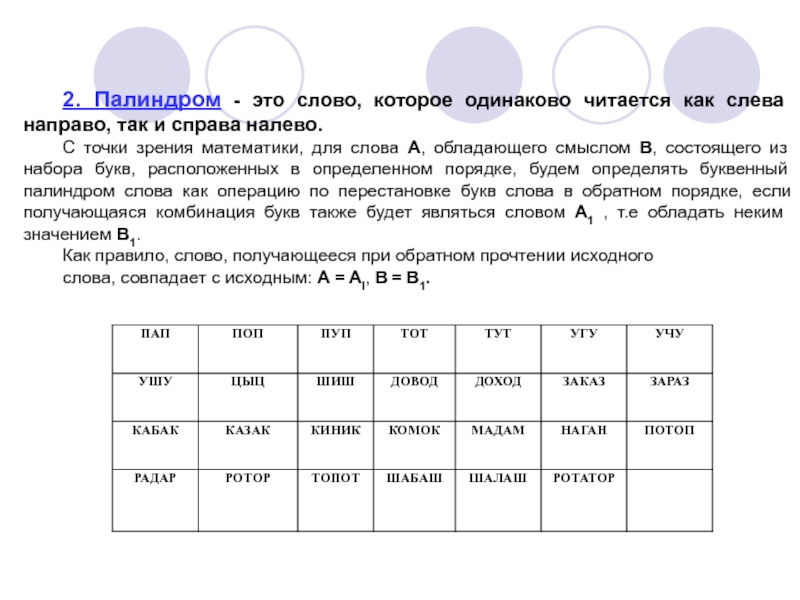
на буквах, но и на слогах слова.Слайд 82. Палиндром - это слово, которое одинаково читается как слева
направо, так и справа налево.
С точки зрения математики, для
слова A, обладающего смыслом B, состоящего из набора букв, расположенных в определенном порядке, будем определять буквенный палиндром слова как операцию по перестановке букв слова в обратном порядке, если получающаяся комбинация букв также будет являться словом A1 , т.е обладать неким значением B1. Как правило, слово, получающееся при обратном прочтении исходного
слова, совпадает с исходным: A = Al, B = B1.
Слайд 9В случае, когда при обратном прочтении получается слово, отличное от
исходного:
A = Al, B ≠ B1,
говорят о сатанинских
палиндромах, или оборотнях.Слайд 10Глава 2. Абецедарии, логогрифы,
последовательности
Абецедарий, или алфавитный текст - текст,
начальные буквы всех слов которого составляют алфавитную последовательность.
ИЮЛЬСКАЯ НОЧЬ
(Азбука от
А до Я)Алый бархат вечереет,
Горделиво дремлют ели,
Жаждет зелень, и iюль
Колыбельной лаской млеет…
Нежно отзвуки пропели…
Разостлался синий тюль.
Улетели феи – холить
Царство чары шаловливой,
Щебет ъдких эпиграмм.
Начинаетъ сны неволить,
Миро льет нетерпеливый,
Юга ясный фимиам.
В.Брюсов (1918)
Конечной числовой последовательностью называется однозначное отображение множества Аn = {1, 2, 3, …, n}, где n≥1, во множество действительных чисел. Последовательность может быть задана прямым перечислением ее членов или каким – нибудь алгебраическим выражением.
Слайд 11
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго,
равен предыдущему члену, сложенному с одним и тем же числом.
аn+1
= an + d,где d-некоторое число.an = a1 + d(n-1)
Примером арифметической прогрессии может служить логогриф.
Логогриф - загадка, в которой новые слова образуются в результате прибавления или убавления одной буквы или слога, например: «пест - перст», «мир - мираж», «Вера - Венера», «кран -экран», «спорт - порт - спор».
В математике аналогом логогрифа можно считать последовательность чисел, и, как частный случай, арифметическую прогрессию с разностью d = 1 или d= -1.
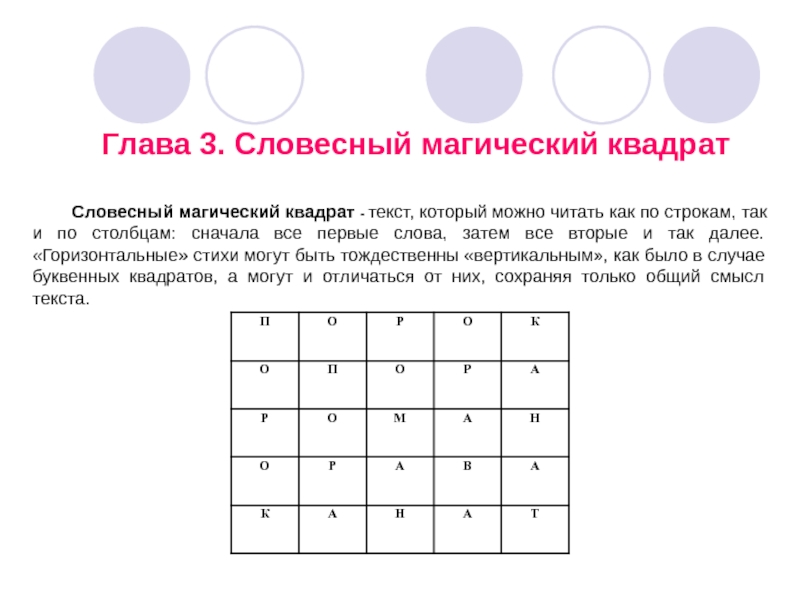
Слайд 12Глава 3. Словесный магический квадрат
Словесный магический квадрат - текст, который
можно читать как по строкам, так и по столбцам: сначала
все первые слова, затем все вторые и так далее. «Горизонтальные» стихи могут быть тождественны «вертикальным», как было в случае буквенных квадратов, а могут и отличаться от них, сохраняя только общий смысл текста.Слайд 13Словесный квадрат по своему строению очень похож на математический магических
квадрат, который по сути представляет собой матрицу.
Матрица - прямоугольная таблица
чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Матрица записывается в видеМатрицу А называют матрицей размера mxn и пишут Аmxn. Числа aij, составляющие матрицу, называют ее элементами.
Слайд 14Палиндромы и абецедарии М. Цыганковой
Палиндромы:
Шалаш латал дед, а волов тащат
казак и Анна.
Недолог тот год, а дог тот голоден.
Абецедарии:
Алеша был
веселым гулякой, деревенским ерником. Жил заботясь, искренне, крепко любя мамашу, Настеньку, оставшуюся после рождения сиротой. Трудиться умел хватко, целеустремленно, честно. Шармом щеголял этот юноша ярким.Слайд 15Список литературы
Квятковский А. Поэтический словарь. М., 1966.
Литературный энциклопедический словарь. М.,
Наука, 1987.
Авалиани Д. Лазурные кувшины. СПб., Лимбаха, 2000.
Гаспаров М.Л. Русский
стих начала XX века в комментариях. Учебное пособие. М., КД Университет, 2004.Гик Е. Заметки "Занимательное стихосложение", СПб., 2003.
Макарычев Ю.Н. Алгебра для 9 кл. сред. шк. М., Просвещение, 1990.
Александрова Г.А. Занимательный русский язык. СПб., Тригон, 1997.
Чеснокова Л.Д. На берегу лингвистики. М., Просвещение, 1996.
Макарычев Ю.Н. Элементы статистики и теории вероятностей. М., Просвещение, 2005.
Бронштейн И.Н., Справочник по математике. М., Наука, 1986.
http://www.vavilon.ru/metatext/mj54/oulipo3.html
http://www.smekalka.pp.ru/
http://www.wikipedia.org