Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
§ 4 СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
Содержание
- 1. § 4 СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- 2. СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА УГЛЫ ЭЙЛЕРАСистема координат
- 3. ТЕОРЕМА ЭЙЛЕРА - ДАЛАМБЕРАCDABB1A1ОО1 Движение твердого
- 4. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ СФЕРИЧЕСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- 5. УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ ТВЕРДОГО
- 6. ВЫЧИСЛЕНИЕ УГЛОВОГО УСКОРЕНИЯ
- 7. СКОРОСТИ ТОЧЕК ТВЕРДОГО ТЕЛА, СОВЕРШАЮЩЕГО СФЕРИЧЕСКОЕ ДВИЖЕНИЕ
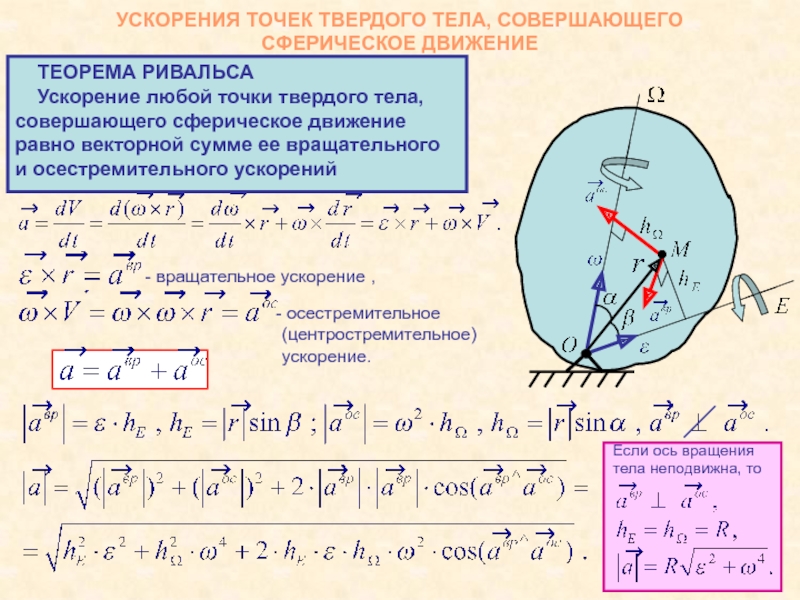
- 8. УСКОРЕНИЯ ТОЧЕК ТВЕРДОГО ТЕЛА, СОВЕРШАЮЩЕГО СФЕРИЧЕСКОЕ ДВИЖЕНИЕ
- 9. ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА Всякое перемещение
- 10. ТЕОРЕМА О СКОРОСТЯХ ТОЧЕК СВОБОДНОГО ТВЕРДОГО ТЕЛАДоказательство.
- 11. ТЕОРЕМА ОБ УСКОРЕНИЯХ ТОЧЕК СВОБОДНОГО ТВЕРДОГО ТЕЛАДоказательство.На
- 12. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1§ 4 СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
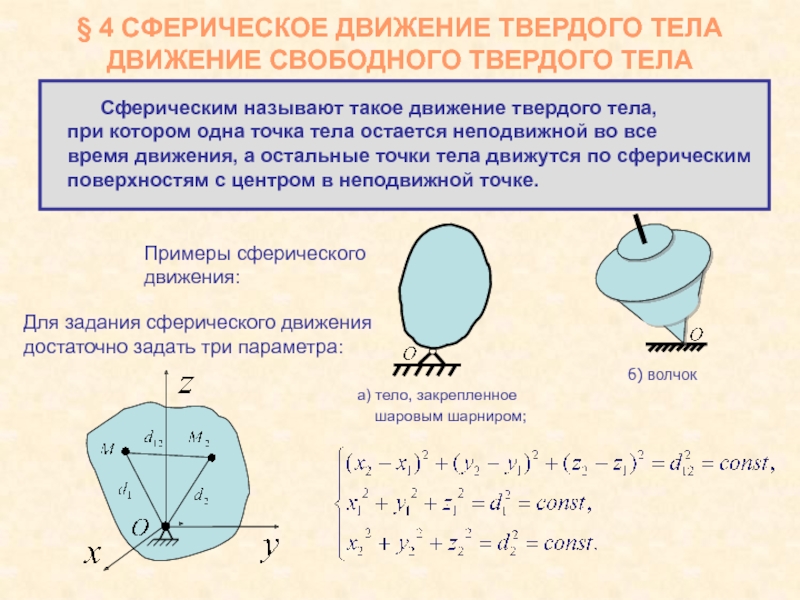
Примеры сферического
движения:
Для
задания сферического движения
Слайд 2СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
УГЛЫ ЭЙЛЕРА
Система координат Ox1y1z1 – неподвижная,
и система
координат Oxyz – подвижная,
связанная с движущимся телом, имеют
общее начало
координат – О.ОК – линия узлов
Положение подвижной системы координат относительно неподвижной
системы координат при заданных углах Эйлера можно получить с помощью
трех последовательных независимых поворотов тела: 1) на угол ψ вокруг
оси Oz1, 2) на угол θ вокруг линии узлов ОК, 3) на угол φ вокруг оси Oz.
Слайд 3ТЕОРЕМА ЭЙЛЕРА - ДАЛАМБЕРА
C
D
A
B
B1
A1
О
О1
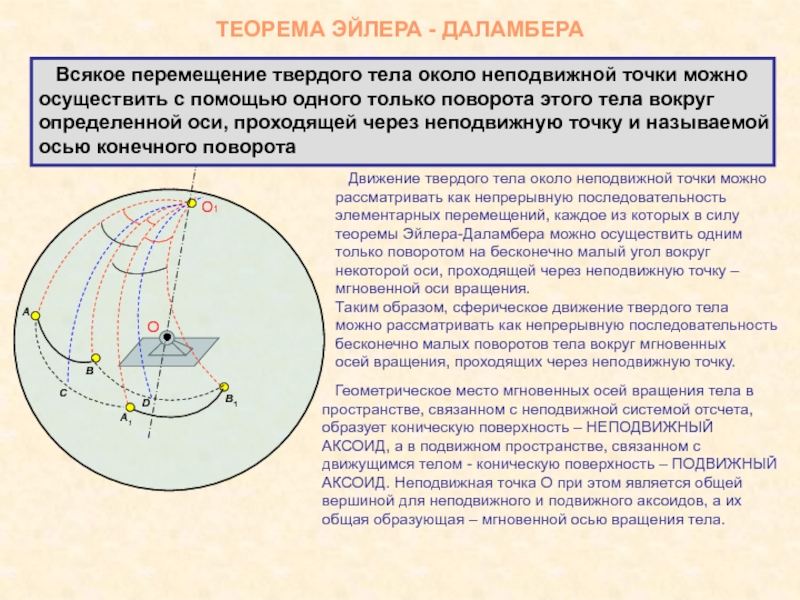
Движение твердого тела около неподвижной
точки можно
рассматривать как непрерывную последовательность
элементарных перемещений, каждое из которых в
силу теоремы Эйлера-Даламбера можно осуществить одним
только поворотом на бесконечно малый угол вокруг
некоторой оси, проходящей через неподвижную точку –
мгновенной оси вращения.
Таким образом, сферическое движение твердого тела
можно рассматривать как непрерывную последовательность
бесконечно малых поворотов тела вокруг мгновенных
осей вращения, проходящих через неподвижную точку.
Геометрическое место мгновенных осей вращения тела в
пространстве, связанном с неподвижной системой отсчета,
образует коническую поверхность – НЕПОДВИЖНЫЙ АКСОИД, а в подвижном пространстве, связанном с движущимся телом - коническую поверхность – ПОДВИЖНЫЙ АКСОИД. Неподвижная точка О при этом является общей
вершиной для неподвижного и подвижного аксоидов, а их общая образующая – мгновенной осью вращения тела.
Слайд 4ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ СФЕРИЧЕСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
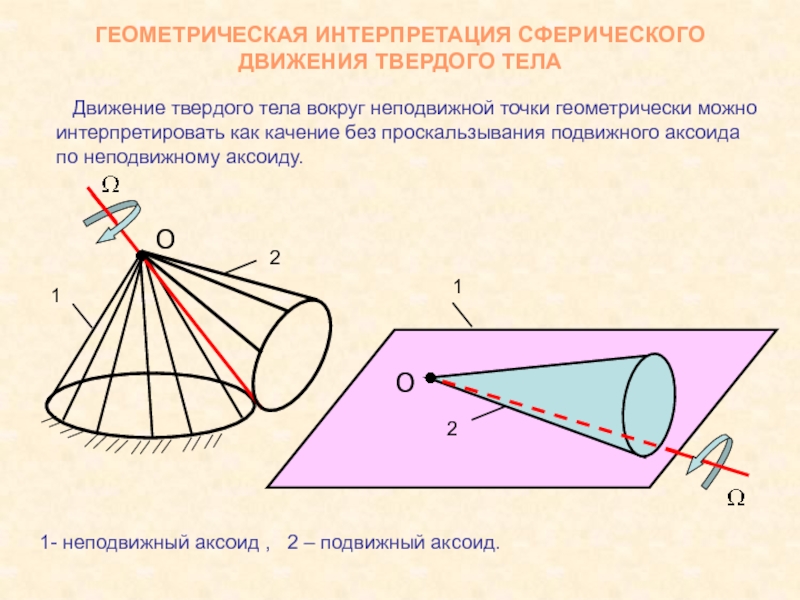
Движение твердого тела
вокруг неподвижной точки геометрически можно
интерпретировать как качение без проскальзывания подвижного
аксоидапо неподвижному аксоиду.
1- неподвижный аксоид , 2 – подвижный аксоид.
Слайд 5УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ
ТВЕРДОГО ТЕЛА ПРИ СФЕРИЧЕСКОМ ДВИЖЕНИИ
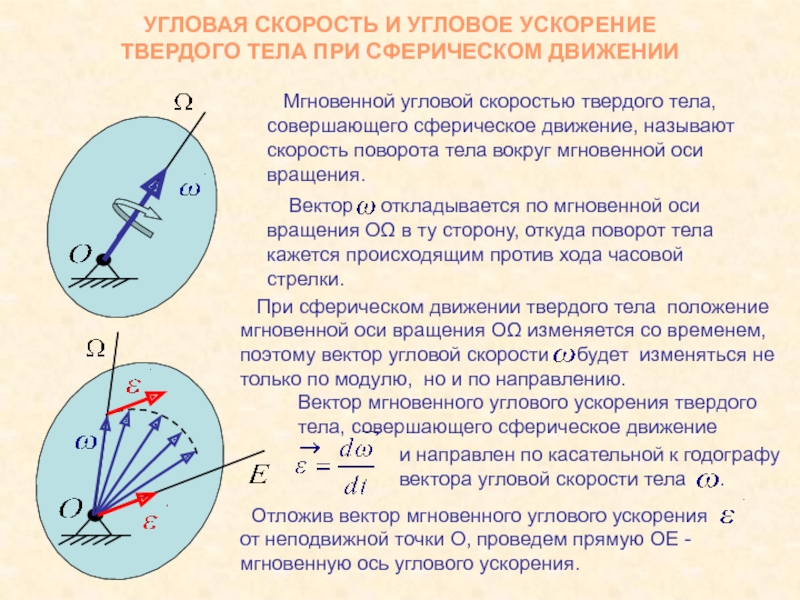
Мгновенной угловой скоростью твердого тела, совершающего сферическое движение, называют
скорость поворота тела вокруг мгновенной оси вращения.Слайд 7СКОРОСТИ ТОЧЕК ТВЕРДОГО ТЕЛА, СОВЕРШАЮЩЕГО СФЕРИЧЕСКОЕ ДВИЖЕНИЕ
Скорости точек
твердого тела, совершающего сферическое движение, в каждый
момент времени определяются как
скорости во вращении этих точек вокруг мгновенной оси вращения тела ОΩ. При этом скорости точек тела, лежащих на мгновенной оси вращения равны нулю.
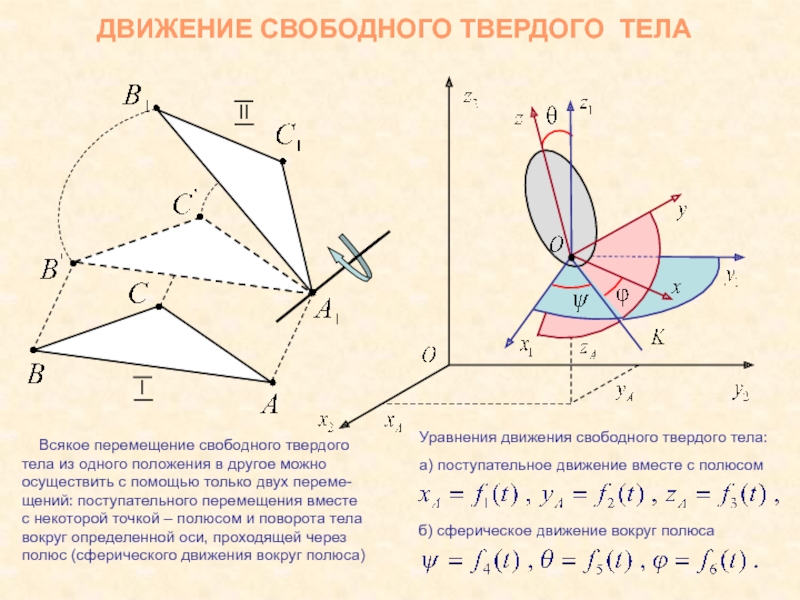
Слайд 9ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
Всякое перемещение свободного твердого
тела из
одного положения в другое можно
осуществить с помощью только двух переме-
щений:
поступательного перемещения вместес некоторой точкой – полюсом и поворота тела
вокруг определенной оси, проходящей через
полюс (сферического движения вокруг полюса)
Слайд 10ТЕОРЕМА О СКОРОСТЯХ ТОЧЕК СВОБОДНОГО ТВЕРДОГО ТЕЛА
Доказательство.
тогда
где
- скорость полюса
О ;
скорость точки М
в сферическом
движении вокруг
полюса О.
Следствия.
1) Проекции векторов
скоростей точек свободного твердого тела на прямую, соединяющую эти точкиравны (см. теорема Грасгофа);
2) Концы векторов скоростей точек свободного твердого тела, лежащих на одном, отрезке лежат на одной
прямой и делят ее в том же отношении, в каком сами точки делят отрезок;
3) Скорости точек свободного тела, лежащих на прямой, параллельной мгновенной оси вращения тела,
геометрически равны.
Слайд 11ТЕОРЕМА ОБ УСКОРЕНИЯХ ТОЧЕК СВОБОДНОГО ТВЕРДОГО ТЕЛА
Доказательство.
На основании теоремы о
скорости точки свободного твердого тела:
ускорение точки М относительно оси мгновенного
углового ускорения ОЕ; точки М относительно мгновенной оси вращения ОΩ;