1. Доказать, что перпендикуляр, проведенный из точки к прямой, меньше любой

Содержание

1. 1. Доказать, что перпендикуляр, проведенный из точки к прямой, меньше любой
2. 3.Укажите наклонные, проведенные из точки А к
3. Найти расстояние от точки А до прямой
4. 1. Объяснить, как отложить на данном луче
5. 1 ряд. Дано: Рис. 4.193. Построить:
6. DСПостроение треугольника по двум сторонам и углу
7. При любых данных отрезках AB=P1Q1, AC=P2Q2 и
8. DСПостроение треугольника по стороне и двум прилежащим
9. СПостроим луч а.Отложим отрезок АВ, равный P1Q1.Построим
10. Задача не всегда имеет решение.Во всяком треугольнике
11. Домашнее задание: § 23, 37 - повторить, § 38!!!Разобрать задачи № 283,284.
12. Скачать презентанцию

3.Укажите наклонные, проведенные из точки А к прямой BD.4. Что называется расстоянием от точки до прямой?5. Что называется расстоянием между двумя параллельными прямыми?1. Укажите отрезок, который является перпендикуляром, проведенным из точки

Главная
Разное
1. Доказать, что перпендикуляр, проведенный из точки к прямой, меньше любой

Слайды и текст этой презентации

Слайд 11. Доказать, что перпендикуляр, проведенный из точки
к прямой, меньше любой

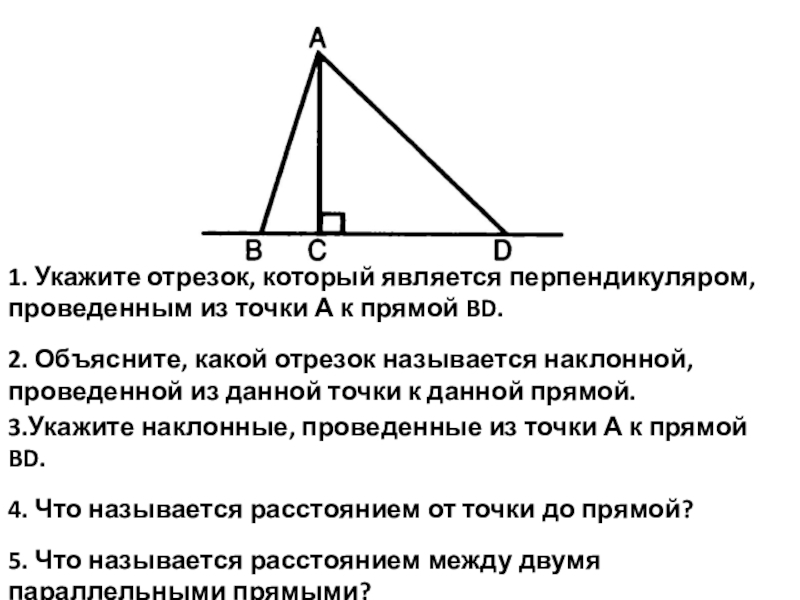
наклонной, проведенной
из этой же точки к этой прямой.

2. Доказать, что

все точки каждой из двух параллельных
прямых равноудалены от другой прямой.

3. Решить задачу № 274.

1. Доказать, что перпендикуляр, проведенный из точкик прямой, меньше любой наклонной, проведеннойиз этой же точки к этой

Слайд 23.Укажите наклонные, проведенные из точки А к прямой BD.

4. Что

называется расстоянием от точки до прямой?

5. Что называется расстоянием между

двумя параллельными прямыми?

1. Укажите отрезок, который является перпендикуляром, проведенным из точки А к прямой BD.

2. Объясните, какой отрезок называется наклонной, проведенной из данной точки к данной прямой.

3.Укажите наклонные, проведенные из точки А к прямой BD.4. Что называется расстоянием от точки до прямой?5. Что

Слайд 3Найти расстояние от точки А до прямой а.
Дано: КА

= 7 см.
Найти: расстояние от точки А до прямой

а.

Рис. 4.192.

Найти расстояние от точки А до прямой а. Дано: КА = 7 см. Найти: расстояние от точки

Слайд 41. Объяснить, как отложить на данном луче от его начала

отрезок, равный данному.

2. Объяснить, как отложить от данного луча угол,

равный данному.

3. Объяснить, как построить биссектрису данного угла.

4. Объяснить, как построить прямую, проходящую через данную точку, лежащую на данной прямой, и перпендикулярную к этой прямой.

5. Объяснить, как построить середину данного отрезка.

Построение треугольника по трём элементам.

1. Объяснить, как отложить на данном луче от его начала отрезок, равный данному.2. Объяснить, как отложить от

Слайд 51 ряд. Дано: Рис. 4.193.
Построить: АВС такой,

что АВ = PQ, A= М, В

= N, с помощью циркуля и линейки без делений.

2 ряд. Дано: Рис. 4.194.
Построить: АВС такой, что АВ = MN, AC= RS, A= Q, с помощью циркуля и линейки без делений.
3 ряд. Дано: Рис. 4.195.
Построить: АВС такой, что АВ = MN, ВС = PQ, AC= RS, с помощью циркуля и линейки без делений.

1 ряд. Дано: Рис. 4.193. Построить: АВС такой, что АВ = PQ, A=

Слайд 6D
С
Построение треугольника по двум сторонам и углу между ними.

hk
h
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим

угол, равный данному.
Отложим отрезок АС, равный P2Q2.

Δ АВС искомый.

Дано:

Отрезки Р1Q1 и Р2Q2 ,

Док-во: По построению AB=P1Q1, AC=P2Q2, A= hk.

Построить .

Построение.

Слайд 7При любых данных отрезках AB=P1Q1, AC=P2Q2 и данном неразвернутом

hk искомый треугольник построить можно.
Так как прямую а и

точку А на ней можно выбрать произвольно, то существует бесконечно много треугольников, удовлетворяющих условиям задачи. Все эти треугольники равны друг другу (по первому признаку равенства треугольников), поэтому принято говорить, что данная задача имеет единственное решение.