Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 1 Учебный военный центр Цикл боевого применения самоходной
Содержание
- 1. 1 1 Учебный военный центр Цикл боевого применения самоходной
- 2. ТЕМА № 5. Топогеодезическое обеспечение боевых действий артиллерии. Основные элементы геодезических вычислений.
- 3. Учебные и воспитательные целиВ результате изучения темы
- 4. Определить полярные координаты между:1-й вариант:Сараем (5310) и
- 5. 1. Цель и задачи топогеодезического обеспечения боевых действий артиллерии. Основные элементы геодезических вычислений.
- 6. ТурПростая пирамидаПростой сигналС л о ж
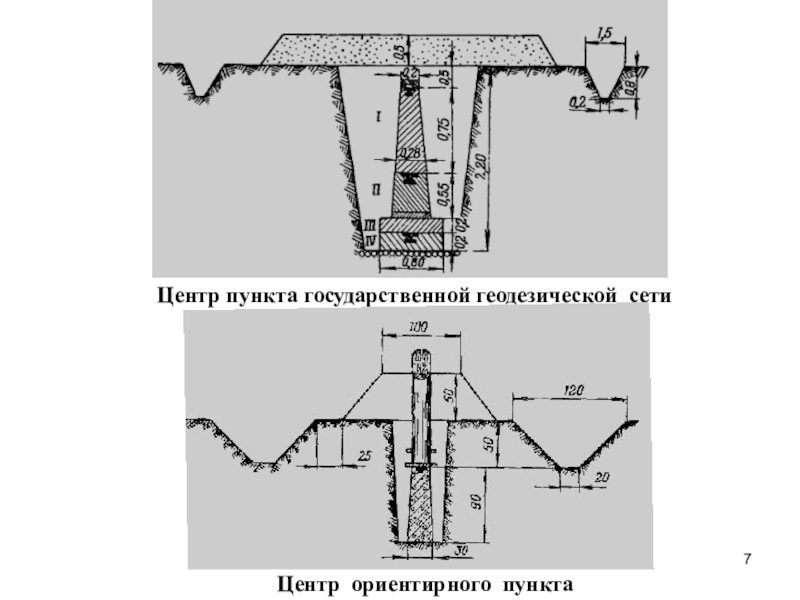
- 7. Центр пункта государственной геодезической сетиЦентр ориентирного пункта
- 8. ТрехграннаяпирамидаСтандартный центр пункта специальнойгеодезической сетиЦентр ориентирного пунктаСпециальная геодезическая сеть (СГС).
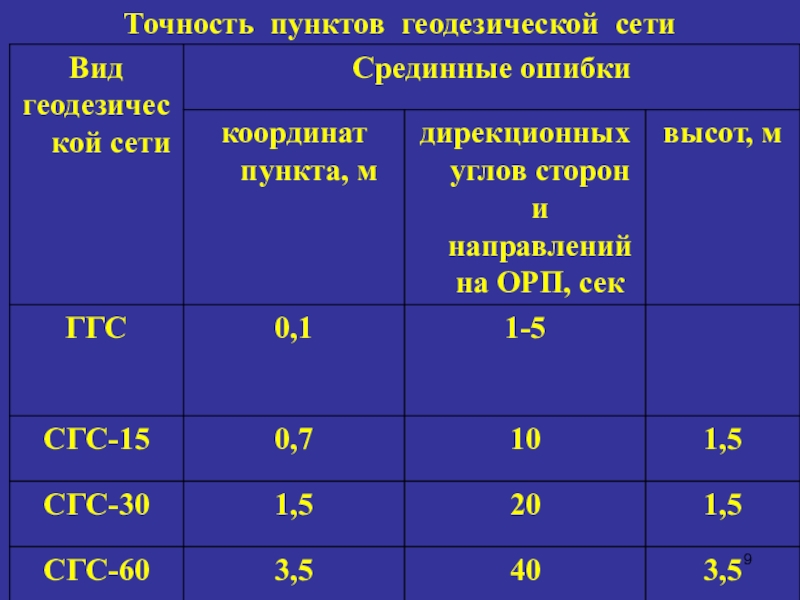
- 9. Точность пунктов геодезической сети
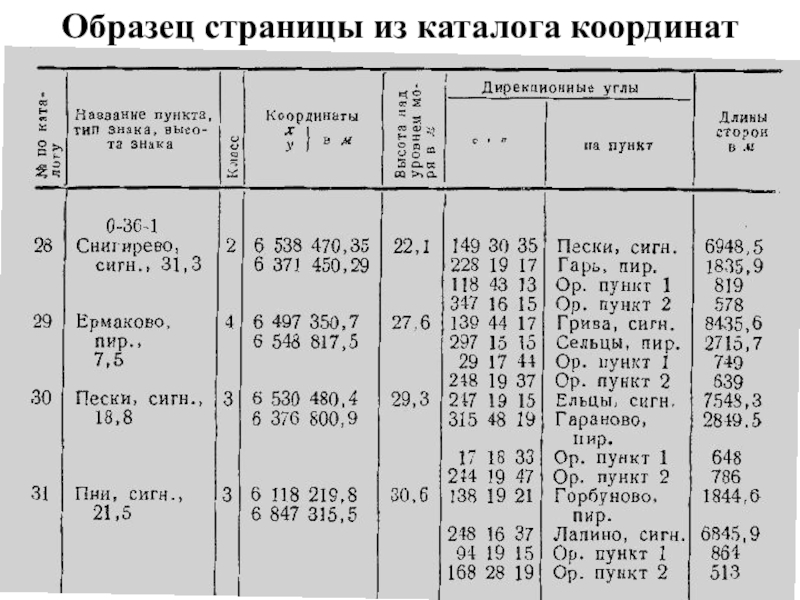
- 10. Образец страницы из каталога координат
- 11. aПереход от дирекционного угла одного направления
- 12. aПереход от дирекционного угла одного направления
- 13. Определение величины горизонтального угла по дирекционным углам направлений, составляющих этот угол. α1β = α2 – α1βα2
- 14. Определение величины горизонтального угла по дирекционным углам
- 15. 2. Преобразование полярных координат в прямоугольные аналитическим методом. Решение ПГЗ.
- 16. АВXYс∆У∆ХХАУАХВУВДαСущность прямой геодезической задачи.∆Х = Д х
- 17. aaaВВВВАЗнаки приращений координатУХ1 α = 0 –
- 18. сos 53-37 = + 0,76853-00 0-30 0-40ОПРЕДЕЛЕНИЕ
- 19. Пример №1: Определить прямоугольные координаты цели, если
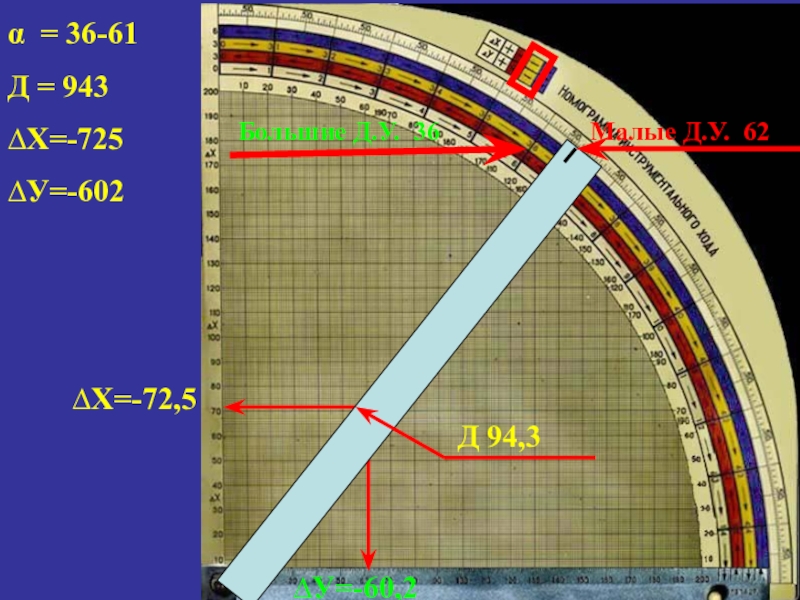
- 20. α = 36-61Д = 943∆Х=-725∆У=-602Д 94,3∆Х=-72,5∆У=-60,2Большие Д.У. 36Малые Д.У. 62
- 21. Определить координаты цели, еслиКНП Х= 53870
- 22. 3. Преобразование прямоугольных координат в полярные аналитическим методом. Решение ОГЗ.
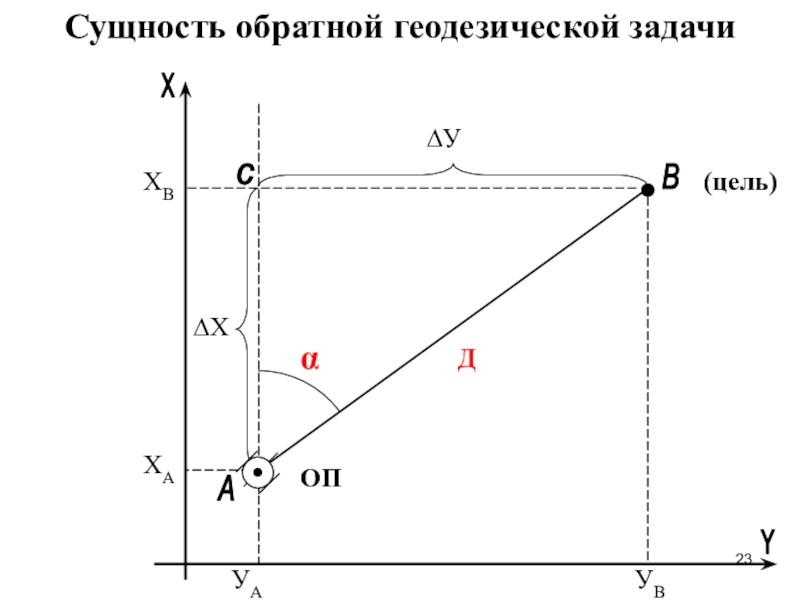
- 23. АВXYсХАХВУАУВ∆Х∆Уα ДОП (цель)Сущность обратной геодезической задачи
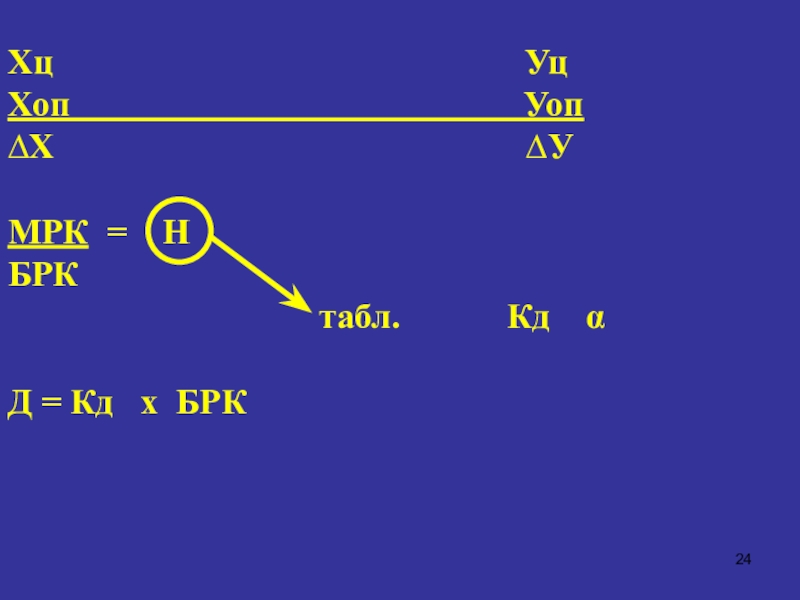
- 24. Хц
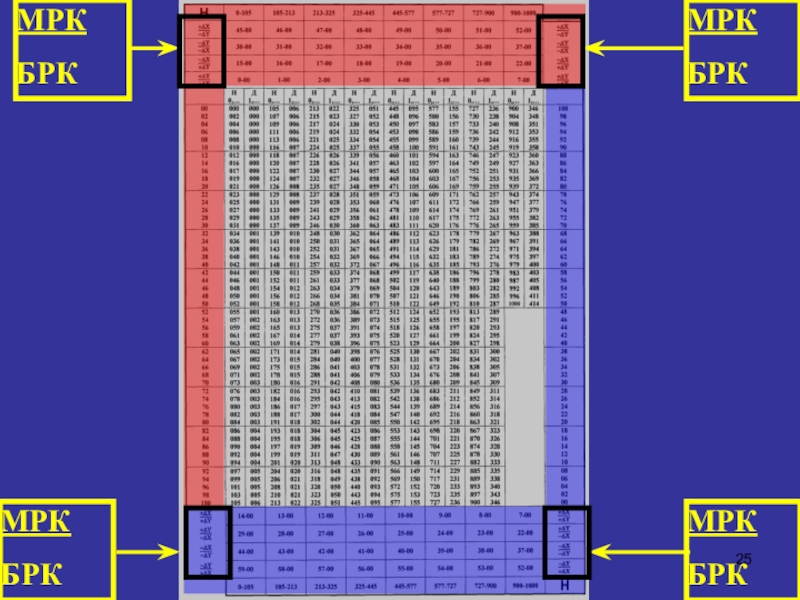
- 25. МРКБРКМРКБРКМРКБРКМРКБРК
- 26. Хц =57460 Уц =24560Хоп =53180 Уоп=23596∆Х=
- 27. Определить полярные координаты цели с ОП если:
- 28. Хц
- 29. 4. Определение дальности по короткой базе. Решение треугольника.
- 30. βγ15-00КТД= ?Определение дальности по короткой базе.γ= 30-00
- 31. БазаБазаДальностьДальностьУгол засечкиУгол засечки
- 32. Определить расстояние, если, β=12-72, Б=76м.Решение:γ=15-00 – 12-72 = 2-282-208Для Б=10м Д=41мДля Б=76м Д=41 х 7,6= 312м
- 33. Пример:Определить Д если Б=56 β= 13-43Б=72
- 34. САВАВСДпрДлевРешение треугольникаДлев = (Б : sin С)
- 35. Пример:Определить дальности если Б=78м А=11-28
- 36. eАВhАhВ∆hДГДИУровненная поверхностьhВ = hА + ∆h∆h =
- 37. e Приведение наклонных расстояний к горизонту.ДИДГГ о
- 38. Задание на самостоятельную работу: Изучить:Руководство по боевой
- 39. Скачать презентанцию
Слайды и текст этой презентации
Слайд 11
Учебный военный центр
Цикл боевого применения самоходной артиллерии
Тольяттинский государственный университет
Слайд 2ТЕМА № 5. Топогеодезическое обеспечение боевых действий артиллерии. Основные элементы
геодезических вычислений.
Слайд 3Учебные и воспитательные цели
В результате изучения темы студенты должны
Знать:
цель
и задачи топогеодезического обеспечения боевых действий артиллерии;
основные элементы геодезических
вычислений;порядок решения ПГЗ;
порядок решения ОГЗ;
порядок определения дальности по короткой базе, решения треугольника.
Уметь:
решать ПГЗ аналитическим методом;
решать ОГЗ аналитическим методом ;
определять дальность по короткой базе, решать треугольник аналитическим методом.
Слайд 4Определить полярные координаты между:
1-й вариант:
Сараем (5310) и школой (5312)
Сараем (5310)
и трубой (5213)
Сараем (5310) и отм. 165,4 (5709)
2-й вариант:
Отм. 159,7
(6810) и ж.д. станцией (6813)Отм. 159,7 (6810) и церковью (6713)
Отм. 159,7 (6810) и мельницой (7109)
3-й вариант:
Бродом (6414) и колодцем (6015)
Бродом (6414) и отм. 254,0 (6612)
Бродом (6414) и мельницой (6817)
Слайд 51. Цель и задачи топогеодезического обеспечения боевых действий артиллерии. Основные
элементы геодезических вычислений.
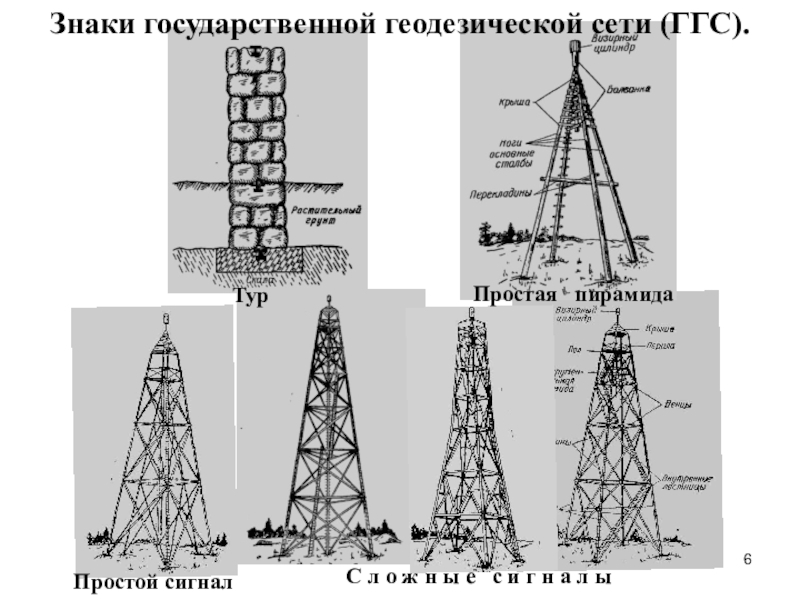
Слайд 6Тур
Простая пирамида
Простой сигнал
С л о ж н ы е
с и г н а л ы
Знаки государственной геодезической
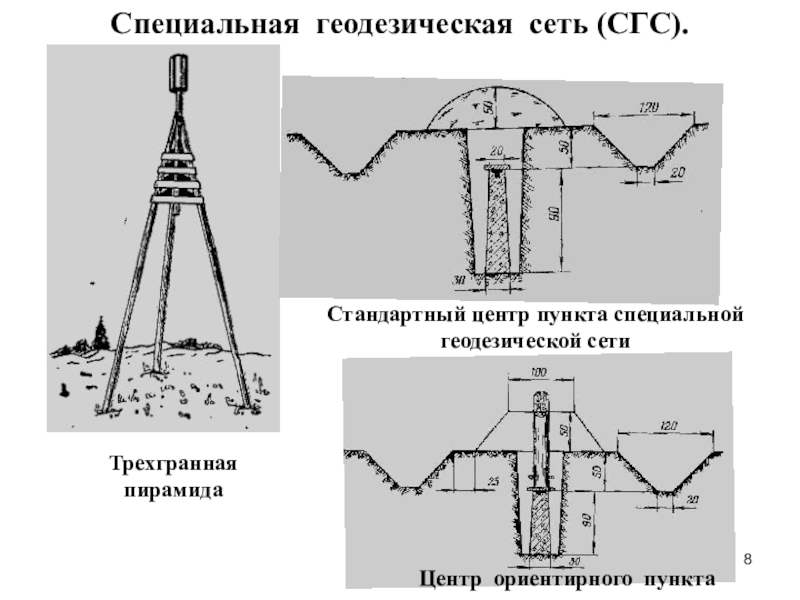
сети (ГГС).Слайд 8Трехгранная
пирамида
Стандартный центр пункта специальной
геодезической сети
Центр ориентирного пункта
Специальная геодезическая сеть (СГС).
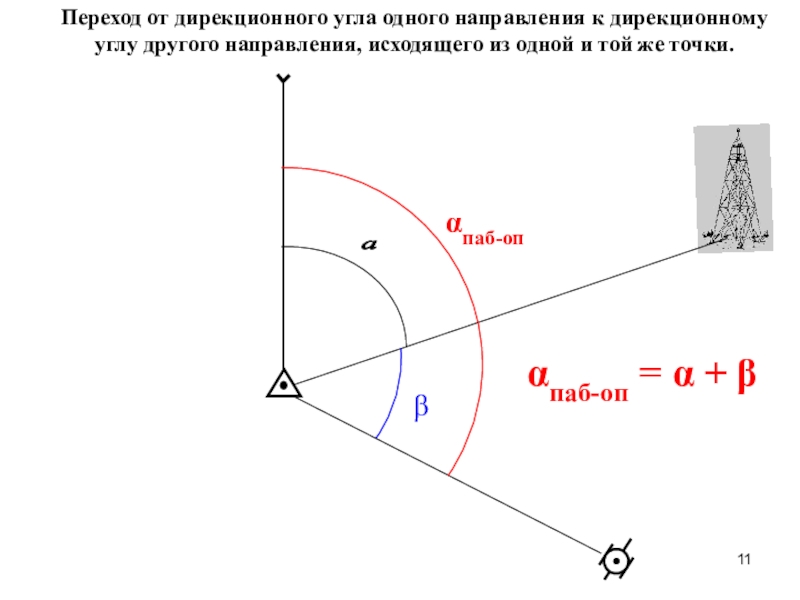
Слайд 11 a
Переход от дирекционного угла одного направления к дирекционному углу
другого направления, исходящего из одной и той же точки.
αпаб-оп
αпаб-оп =
α + ββ
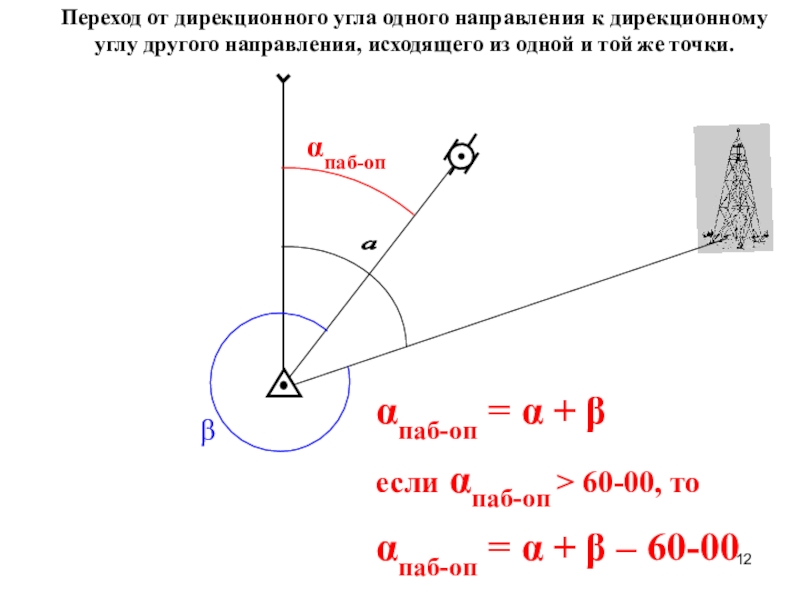
Слайд 12 a
Переход от дирекционного угла одного направления к дирекционному углу
другого направления, исходящего из одной и той же точки.
αпаб-оп
αпаб-оп =
α + βесли αпаб-оп > 60-00, то
αпаб-оп = α + β – 60-00
β
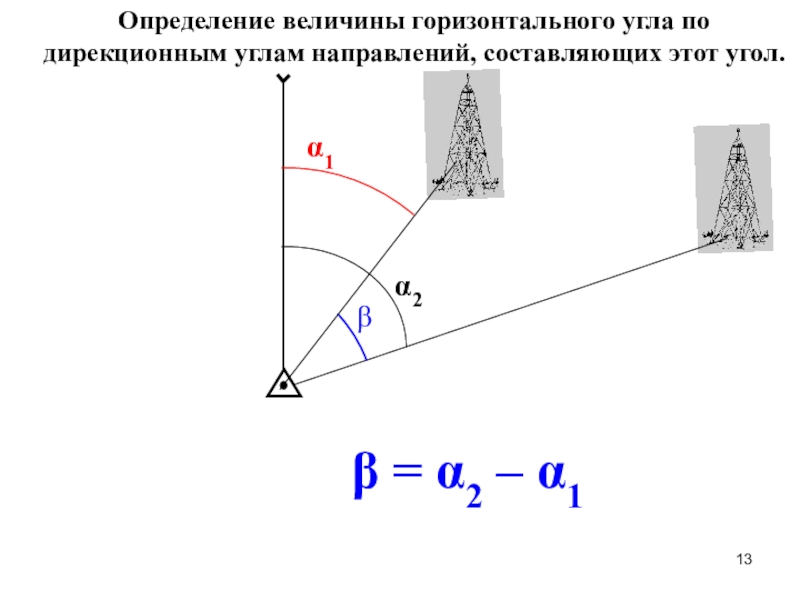
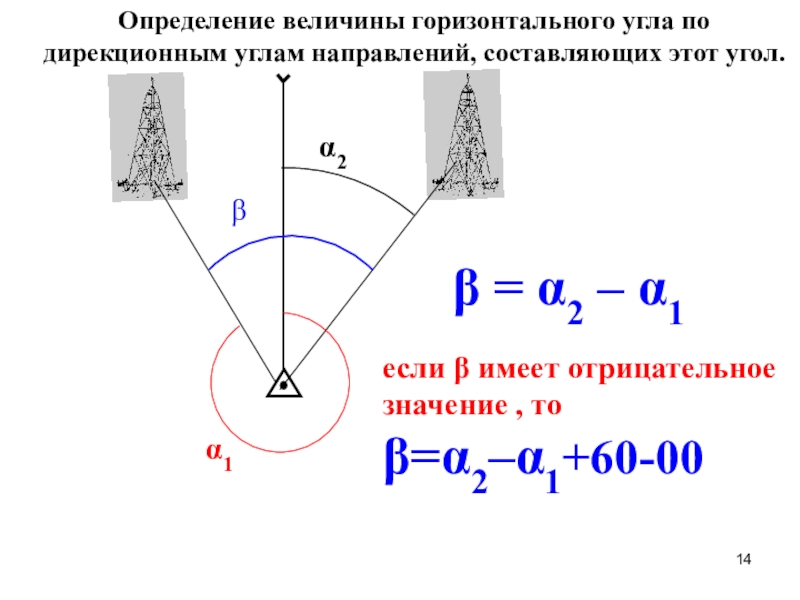
Слайд 13Определение величины горизонтального угла по дирекционным углам направлений, составляющих этот
угол.
α1
β = α2 – α1
β
α2
Слайд 14Определение величины горизонтального угла по дирекционным углам направлений, составляющих этот
угол.
α1
β = α2 – α1
β
α2
если β имеет отрицательное значение
, то β=α2–α1+60-00Слайд 16А
В
X
Y
с
∆У
∆Х
ХА
УА
ХВ
УВ
Д
α
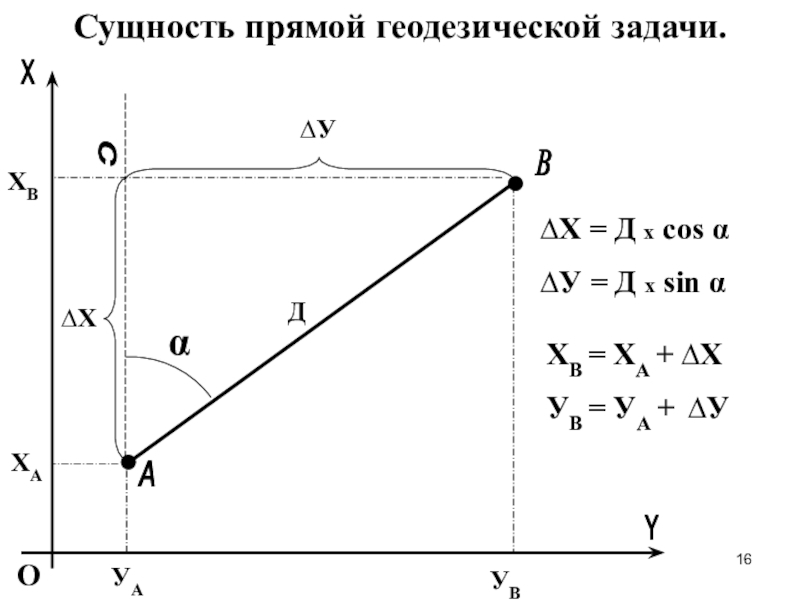
Сущность прямой геодезической задачи.
∆Х = Д х cos α
∆У =
Д х sin α
ХВ = ХА + ∆Х
УВ = УА
+ ∆У О
Слайд 17a
a
a
В
В
В
В
А
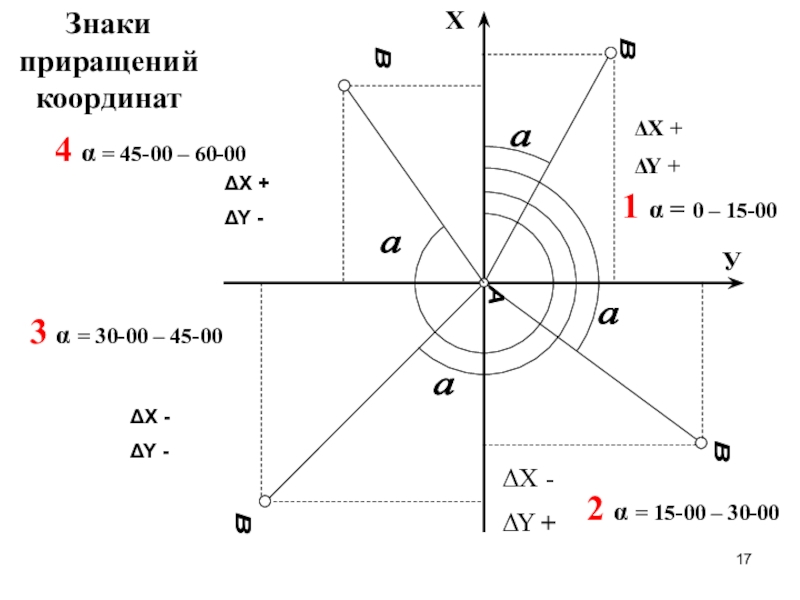
Знаки приращений координат
У
Х
1 α = 0 – 15-00
+
+
2 α = 15-00 – 30-00
-
+
3 α = 30-00 – 45-00
-
-
a
4 α = 45-00 – 60-00
+
-
Слайд 18сos 53-37 = + 0,768
53-00
0-30
0-40
ОПРЕДЕЛЕНИЕ sin и cos
УГЛОВ С ИСПОЛЬЗОВАНИЕМ ТАБЛИЦ
sin 53-37 = - 0,632
53-00
0-30
0-40
Слайд 19Пример №1:
Определить прямоугольные координаты цели, если с наблюдательного пункта
Хнп=54280 Унп=18320 определены полярные координаты α = 13-24, Д=3427.
Решение:
а) с
использованием инженерного микрокалькулятора∆Х = Д х cos α = 13,24 х 6 = (79,44) cos (+0,183265087) х 3427 = +628
∆У = Д х sin α = 13,24 х 6 = (79,44) sin (+0,983063531) х 3427 = +3368
б) с использованием таблиц синусов и косинусов
∆Х = Д х cos α = 3427 х (+0,183) = +627
∆У = Д х sin α = 3427 х (+0,983) = +3369
Хц = Хнп + ∆Х = 54280 + (+628) = 54908
Уц = Унп + ∆У = 18320 + (+3368) = 21688
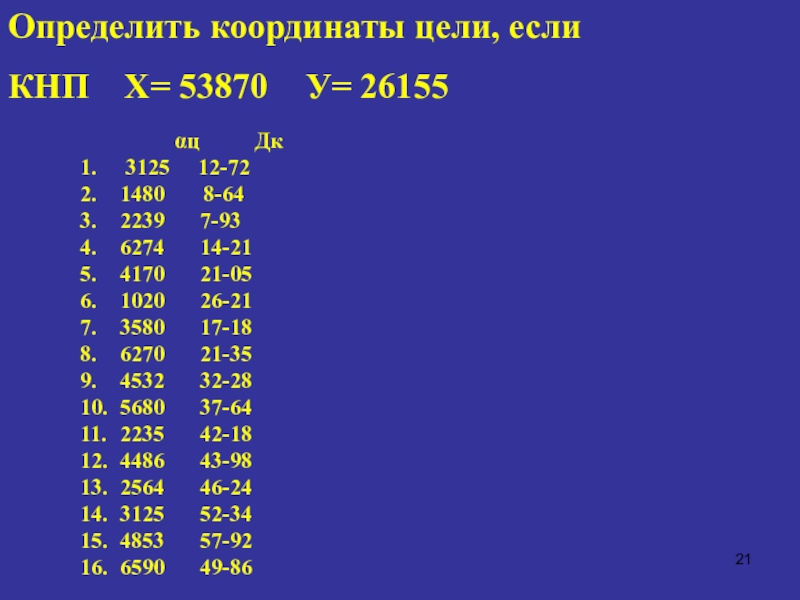
Слайд 21Определить координаты цели, если
КНП Х= 53870 У= 26155
αц
Дк1. 3125 12-72
2. 1480 8-64
3. 2239 7-93
4. 6274 14-21
5. 4170 21-05
6. 1020 26-21
7. 3580 17-18
8. 6270 21-35
9. 4532 32-28
10. 5680 37-64
11. 2235 42-18
12. 4486 43-98
13. 2564 46-24
14. 3125 52-34
15. 4853 57-92
16. 6590 49-86
Слайд 26Хц =57460 Уц =24560
Хоп =53180 Уоп=23596
∆Х= +4280 ∆У=+964
Н=
МРК : БРК = + ∆У:(+∆Х) = 964 : 4280=
0,2252336≈ 0,225α= 2-11
Кд= 1,025
Д= БРК х Кд
=1,025х4280= 4387
Определить полярные координаты цели с ОП если: Хоп =56496 Уоп=20280 Хц =57460 Уц =24560
Ответ: α = 2-11 Д = 4387
Слайд 27Определить полярные координаты цели с ОП если: Хоп =67250 Уоп=31540
Хц =64147 Уц =24260
Хц =64147 Уц =24260
Хоп =67250
Уоп=31540∆Х= - 3103 ∆У= -7280
Н= МРК : БРК = - ∆Х : -∆У = 3103 : 7280 = 0,4262362≈ 0,426
α= 41-15
Кд= 1,025
Д= БРК х Кд =1,087х7280= 7913
Ответ: α = 41-15 Д = 7913
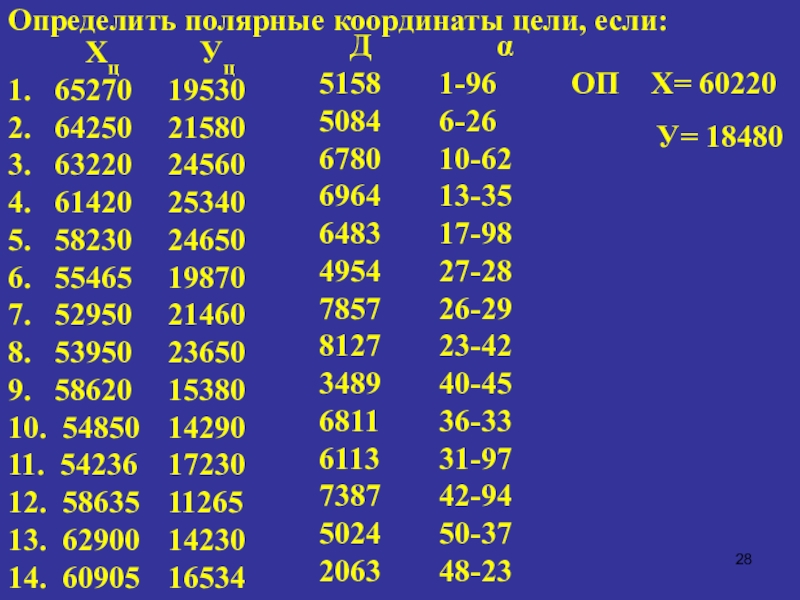
Слайд 28 Хц
Уц
1. 65270 19530
2. 64250 21580
3. 63220 24560
4. 61420 25340
5.
58230 246506. 55465 19870
7. 52950 21460
8. 53950 23650
9. 58620 15380
10. 54850 14290
11. 54236 17230
12. 58635 11265
13. 62900 14230
14. 60905 16534
Д α
5158 1-96
5084 6-26
6780 10-62
6964 13-35
6483 17-98
4954 27-28
7857 26-29
8127 23-42
3489 40-45
6811 36-33
6113 31-97
7387 42-94
5024 50-37
2063 48-23
Определить полярные координаты цели, если:
ОП Х= 60220
У= 18480
Слайд 30β
γ
15-00
КТ
Д= ?
Определение дальности по короткой базе.
γ= 30-00 – 15-00 –
β
γ= 15-00 – β
Д определяют:
по НИХ
по таблице
по формуле: Д =
Б : tg γИсходные данные: Б и γ
Б
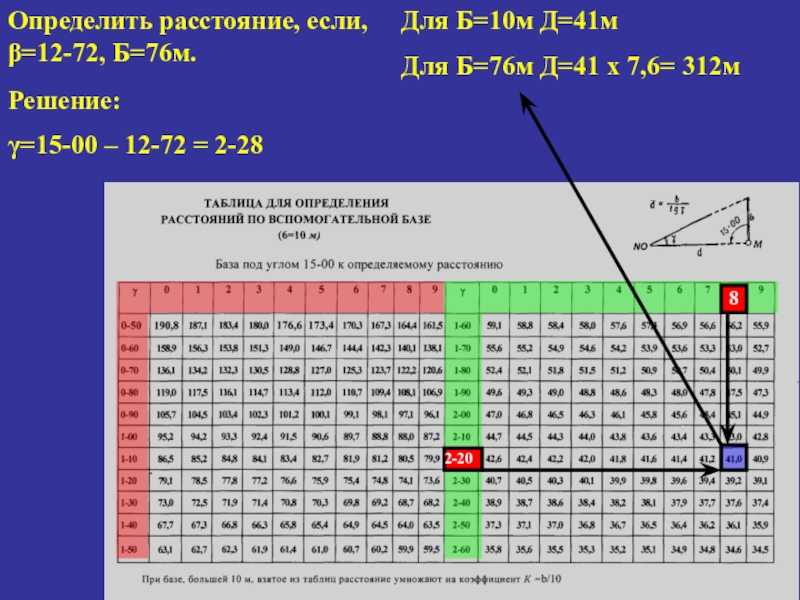
Слайд 32Определить расстояние, если, β=12-72, Б=76м.
Решение:
γ=15-00 – 12-72 = 2-28
2-20
8
Для Б=10м
Д=41м
Для Б=76м Д=41 х 7,6= 312м
Слайд 33Пример:
Определить Д если
Б=56 β= 13-43
Б=72 β= 12-38
Б=36 β= 13-18
γ=1-57 Д=337м
γ=2-62 Д=256м
γ=1-82 Д=186м
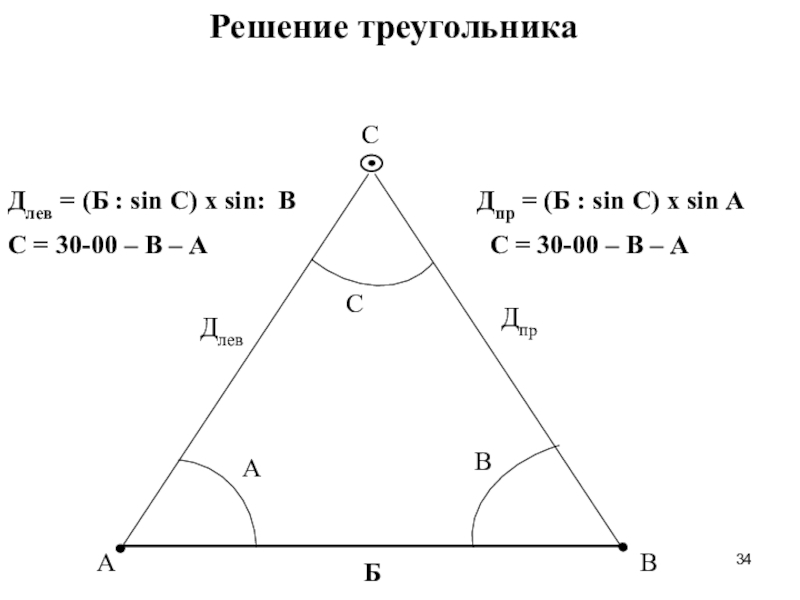
Слайд 34С
А
В
А
В
С
Дпр
Длев
Решение треугольника
Длев = (Б : sin С) х sin: В
Дпр = (Б : sin С)
х sin АБ
C = 30-00 – В – А
C = 30-00 – В – А
Слайд 35Пример:
Определить дальности если Б=78м А=11-28 В=16-34
C = 30-00
– В – А = 30-00 – 11-28 - 16-34
= 2-38Длев = (Б : sin С) х sin В= (78 : 0,247) х 0,99 = 312м
Дпр = (Б : sin С) х sin А = (78 : 0,247) х 0,925 = 292м
Слайд 36e
А
В
hА
hВ
∆h
ДГ
ДИ
Уровненная поверхность
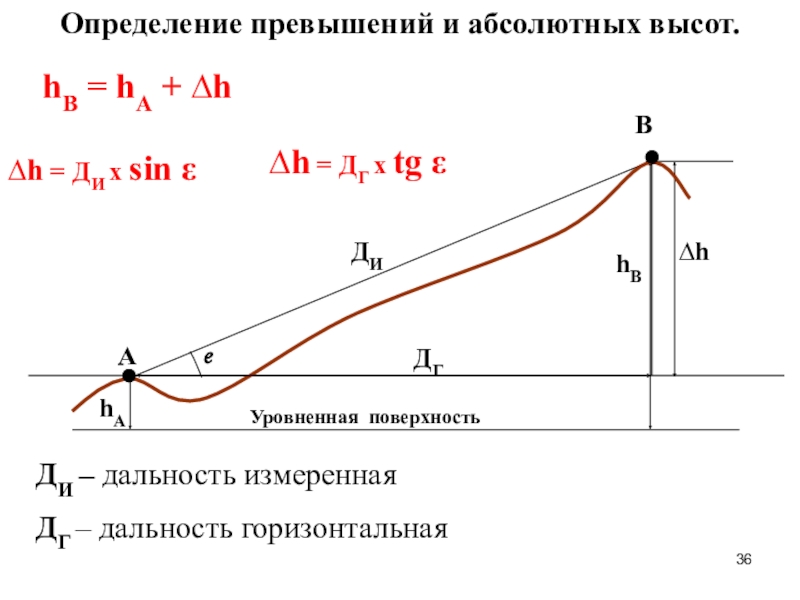
hВ = hА + ∆h
∆h = ДИ х sin
ε
∆h = ДГ х tg ε
Определение превышений и абсолютных высот.
ДИ – дальность измеренная
ДГ – дальность горизонтальная
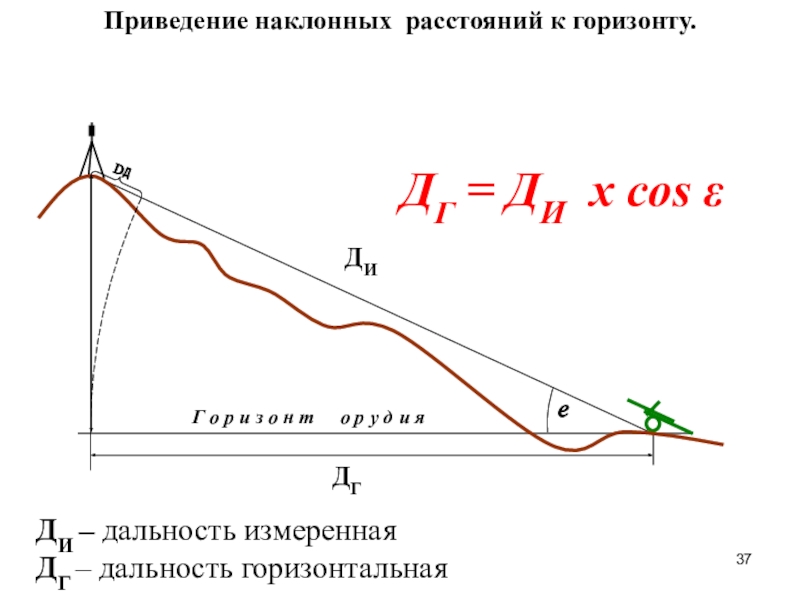
Слайд 37e
Приведение наклонных расстояний к горизонту.
ДИ
ДГ
Г о р и з
о н т о р у д и
яДГ = ДИ х cos
ДИ – дальность измеренная
ДГ – дальность горизонтальная
Слайд 38Задание на самостоятельную работу:
Изучить:
Руководство по боевой работе топогеодезических подразделений
РВ и А, групп самопривязки и расчетов машин, оснащенных автономной
навигационной аппаратурой. Воениздат 2008 г. Глава 1,2.К занятию повторить:
цель и задачи топогеодезического обеспечения боевых действий артиллерии;
основные элементы геодезических вычислений;
порядок решения ПГЗ;
порядок решения ОГЗ;
порядок определения дальности по короткой базе, решение треугольника.