передаточная функция содержит полиномы небольшой степени (не выше второй) комплексной
переменной p в числителе или в знаменателе.Классификация типовых динамических звеньев
Минимально фазовые звенья –это звенья, передаточные функции которых могут содержать в своей структуре как нули, так и полюсы, причем полюсы могут иметь отрицательные вещественные части, быть нулевыми или чисто мнимыми.
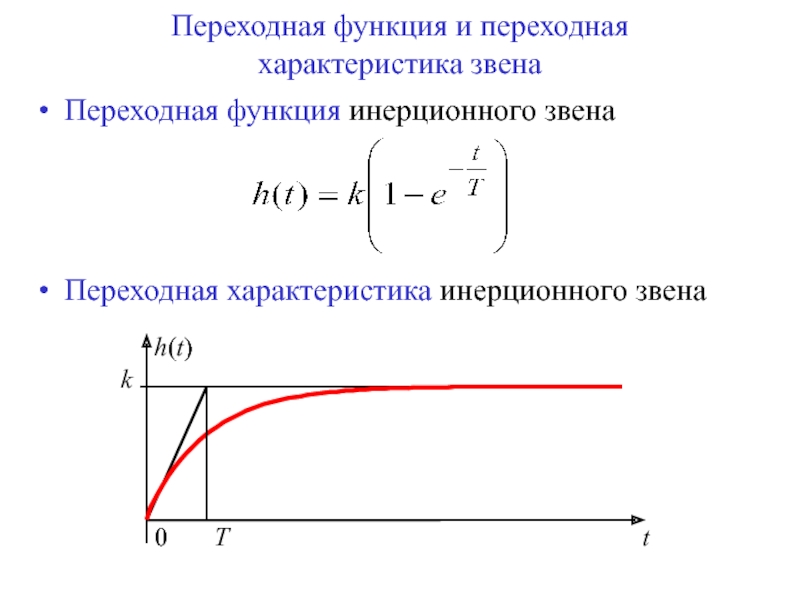
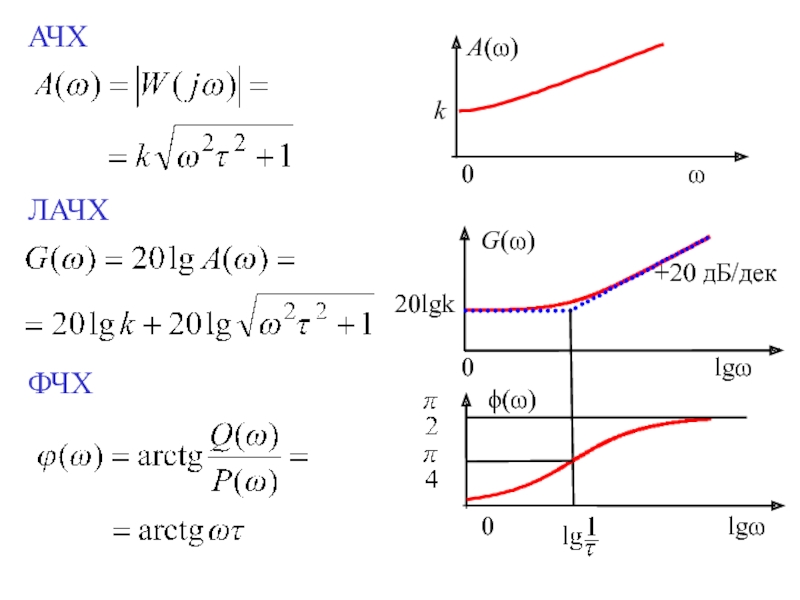
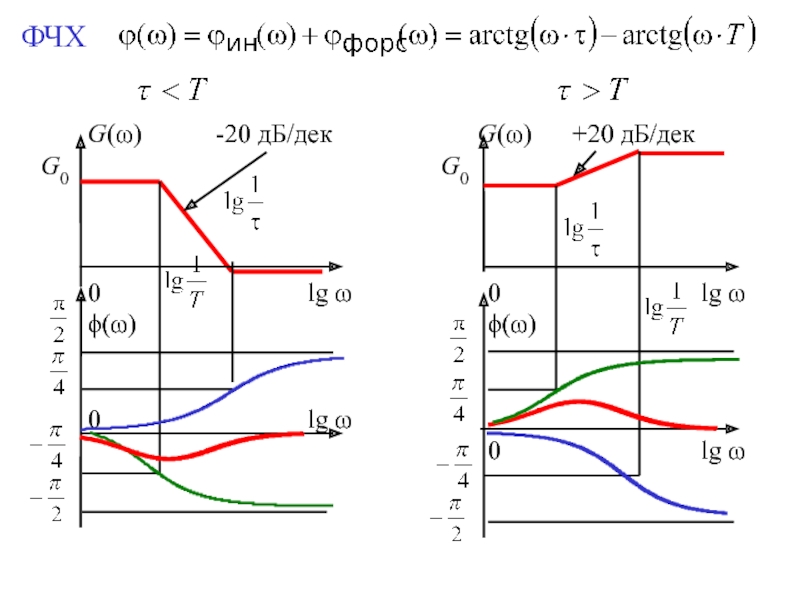
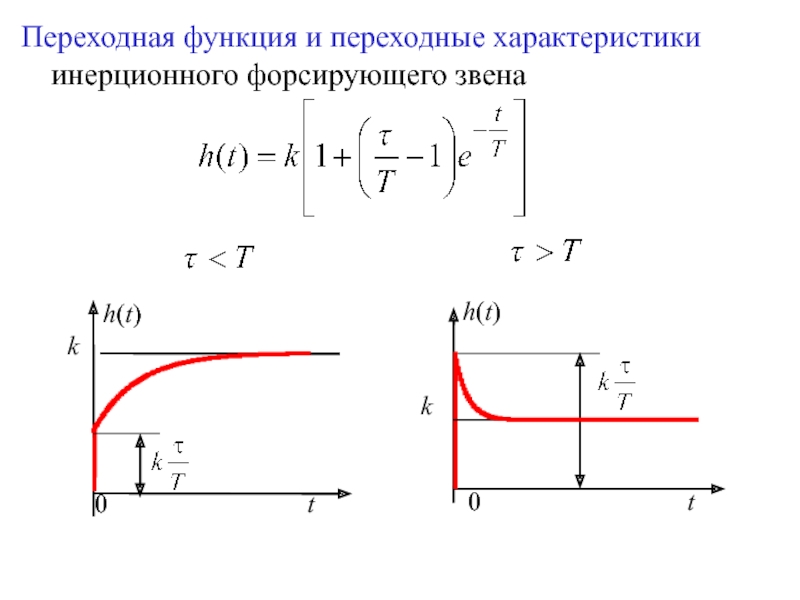
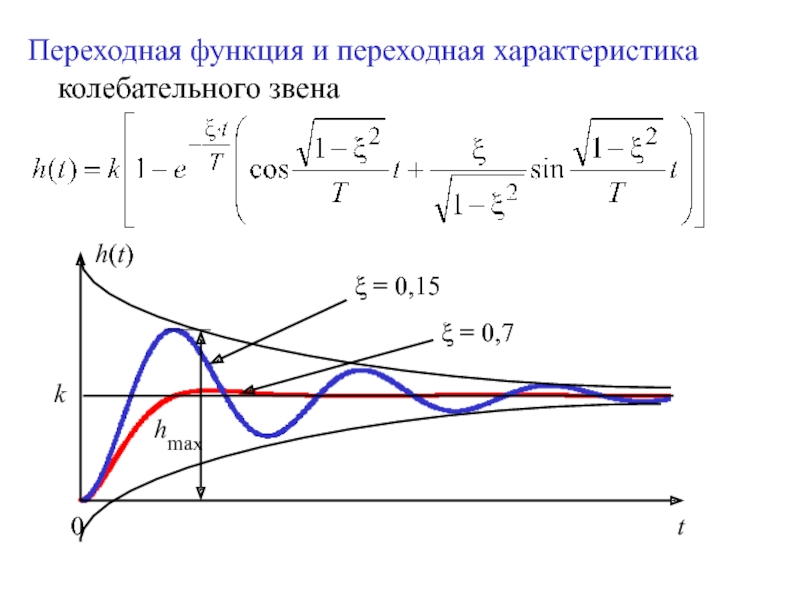
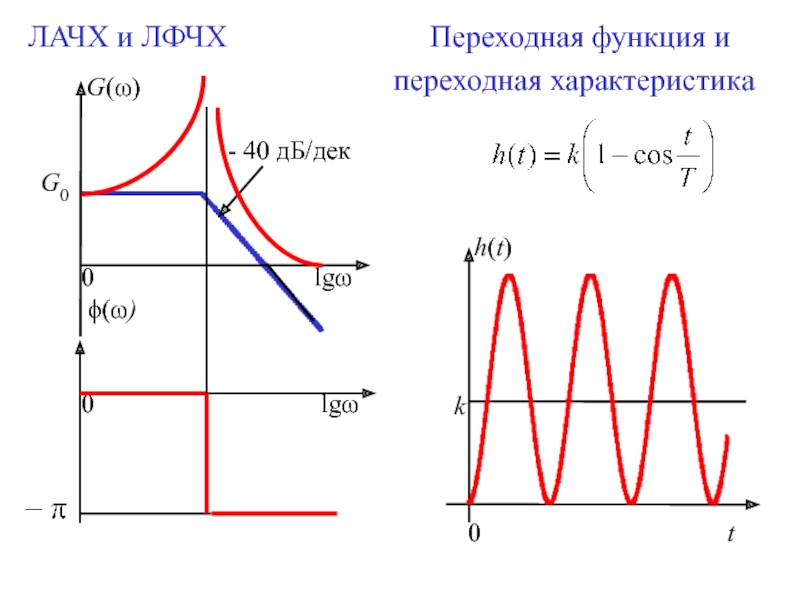
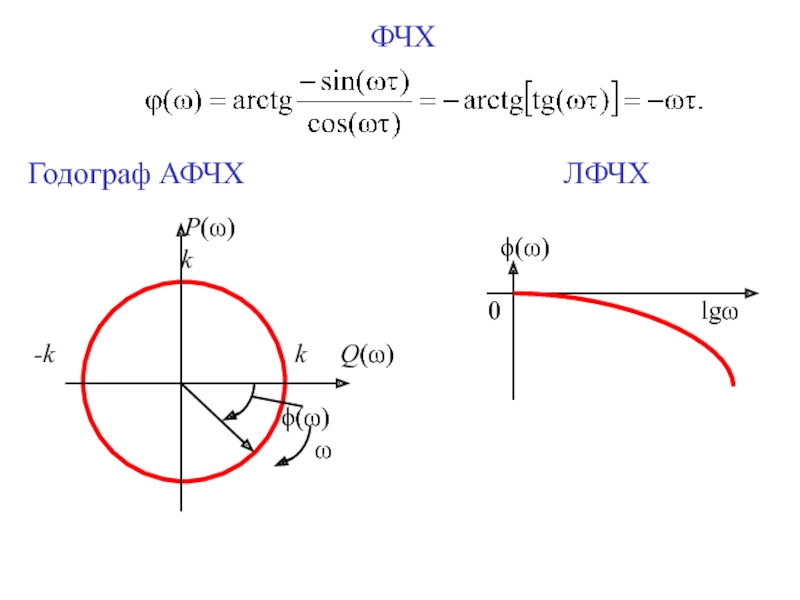
Для минимально фазовых звеньев









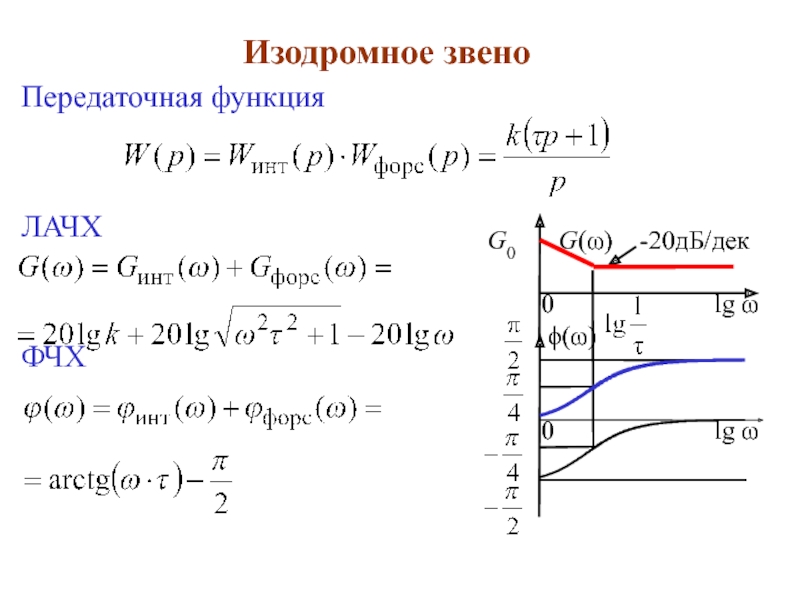
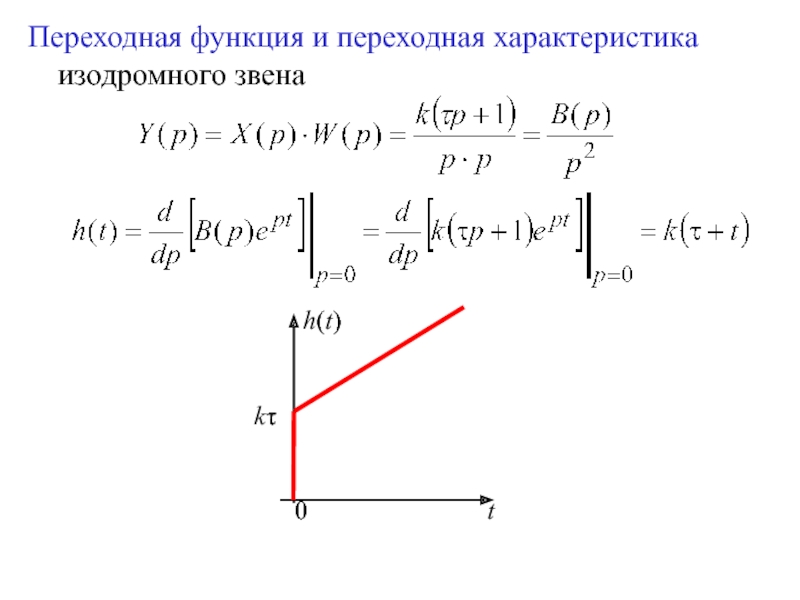
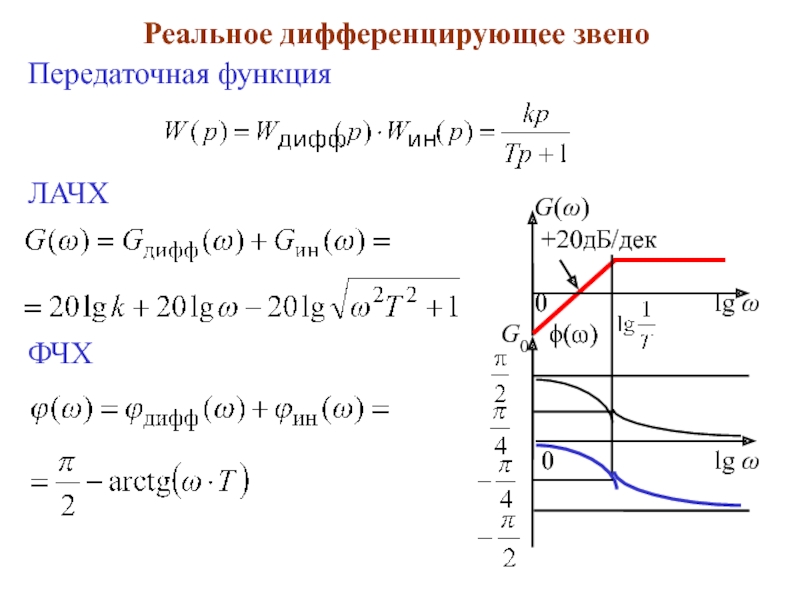
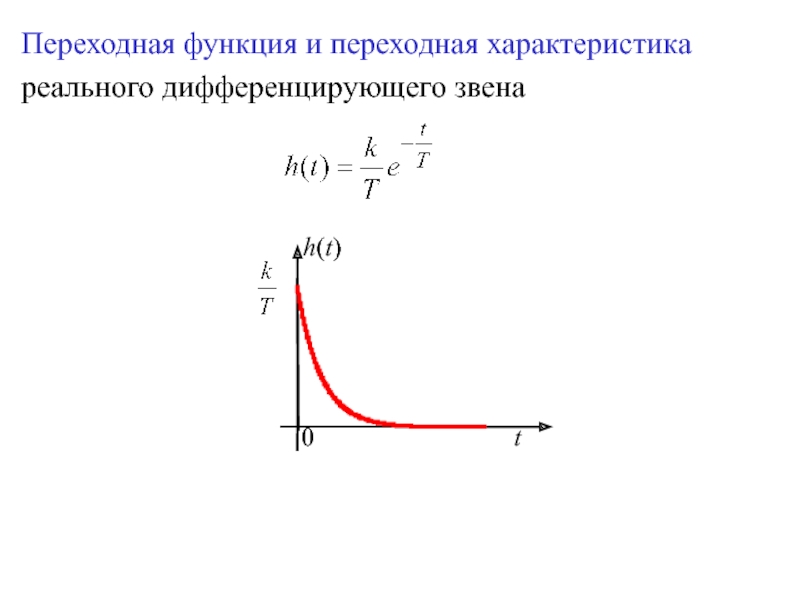






















![Блок №3 | [продолжение]
Чтобы сохранить вовлеченность, нам надо чтобы](/img/thumbs/ab172555748dd55bb91846e5ac965ffe-800x.jpg)
