Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1_05.ppt
Содержание
- 1. 1_05.ppt
- 2. Импульсное представлениеСпектр квантовой задачи является инвариантом, не
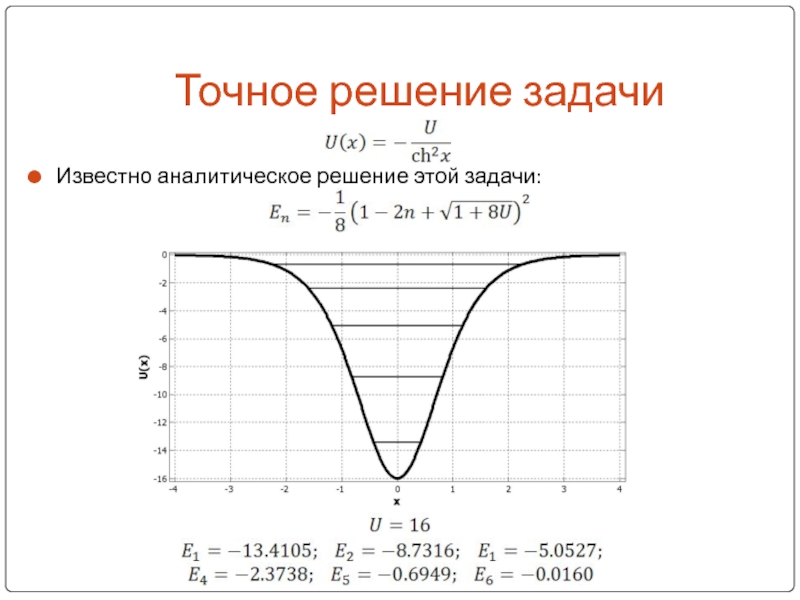
- 3. Точное решение задачиИзвестно аналитическое решение этой задачи:
- 4. Решение в координатном представленииРешение задачи в координатном представлении (случай конечной ямы):
- 5. Решение в импульсном представленииДля решения задачи в
- 6. Решение в импульсном представленииГамильтонова матрица в импульсном
- 7. Распределение по импульсам Спектр системы не зависит
- 8. Распределение по импульсам
- 9. Возврат в координатное представлениеЧтобы получить из собственных
- 10. Возврат в координатное представление
- 11. Скачать презентанцию
Импульсное представлениеСпектр квантовой задачи является инвариантом, не зависящим от выбора базисаИмпульсное представление – фурье-преобразование координатного пространстваБазис в импульсном представленииL – ширина ямы или ширина области, в которой локализован потенциал или волновые
Слайды и текст этой презентации
Слайд 1Импульсное представление. Распределение по импульсам.
Возврат в координатное представление
1.5. Потенциальная яма
в импульсном представлении
Слайд 2Импульсное представление
Спектр квантовой задачи является инвариантом, не зависящим от выбора
базиса
Импульсное представление – фурье-преобразование координатного пространства
Базис в импульсном представлении
L –
ширина ямы или ширина области, в которой локализован потенциал или волновые функции частицыФормально базис при построении гамильтоновой матрицы можно представить в виде
Единица означает, что соответствующая базисная функция описывает состояние частицы с импульсом k
Слайд 4Решение в координатном представлении
Решение задачи в координатном представлении (случай конечной
ямы):
Слайд 5Решение в импульсном представлении
Для решения задачи в импульсном представлении следует
записать гамильтониан в терминах импульсного базиса
Кинетическая энергия диагональна в импульсном
представлении:Слагаемое, отвечающее потенциальной энергии частицы, недиагонально:
Результат расчета практически не изменится, если последнее выражение рассчитать аналитически:
Слайд 6Решение в импульсном представлении
Гамильтонова матрица в импульсном представлении:
Матрица является плотной
Результатом
диагонализации будут собственные значения, являющиеся спектром системы, и собственные функции,
отвечающие этим собственным значениям, которые теперь будут зависеть не от координаты, а от импульса частицыЗначения импульса меняются от – π/h до π/h с шагом π/a
Слайд 7Распределение по импульсам
Спектр системы не зависит от представления, в
котором построена гамильтонова матрица. Решение задачи в импульсном представлении:
Собственные функции
зависят от представления, в котором построена гамильтонова матрица. После диагонализации матрицы будут получены собственные функции в импульсном представлении.Слайд 9Возврат в координатное представление
Чтобы получить из собственных функций в импульсном
представлении собственные функции в координатном представлении, необходимо выполнить обратное фурье-преобразование:
Для
четных собственных функций:Для нечетных собственных функций: