Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПИРАМИДА
Содержание
- 1. ПИРАМИДА
- 2. Париж.Новый вход в ЛуврСевастополь. Храм-пирамида.Париж.Новый проект.
- 3. Определения Евклид, пирамиду определяет как телесную фигуру,
- 4. А. М. Лежандр в 1794 году в
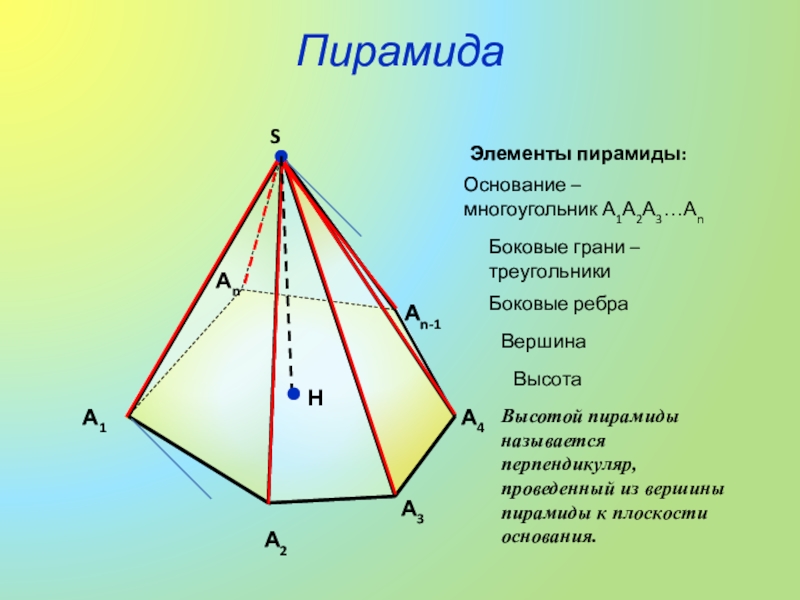
- 5. ПирамидаSЭлементы пирамиды:Основание – многоугольник А1А2А3…АnБоковые грани –
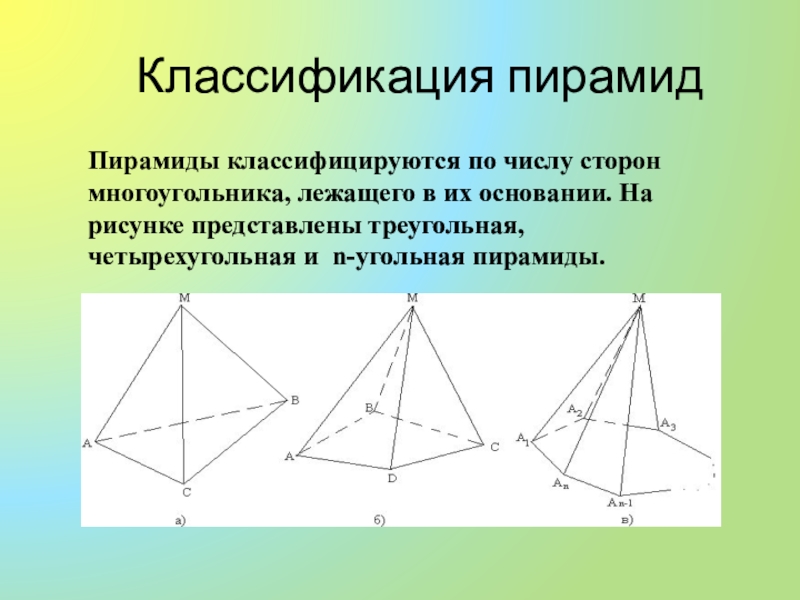
- 6. Классификация пирамидПирамиды классифицируются по числу сторон многоугольника,
- 7. Площадь поверхности пирамидыSпол = Sбок + SоснПлощадь боковой поверхности – сумма площадей боковых граней (треугольников)
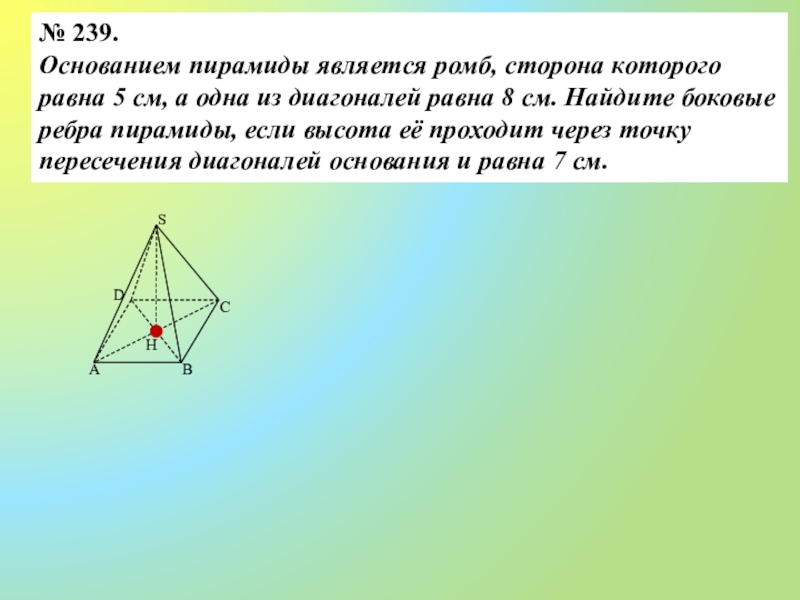
- 8. № 239. Основанием пирамиды является ромб, сторона
- 9. № 247 Двугранные углы при основании пирамиды
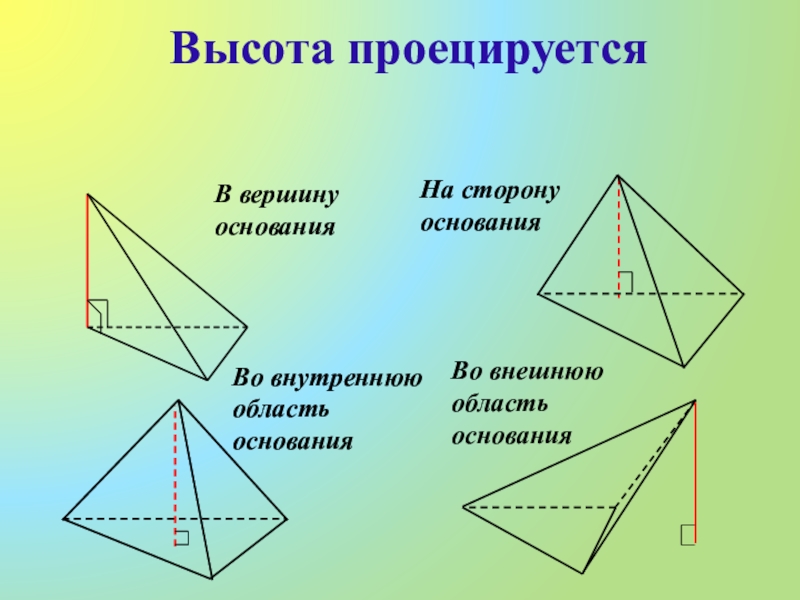
- 10. Высота проецируетсяВ вершину основанияНа сторону основанияВо внутреннюю область основанияВо внешнюю область основания
- 11. Скачать презентанцию
Париж.Новый вход в ЛуврСевастополь. Храм-пирамида.Париж.Новый проект.
Слайды и текст этой презентации
Слайд 3Определения
Евклид, пирамиду определяет как телесную фигуру, ограниченную плоскостями, которые
от каждойплоскости сходятся к одной точке.
пирамиды: “Это фигура, ограниченная треугольниками, сходящимися в одной точке и основанием которой служит многоугольник”.
Слайд 4А. М. Лежандр в 1794 году в своем труде “Элементы
геометрии” пирамиду определяет так: “Пирамида – телесная фигура, образованная треугольниками,
сходящимися в одной точке и заканчивающаяся на различных сторонах плоского основания”.
Слайд 5Пирамида
S
Элементы пирамиды:
Основание –
многоугольник А1А2А3…Аn
Боковые грани –
треугольники
Боковые ребра
Вершина
Высота
Высотой пирамиды
называется перпендикуляр, проведенный из вершины пирамиды к плоскости основания.
Слайд 6Классификация пирамид
Пирамиды классифицируются по числу сторон многоугольника, лежащего в их
основании. На рисунке представлены треугольная, четырехугольная и n-угольная пирамиды.
Слайд 7Площадь поверхности пирамиды
Sпол = Sбок + Sосн
Площадь боковой поверхности –
сумма площадей боковых граней
(треугольников)
Слайд 8№ 239.
Основанием пирамиды является ромб, сторона которого равна 5
см, а одна из диагоналей равна 8 см. Найдите боковые
ребра пирамиды, если высота её проходит через точку пересечения диагоналей основания и равна 7 см.
Слайд 9№ 247 Двугранные углы при основании пирамиды равны. Докажите: а) высота пирамиды
проходит через центр окружности, вписанной в основание;
O
Слайд 10Высота проецируется
В вершину основания
На сторону основания
Во внутреннюю область основания
Во внешнюю
область основания
