Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция_2_Выборочное_наблюдение.ppt
Содержание
- 1. Лекция_2_Выборочное_наблюдение.ppt
- 2. 2Выборочное наблюдениеПод выборочным наблюдением понимается такое несплошное
- 3. 3Выборочное наблюдение
- 4. 4Ошибка выборочного наблюденияОшибка выборочного наблюдения – представляет
- 5. 5Теорема П.Л.ЧебышеваПри достаточно большом числе независимых наблюдений
- 6. 6Теорема А.М.ЛяпуноваРаспределение выборочных средних (а следовательно, и
- 7. 7Теорема А.М.ЛяпуноваЗначение интеграла F(t) для различных значений
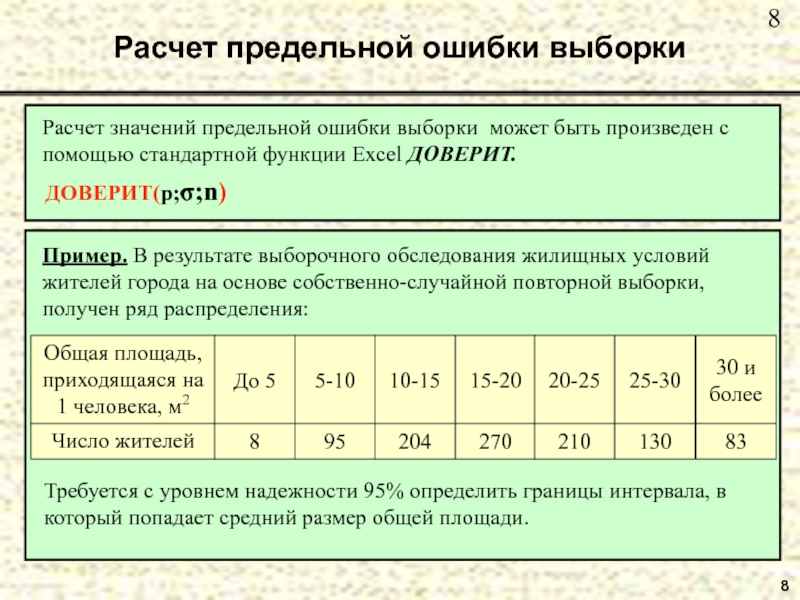
- 8. 8Расчет предельной ошибки выборки
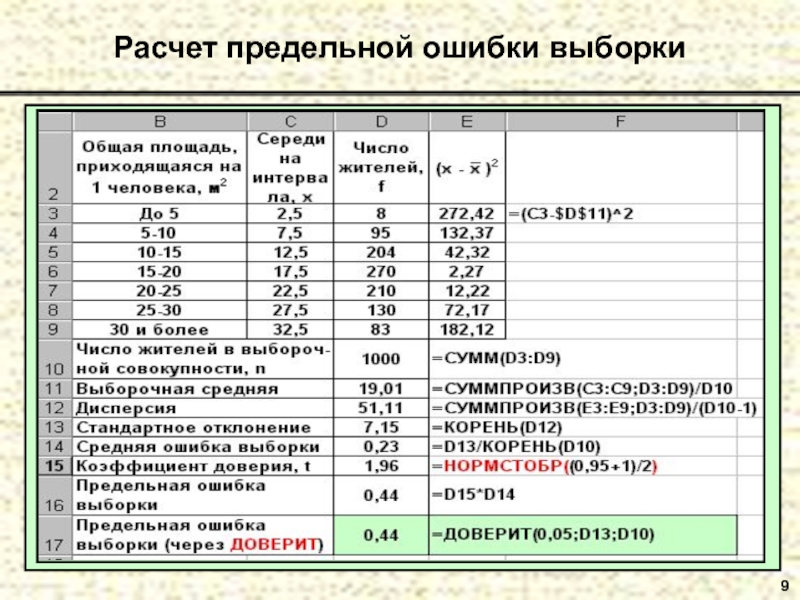
- 9. 9Расчет предельной ошибки выборки
- 10. 10Теорема Бернулли
- 11. 11Теорема Бернулли
- 12. 12Уточнение формулы средней ошибки выборки
- 13. 13Уточнение формулы средней ошибки выборкиДля приведенного выше
- 14. 14Предельная ошибка альтернативного признакаДля приведенного выше примера,
- 15. 15Способы формирования выборочной совокупностиПо виду отбора
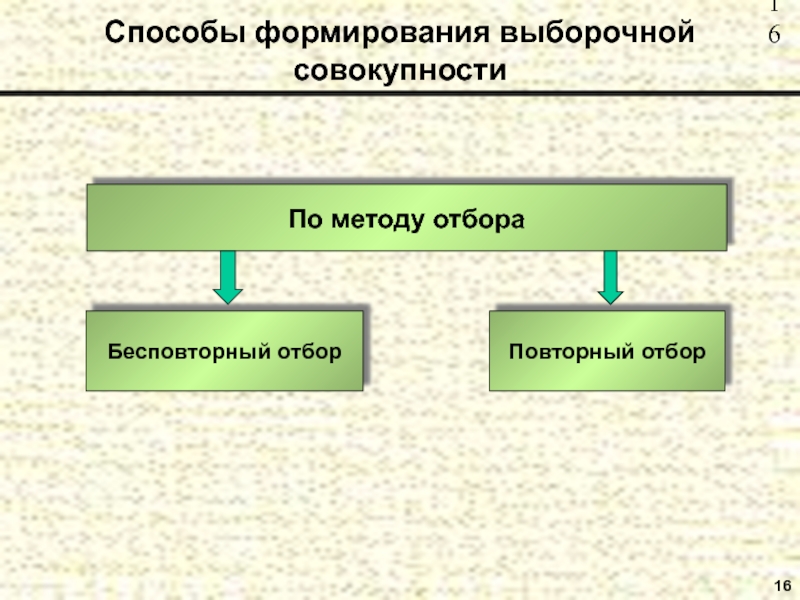
- 16. 16Способы формирования выборочной совокупностиПо методу отбора
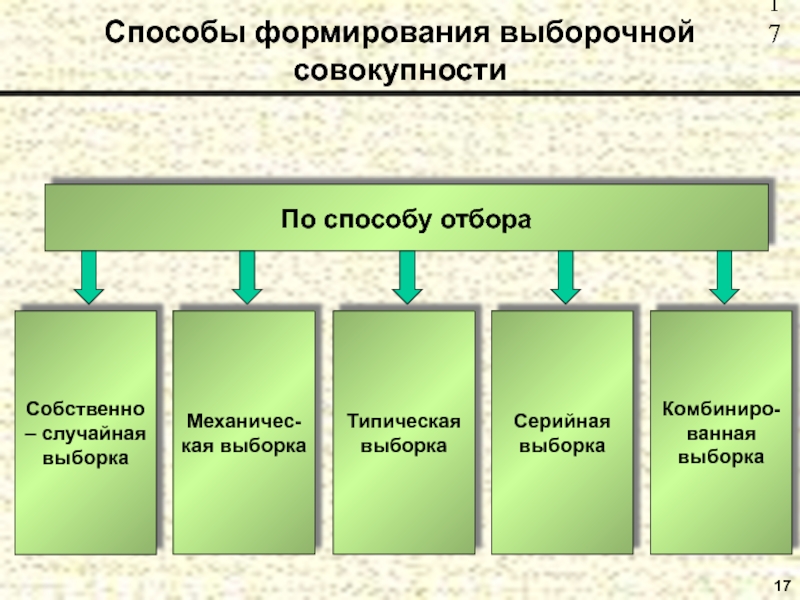
- 17. 17Способы формирования выборочной совокупностиПо способу отбора
- 18. Типическая выборка18
- 19. Типическая выборка19Пример. 10%-ный бесповторный типический отбор рабочих
- 20. 20Типическая выборка1. Расчет пропорционально объему типических групп.
- 21. 21Типическая выборка2. Расчет пропорционально дифференциации признака.
- 22. 22Серийная выборкаСредняя ошибки выборки:повторный отборбесповторный отборМежгрупповая дисперсия:
- 23. Определение необходимого объема выборки23
- 24. 24Определение необходимого объема выборки
- 25. 25Определение необходимого объема выборки
- 26. 26Определение необходимого объема выборкиПример 3. В фермерских
- 27. 27Определение необходимого объема выборкиПример 4. На склад
- 28. 28Малая выборка Распределение СтьюдентаПод малой выборкой понимается
- 29. 29Способы нахождения критерия Стьюдента.1. С помощью таблиц распределения Стьюдента (t - распределение): Малая выборка Распределение Стьюдента
- 30. 30Малая выборка Распределение Стьюдента
- 31. 31Малая выборка Распределение СтьюдентаПример. При контрольной проверке
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 22
Выборочное наблюдение
Под выборочным наблюдением понимается такое несплошное наблюдение, при котором
статистическому обследованию (наблюдению) повергаются единицы изучаемой совокупности, отобранные случайным образом.
Совокупность
отобранных для обследования единиц в статистике принято называть выборочной, а совокупность единиц, из которых производится отбор, - генеральной. Слайд 44
Ошибка выборочного наблюдения
Ошибка выборочного наблюдения – представляет собой разность между
величиной параметра в генеральной совокупности и его величиной, вычисленной по
результатам выборочного наблюдения.Слайд 55
Теорема П.Л.Чебышева
При достаточно большом числе независимых наблюдений с вероятностью, близкой
к единице, можно утверждать, что отклонение выборочной средней от генеральной
будет сколь угодно малым. При этом величина предельной ошибки выборки не должна превышать tμ.Слайд 66
Теорема А.М.Ляпунова
Распределение выборочных средних (а следовательно, и их отклонений от
генеральной средней) при достаточно большом числе независимых наблюде-ний приближенно нормально
при условии, что генеральная совокупность об-ладает конечной средней и ограниченной дисперсией.Предельная ошибка выборки дает возможность выяснить, в каких преде-лах находится величина генеральной средней.
Слайд 77
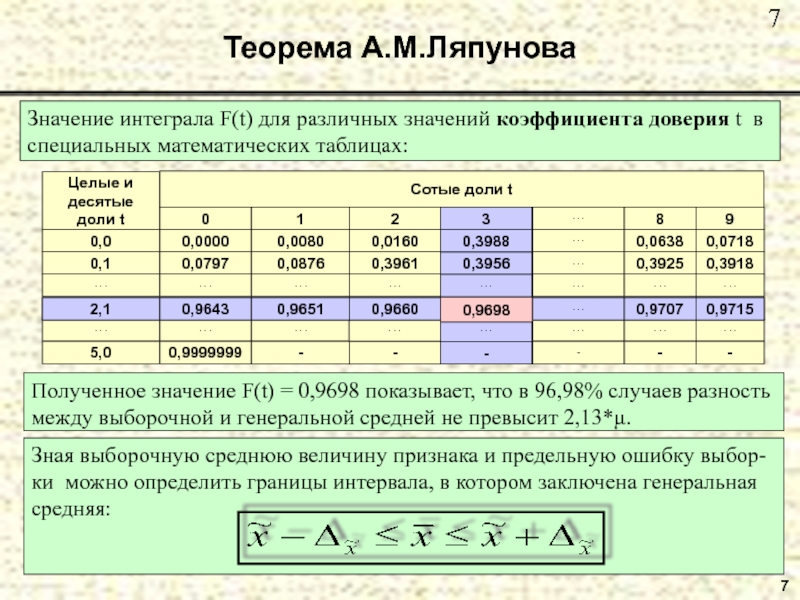
Теорема А.М.Ляпунова
Значение интеграла F(t) для различных значений коэффициента доверия t
в специальных математических таблицах:
Полученное значение F(t) = 0,9698 показывает,
что в 96,98% случаев разность между выборочной и генеральной средней не превысит 2,13*μ. Слайд 1313
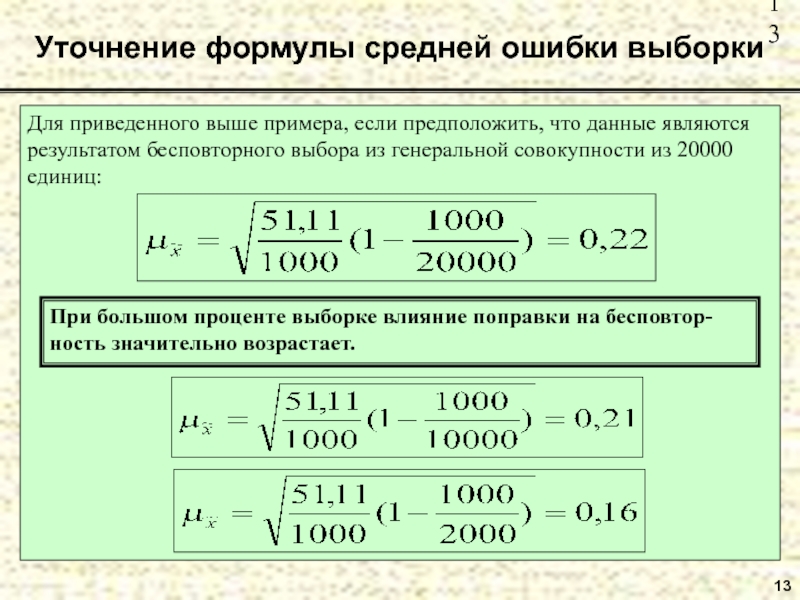
Уточнение формулы средней ошибки выборки
Для приведенного выше примера, если предположить,
что данные являются результатом бесповторного выбора из генеральной совокупности из
20000 единиц:При большом проценте выборке влияние поправки на бесповтор-ность значительно возрастает.
Слайд 1414
Предельная ошибка альтернативного признака
Для приведенного выше примера, определим предельную ошибку
выборки для лиц, обеспеченность жильем которых составляет менее 10 м2.
1.
Выборочная доля:Слайд 19Типическая выборка
19
Пример. 10%-ный бесповторный типический отбор рабочих предприятия, пропорциональный размерам
цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности, привел
к следующим результатам:Необходимо определить пределы среднего числа дней временной нетрудоспособности одного рабочего в целом по предприятию.
Слайд 2222
Серийная выборка
Средняя ошибки выборки:
повторный отбор
бесповторный отбор
Межгрупповая дисперсия:
Слайд 2626
Определение необходимого объема выборки
Пример 3. В фермерских хозяйствах области 10
000 коров. Из них в районе А – 5000, в
районе Б – 3000, в районе В - 2000. Чтобы определить средний надой предполагается провести типическую выборку коров с про-порциональным отбором внутри групп (механическим). Какое количество коров следует отобрать, чтобы с вероятностью 0,954 ошибка выборки не превышала 5 л, если на основе предыдущих обследований известно, что дисперсия типической выборки равна 1600?Слайд 2727
Определение необходимого объема выборки
Пример 4. На склад поступило 100 ящиков
деталей по 80 шт. в каждом. Для установления среднего веса
деталей следует провести серийную вы-борку деталей методом механического отбора так, чтобы с вероятностью 0,954 ошибка выборки не превышала 2 г. На основе предыдущих обследо-ваний известно, что дисперсия серийной выборки равна 4. Определить не-обходимый объем выборки.Методики, разработанные в рамках конкретных обследований и опре-деленных способов формирования выборочной совокупности, требу-ют дальнейшего теоретического обоснования и практической провер-ки.