2. Кинематический анализ.PPT

с к и й а н а л и

з –
это исследование расчётной схемы
сооружения (системы), выполняемое
до начала расчёта с целью определения кинематического качества системы (геометрической неизменяемости, мгновенной изменяемости или
геометрической изменяемости), а в случае
геометрической неизменяемости системы – также для выявления её статической определимости или неопределимости.

часть системы (один или несколько
соединённых друг с другом элементов),

форма и размеры которой могут изменяться
только вследствие деформации материала.

С в я з и (механические) –
ограничения на перемещения
(линейные и/или угловые) точек или сечений элементов системы, а также устройства, технически реализующие эти ограничения.

С т е п е н и с в о б о д ы –
независимые геометрические параметры,
полностью определяющие положение
всех точек диска или системы в целом
при их возможных перемещениях.

– диски из одного элемента
(а, б, в – стержни

с прямолинейной, криволинейной и ломанной в плоскости
или в пространстве осью; г – диск-пластинка; д – диск-оболочка);
– е, ж, з, и, к – диски из нескольких элементов
(е, ж, з – из однотипных элементов – стержней, плоские (е, ж) и пространственный (з);
и, к – комбинированные пластинчато- и оболочечно-стержневые, пространственные).

(распределённые по объёму,

поверхности или линии)

– по соединяемым дискам

внутренние
внешние

– по числу ограничиваемых
перемещений

простые (линейные и угловые)
сложные

– по физическим свойствам

жёсткие (недеформируемые)
податливые (деформируемые)

– по кинематическому
признаку

необходимые
избыточные (лишние и ложные)

–
это система, перемещения в которой могут возникать
только вследствие деформации

её элементов.

Геометрически изменяемой
называется система (ГИС), в которой возможны
конечные перемещения без деформации элементов.

Мгновенно изменяемой
называется система (МИС), в которой
могут возникать бесконечно малые перемещения
без деформации её элементов.

2) качественный (структурный) анализ.

К о л и ч е с

т в е н н ы й а н а л и з –
это исследование расчётной схемы сооружения,
заключающееся в оценке баланса (соотношения)
суммарного числа nΔ степеней свободы дисков системы
до наложения на них внешних и внутренних связей
(т.е. несвязанных дисков) и суммарного числа nc
внешних и внутренних связей системы,
в пересчёте на связи первого типа.

Необходимое условие
геометрической неизменяемости системы:

( W = nΔ – nc )

н н ы й а н а л и

з

( W = nΔ – nc )

Необходимое условие геометрической неизменяемости системы:

Для плоской системы:
nΔ = 3D; nc = nвнут. св. + nвнеш. св. = 3П + 2H + C + C0
D – количество дисков;
П – число простых припаек
Н – число простых шарниров
С – количество внутренних связей первого типа ( линейных и угловых );
С0 – число внешних ( опорных ) связей – в пересчёте на связи первого типа.

между дисками системы,
без учёта диска «земля»;

nвнут. cв.

nвнеш. cв.

Простая припайка – жёсткое соединение двух дисков.
Простой шарнир ( цилиндрический или поступательный ) – шарнирное соединение двух дисков.

Сложная ( кратная ) припайка

Сложный ( кратный ) шарнир

Соответствующее
( жёсткое или шарнирное )
соединение более чем двух дисков

Учитываются эквивалентным числом простых припаек ( шарниров ):

П = nD – 1

H = nD – 1

nD – число соединяемых дисков в узле

W = 3D – ( 3П + 2H + C + C0 )

заключающееся
в проверке правильности расположения связей, выявлении возможных дефектов соединения

дисков и завершающееся определением кинематического качества (природы) системы (её геометрической неизменяемости, изменяемости или мгновенной изменяемости).

о д и м ы е с в я

з и – это связи, удаление которых
вызывает изменение кинематической природы системы
(геометрически неизменяемая система превращается
в геометрически изменяемую или мгновенно изменяемую,
мгновенно изменяемая система становится
геометрически изменяемой).
Л и ш н и м и называются связи, при удалении которых
кинематическая природа системы не изменяется, но эти связи ограничивают перемещения в деформируемой системе.
Л о ж н ы е с в я з и – такие, которые не оказывают
никакого влияния ни на кинематическую природу системы,
ни на перемещения в ней, определяемые с учётом
деформации элементов.

Избыточные
связи

δS – возможное перемещение в системе с удалённой связью по направлению этой связи (без учёта деформаций);
– то же, с учётом деформаций элементов системы.

определимой составной системы:
для определения реакций связей рассматривается равновесие частей,
начиная

с самой второстепенной и заканчивая главной
(то есть в порядке, обратном последовательности синтеза).

Если в процессе синтеза системы на нескольких шагах (более одного) последовательно образуются геометрически неизменяемые системы, то рассматриваемая система может квалифицироваться как составная, с выделением в ней главных и второстепенных частей.

Главной называется геометрически неизменяемая часть
составной системы, способная воспринимать любые воздействия
даже при отсутствии всех других частей.

Второстепенная часть составной системы – это часть, утрачивающая работоспособность вследствие возникновения
её геометрической или мгновенной изменяемости
при удалении других частей (всех или некоторых).

Второстепенные части могут образовывать иерархию по признаку
большей-меньшей второстепенности.
Самой второстепенной частью является та, которая неработоспособна
при отсутствии любой другой части системы.

Замечание: понятия составной системы, главной и второстепенной частей, а также соображения о последовательности расчёта не относятся непосредственно к кинематическому анализу ; принципиально важными они являются для статически определимых систем.

система геометрически неизменяемой?
2) если да, то статически определима она или

статически неопределима?

g

7 ( диски D5 и D6 – стержни

с ломаными осями)
П = 1 (между дисками D3 и D4
в узле f )
Н = 6 (простые – в узлах e, g, c, f,
кратный – в узле h )
С = 2 ( стержни ed и kp )
С0 = 4 (шарнирные неподвижные
опоры А и В )

p

Связь
1-го типа

Связь
1-го типа

W = 3*7 – (3*1+2*6+2+4) = 21 – 21 = 0 –
необходимое условие геометрической неизменяемости выполняется.
В ы в о д: система может быть геометрически неизменяемой.

проверка выполнения необходимого, но недостаточного условия геометрической неизменяемости системы

1: соединение двух дисков (D1 и D2 ) по способу

2б –
с помощью шарнира g и линейной связи ed, ось которой не проходит через центр шарнира. Результат – диск DI : DI = D1 + D2 (по способу 2б).

Вариант:
соединение трёх дисков
(D1 ,D2 и диск ed) по способу 3б – с помощью трёх цилиндрических шарниров
в точках e, d и g, не лежащих
на одной прямой.
Результат – диск DI :
DI = D1 + D2 + ed
(по способу 3б).

2: соединение трёх дисков ( DI , cfB и диск

«земля» ) по способу 3б –
с помощью трёх цилиндрических шарниров в точках A, c и B,
не лежащих на одной прямой.
Результат – диск DII :
DII = DI + cfB + «земля»
(по способу 3б) .

Примечание:
поскольку в диск DII
входит диск «земля»,
то DII является
геометрически
неизменяемой
системой:

c

A

DII

f

B

«з е м л я»

3: соединение трёх дисков ( DII , D5 и D6

) по способу 3б –
с помощью трёх цилиндрических шарниров в точках e, h и f,
не лежащих на одной прямой.
Результат – диск DIII :
DIII = DII + D5 + D6
(по способу 3б) .

Примечание:
поскольку в диск DIII
входит диск «земля»,
то DIII является
геометрически
неизменяемой
системой:

c

f

A

B

DII

DIII

D5

h

D6

«з е м л я»

4: соединение двух дисков ( DIII и D7 ) по

способу 2б – с помощью
цилиндрического шарнира в точке h и линейной связи ed, ось которой
не проходит через центр шарнира.
Результат – диск DIV :
DIV = DIII + D7 (по способу 2б) .

Примечание:
поскольку в диск DIV входит диск «земля», то DIV
является геометрически неизменяемой системой:

c

f

A

B

DII

D5

D6

k

DIV

Варианты:
а) соединение трёх дисков
(DIII ,hk и kp) по способу 3б –
с помощью трёх цилиндрических шарниров
h, k и p, не лежащих
на одной прямой;
б) присоединение точки k
к диску DIII по способу 1 –
с помощью двух связей
1-го типа (hk и kp).

DIII

h

p

D7

«з е м л я»

о д :
система
геометрически
неизменяемая
и
статически
определимая.

а) в системе имеется достаточное

число связей, избыточных связей нет (W = 0); б) структура системы правильная – отсутствуют дефекты расположения связей.

g

связей рассматривается
равновесие частей
системы, начиная
с самой второстепенной
и

заканчивая главной:
ВЧ2 ВЧ1 ГЧ
(то есть в порядке,
обратном
последовательности
синтеза).

Главная
часть
(ГЧ)

ВЧ1

ВЧ2

Второстепенные
части

g

Поскольку в процессе синтеза системы на нескольких шагах (более одного) последовательно образуются геометрически неизменяемые системы (ГНС1 , ГНС2 , ГНС), то рассматриваемая система может квалифицироваться как составная, с выделением в ней главной и второстепенных частей:

выполнен
с использованием только типовых способов
(приёмов) геометрически неизменяемого
соединения дисков, называются

системами с простой структурой.

Системы, для которых качественный
(структурный) анализ расчётной схемы
не может быть полностью выполнен
с использованием только типовых способов
(приёмов) геометрически неизменяемого
соединения дисков, называются
системами со сложной структурой.

В качественном анализе систем со сложной структурой применяются:
– исследование кинематической природы связей ( всех или части ) по критерию ;
– проверка по аналитическому признаку геометрической неизменяемости ;
– способ замены связей.

П = 0; H = 3; C = 2; C0

= 7

W = 3*D – ( 3*П + 2*H + C + C0 ) =
= 3*5 – ( 3*0 + 2*3 + 2 + 7 ) = 0 –
необходимое условие геометрической неизменяемости выполняется;
система может быть геометрически неизменяемой

системы с помощью типовых способов геометрически неизменяемого соединения дисков не

удаётся,
поэтому исследуется кинематическая природа связей системы:
удаляется стержень АВ, который может рассматриваться
как линейная связь 1-го типа

Направление

удалённой
связи

В результате удаления связи
система превращается в механизм,
которому задаётся возможное перемещение

А

В

связи –
в данном случае проекция взаимного (относительного)
линейного перемещения

точек А и В по направлению
оси удалённой линейной связи

Этап 2. Качественный (структурный) анализ

Направление

удаленной
связи

δS,l

δS,r

δS = δS,l + δS,r = 0

Вывод: удалённая связь – необходимая, следовательно, структура системы правильная,
система геометрически неизменяемая.

Можно
использовать
план
перемещений
узлов:

С

К

0

В

А

С, K

α

α

α

α

δS,l

δS,r

δS

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 29» )
1. Что такое кинематический анализ? Его назначение? ( 2 )
2. Назовите основные понятия кинематического анализа. ( 3 )
3. Дайте определение диска. ( 3 ) 3. Дайте определение диска. ( 3 ) Что может быть диском? ( 4 )
4. Что такое диск «земля» и какими свойствами он наделяется? ( см. [1] )
5. Дайте определение связи. ( 3 )) По каким признакам и как классифицируются связи? ( 5 )
6. Перечислите типы связей плоских систем и для каждого из них
дайте кинематическую и статическую характеристики. ( 6 )
7. Каким комбинациям простых связей кинематически эквивалентны
сложные связи разных типов? ( см. [1] )
8. Дайте разные варианты изображения связей плоских систем. ( 6 )
9. Какова роль гипотезы отвердения материала в кинематическом анализе? ( см. [1] )
10. Что такое степени свободы ( 3 ) и какие величины могут выступать в качестве
степеней свободы? ( 8 )
11. Сколько степеней свободы имеет жёсткий диск в пространстве и в плоскости?
А точка? ( 8 )
12. Ответы на какие главные вопросы даются в ходе кинематического анализа? ( 17 )
13. Какие системы называются геометрически неизменяемыми?
Геометрически изменяемыми? Мгновенно изменяемыми? ( 9 )
14. Назовите этапы кинематического анализа. ( 11 )
15. Дайте определение количественного анализа. ( 11 )
16. Что означают символы nΔ и nc ( 11 ) и как вычисляются обозначаемые ими
величины? ( 12 )
17. Какие припайки (шарниры) называются сложными ( кратными )?
Как определяется число эквивалентных им простых припаек ( шарниров )? ( 12 )
_______________________________________________
*) Только в режиме «Показ слайдов»

[1] Себешев В.Г. Кинематический анализ сооружений : Учеб. пособие /
Новосибирск: НГАСУ (Сибстрин), 2006. – 58 с.

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 30» )
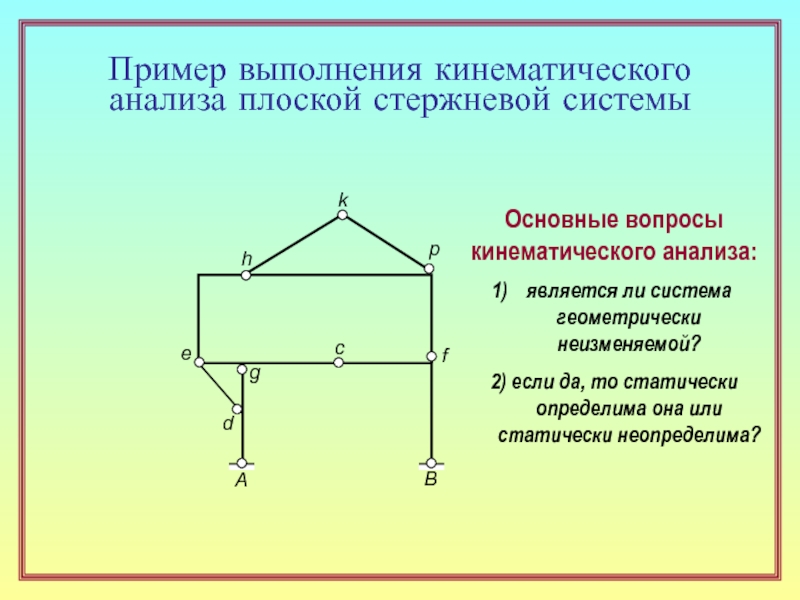
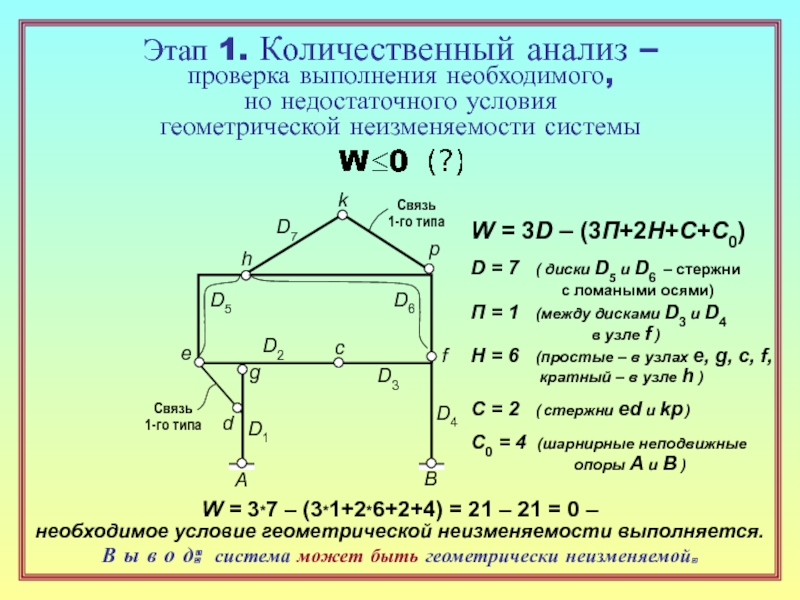
18. Какой вид имеет необходимое условие геометрической неизменяемости системы? ( 11 )
19. Почему оно является недостаточным? ( см. [1] )
20. Что такое W ? Как вычисляется эта характеристика? ( 12 )
21. Какой вывод делается по результатам кинематического анализа, если получается
W > 0 ? ( см. [1] ) А если необходимое условие неизменяемости выполняется? ( 18 )
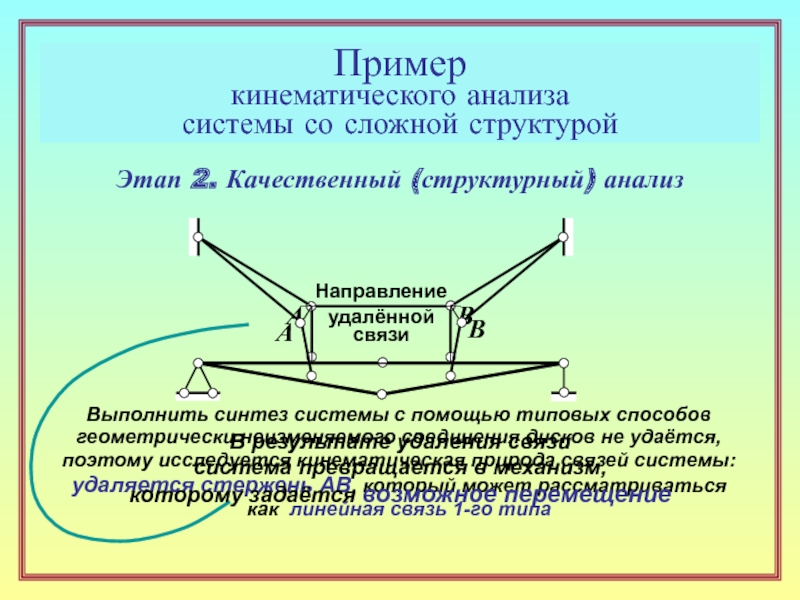
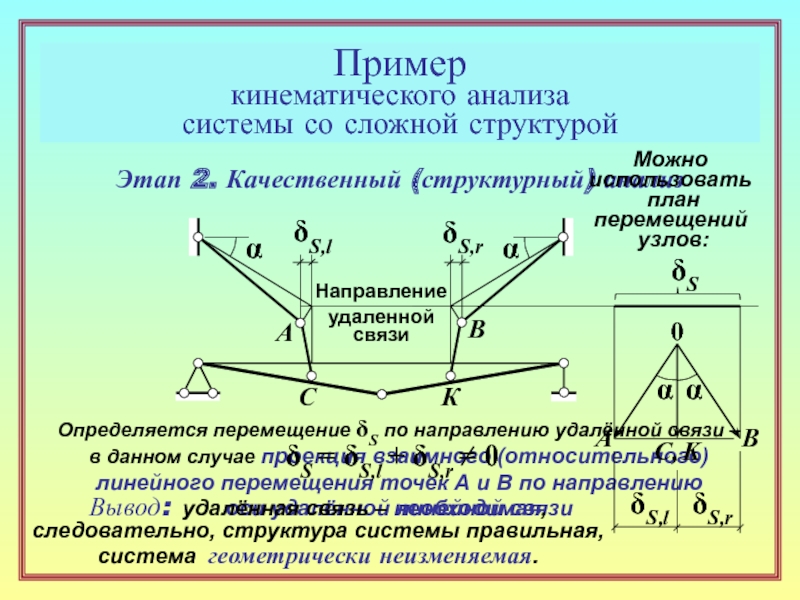
22. Что такое качественный ( структурный ) анализ? ( 13 )
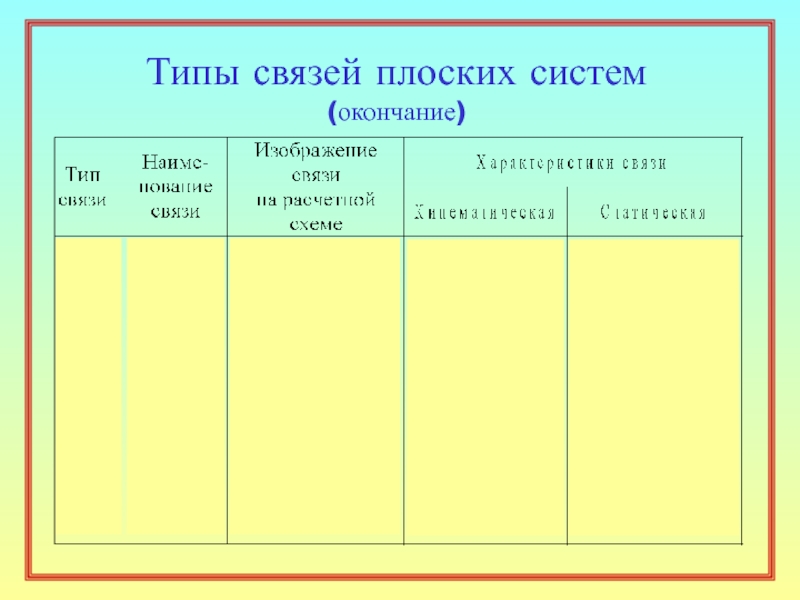
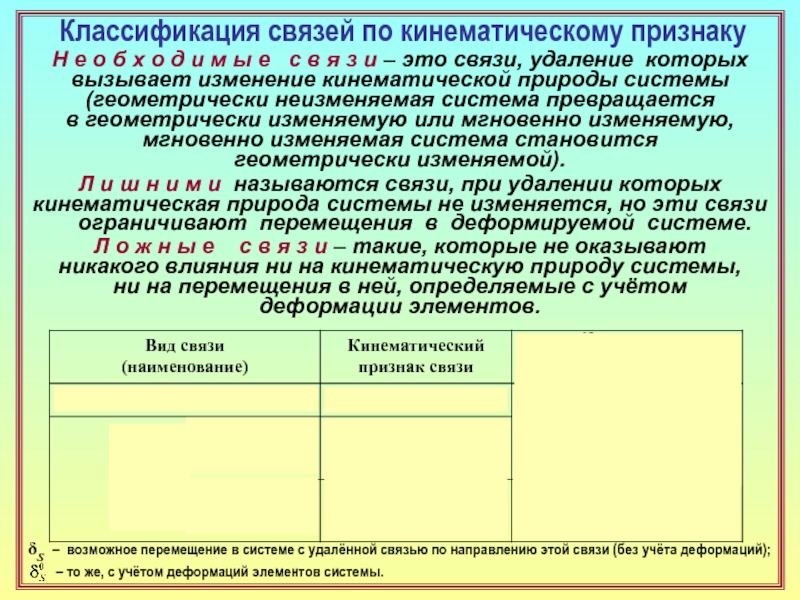
23. Как классифицируются простые связи по кинематическому признаку? ( 14 )
24. Дайте определения необходимой, лишней и ложной связей. ( 14 )
25. Какие геометрические параметры используются в описании кинематических признаков
разных связей? ( 14 )
26. Что общего у необходимых и лишних связей? У лишних и ложных связей?
В чём различия между ними? ( 14 ) Что нужно делать с обнаруженными ложными
связями? ( см. [1] )
27. Как выявляются лишние связи? ( см. [1] )
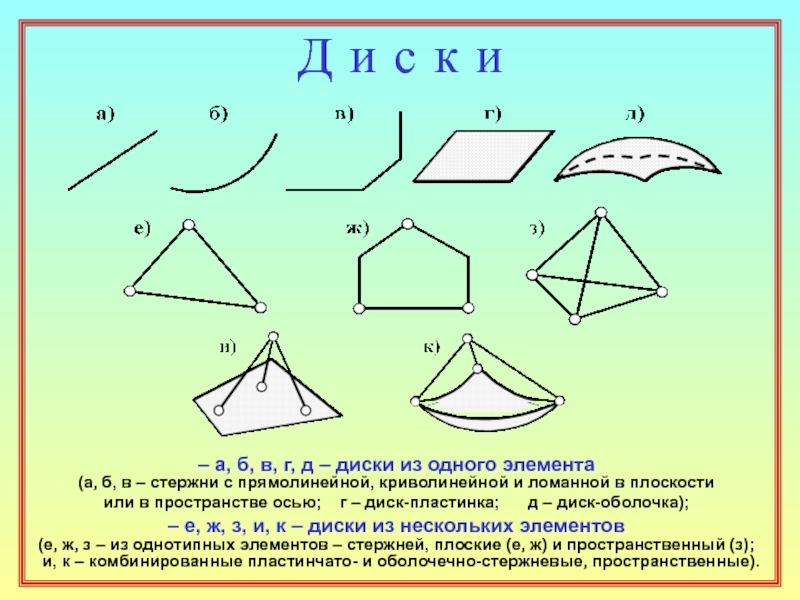
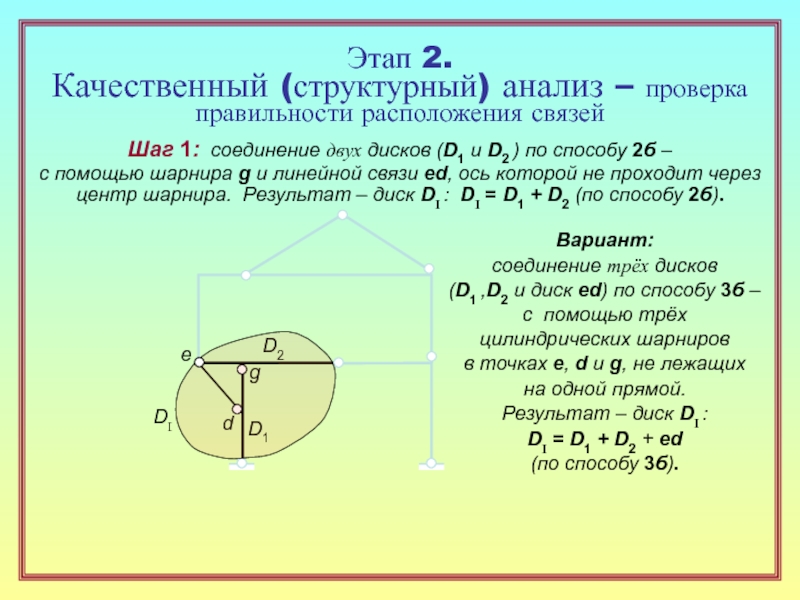
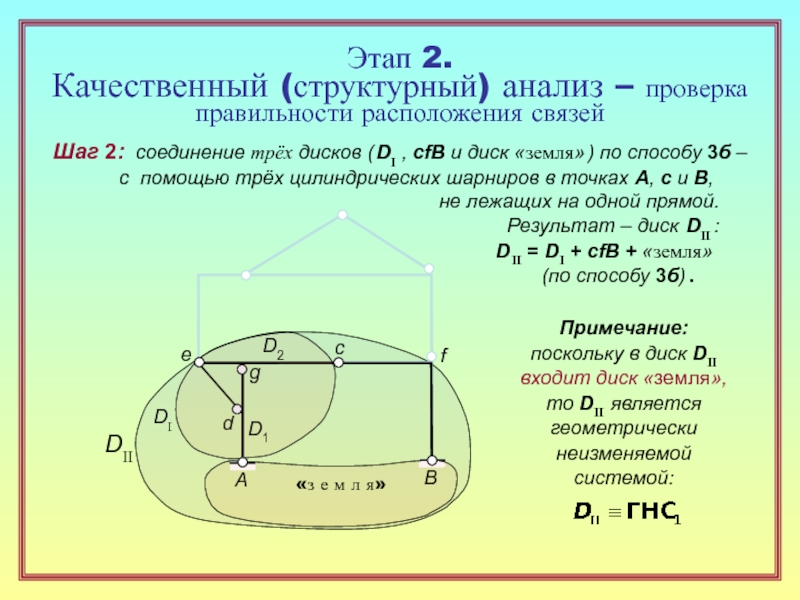
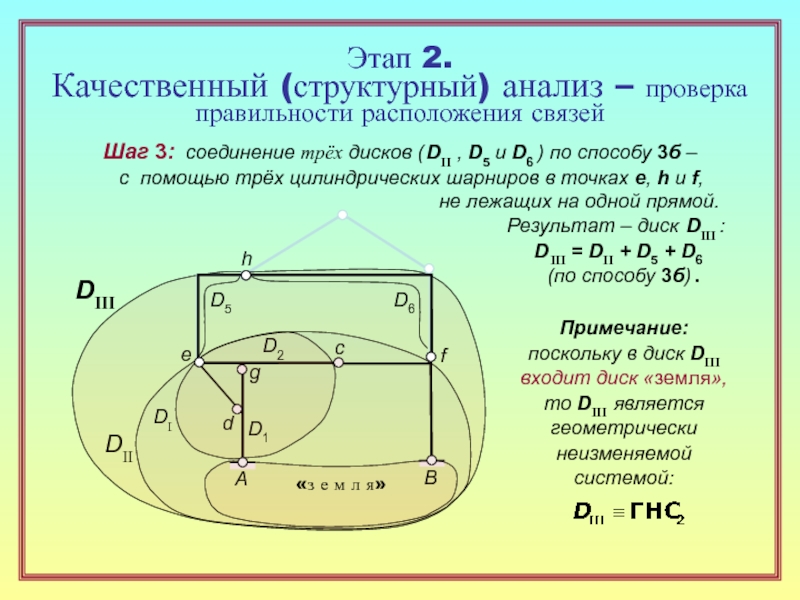
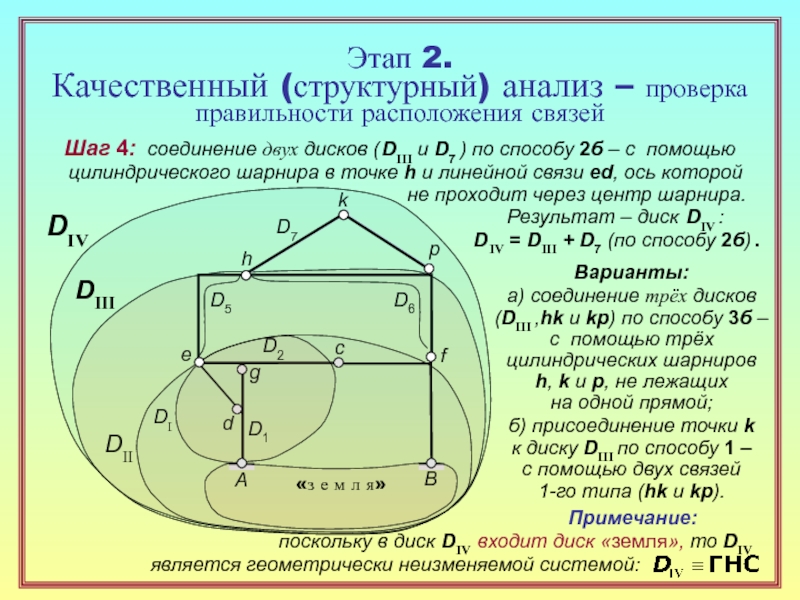
28. Перечислите типовые способы геометрически неизменяемого соединения дисков,
объясните смысл каждого из них с указанием требований к расположению связей. ( 15 )
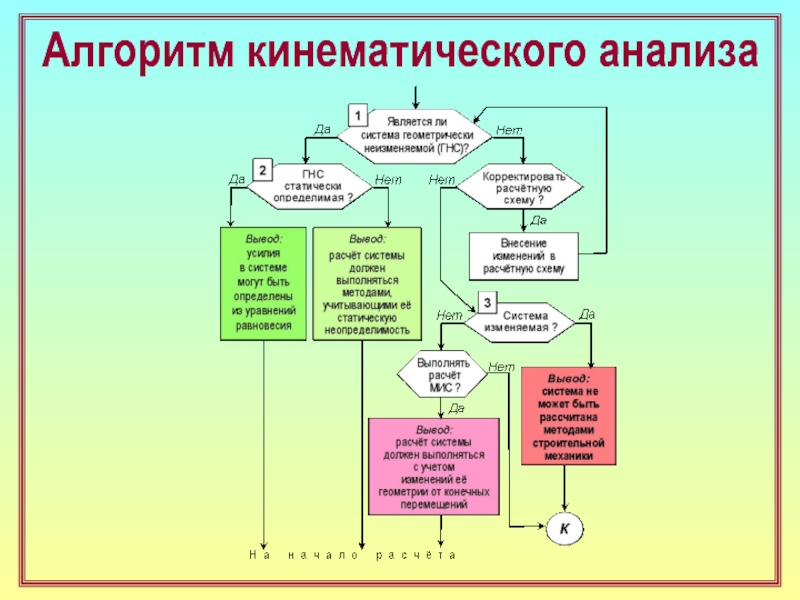
29. Какова последовательность действий при выполнении структурного анализа
с применением типовых способов соединения дисков? ( см. [1] )
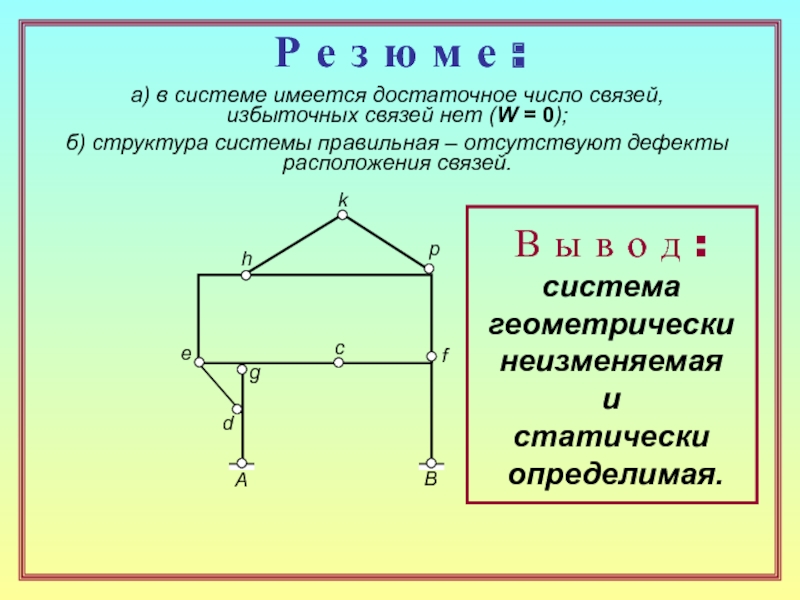
30. Какие выводы делаются по результатам структурного анализа системы? ( 23 )
31. Что такое система с простой структурой? ( 25 )
32. Что такое система со сложной структурой? Каковы возможные пути выполнения
структурного анализа таких систем? ( 25 )
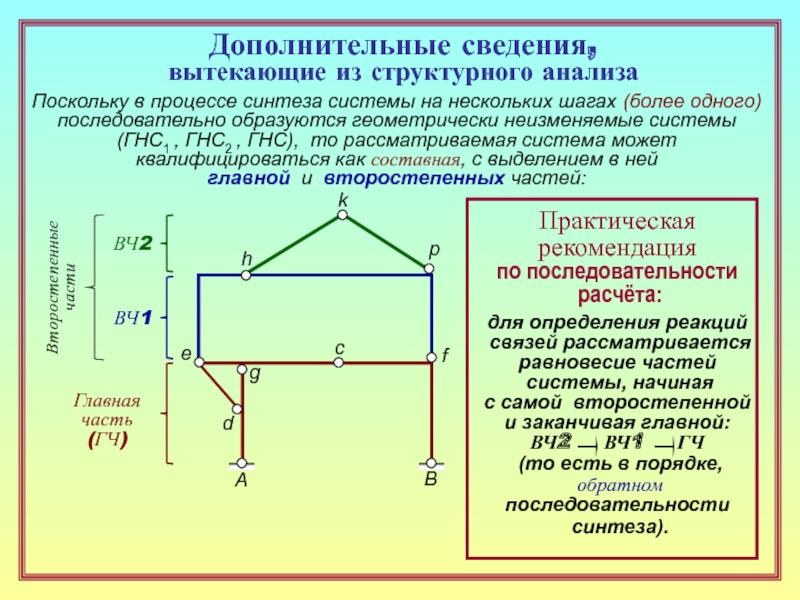
33. Какие части составной системы называются главными,
а какие – второстепенными? ( 16 )
____________________________________________________________
*) Только в режиме «Показ слайдов»

[1] Себешев В.Г. Кинематический анализ сооружений : Учеб. пособие /
Новосибирск: НГАСУ (Сибстрин), 2006. – 58 с.