Слайд 1Статистическое исследование
Этап 2. Первичное обобщение и группировка статистических данных.
кумуляты
(огивы), графики распределения частот (частостей).
Формирование рядов динамики и их первичный
анализ.
Расчет моментов К-го порядка (средних, дисперсий, мер скошенности, измерения эксцесса) с целью определения показателей центра расширения показателей вариации, показателей скошенности (асимметрии), показателей эксцесса (островершинности).
Формирование и первичные расчеты сложных статистических показателей (относительных, сводных многоуровневых).
Формирование и первичные расчеты индексных показателей.
Слайд 2
Статистическое исследование
15. Диаграммы.
Слайд 3Диаграмма
Наиболее распространенным способом графического изображения статистической информации являются диаграммы.
По содержанию
они подразделяются на:
диаграммы сравнения,
структурные,
динамические,
графики
связи,
графики контроля и др.
Слайд 4Диаграмма
По форме диаграммы принято подразделять на следующие виды:
столбиковые
диаграммы;
полосовые диаграммы;
круговые диаграммы;
линейные диаграммы;
фигурные диаграммы;
Слайд 5Диаграмма
Диаграммы сравнения отражают соотношения различных исследуемых объектов в связи с
каким-либо экономическим показателем. Самыми удобными графиками, на которых осуществляется сопоставление
величин экономических показателей, являются столбиковые и полосовые диаграммы. Для изображения таких диаграмм применяется прямоугольная система координат. На оси абсцисс графиков столбиковых диаграмм помещается основа для определенных столбцов одинакового размера для всех исследуемых объектов. Высота каждого их столбцов должна выражать величину того экономического показателя, который отражен в определенном масштабе на оси ординат.
Полосовые диаграммы, в отличие от столбиковых, изображают по горизонтали: основа полос располагается на оси ординат, а экономические показатели в определенном масштабе — на оси абсцисс.
Слайд 6Диаграмма
Структурные (секторные) диаграммы дают возможность представить состав исследуемых экономических показателей
и долю (удельный вес) конкретных частей в совокупной сумме экономического
показателя.
В рассматриваемых диаграммах экономические явления представляются как определенные геометрические фигуры (круги или квадраты), которые разбиты на несколько секторов. Площадь круга или квадрата принимается равной ста процентам либо единице. Площадь же любого данного сектора характеризуется долей рассматриваемой части в составе ста процентов или единицы.
Слайд 7Диаграмма
Динамические диаграммы характеризуют динамику, то есть изменения
количественной оценки данного экономического явления в течение известных периодов времени.
С этой целью могут применяться любые из рассмотренных видов диаграмм (столбиковые, полосовые, круговые, квадратные, фигурные). Вместе с тем чаще всего здесь используются линейные диаграммы (графики). На таких диаграммах изменение количественной оценки экономического явления изображается определенной линией, которая выражает непрерывность происходящего процесса.
На оси абсцисс линейного графика изображаются определенные периоды времени, а на оси ординат — соответствующие величины данного экономического явления за рассматриваемые периоды времени в соответствии с принятым числовым масштабом.
Слайд 8Диаграмма
Линейные графики (диаграммы) применяются также и при изучении взаимосвязей между
отдельными экономическими показателями. В этом случае их можно рассматривать как
графики связи. В графиках связи ось абсцисс содержит числовые значения какого-либо фактора, а ось ординат — числовые значения результирующего показателя. Подобные графики характеризуют тенденцию и форму связи между экономическими показателями.
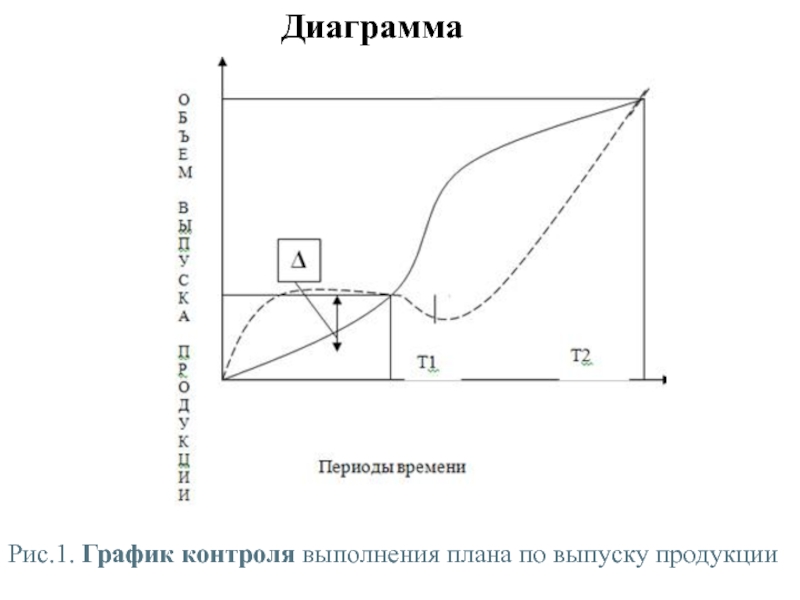
Графики контроля используются в экономическом анализе в процессе рассмотрения выполнения бизнес-планов.
В таком графике (см.рис.1) сплошная линия означает план по выпуску продукции, прерывистая линия — фактическое выполнение плана, Δ — отклонение фактического выполнения от плана.
Слайд 9Диаграмма
Рис.1. График контроля выполнения плана по выпуску продукции
Слайд 10Диаграмма
Линейные диаграммы используются для характеристики вариации, динамики и взаимосвязи.
Линейные диаграммы
для характеристики динамики применяют в следующих случаях:
если
число уровней ряда динамики достаточно велико.;
с целью отображения общей тенденции и характера развития явления;
при необходимости сравнения нескольких динамических рядов;
если нужно сопоставить не абсолютные уровни явления, а темпы роста.
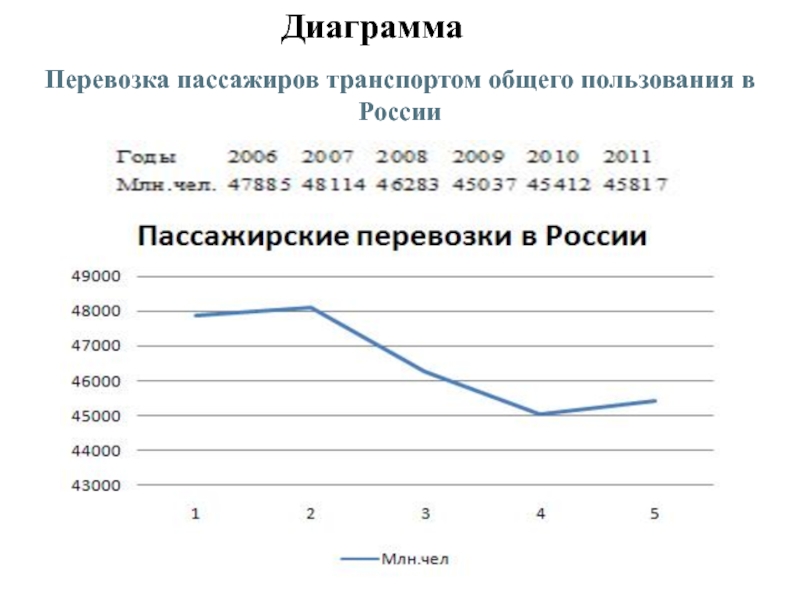
При изображении динамики с помощью линейной диаграммы на ось абсцисс наносят характеристики времени (дни, месяцы, кварталы, годы), а на ось ординат — значения показателя (пассажирские перевозки в России).Построенную диаграмму см.на следующем слайде.
Слайд 11Диаграмма
Перевозка пассажиров транспортом общего пользования в России
Слайд 12Диаграмма
На одном линейном графике можно построить несколько кривых, (см.рис.2), которые
позволят сравнить динамику различных показателей или одного и того же
показателя в разных регионах, отраслях и др.
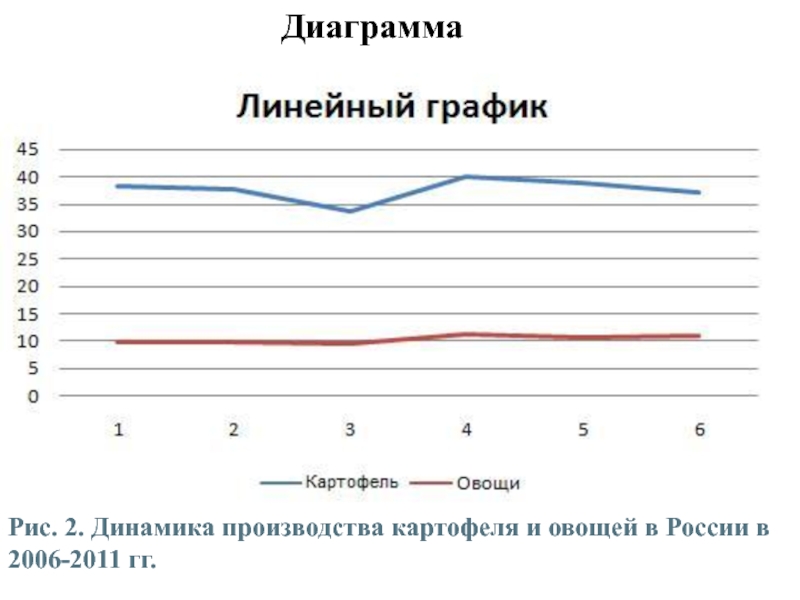
Для построения этого графика воспользуемся данными о динамике производства овощей и картофеля в России.
Производство овощей в России, млн.т.
Слайд 13Диаграмма
Рис. 2. Динамика производства картофеля и овощей в России в
2006-2011 гг.
Слайд 14Диаграмма
Однако линейные диаграммы с равномерной шкалой искажают относительные изменения экономических
показателей. Кроме того, их применение теряет наглядность и даже становится
невозможным при изображении рядов динамики с резко изменяющимися уровнями, что характерно для динамических рядов за длительный период времени. В таких случаях, вместо равномерной шкалы используют полулогарифмическую сетку, в которой на одной оси наносится линейный масштаб, а на другой — логарифмический. В этом случае логарифмический масштаб наносится на ось ординат, а на оси абсцисс располагают равномерную шкалу для отсчета времени по принятым интервалам (год, квартал и пр.). Для построения логарифмической шкалы необходимо: найти логарифмы исходных чисел, начертить ординату и разделить ее на несколько равных частей. Затем нанести на ординату отрезки, пропорциональные абсолютным приростам этих логарифмов, и записать соответствующие логарифмы чисел и их антилогарифмы.
.
Слайд 15Диаграмма
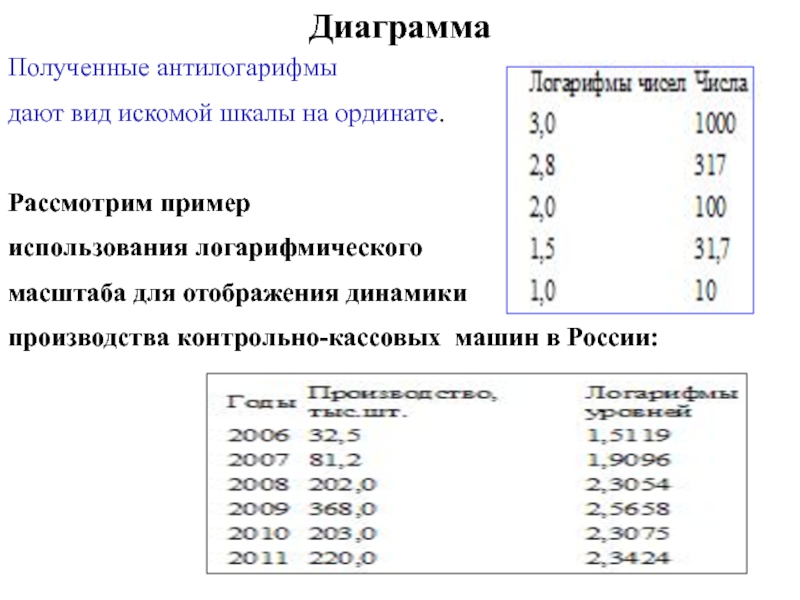
Полученные антилогарифмы
дают вид искомой шкалы на ординате.
Рассмотрим пример
использования
логарифмического
масштаба для отображения динамики
производства контрольно-кассовых машин в России:
Слайд 16Диаграмма
Найдя минимальные и максимальные значения логарифмов производства
контрольно-кассовых машин, строим масштаб с таким расчетом, чтобы все они
разместились на графике.
Затем находим соответствующие точки (с учетом масштаба) и соединяем их прямыми линиями.
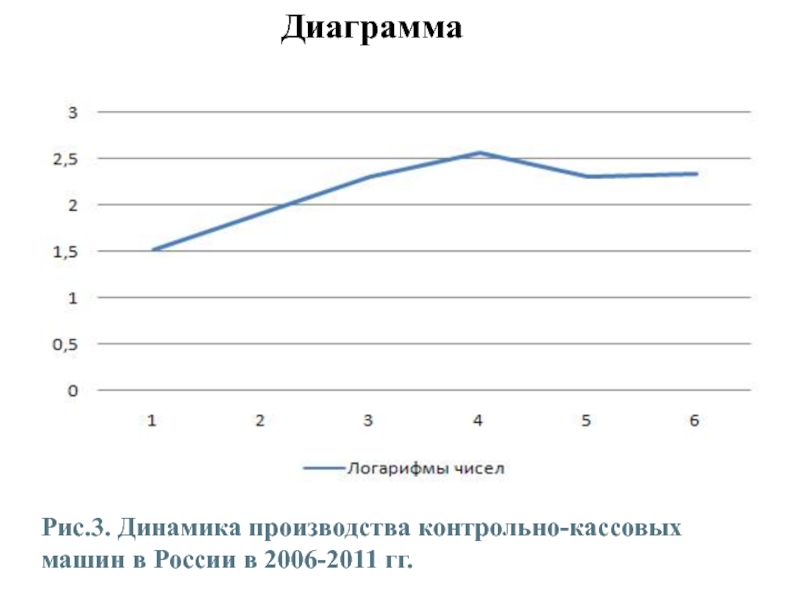
Полученный график (см. рис.3.) с использованием логарифмического масштаба называется диаграммой на полулогарифмической сетке.
Слайд 17Диаграмма
Рис.3. Динамика производства контрольно-кассовых машин в России в 2006-2011 гг.
Слайд 18Диаграмма
Одним из видов линейных диаграмм являются радиальные
диаграммы. Они строятся в полярной системе координат с целью отражения
процессов, ритмически повторяющихся во времени. Радиальные диаграммы можно разделить на два вида: замкнутые и спиральные.
В замкнутых радиальных диаграммах в качестве базы отсчета берется центр круга (рис.4). Вычерчивается круг радиусом, приравненным среднемесячному показателю изучаемого явления, который делится затем на двенадцать равных секторов. Каждый радиус изображает месяц, причем расположение их аналогично циферблату часов. На каждом радиусе делается отметка согласно масштабу, выбранному исходя из данных по каждому месяцу. Если данные превышают среднегодовой уровень, то отметка делается на продолжении радиуса вне окружности. Затем отметки всех месяцев соединяются отрезками.
Слайд 19Диаграмма
Рассмотрим пример построения замкнутой радиальной диаграммы по месячным данным отправления
грузов железнодорожным транспортом общего пользования в России в 1997 г.
Рис.4.
Отправление грузов железнодорожным транспортом общего пользования
В спиральных радиальных диаграммах в качестве базы отсчета берется окружность. При этом декабрь одного года соединяется с январем следующего года, что дает возможность изобразить весь ряд динамики в виде одной кривой. Особенно наглядна такая диаграмма тогда, когда наряду с сезонным ритмом наблюдается неуклонный рост уровней ряда.
Слайд 20Диаграмма
Принцип построения полосовых
диаграмм тот же, что и столбиковых.
Отличие
заключается в том, что
полосовые (или ленточные) графики
представляют значение
показателя не
по вертикальной, а по горизонтальной
оси.
Оба вида диаграмм применяются для
сравнения не только самих величин,
но и их частей. Для изображения
структуры совокупности строят
столбики (полосы) одинакового
размера, принимая целое за 100%,
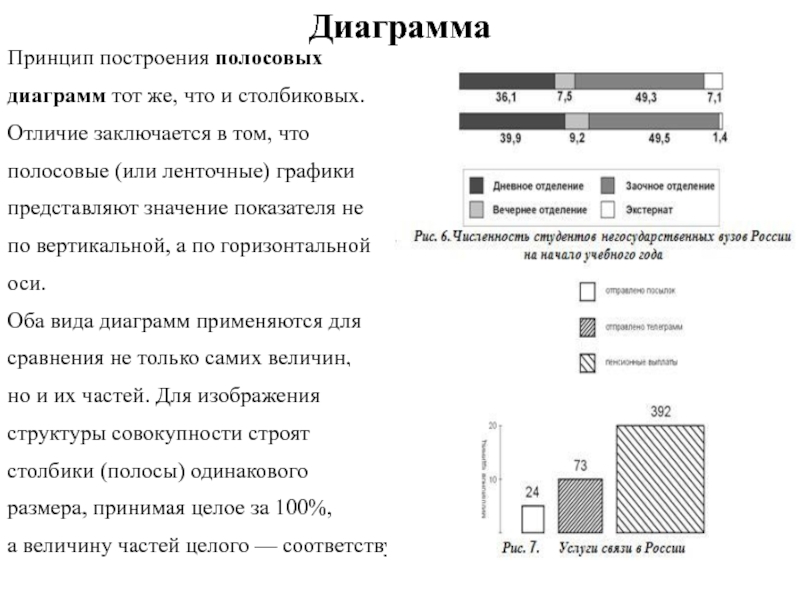
а величину частей целого — соответствующей удельным весам (рис. 6,7).
Слайд 21Диаграмма
Для изображения показателей с противоположным содержанием (импорт и экспорт, сальдо
положительное и отрицательное, возрастная пирамида) строят разнонаправленные столбиковые или полосовые
диаграммы.
Основу квадратных, треугольных и круговых диаграмм составляет изображение значения показателя величиной площади геометрической фигуры.
Квадратная диаграмма
Для построения квадратной диаграммы устанавливают размер стороны квадрата путем извлечения корня квадратного из значения показателя.
Так, например, для построения диаграммы на рис. 7 из объема услуг связи за 1997 г. в России по отправлению телеграмм
(73 млн.), пенсионных выплат (392 млн.), посылок (24 млн.) квадратные корни составили соответственно 8,5; 19,8; 4,9.
Слайд 22Диаграмма
Круговая диаграмма
Круговые диаграммы строятся в виде площади кругов, радиусы которых
равны корню квадратному из значений показателя.
Секторная диаграмма
Для изображения структуры (состава)
совокупности используются секторные диаграммы. Круговая секторная диаграмма строится путем разделения круга на секторы пропорционально удельному весу частей в целом. Размер каждого сектора определяется величиной угла расчета (1% соответствует 3,60).
Пример. Доля продовольственных товаров в объеме розничного товарооборота России составила в 1992 г. 55%, а в 1997 г. — 49%, доля непродовольственных товаров составила соответственно 45% и 51%.
Слайд 23Диаграмма
Построим два круга одинакового радиуса, а для изображения секторов определим
центральные углы: для продовольственных товаров 3,60*55 = 1980, 3,6*49 =
176,40; для непродовольственных товаров 3,60*45 = 1620; 3,60*51 = 183,60. Разделим круги на соответствующие секторы (рис.8).
Слайд 24Диаграмма
Разновидностью диаграмм, представляющих структуру (кроме столбиковых и полосовых), является диаграмма
треугольная.
Она применяется для одновременного изображения трех величин, изображающих элементы
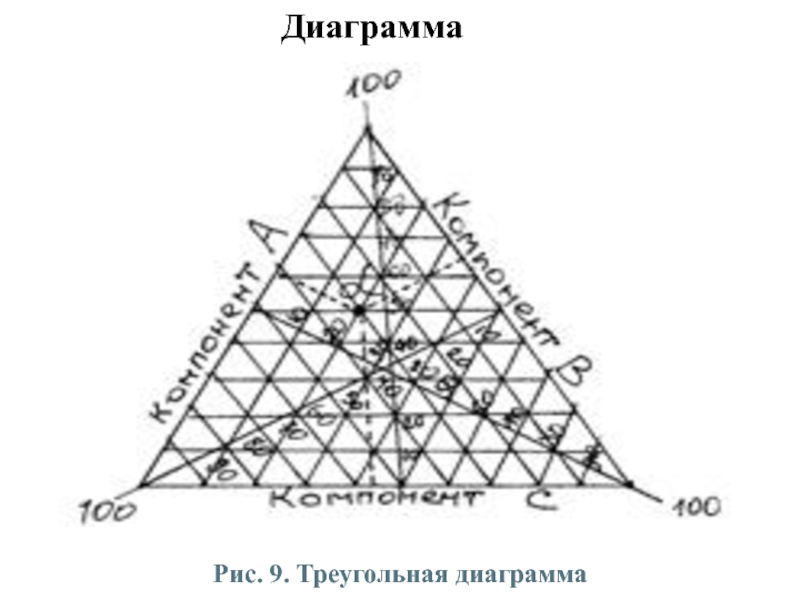
или составные части целого. Треугольная диаграмма представляет собой равносторонний треугольник, каждая сторона которого является равномерной масштабной шкалой от 0 до 100.
Внутри строится координатная сетка, соответствующая линиям, проводимым параллельно сторонам треугольника.
Перпендикуляры из любой точки координатной сетки представляют доли трех компонентов, соответствует в сумме 100% (рис.9). Точка на графике соответствует 20% (по А), 30% (по В) и 50% (по С).
Слайд 25Диаграмма
Рис. 9. Треугольная диаграмма