Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Л_28_Числовые_ряды.ppt
Содержание
- 1. Л_28_Числовые_ряды.ppt
- 2. 1. Основные определения
- 3. Числовым рядом
- 4. Суммы n = 1, 2, … называются
- 5. Сумма сходящегося ряда – предел последовательности его
- 6. 2. Свойства рядов
- 7. 1.Сходимость или расходимость ряда не нарушится если изменить, отбросить или добавить конечное число членов ряда.
- 8. 2.Рассмотрим два ряда и где С –
- 9. 3.Рассмотрим два ряда и Суммой или разностью
- 10. 3.Теорема. Если ряды и сходятся и
- 11. 3.Разность двух сходящихся рядов также будет сходящимся
- 12. Исследование рядовИсследование на сходимость Нахождение суммы ряда
- 13. Пример:Исследовать сходимость бесконечной геометрической прогрессии где (*)
- 14. Пример:Sn – сумма n первых членов ГП:
- 15. Пример:1)
- 16. Пример:2)Вывод:ряд (*) расходится и суммы не имеет
- 17. Пример:3)Вывод:ряд (*) расходится и суммы не имеет
- 18. Пример:4)n четно:n нечетно:Вывод:ряд (*) расходитсяSn не стремится ни к какому пределу
- 19. 3. Признаки сходимости
- 20. Критерий Коши (необходимые и достаточные условия сходимости
- 21. был сходящемся, необходимо и достаточно, чтобы для
- 22. 1. Необходимое условие сходимости1) Если
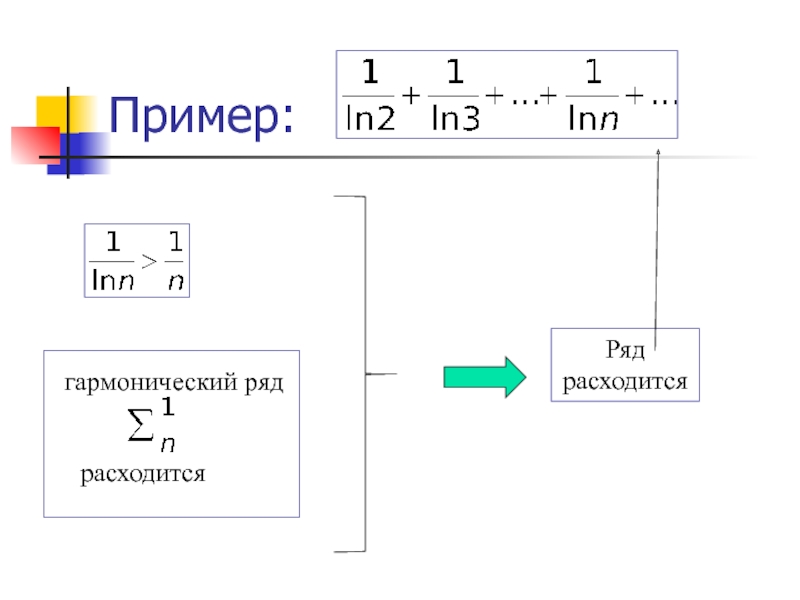
- 23. Пример:Гармонический ряд является расходящимся, хотя его общий член и стремится к нулю.
- 24. Пример:Исследовать сходимость ряда Найдем Необходимый признак сходимости не выполняется, значит ряд расходится.
- 25. 2. Необходимое условие сходимости1) Если
- 26. Пример:Ряд 1-1+1-1+1-1+ … +(-1)n+1+… расходится, т.к.
- 27. 4. Знакопостоянные ряды
- 28. При изучении знакопостоянных рядов ограничимся рассмотрением рядов
- 29. Для сходимости ряда со знакопостоянными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены.Теорема
- 30. Признак сравнения рядов с неотрицательными членами .
- 31. Пример:Ряд расходится
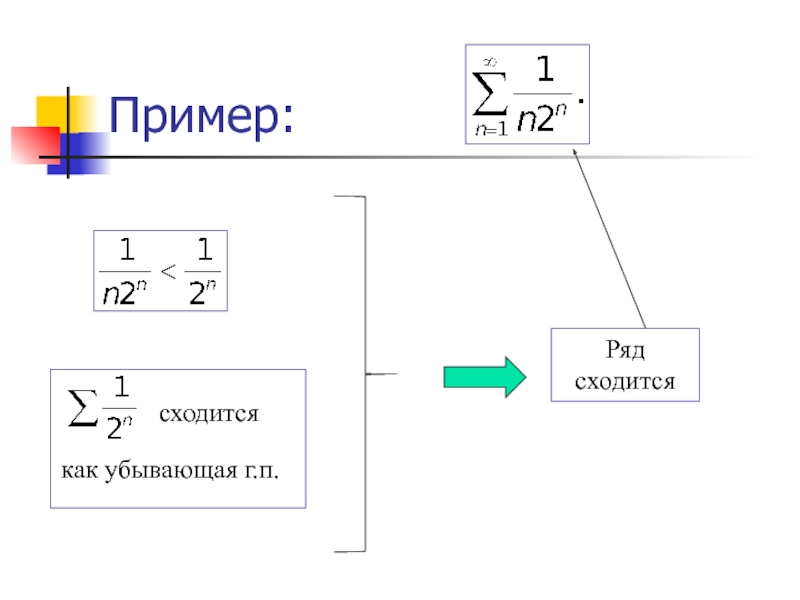
- 32. Пример:Ряд сходится
- 33. Признак сходимости Теорема.Если и существует предел где
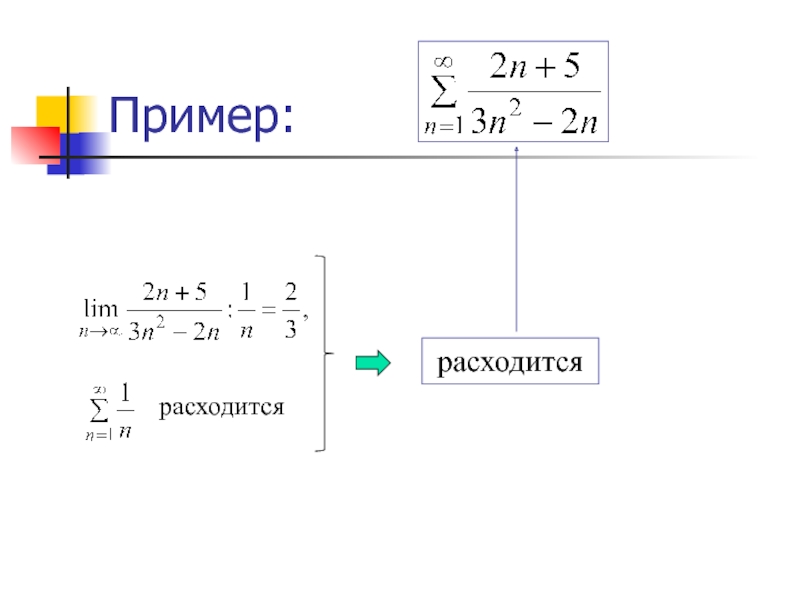
- 34. Пример: расходится расходится
- 35. Предельный признак Даламбера Жан Лерон Даламбер (1717
- 36. Пример:Ряд сходится
- 37. Пример:Ряд сходится
- 38. Признак Коши (радикальный)Коши Огюстен Луи (21.08.1789
- 39. Пример: Ряд сходится
- 40. Пример:?ряд расходится
- 41. Признак Коши (интегральный)Коши Огюстен Луи (21.08.1789
- 42. Пример:(ряд Дирехле или общегармонический ряд) удовлетворяет условиям интегрального признака Коши
- 43. Пример:(ряд Дирехле или общегармонический ряд) сходится при р>1; расходится р ≤1.
- 44. 5. Знакопеременные ряды
- 45. 5.1 Знакочередующиеся ряды где
- 46. Признак Лейбница Лейбниц, Готфрид Вильгельм (1.07.1646 –
- 47. Пример:Ряд сходится
- 48. Теорема(1)(2)Из сходимости ряда (2) следует сходимость ряда (1).
- 49. называется абсолютно сходящимся, если сходится ряд
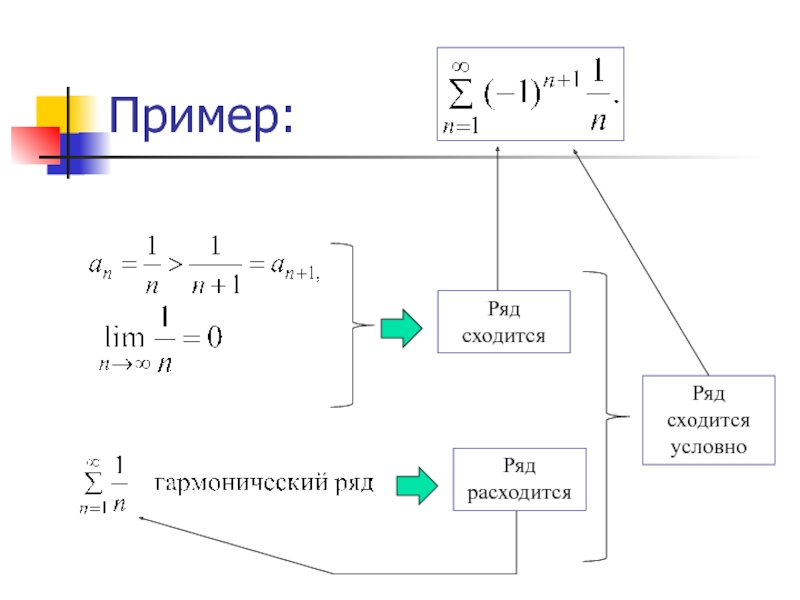
- 50. Пример:Ряд сходитсяРяд расходитсяРяд сходится условно
- 51. Свойства абсолютно сходящихся рядов Если ряд абсолютно
- 52. Свойства абсолютно сходящихся рядов Под произведением двух
- 53. ЗамечаниеВ случае условно сходящихся рядов соответствующие свойства, вообще говоря, не имеют места.
- 54. Пример:Условно сходитсяS =Сумма уменьшилась вдвое!!!!!!!
- 55. Замечание:Для установления абсолютной сходимости используют все признаки
- 56. Признак Даламбера Жан Лерон Даламбер (1717 –
- 57. Признак КошиКоши Огюстен Луи (21.08.1789 -
- 58. Спасибо за внимание!
- 59. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Числовые ряды
1. Основные определения.
2. Свойства рядов.
3. Признаки сходимости.
4. Знакопостоянные
ряды.
Слайд 4Суммы
n = 1, 2, … называются частными (частичными) суммами
ряда.
называется сходящимся, если сходится последовательность его частных сумм.
Слайд 5
Сумма сходящегося ряда – предел последовательности его частных сумм:
Если последовательность
частных сумм ряда расходится, т.е. не имеет предела, или имеет
бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммыСлайд 71.
Сходимость или расходимость ряда не нарушится если изменить, отбросить или
добавить конечное число членов ряда.
Слайд 82.
Рассмотрим два ряда
и
где С – постоянное число.
Теорема.
Если ряд
сходится и его сумма равна S, то
ряд тоже сходится, и его сумма равна СS. (C ≠ 0)
Слайд 93.
Рассмотрим два ряда
и
Суммой или разностью этих рядов
будет называться ряд
где элементы получены в результате сложения (вычитания)
исходных элементов с одинаковыми номерами.Слайд 103.
Теорема. Если ряды
и
сходятся и их суммы равны
соответственно S и σ, то ряд
тоже сходится и
его сумма равна S + σ.
Слайд 113.
Разность двух сходящихся рядов также будет сходящимся рядом.
Сумма сходящегося и
расходящегося рядов будет расходящимся рядом.
О сумме двух расходящихся рядов общего
утверждения сделать нельзя.Слайд 20Критерий Коши (необходимые и достаточные условия сходимости ряда)
Для того, чтобы
последовательность
была сходящейся, необходимо и достаточно, чтобы для любого
существовал
такой номер N, что при n > N и любом p > 0,
где р – целое число, выполнялось бы неравенство:Слайд 21был сходящемся, необходимо и достаточно, чтобы для любого
Критерий Коши
(необходимые и достаточные условия сходимости ряда)
Для того, чтобы ряд
существовал
такой номер N, что при n > N и любом p > 0,
где р – целое число, выполнялось бы неравенство:
Слайд 22
1. Необходимое условие сходимости
1) Если ряд
сходится, то необходимо, чтобы
общий член un стремился к нулю.
Общий член не стремится
к нулюряд расходится
Общий член стремится к нулю
ряд
сходится
?
Слайд 24Пример:
Исследовать сходимость ряда
Найдем
Необходимый признак сходимости не выполняется, значит
ряд расходится.
Слайд 25
2. Необходимое условие сходимости
1) Если ряд
сходится, то последовательность его
частных сумм ограничена.
Последовательность частных сумм не ограничена
ряд расходится
Последовательность
частных сумм ограниченаряд
сходится
?
Слайд 26Пример:
Ряд 1-1+1-1+1-1+ … +(-1)n+1+… расходится,
т.к. расходится последовательность его частных
сумм в силу того, что
Однако, при этом последовательность частных сумм
ограничена, т.к. при любом n.
Слайд 28
При изучении знакопостоянных рядов ограничимся рассмотрением рядов с неотрицательными членами,
т.к. при умножении на –1 из этих рядов можно получить
ряды с отрицательными членамиСлайд 29Для сходимости ряда
со знакопостоянными членами необходимо и достаточно, чтобы
частные суммы ряда были ограничены.
Теорема
Слайд 33Признак сходимости
Теорема.
Если
и существует предел
где h –
число, отличное от нуля, то ряды
и
ведут одинаково в
смысле сходимости.Слайд 35Предельный признак Даламбера
Жан Лерон Даламбер (1717 – 1783) –
французский математик
Если существует предел
то при ρ < 1
ряд сходится, а при ρ > 1 – расходится. Если ρ = 1, то на вопрос о сходимости ответить нельзя.
Слайд 38Признак Коши (радикальный)
Коши Огюстен Луи
(21.08.1789 - 23.05.1857) –
французский математик
Если
существует предел
то при ρ < 1 ряд сходится,
а
при ρ > 1 – расходится. Если ρ = 1, то на вопрос о сходимости ответить нельзя.
Слайд 41Признак Коши (интегральный)
Коши Огюстен Луи
(21.08.1789 - 23.05.1857) –
французский математик
Если
ϕ (х) – непрерывная положительная функция, убывающая на промежутке [1;∞),
то ряд и несобственный интеграл
одинаковы в смысле сходимости.
Слайд 42Пример:
(ряд Дирехле или общегармонический ряд)
удовлетворяет условиям интегрального признака
Коши
Слайд 46Признак Лейбница
Лейбниц, Готфрид Вильгельм (1.07.1646 – 14.11.1716) – немецкий
математик
Если у знакочередующегося ряда
и общий член стремится к
нулю то ряд сходится.
абсолютные величины ui убывают
При этом сумма ряда удовлетворяет неравенству:
Слайд 49называется абсолютно сходящимся,
если сходится ряд
Определения:
Ряд
Ряд
называется условно
сходящимся,
если он сходится, а ряд
расходится.
Слайд 51Свойства абсолютно сходящихся рядов
Если ряд абсолютно сходится и имеет
сумму S, то ряд, полученный из него престановкой членов, также
сходится и имеет ту же сумму S, что и исходный ряд (теорема Дирихле).Абсолютно сходящиеся ряды с суммами S1 и S2 можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна S1+S2 (или соответственно S1-S2).
Слайд 52Свойства абсолютно сходящихся рядов
Под произведением двух рядов
и
понимают ряд вида
Произведение двух сходящихся рядов с суммами
S1 и S2 есть абсолютно сходящийся ряд, сумма которого равна Слайд 53Замечание
В случае условно сходящихся рядов соответствующие свойства, вообще говоря, не
имеют места.
Слайд 55Замечание:
Для установления абсолютной сходимости используют все признаки сходимости знакоположительных рядов,
заменяя всюду общий член ряда его модулем.
Слайд 56Признак Даламбера
Жан Лерон Даламбер (1717 – 1783) – французский
математик
Если существует предел
то
при ρ < 1 ряд сходится
абсолютно, а при ρ > 1 – расходится. Если ρ = 1, то на вопрос о сходимости ответить нельзя.
Слайд 57Признак Коши
Коши Огюстен Луи
(21.08.1789 - 23.05.1857) –
французский математик
Если существует
предел
то
при ρ < 1 ряд сходится абсолютно,
при
ρ > 1 – расходится.
Если ρ = 1, то на вопрос о сходимости ответить нельзя.