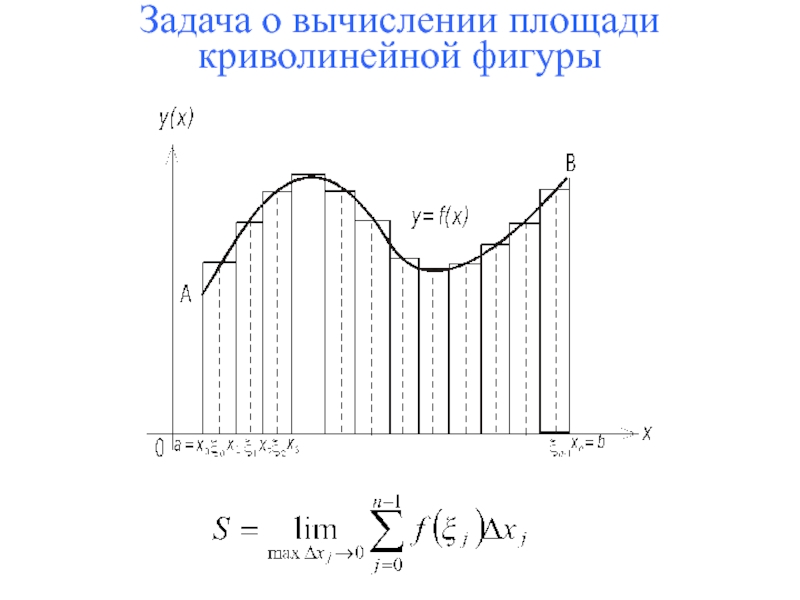
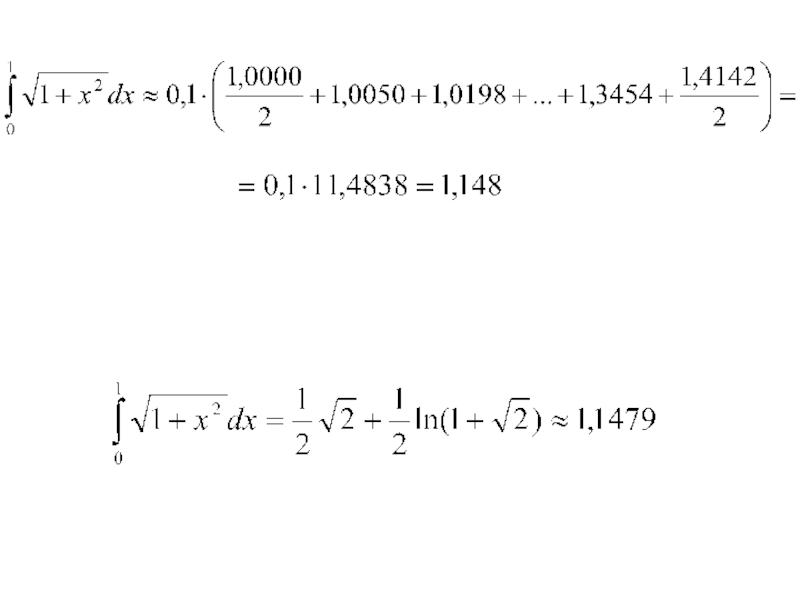о нахождении пройденного пути точки по заданной скорости .
3.
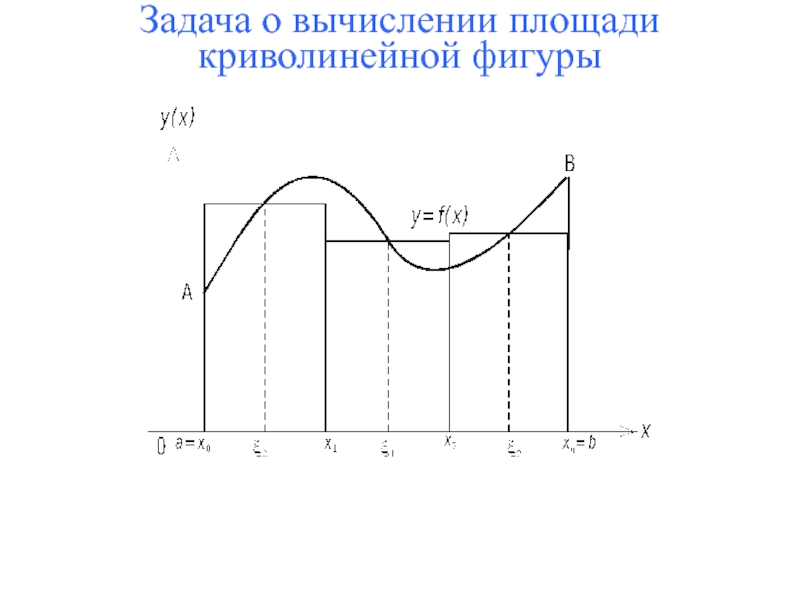
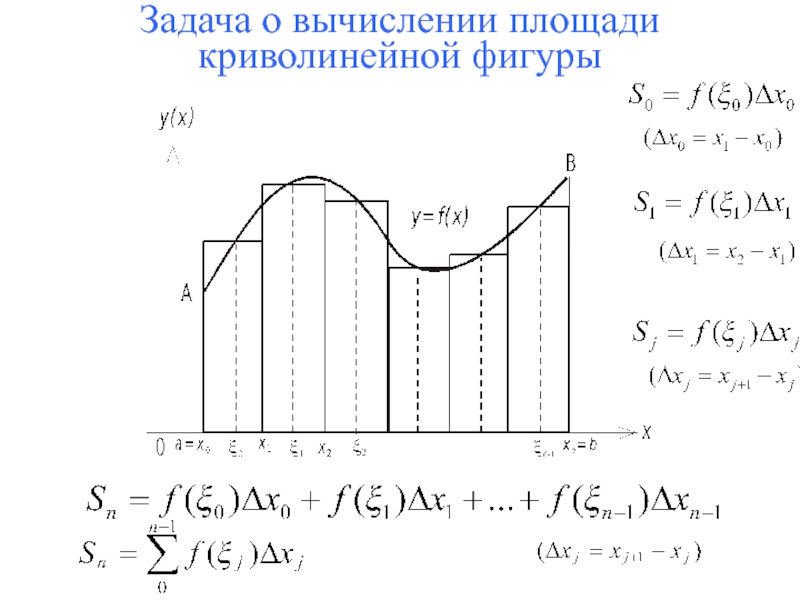
Общее понятие определенного интеграла.4. Свойства определенных интегралов.
5. Правила интегрирования.
6. Несобственные интегралы.
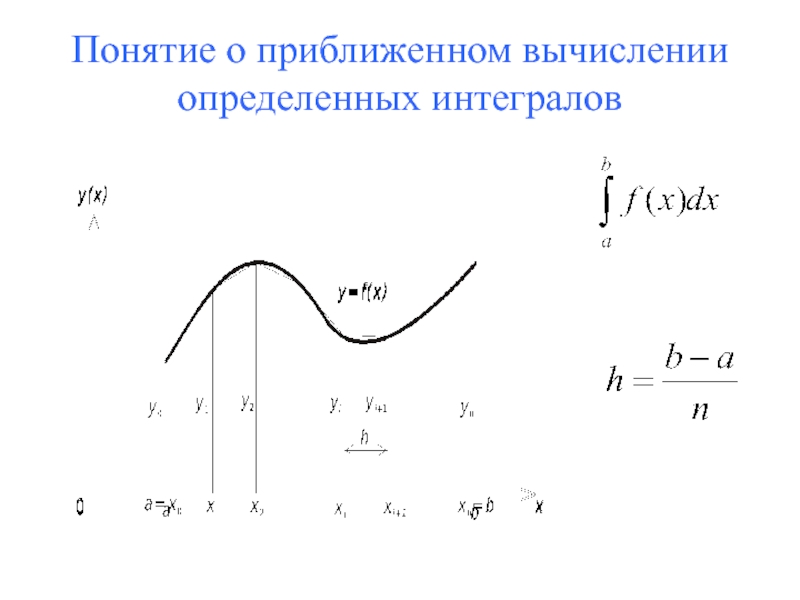
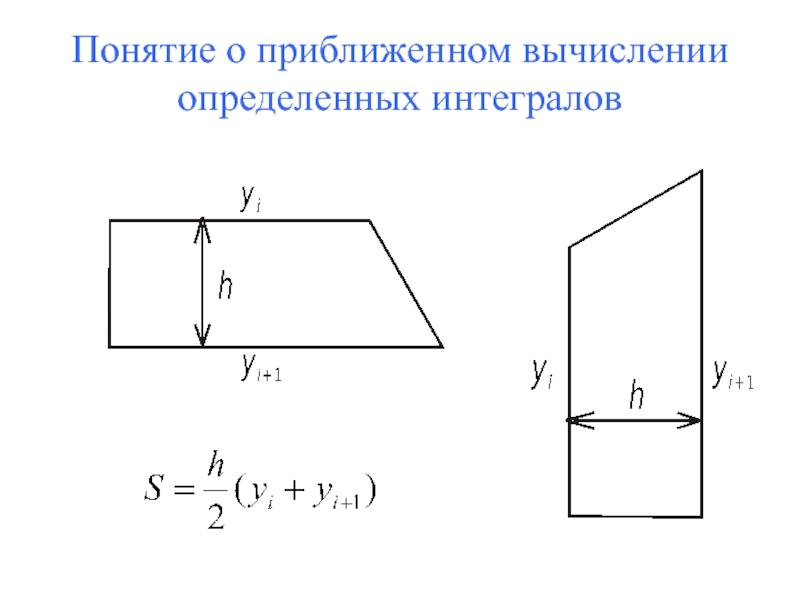
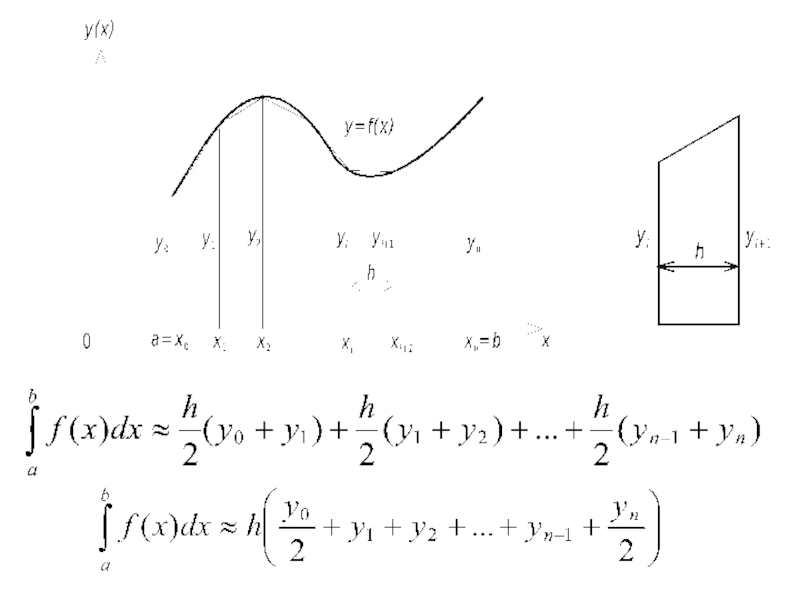
7. Понятие о приближенном вычислении определенных интегралов
















![Л_21_Определенный_интеграл.ppt Свойства определенных интегралов [A F(x)]′ =Af(x) 5. Свойства определенных интегралов [A F(x)]′ =Af(x) 5.](/img/thumbs/3ffd87f2ae27e51f4fbca87751f4d170-800x.jpg)




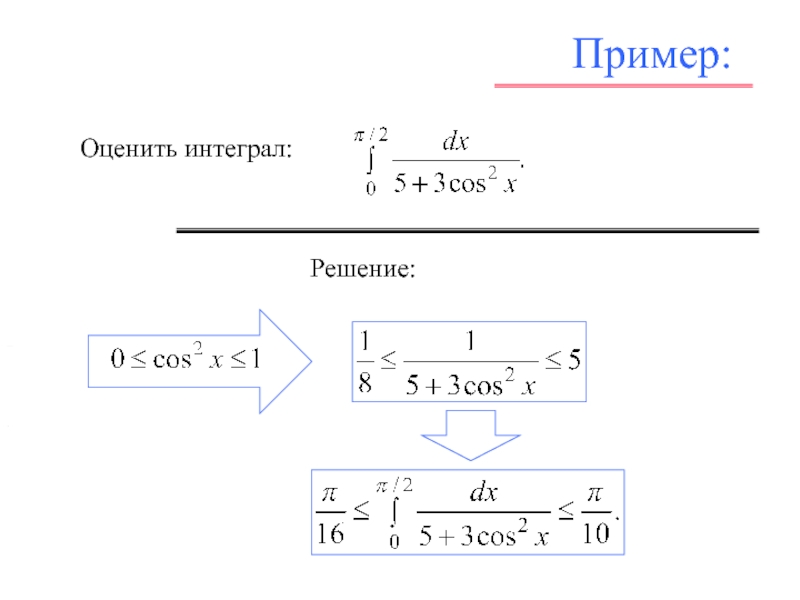
![Л_21_Определенный_интеграл.ppt Свойства определенных интегралов 7. Оценка определенного интеграла.Если на [a, b], то Свойства определенных интегралов 7. Оценка определенного интеграла.Если на [a, b], то](/img/thumbs/3d4138e7c854ab4dc8479197f5b616ba-800x.jpg)

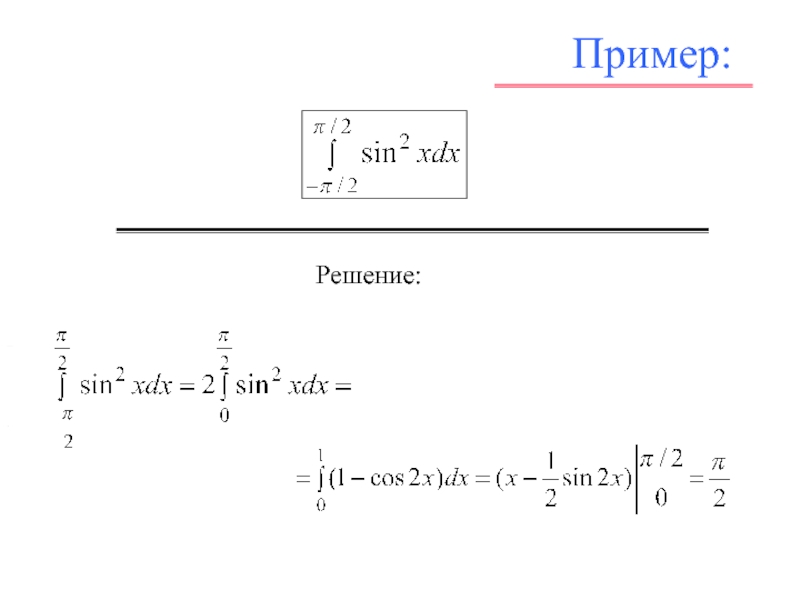
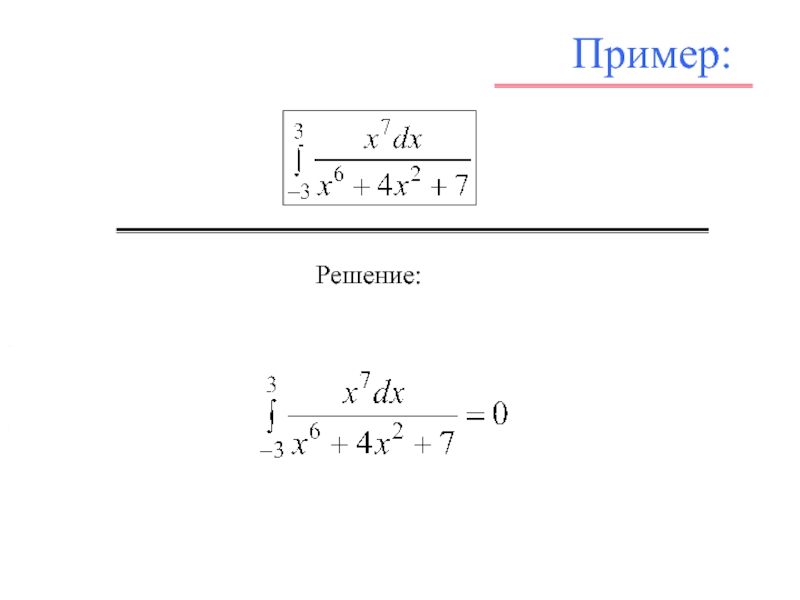

![Л_21_Определенный_интеграл.ppt Пример: Решение: Найти среднее значение функции на промежутке [0, 2π]. Пример: Решение: Найти среднее значение функции на промежутке [0, 2π].](/img/thumbs/93477fe58ba783b655defcc08084a21b-800x.jpg)




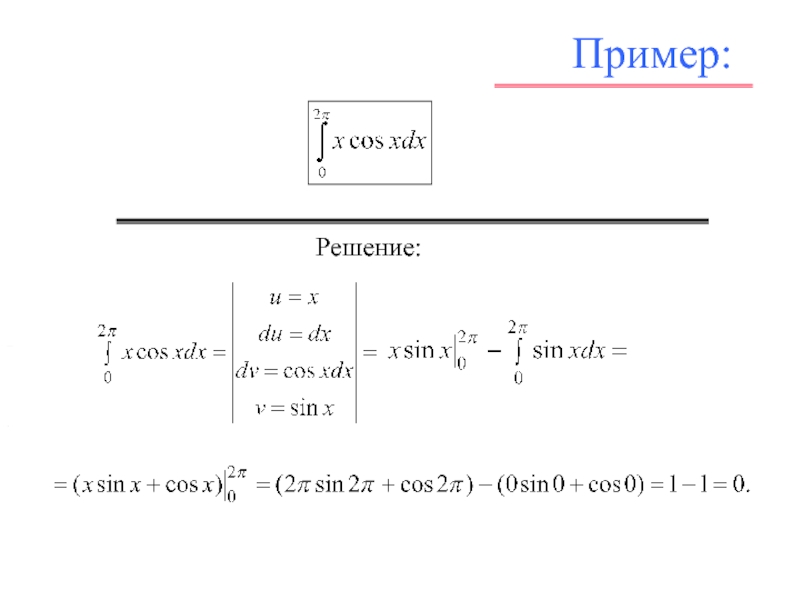
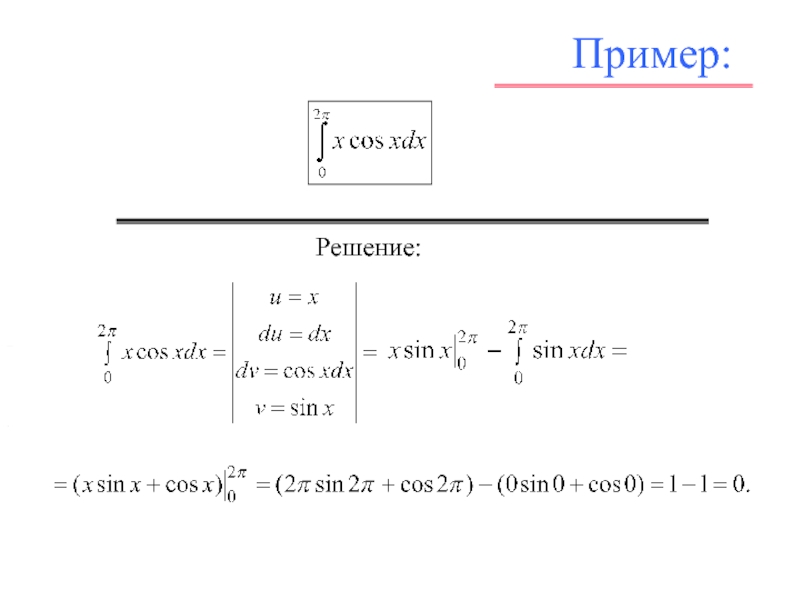
![Л_21_Определенный_интеграл.ppt Интегрирование по частям где u = u(x), v = v(x) – непрерывно дифференцируемые функции на отрезке [α, β]. Интегрирование по частям где u = u(x), v = v(x) – непрерывно дифференцируемые функции на отрезке [α, β].](/img/thumbs/c218e0fa259899736489d2834e819c01-800x.jpg)

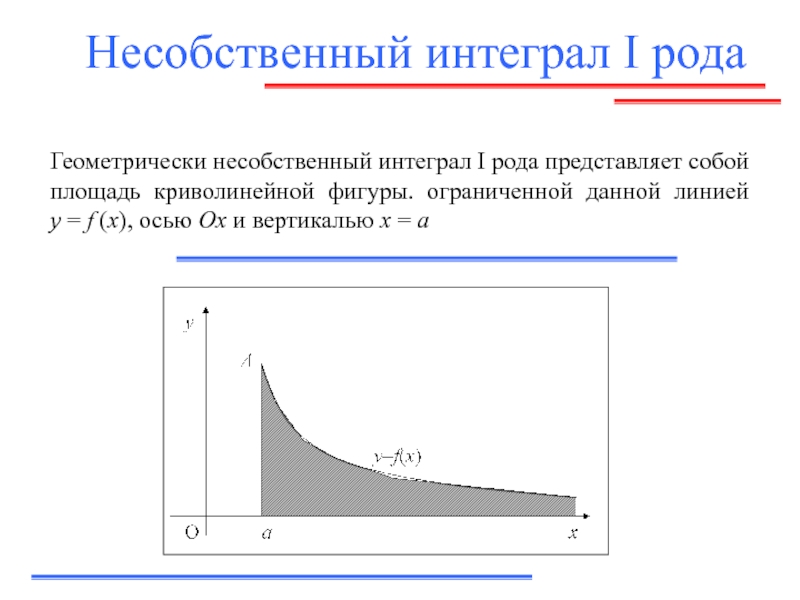
![Л_21_Определенный_интеграл.ppt предполагалось: При определении интеграла1) промежуток интегрирования [a, b] конечен и 2) подынтегральная функция предполагалось: При определении интеграла1) промежуток интегрирования [a, b] конечен и 2) подынтегральная функция f (x) непрерывна на отрезке [a, b].](/img/thumbs/3a5a8f1a71b44ae106ca57bec4472833-800x.jpg)
![Л_21_Определенный_интеграл.ppt предполагалось: При определении интеграла1) промежуток интегрирования [a, b] конечен и 2) подынтегральная функция предполагалось: При определении интеграла1) промежуток интегрирования [a, b] конечен и 2) подынтегральная функция f (x) непрерывна на отрезке [a, b].](/img/thumbs/ff19b741b848fa08d46b5b9552d8d39d-800x.jpg)
![Л_21_Определенный_интеграл.ppt 1) промежуток интегрирования [a, b] конечен и 2) подынтегральная функция f (x) непрерывна на 1) промежуток интегрирования [a, b] конечен и 2) подынтегральная функция f (x) непрерывна на отрезке [a, b]. ? Такой определенный интеграл](/img/thumbs/a326e583dd22344ca8f0dcc663405fa8-800x.jpg)
![Л_21_Определенный_интеграл.ppt 1) промежуток интегрирования [a, b] конечен и 2) подынтегральная функция f (x) непрерывна на 1) промежуток интегрирования [a, b] конечен и 2) подынтегральная функция f (x) непрерывна на отрезке [a, b]. ? Если нарушается, по](/img/thumbs/d987cfdfa2fd2e40d560792e699957e1-800x.jpg)






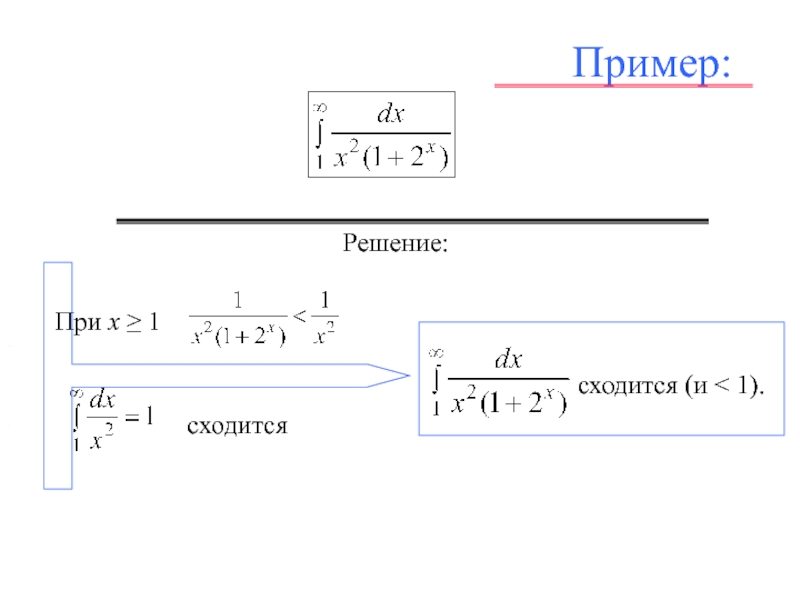

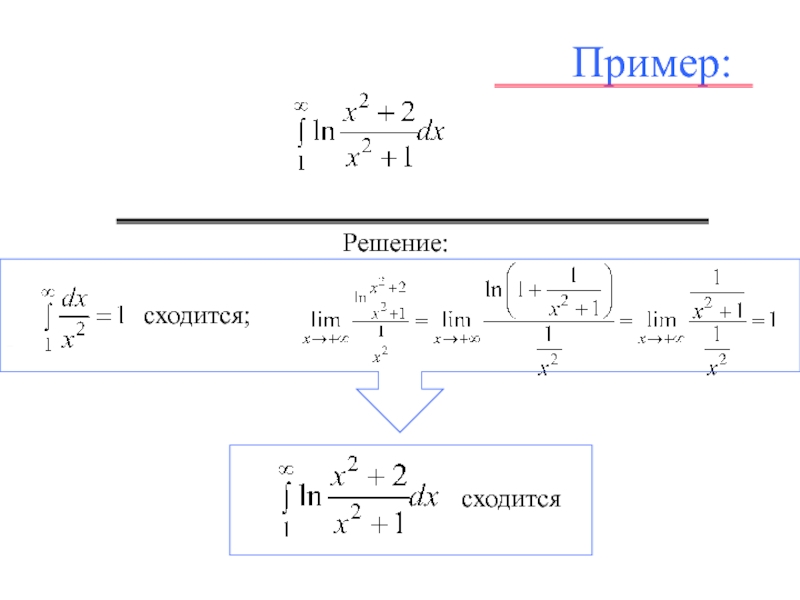

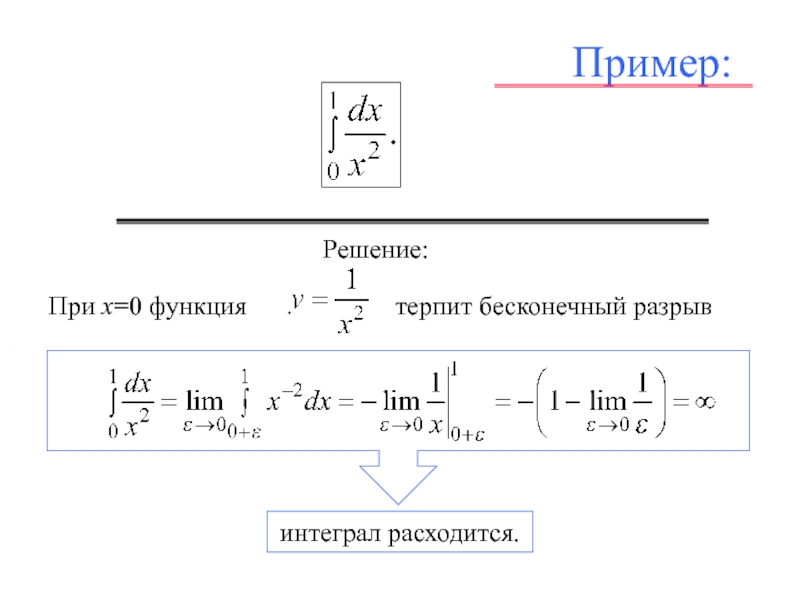
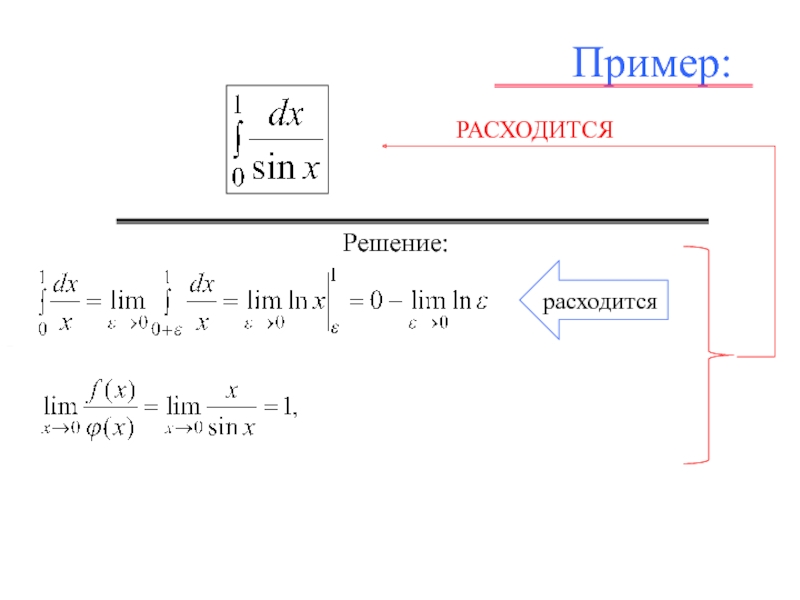
![Л_21_Определенный_интеграл.ppt Если функция f (x) имеет бесконечный разрыв в точке с отрезка [a, b] и непрерывна при a ≤ x Если функция f (x) имеет бесконечный разрыв в точке с отрезка [a, b] и непрерывна при a ≤ x](/img/thumbs/5c23a1511a176a60731b2bb597900268-800x.jpg)