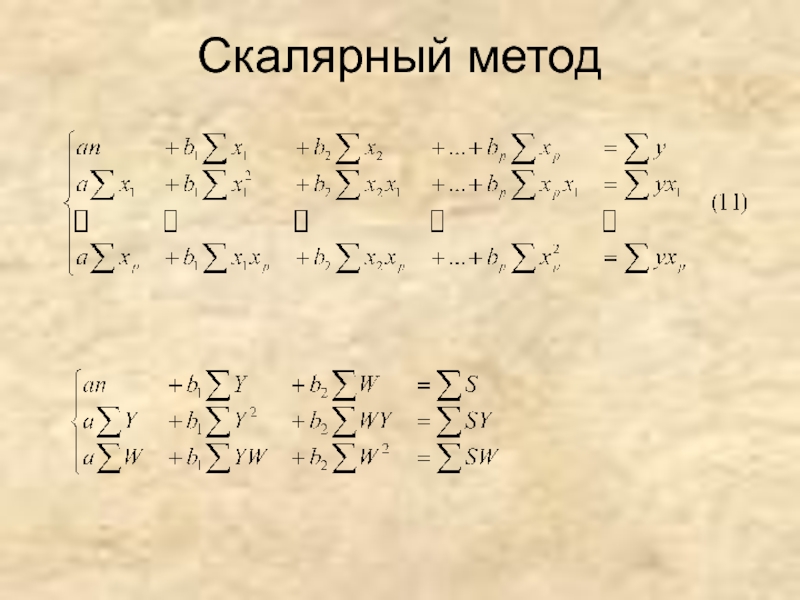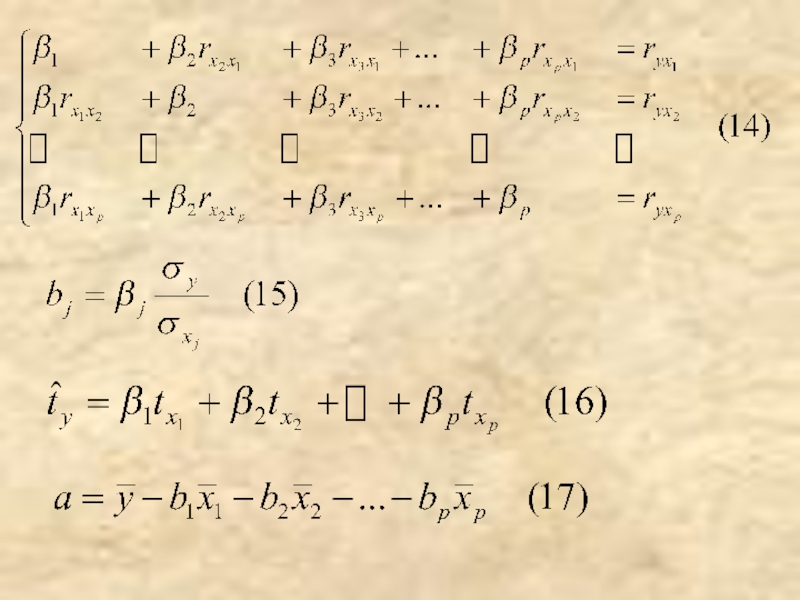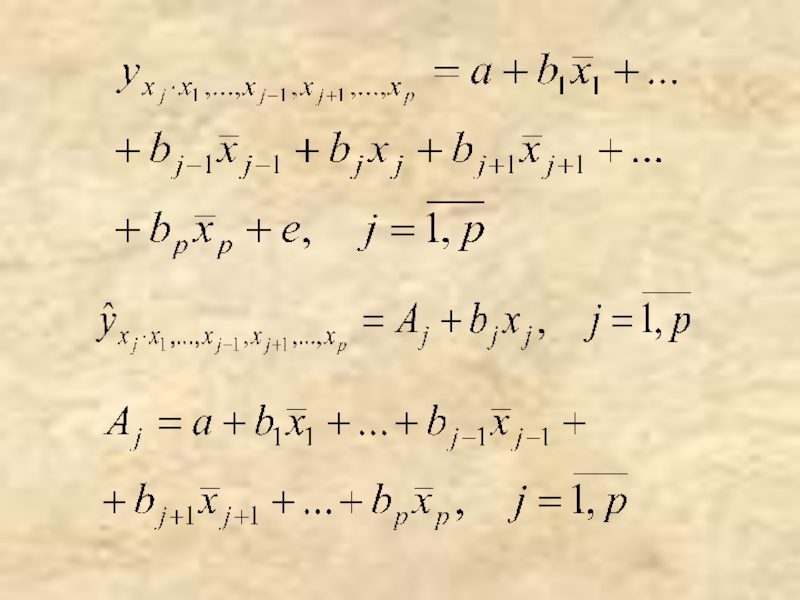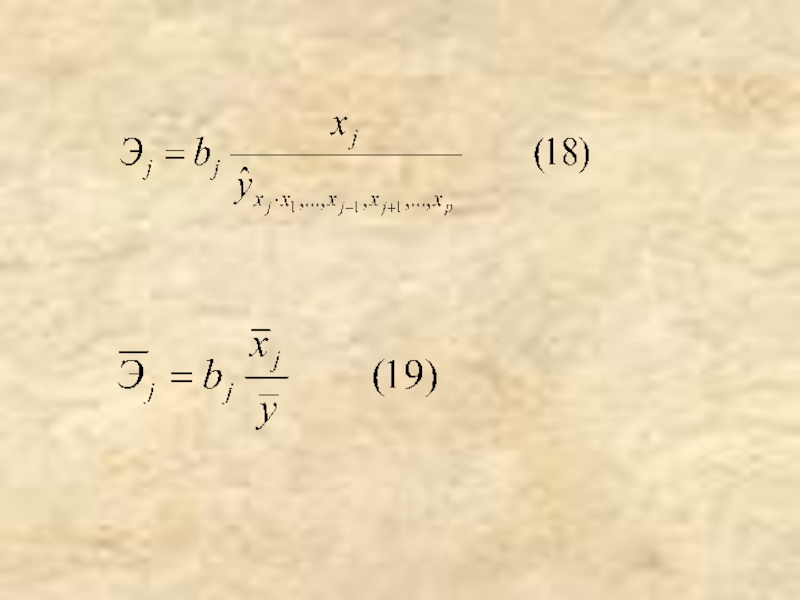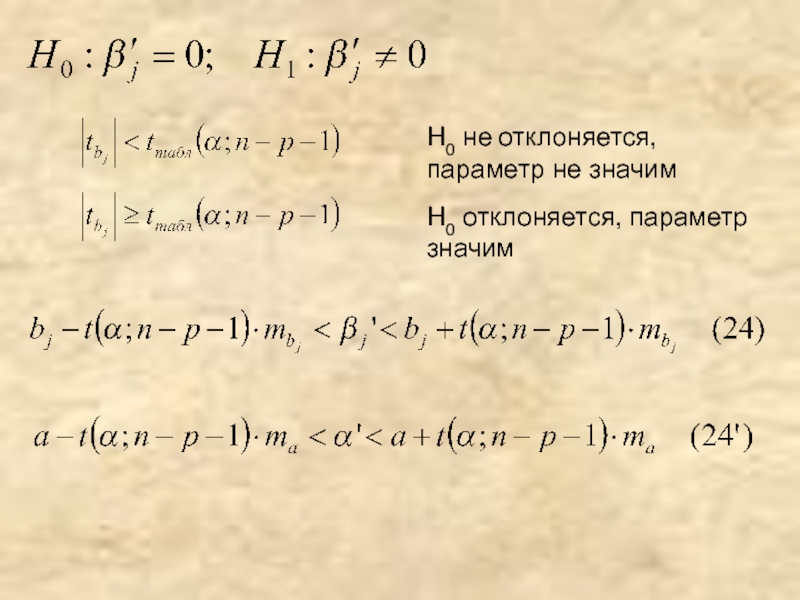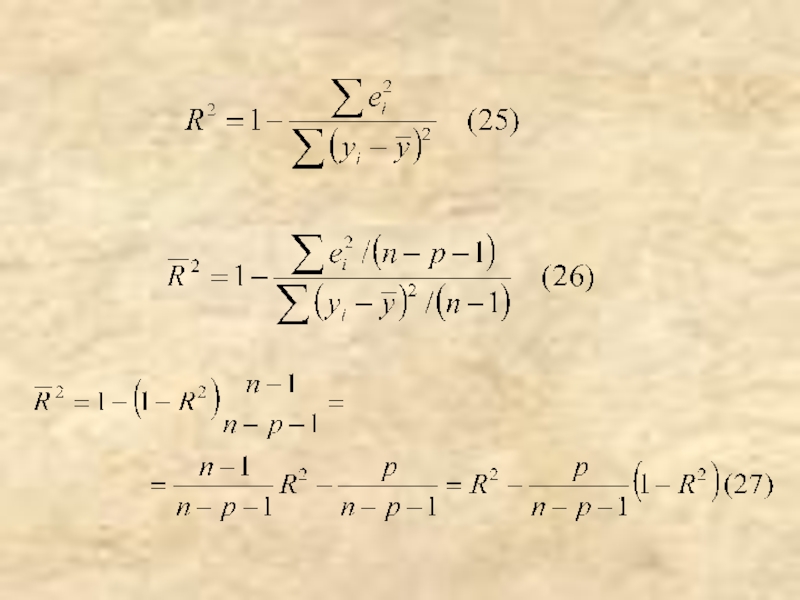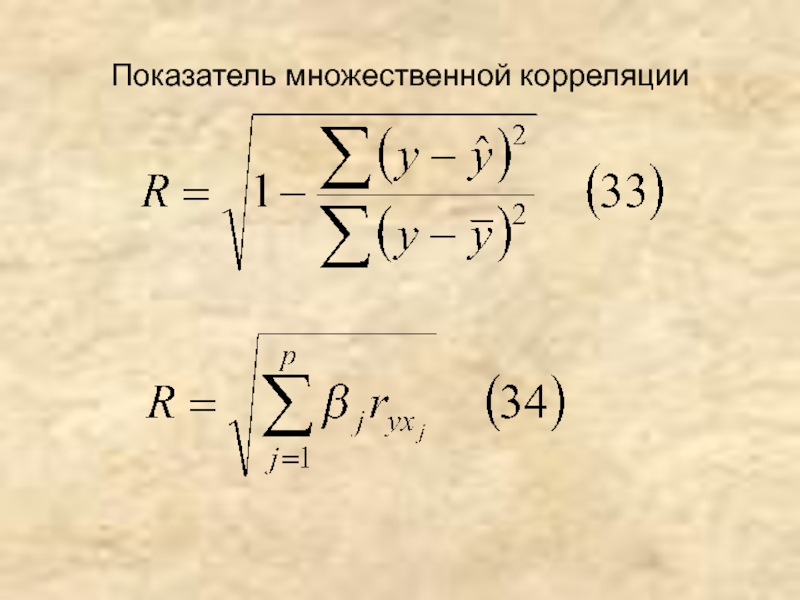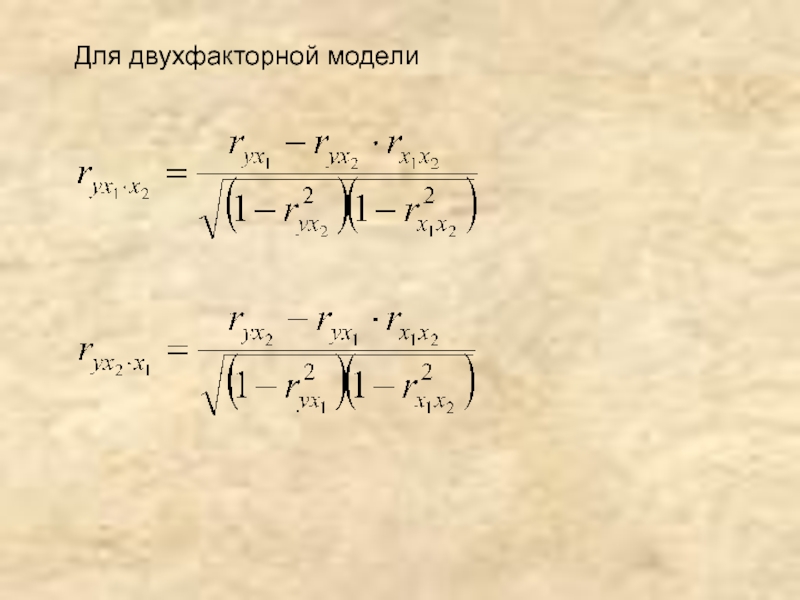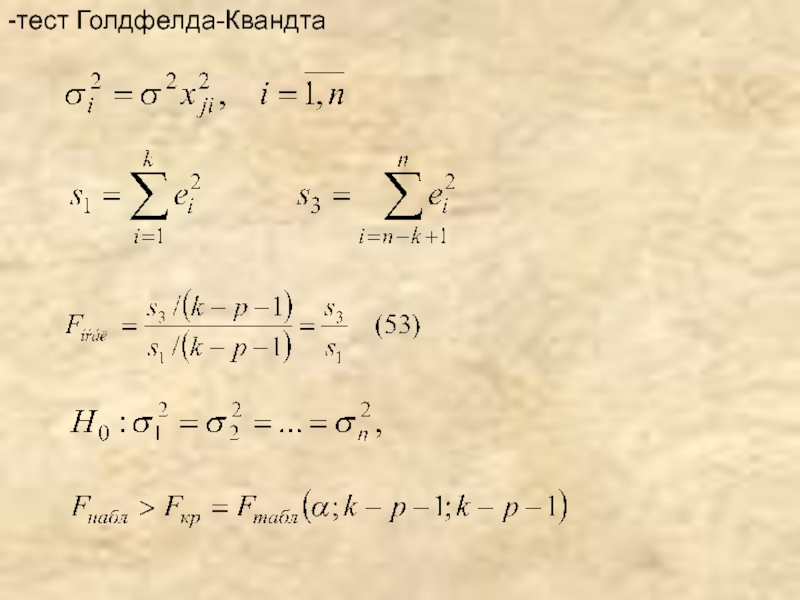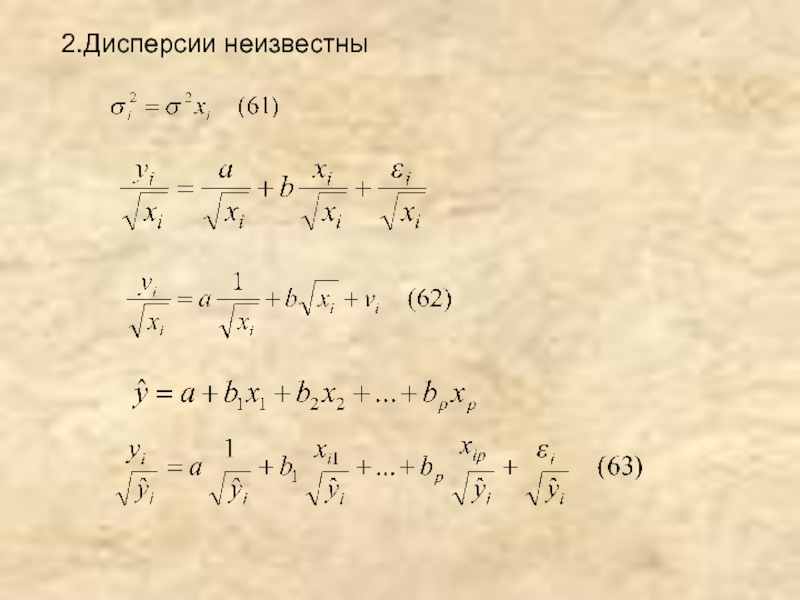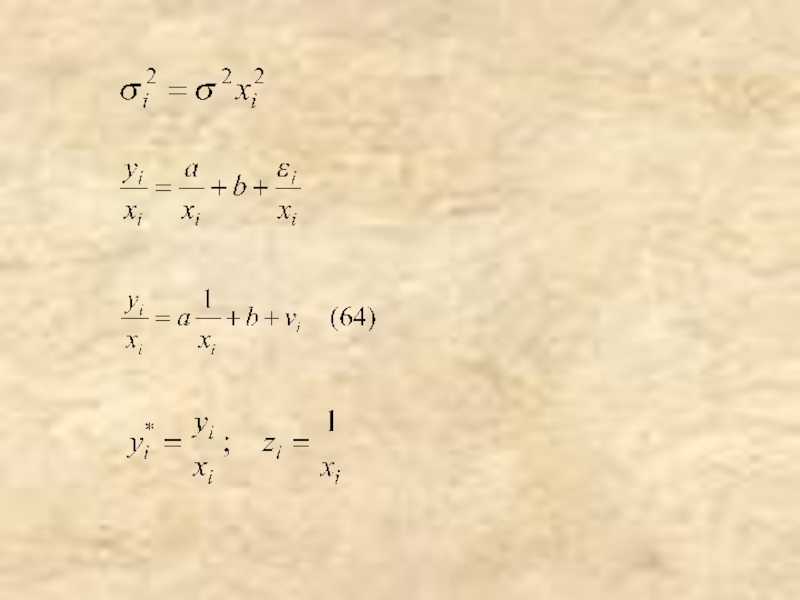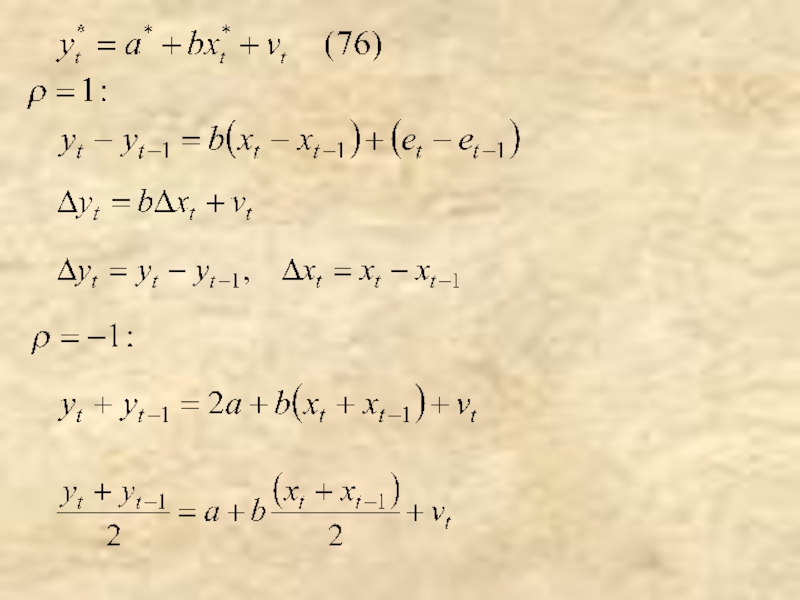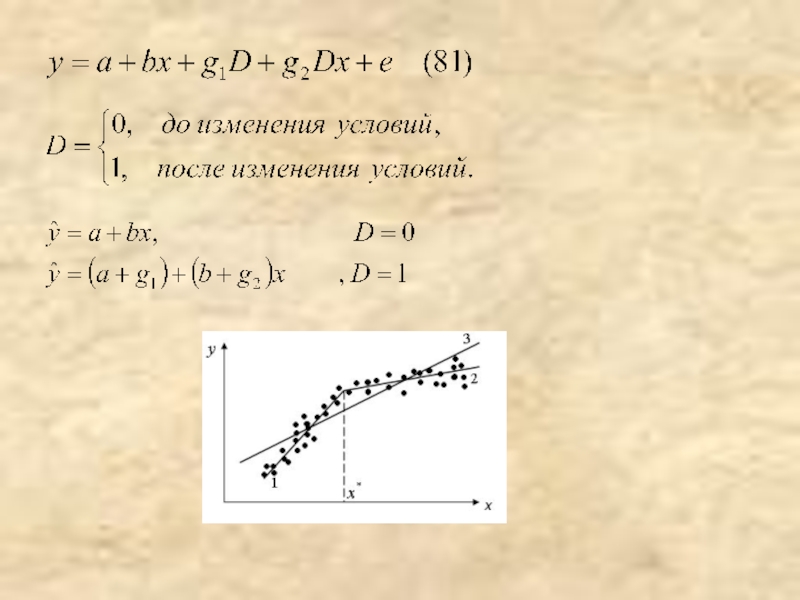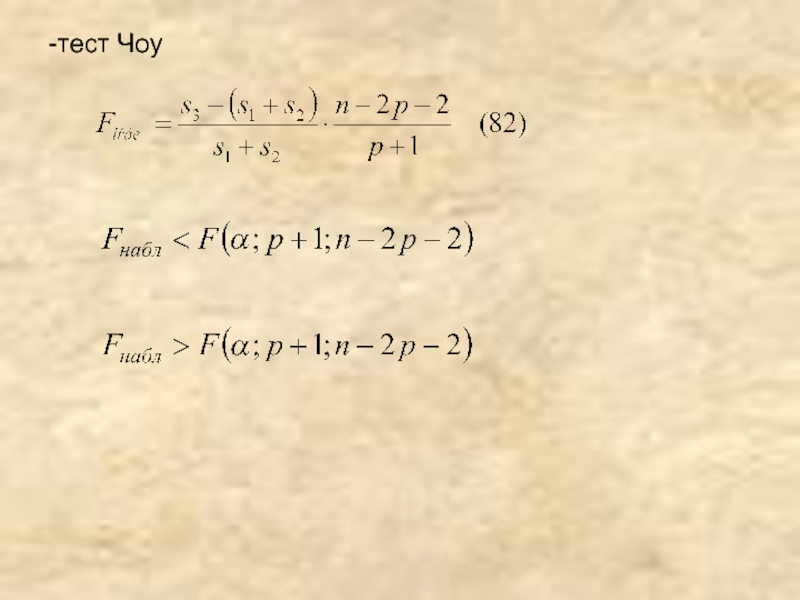Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множественная регрессия
Содержание
- 1. Множественная регрессия
- 2. Слайд 2
- 3. Матричный метод
- 4. S=[3;6;5;3,5;1,5]’ B=[a;b1;b2]’
- 5. Скалярный метод
- 6. Слайд 6
- 7. Регрессионная модель в стандартизованном масштабе
- 8. Слайд 8
- 9. Δ=0,926291; Δ1=0,688461; Δ2=-0,44504; β1=0,688461/0,926291=0,743245;β2=-0,44504/0,926291=-0,48045;
- 10. Слайд 10
- 11. Частные уравнения регрессии
- 12. Слайд 12
- 13. Слайд 13
- 14. Анализ качества эмпирического уравнения множественной линейной регрессии
- 15. H0 не отклоняется, параметр не значимH0 отклоняется, параметр значим
- 16. Слайд 16
- 17. - Н0 не отклоняется, на уровне α
- 18. Исключение k факторов:исключение оправданоисключение не оправданоН0 не отклоняется, исключение оправдано Н0 отклоняется, исключение не оправдано
- 19. Включение k факторов:включение не оправдановключение оправданоН0 не отклоняется, включение не оправданоН0 отклоняется, включение оправдано
- 20. Частный случай: добавление одного фактора- частный F – критерий
- 21. Показатель множественной корреляции
- 22. Показатель частной корреляции
- 23. Для двухфакторной модели
- 24. Процедуры пошагового отбора переменныхпроцедура последовательного присоединенияпроцедура последовательного присоединения – удаленияпроцедура последовательного удаления
- 25. Процедура «всех возможных регрессий»:Для заданного значения k
- 26. Таким образом:на первом шаге (k=1) находим один
- 27. Критерий останова (завершения) процедуры:выбирается такое оптимальное число
- 28. Гетероскедастичность-тест ранговой корреляции СпирменаН0 отклоняется, гетероскедас- тичность имеет место
- 29. -тест Голдфелда-Квандта
- 30. -метод «взвешенных наименьших квадратов»1.Дисперсии известны
- 31. 2.Дисперсии неизвестны
- 32. Слайд 32
- 33. Автокорреляция остатков
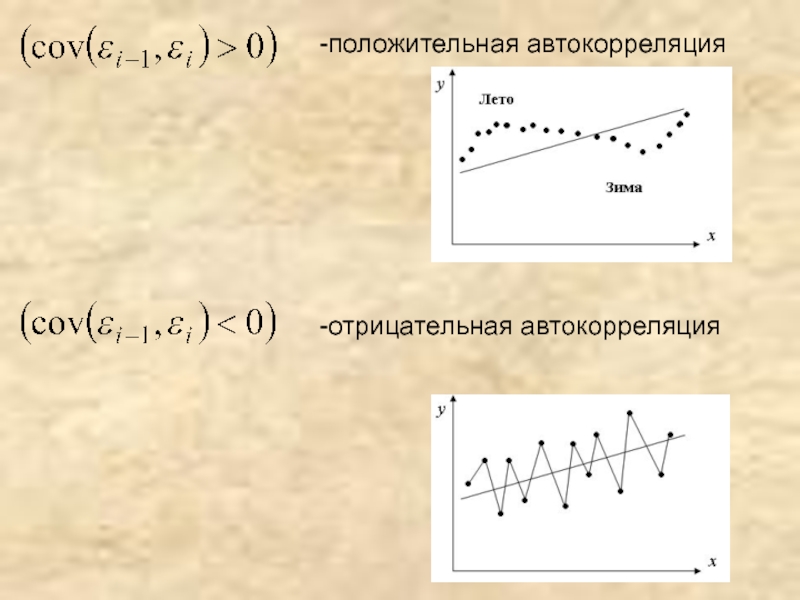
- 34. -положительная автокорреляция-отрицательная автокорреляция
- 35. -метод рядов-положительная автокорреляция-отрицательная автокорреляция-нет автокорреляции
- 36. -критерий Дарбина - Уотсона- положительная автокорреляция- зона неопределенности- автокорреляция отсутствует;- зона неопределенности;- отрицательная автокорреляция.
- 37. -авторегрессионная схема 1-го порядка AR(1)
- 38. Слайд 38
- 39. Фиктивные переменные в регрессионных моделях
- 40. Слайд 40
- 41. Слайд 41
- 42. -тест Чоу
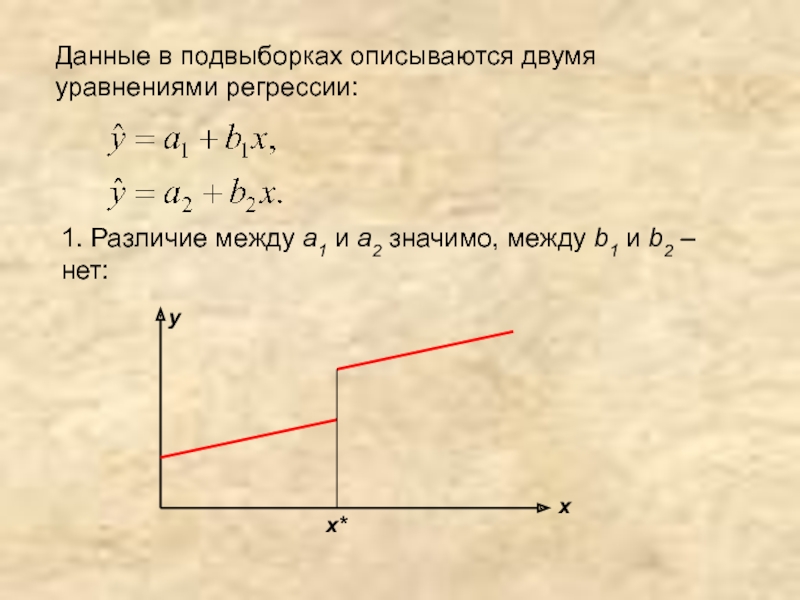
- 43. Данные в подвыборках описываются двумя уравнениями регрессии:1.
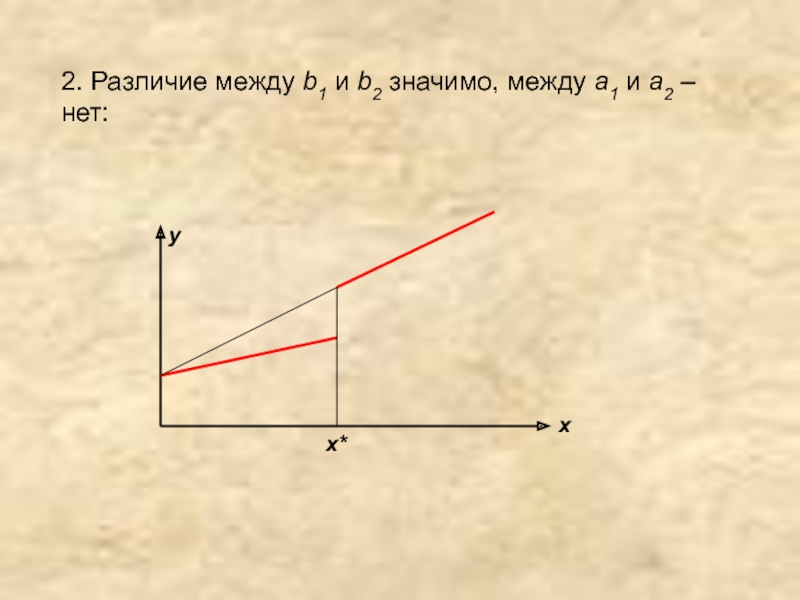
- 44. 2. Различие между b1 и b2 значимо, между a1 и a2 – нет:
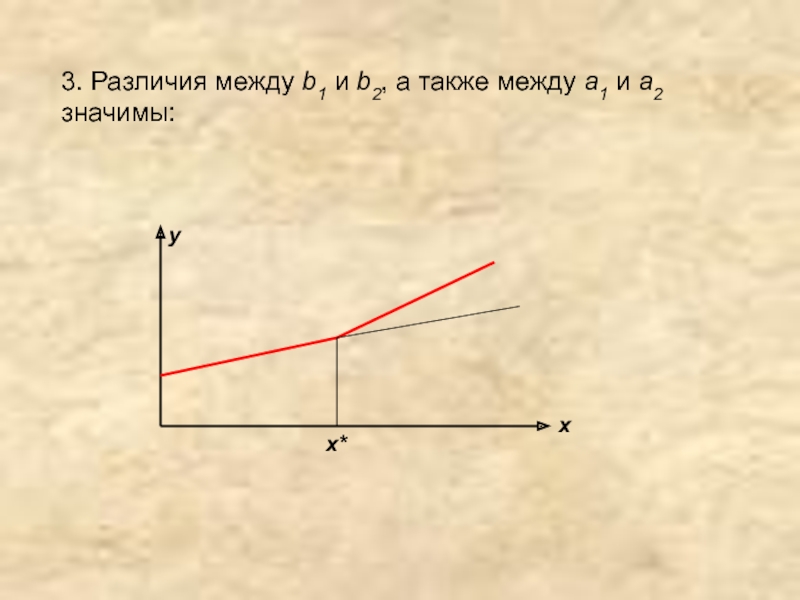
- 45. 3. Различия между b1 и b2, а также между a1 и a2 значимы:
- 46. - методика Гуйарати:
- 47. Скачать презентанцию
Матричный метод
Слайды и текст этой презентации
Слайд 9
Δ=0,926291; Δ1=0,688461; Δ2=-0,44504;
β1=0,688461/0,926291=0,743245;
β2=-0,44504/0,926291=-0,48045;
Слайд 17
- Н0 не отклоняется, на уровне α уравнение не значимо
-
Н0 отклоняется, на уровне α уравнение значимо
Слайд 18
Исключение k факторов:
исключение оправдано
исключение не оправдано
Н0 не отклоняется, исключение оправдано
Н0 отклоняется, исключение не оправдано
Слайд 19Включение k факторов:
включение не оправдано
включение оправдано
Н0 не отклоняется, включение не
оправдано
Н0 отклоняется, включение оправдано
Слайд 24Процедуры пошагового отбора переменных
процедура последовательного присоединения
процедура последовательного присоединения – удаления
процедура
последовательного удаления
Слайд 25Процедура «всех возможных регрессий»:
Для заданного значения k (k=1,2,…,p-1) проводится полный
перебор всех возможных комбинаций из k факторов (которые отобраны из
исходного набора x1, x2,…,xp). Определяются такие переменныедля которых коэффициент детерминации с результатом был бы максимальным.
Слайд 26Таким образом:
на первом шаге (k=1) находим один наиболее информативный фактор
(при условии, что в модель можно включать только один фактор
из первоначального набора)на втором шаге (k=2) определяется уже наиболее информативная пара факторов (из первоначального набора), имеющая наиболее тесную связь с результатом
на третьем шаге (k=3) будет отобрана наиболее информативная тройка факторов
и т.д.
Слайд 27Критерий останова (завершения) процедуры:
выбирается такое оптимальное число k0 факторов, на
котором нижняя доверительная граница коэффициента детерминации достигает своего максимума. Эта
граница вычисляется по формуле:

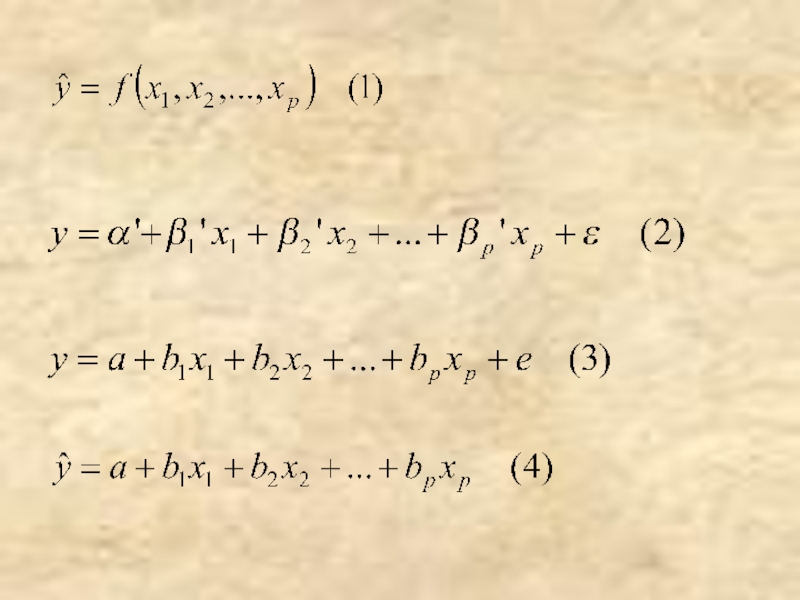

![Множественная регрессия S=[3;6;5;3,5;1,5]’ B=[a;b1;b2]’ S=[3;6;5;3,5;1,5]’ B=[a;b1;b2]’](/img/tmb/2/140861/7b58146f092a0d09c0ad772db6bf273f-800x.jpg)