Плоскость

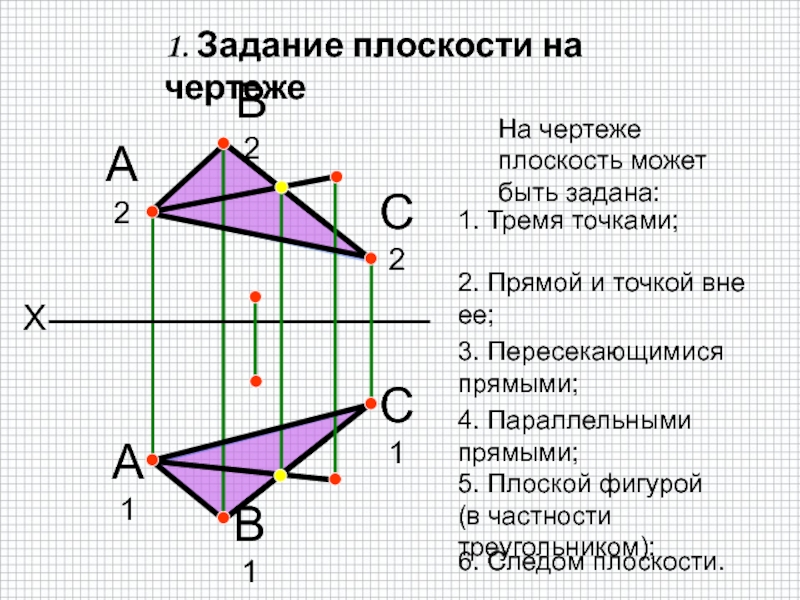
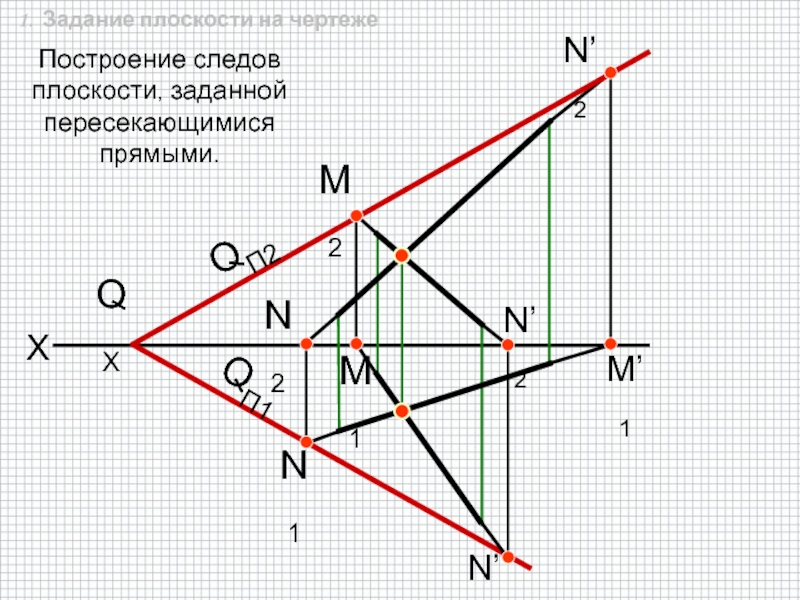
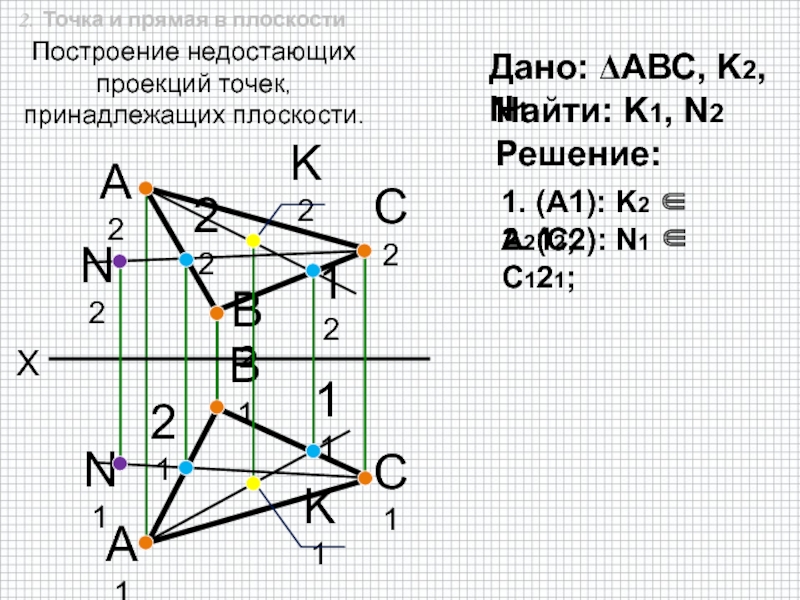
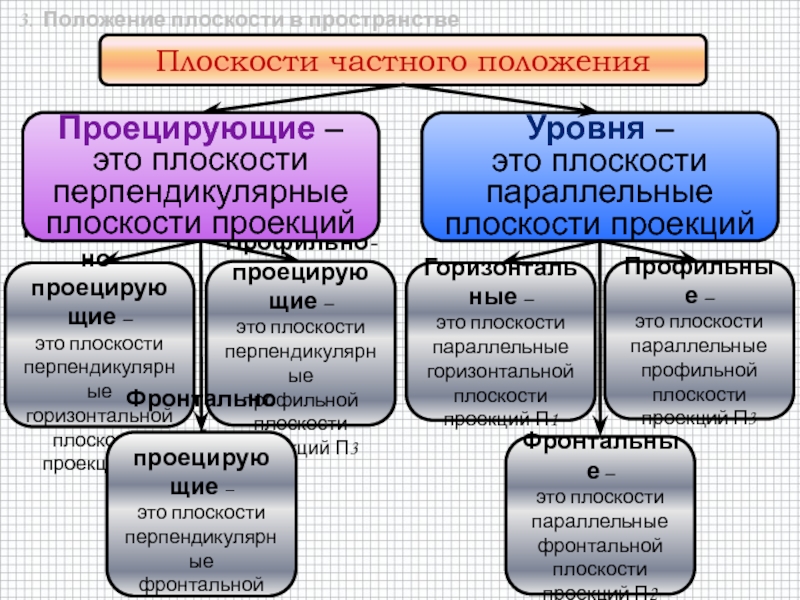
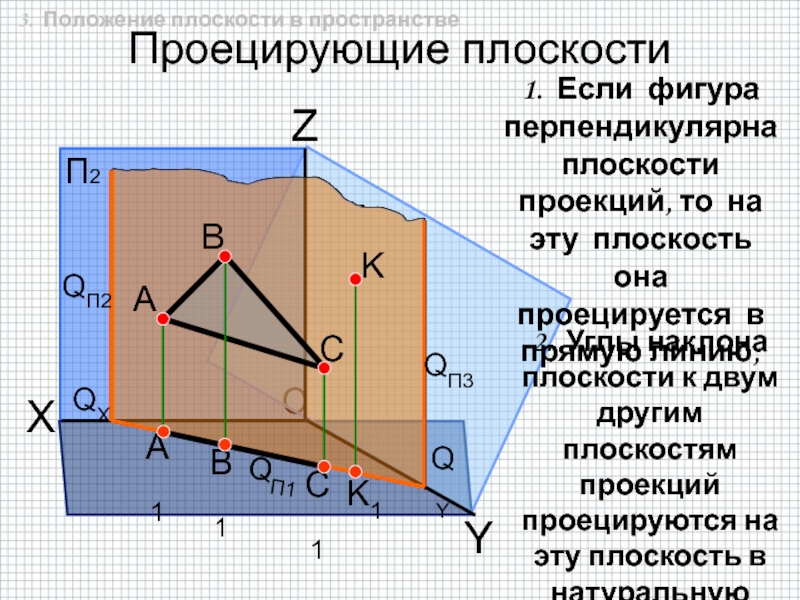
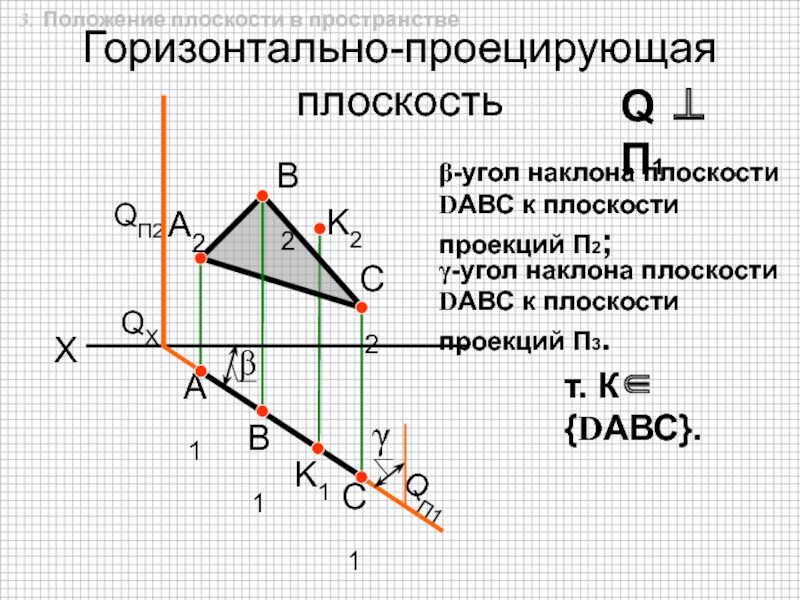
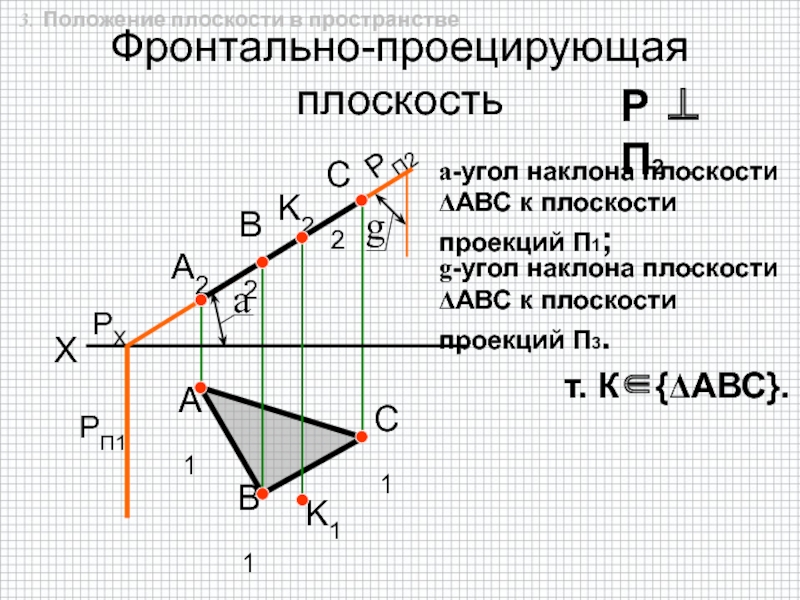
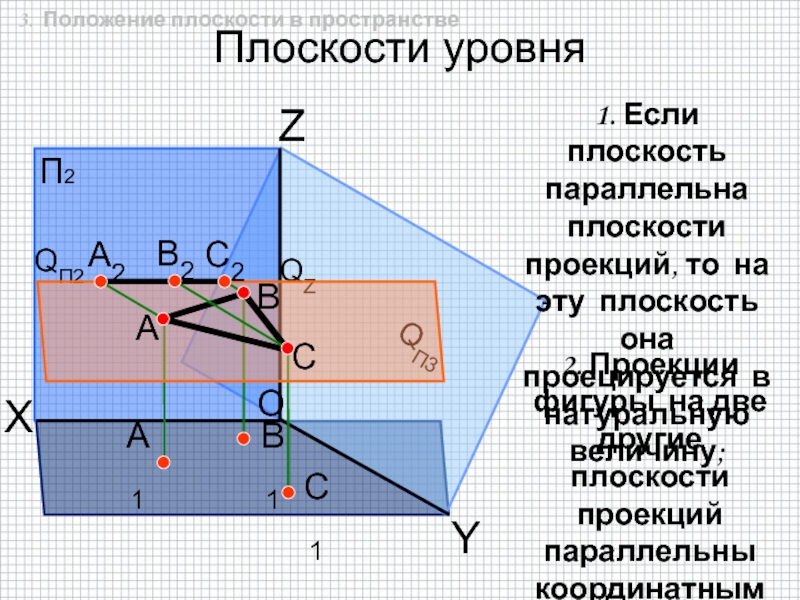
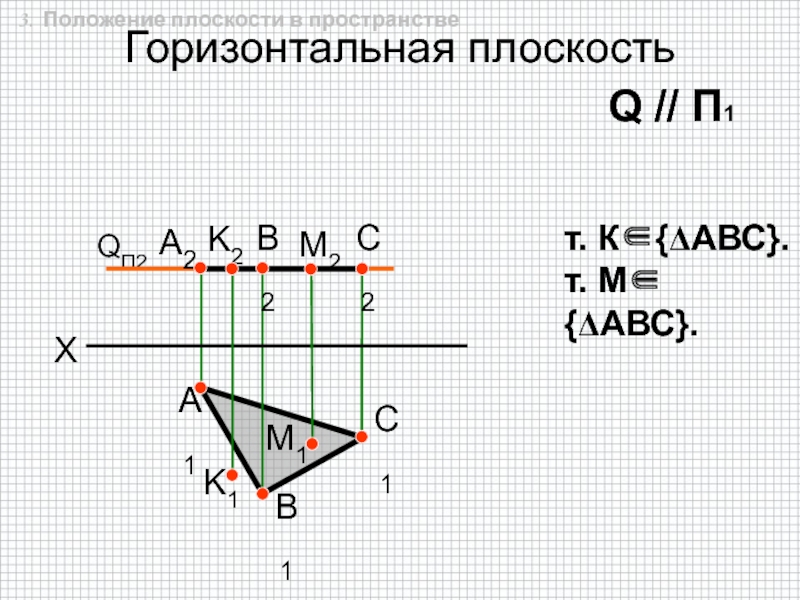
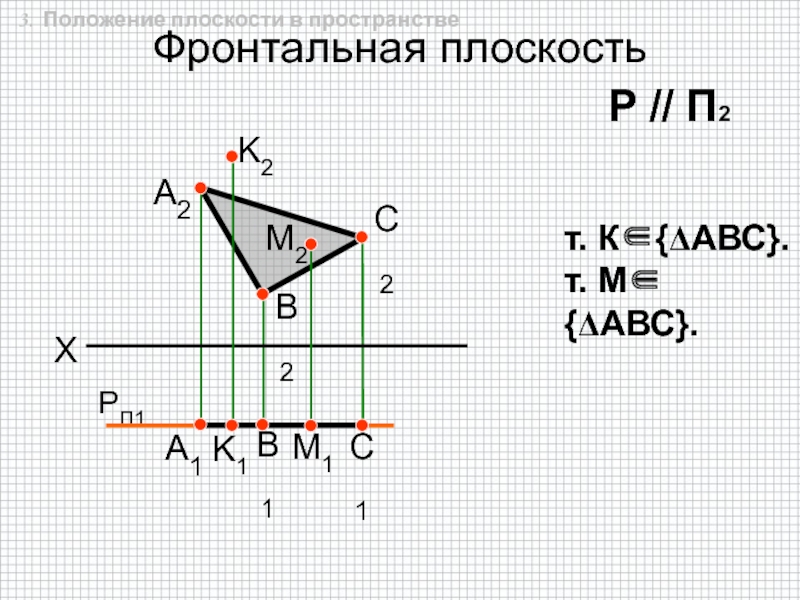
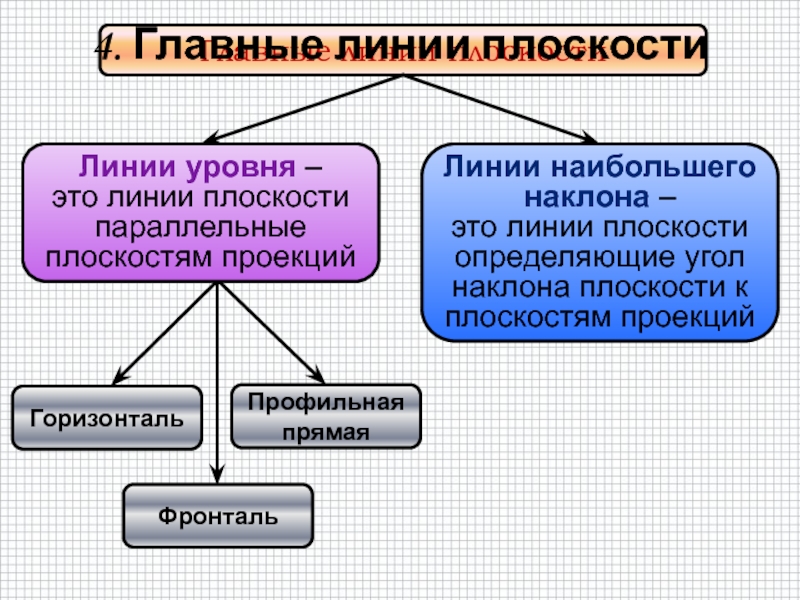
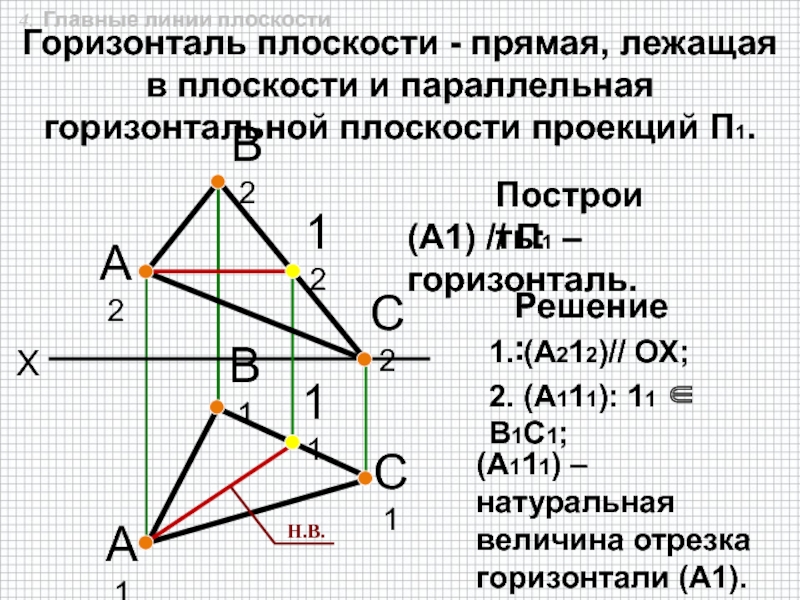
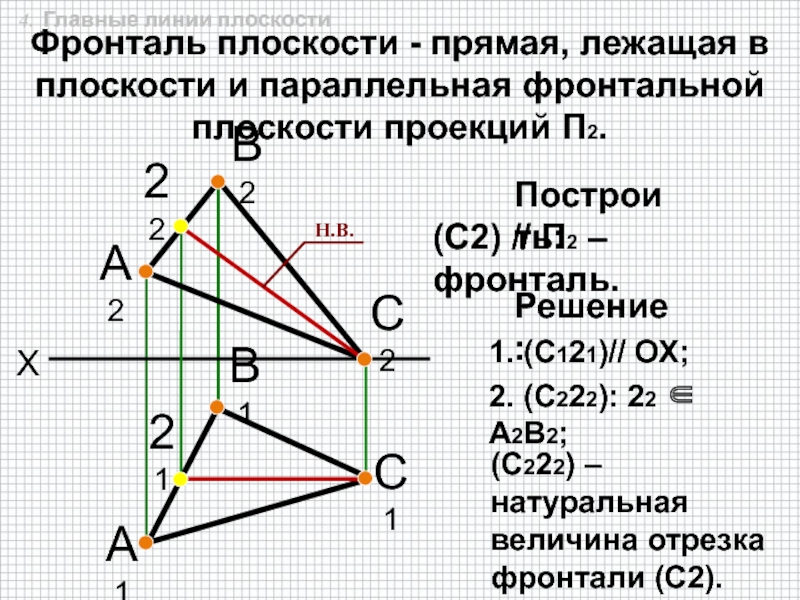
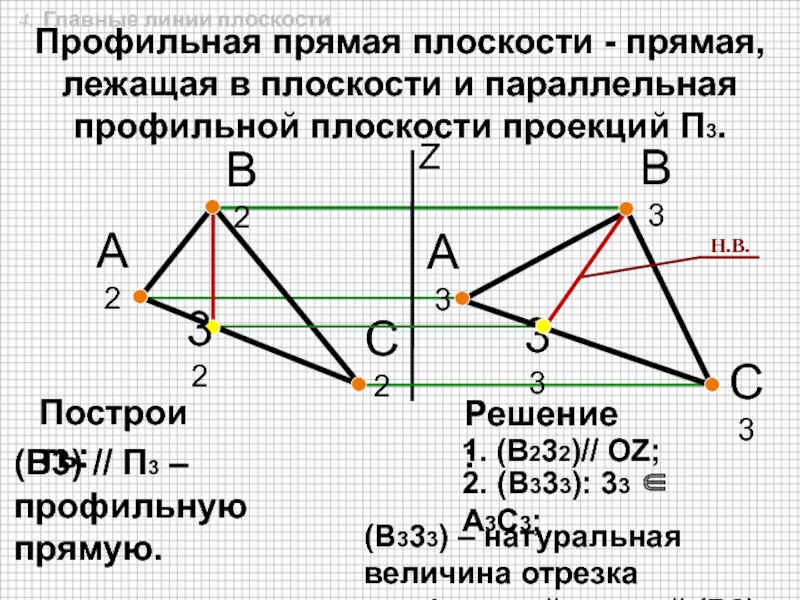
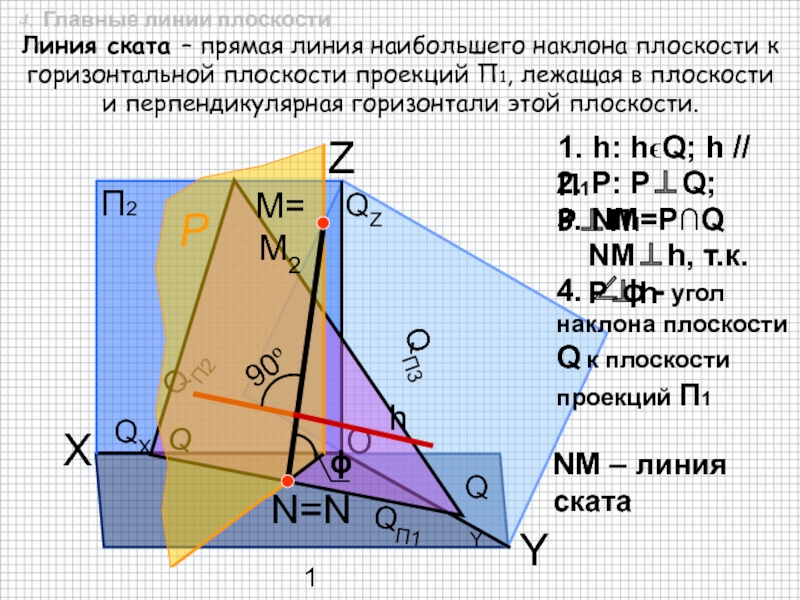
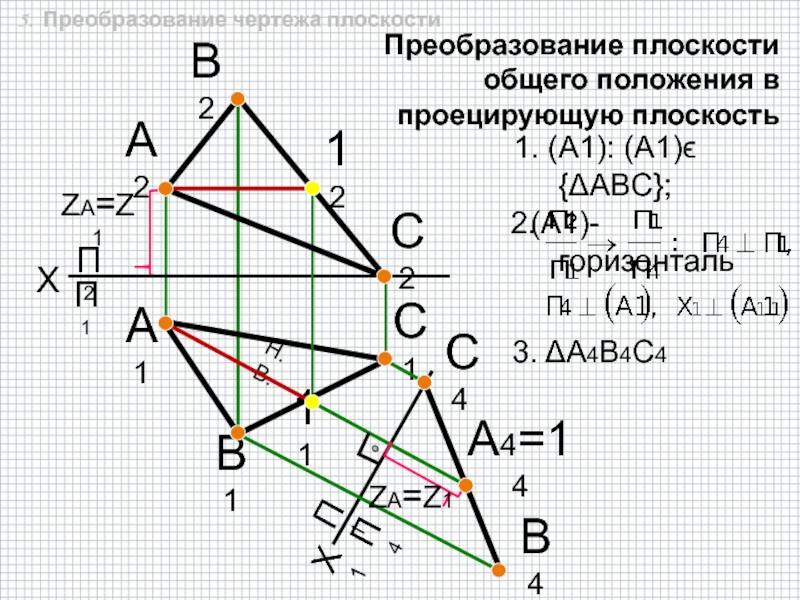
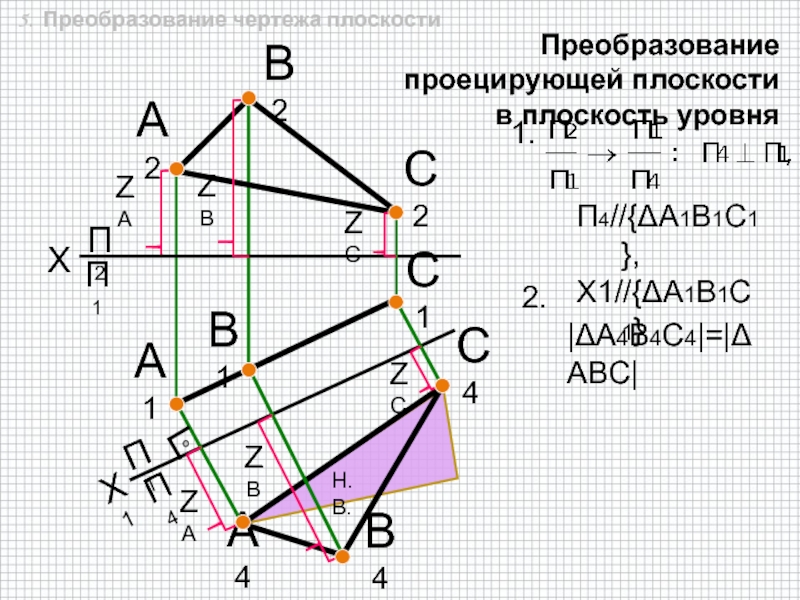
быть задана:
2. Прямой и точкой вне ее;


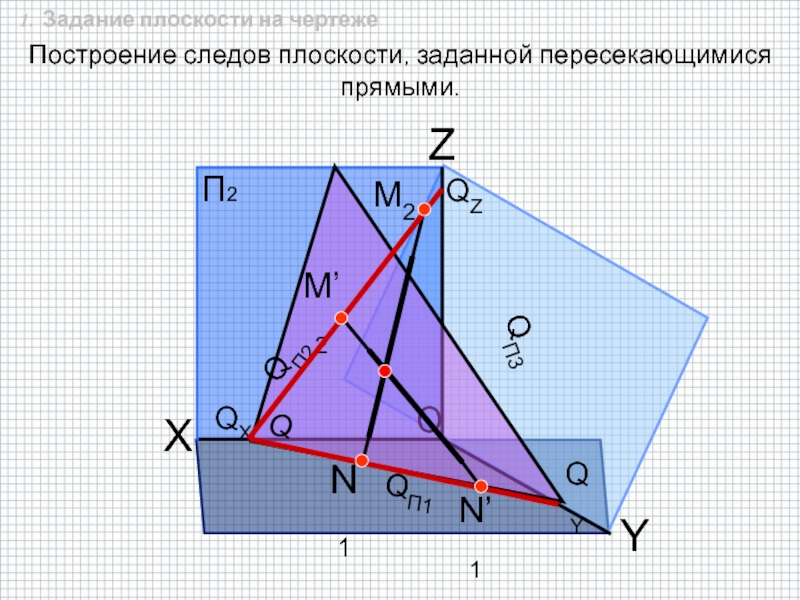
3. Пересекающимися прямыми;
4. Параллельными

5. Плоской фигурой (в частности треугольником);

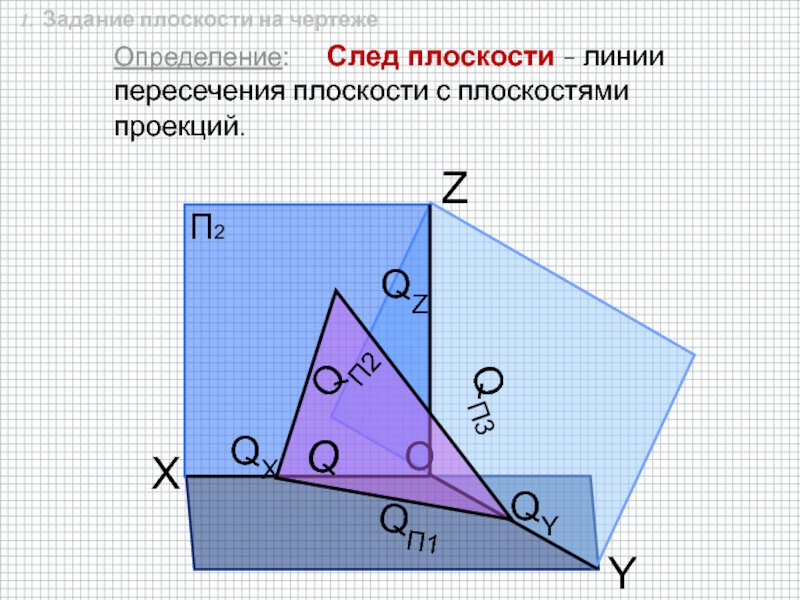
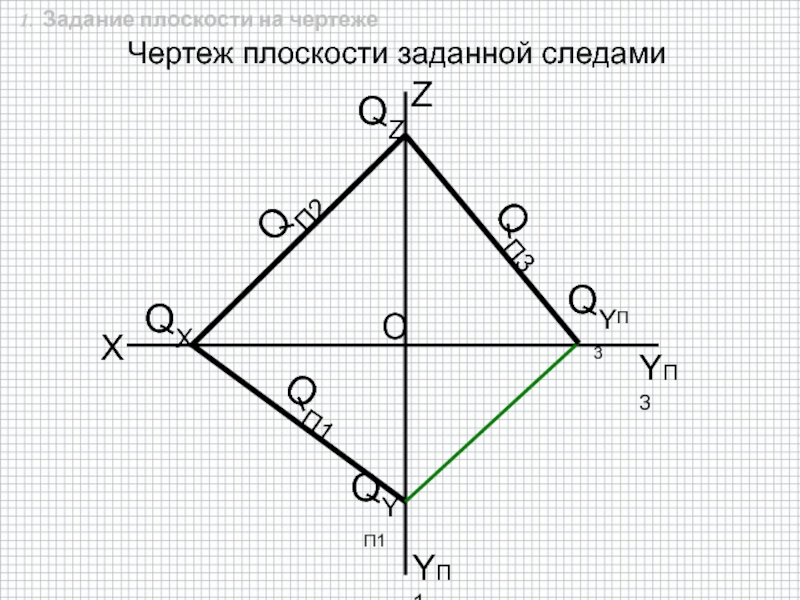
6. Следом плоскости.

плоскостями проекций.



O

П2
П1
П3
X
Y
Z
Q
QZ
QП2
QX
QП1
QY
QП3
1. Задание плоскости на чертеже

чертеже

чертеже

она принадлежит какой-либо прямой, лежащей в этой плоскости:

Прямая принадлежит плоскости, если:
1) она проходит через две точки, лежащие в данной плоскости:

или
2) она проходит через точку, принадлежащую плоскости, параллельно какой-нибудь прямой, лежащей в этой плоскости:

точек, принадлежащих плоскости.
Найти: K1, N2
Решение:
K2
N1



12
11

K1


2. (C2): N1 ∈ C121;

21

22



N2


2.

не перпендикулярная ни одной из плоскостей проекций, называется плоскостью общего

Плоскости, параллельные или перпендикулярные плоскостям проекций, называются плоскостями частного положения.

–
это плоскости
перпендикулярные
профильной
плоскости проекций П3
Фронтально-
проецирующие –
это плоскости
перпендикулярные
фронтальной
плоскости проекций П2
Горизонтальные –
это плоскости
параллельные
горизонтальной
плоскости

Профильные –
это плоскости
параллельные
профильной
плоскости проекций П3

Фронтальные –
это плоскости
параллельные
фронтальной
плоскости проекций П2

Проецирующие –
это плоскости
перпендикулярные
плоскости проекций

3. Положение плоскости в пространстве

плоскость она проецируется в прямую линию;
2. Углы наклона плоскости к

3. Положение плоскости в пространстве

П2;
γ-угол наклона плоскости DАВС к плоскости проекций П3.
т. К∈{DАВС}.
3.

П1;
g-угол наклона плоскости ΔАВС к плоскости проекций П3.
т. К∈{ΔАВС}.


3.

плоскость она проецируется в натуральную величину;
2. Проекции фигуры на две

B

C

A

A2

B2

C2

3. Положение плоскости в пространстве

пространстве

пространстве

проекций
Горизонталь
Профильная
прямая
Фронталь
Линии уровня –
это линии плоскости
параллельные
плоскостям проекций
4. Главные линии плоскости

параллельная горизонтальной плоскости проекций П1.


12
11


2. (A111): 11 ∈ В1С1;




(A1) //

(A111) – натуральная величина отрезка горизонтали (А1).

Построить:

Решение:

Н.В.

4. Главные линии плоскости

параллельная фронтальной плоскости проекций П2.


22
21


2. (С222): 22 ∈ А2В2;




(С2) //

(С222) – натуральная величина отрезка фронтали (С2).

Построить:

Решение:

Н.В.

4. Главные линии плоскости

и параллельная профильной плоскости проекций П3.


32
33
2. (B333): 33 ∈ А3C3;




(B3)

(B333) – натуральная величина отрезка профильной прямой (B3).

Построить:

Решение:

Н.В.

4. Главные линии плоскости

плоскости проекций П1, лежащая в плоскости и перпендикулярная горизонтали этой

Q

h

П1

M=M2

90º

ϕ

1. h: hϵQ; h // П1

2. Р: P⊥Q; P⊥П1

3. NM=P∩Q

NM⊥h, т.к. Р⊥h

4. ∠ϕ - угол наклона плоскости Q к плоскости проекций П1

NM – линия ската

4. Главные линии плоскости

может быть преобразована в:

плоскости
П2
Х1
П1
П4
А4=14
П1

ZА=Z1
Н.В.
X
А2
В2
А1
В1
С2
С1


12
11




1. (A1): (A1)ϵ{ΔABC};
(A1)-горизонталь
2.
3. ΔA4B4C4



В4
С4
ZА=Z1

2. |ΔA4B4C4|=|ΔABC|

В4
С4
ZА


В1


П4//{ΔA1B1C1},
Х1//{ΔA1B1C1}

ZB

ZB


ZC



ZC

плоскости
П2
Х1
П1
П4
А4
П1

ZА
X
А2
В2
А1
В1
С2
С1


h2
h1




1.


В4
С4
ZА

2.
П5//(A4B4C4)
П5
П4

ΔА
ΔА
А5

B5

C5
Н.В.





Х2

технического университета:

Бондарев Олег Александрович, к.т.н.,
Кайгородцева Наталья Викторовна, к.пед.н.

Авторы: