Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Relational Algebra
Содержание
- 1. Relational Algebra
- 2. CONTENTSQuery languages in DBProperties of binary operationsRelational
- 3. Query languagesLanguage categories:procedural (HOW to receive)nonprocedural (WHAT
- 4. Relational algebra closure and properties of binary
- 5. Relational algebra operationsBasic operations:set-theoretic (union, intersection, difference)projectionselectioncartesian product, joindivisionAdditional operationsassignmentrenaminggeneralized projectionouter join…
- 6. Set-theoretic operationsTwo relations R and S are
- 7. Union operation Union of two compatible relations
- 8. Difference operation Difference of two compatible relations
- 9. Intersection operationIntersection of two compatible relations R
- 10. Projection operationProjection of the relation R with
- 11. θ-comparability of attributes and tuplesLet’s θ is
- 12. Selection (restriction) operationLet’s М and N are
- 13. Cartesian productCartesian product of two rations R
- 14. Join operation Let us M and N
- 15. Join and natural joinJoin on a condition
- 16. SemijoinSemijoin is join of two relations with
- 17. Image of the tupleImage of the relation
- 18. Division operation (1)Division of two relations R(M,N)
- 19. Division operation(2)Example:R
- 20. FAC (FNo, Name, Dean, Bld, Fund)DEP (DNo,
- 21. Examples of queries in RA (1)Projection: Output
- 22. Examples of queries in RA (2)Composition of
- 23. Examples of queries in RA (3)Basic query
- 24. Examples of division operation1) Output teacher numbers that
- 25. Additional operations Additional operationsAssignmentRenamingGeneralized projectionOuter join…
- 26. Assignment operationThe assignment operation (←) provides a
- 27. Rename operationThe rename operation allows us to
- 28. Generalized projection operationExtends the projection operation by
- 29. Outer joinOuter join is an extension of
- 30. Outer join – example of ordinary join1)
- 31. Left outer joinFAC FNo Name
- 32. Right outer joinFAC FNo Name
- 33. Full outer join4) Full outer join
- 34. Equivalent transformations of relational expressions1) Commutativity
- 35. Optimization of RA expressionsR(A,B) S(C,D)
- 36. General rules of RA expressions optimizationGeneral rules
- 37. Relational Algebra: SummaryRelational Algebra: Formal language for
- 38. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Lecture 6. Relational algebra
National Aviation University
Computer Science Faculty
Department of Software
Engineering
Слайд 2CONTENTS
Query languages in DB
Properties of binary operations
Relational algebra operations
Examples
Equivalent
transformation and optimization of relational algebra expressions
Слайд 3Query languages
Language categories:
procedural (HOW to receive)
nonprocedural (WHAT to receive)
Formal languages:
relational
algebra
relational calculus (tuple-oriented and domain-oriented)
Query language is a language that
allows to extract data from database.Formal languages are basis for creation of DB query languages (Alpha, QUEL, QBE, SQL)
Слайд 4Relational algebra closure and properties of binary operations
Algebra = data
(of the defined type) + operations. Algebra is closured if result
of any operation are the same type as a data in argument. Closure property allows to embed operations in each other.Relational algebra = relations + operations.
Relational algebra closured.
Property of binary relations:
Operation ϕ is commutative if А ϕ В = B ϕ A
Operation ϕ is associative if (А ϕ В) ϕ С = А ϕ (В ϕ С)
Operation ϕ is distributive with respect with other operation θ, if
А ϕ (В θ С ) = (А ϕ В) θ (А ϕ С)
Слайд 5Relational algebra operations
Basic operations:
set-theoretic (union, intersection, difference)
projection
selection
cartesian product,
join
division
Additional operations
assignment
renaming
generalized
projection
outer join
…
Слайд 6Set-theoretic operations
Two relations R and S are (union) compatible if:
R
and S have the same arity/ that is they have
the same number of attributes.Domains of corresponding attributes are compatible (the 1-st attribute of R is defined on the same domain as the 1-st attribute of S and so on) .
Set-theoretic operations require compatibility of their operands
Слайд 7Union operation
Union of two compatible relations R and S
with schemas R(A) and S(A), where A is a set
of attributes, is the relation T with schema T(A) that contains tuples of both relations, but without duplicates.The operation commutative, associative and distributive with respect to the intersection .
Example:
Слайд 8Difference operation
Difference of two compatible relations R and S
with schemas R(A) and S(A), where A is a set
of attributes, is the relation T with schema (A) that contains only those tuples of the relation R, which are not present in the relation S.The operation not commutative and associative and distributive.
Т(А) = R(А) ⎯ S(А) = {t | t ∈ R & t ∉ S}
Example:
Note: Relational algebra do not use set-theoretic complement operation!!!
Слайд 9Intersection operation
Intersection of two compatible relations R and S with
schemas R(A) and S(A), where A is a set of
attributes, is the relation T with schema T(A) that contains tuples which simultaneously present in both relations.The operation commutative, associative and distributive with respect to union.
Т(А) = R(А) ∩ S(А) = {t | t ∈ R & t ∈ S}
Example:
Intersection is expressed via difference: R ∩ S = R – (R – S)
Слайд 10Projection operation
Projection of the relation R with schema R(A), where
A is a set of attributes, with respect to the
set of attributes В, where В ⊂ А, is a such relation S with the schema S(B) that contains tuples of the relation R by deleting from them values that belong attributes A - B.S(B) = R[B] = {t[B] ⏐ t ∈ R}
Projection is denoted as: R[B] или πВ(R)
Example:
Note: Duplicate tuples are deleted
Слайд 11θ-comparability of attributes and tuples
Let’s θ is any of the
following comparison operators : =, ≠, < ≤, >, ≥.
The attributes A and B the same or different relations are θ-comparable, if for any values a ∈ A and b ∈ B expression а θ b is defined.Set of attributes М = (A1,…, Ak) and N = (B1,…,Bn) are
θ-comparable, if k = n and (Ai, Bi) are θ‑comparable. In this case expression M θ N means the following:
M θ N = (A1 θ B1) & … & (Ak θ Вk)
If t is a relation tuple, that contains sets of θ‑comparable attributes M and N, then the notation t[M] θ t[N] means the following:
(t[A1] θ t[B1]) & … & (t[Ak] θ t[Вk]).
Слайд 12Selection (restriction) operation
Let’s М and N are sets of θ-comparable
attributes of the relation R with schema R(A). Then selection
(restriction) of the relation R on condition М θ N, denoted as R [М θ N], is such relation T with schema T(A), which tuples satisfy the condition t[М] θ t[N].Т(А) = R[M θ N] = {t | t ∈ R & t[M] θ t[N]}
Example:
The operation also has the following notation: σM θ N(R)
One of the attributes set M or N may be constant.
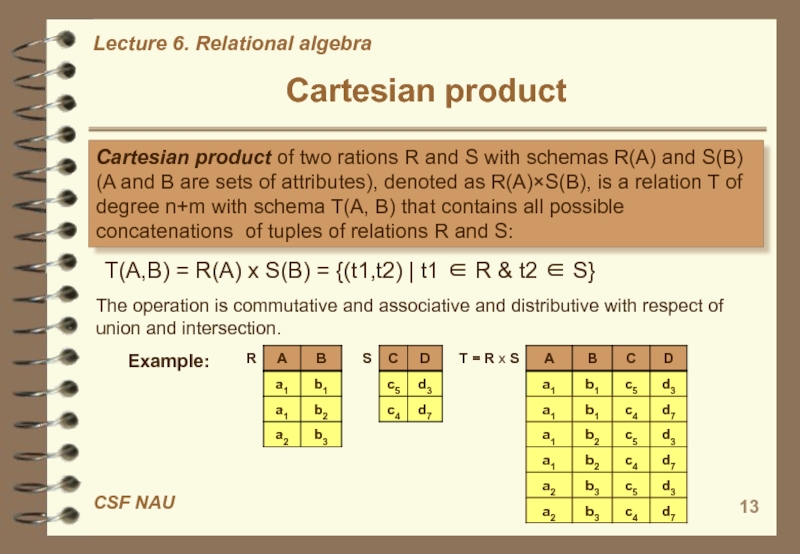
Слайд 13Cartesian product
Cartesian product of two rations R and S with
schemas R(А) and S(B) (A and B are sets of
attributes), denoted as R(A)×S(B), is a relation T of degree n+m with schema T(А, B) that contains all possible concatenations of tuples of relations R and S:The operation is commutative and associative and distributive with respect of union and intersection.
Т(А,В) = R(А) x S(B) = {(t1,t2) | t1 ∈ R & t2 ∈ S}
Example:
Слайд 14Join operation
Let us M and N are sets of
θ-comparable attributes. Join of the relations R and S with
schemas R(A,M) and S(N,B) on a condition М θ N, denoted as R[М θ N]S, is a relation T with a schema T(A,M,N,B) which tuples are concatenation only those tuples of R and S, for which sets of attributes N and M satisfy condition М θ N.T = R[М θ N]S = {(t1, t2) ⏐ t1 ∈ R ∧ t2 ∈ S ∧ t1[М] θ t2[N]}
Example:
The operation commutative and associative
The operation is also denoted as: R M θ NS
Join is expressed via the product and the selection:
R M θ NS = σM θ N(R x S)
Слайд 15Join and natural join
Join on a condition of equality (=)
is called as equi-join .
Natural join is a join
on equality condition by attributes with the same names with deleting in the result relation one of the compared set of attributes. Natural join is denoted by the symbol * (for example R*S).
Example:
R S R[B,C=B,C]S R*S
Слайд 16Semijoin
Semijoin is join of two relations with deleting from the
resulting relation attributes of one of the joined relations.
Semijoin
is denoted as: R[M θ N)SR[М θ N)S = {(t1) ⏐ t1 ∈ R ∧ t2 ∈ S ∧ t1[М] θ t2[N]}
Example:
R S R[B,C=B,C)S
R[М θ N)S = (R[М θ N]S)[A] – where А is a set of attributes of the relation R
Semijoin is expressed via the join and projection in such a way:
Слайд 17Image of the tuple
Image of the relation R(M,N) with respect
the tuple t1 ∈ R[M], that is denoted as It1(R),
is the set of such tuples t2 ∈ R[N], that concatenation of tuples (t1,t2) belongs to the relation R.It1 ∈ R[M](R) = {(t2) ⏐ t2 ∈ R[N] ∧ (t1,t2) ∈ R}
Examples:
R Ia1∈ R[A](R) Ia2∈ R[A](R) I(a1,b1)∈ R[A,B](R) Ic2∈ R[C](R)
Слайд 18Division operation (1)
Division of two relations R(M,N) and S(K,L) with
respect of set of compatible attributes N and M, denoted
as R [N ÷ K] S, is a relation T(M) with such tuples t ∈ R[M] whose images It(R) contain all tuples of the projection S[K].T(M) = R[N÷K]S = {t ⏐t ∈ R[M] & It(R) ⊇ S[K]}
The operation allows to formulate queries like this:
- Output teachers that teach lectures of ALL types.
Слайд 19Division operation(2)
Example:
R
S
S[C] R[C÷C]SDivision operation is expressed by other operations of RA:
R[N÷K]S = R[M] – ((R(M) x S[K]) – R)[M]
Division operation is not commutative and associative
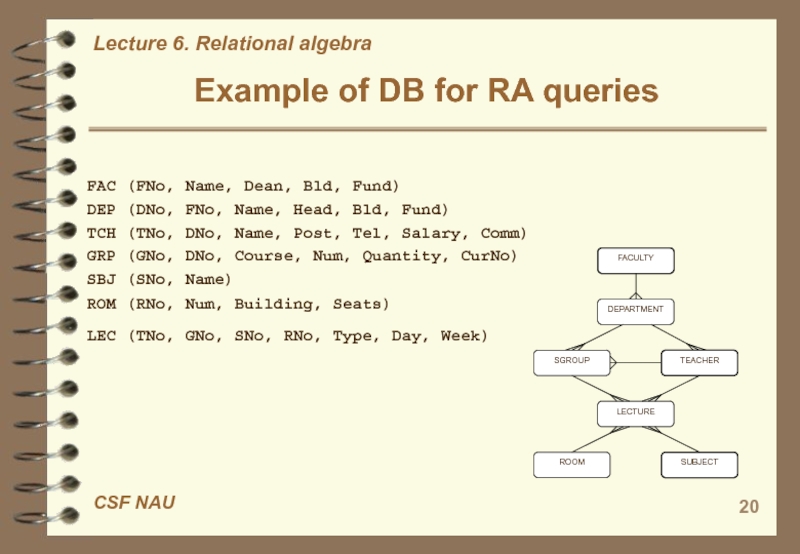
Слайд 20FAC (FNo, Name, Dean, Bld, Fund)
DEP (DNo, FNo, Name, Head,
Bld, Fund)
TCH (TNo, DNo, Name, Post, Tel, Salary, Comm)
GRP (GNo,
DNo, Course, Num, Quantity, CurNo)SBJ (SNo, Name)
ROM (RNo, Num, Building, Seats) LEC (TNo, GNo, SNo, RNo, Type, Day, Week)
Example of DB for RA queries
Слайд 21Examples of queries in RA (1)
Projection: Output list jf teacher
names and posts:
TCH[Name, Post] πName,Post(TCH)
Selection: Output information about CSF faculty:
FAC[Name =
‘CSF’] σName=‘CSF’(FAC)Join: Output information about faculries and their departments:
FAC[FNo = FNo]DEP FAC FNo=FNoDEP
Слайд 22Examples of queries in RA (2)
Composition of join, selection and
projection
1) Outputs names of faculties and their departments
(FAC[FNo = FNo]DEP)
[FAC.Name, DEP.Name]
πFAC.Name, DEP.Name(FAC FNo=FNoDEP)2) Outputs names of faculties with fund > 1000 and their departments :
((FAC[Fund > 1000])[FNo = FNo]DEP) [FAC.Name, DEP.Name] πFAC.Name, DEP.Name((σFund >1000(FAC)) FNo=FNoDEP)
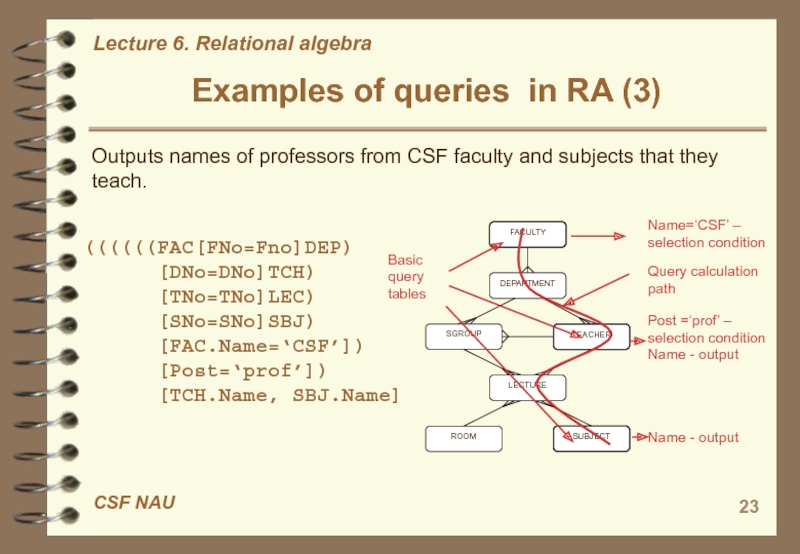
Слайд 23Examples of queries in RA (3)
Basic query tables
Name=‘CSF’ – selection
condition
Query calculation path
Post =‘prof’ – selection condition
Name - output
Name -
outputOutputs names of professors from CSF faculty and subjects that they teach.
((((((FAC[FNo=Fno]DEP)
[DNo=DNo]TCH)
[TNo=TNo]LEC)
[SNo=SNo]SBJ)
[FAC.Name=‘CSF’])
[Post=‘prof’])
[TCH.Name, SBJ.Name]
Слайд 24Examples of division operation
1) Output teacher numbers that teach in ALL
groups:
((LEC[TNo,GNo])[GNo÷GNo]GRP)[TNo]
2) Output teacher numbers that teach in ALL groups of
the first course:((LEC[TNo,GNo])[GNo÷GNo](GRP[Course=1]))[TNo]
3) Output teacher names that teach in ALL groups of the first course:
(((LEC[TNo,GNo])[GNo÷GNo](GRP[Course=1])) [TNo=TNo]TCH)[TCH.Name]
LEC(GNo,TNo,...)
GRP(GNo, Course...)
TCH(TNo, Name...)
Слайд 25Additional operations
Additional operations
Assignment
Renaming
Generalized projection
Outer join
…
Слайд 26Assignment operation
The assignment operation (←) provides a convenient way to
express complex queries, write query as a sequential program consisting
of a series of assignments by using intermediate temporal relations followed by an expression whose value is displayed as a result of the query.Пример: Output teacher names that teach in ALL groups of the first course:
(((LEC[TNo,GNo])[GNo÷GNo](GRP[Course=1])) [TNo=TNo]TCH)[TCH.Name]
Temp1 ← LEC[TNo,GNo]
Temp2 ← GRP[Course=1]
Temp3 ← Temp1[GNo÷GNo]Temp2
Temp4 ← Temp3[TNo=TNo]TCH
Temp4[TCH.Name]
Слайд 27Rename operation
The rename operation allows us to name, and therefore
to refer to, the results of relational-algebra expressions.
It has the
following syntax:ρR(A1,A2,...,An)(E)
Where: Е – relational algebra expression,
R(A1,A2,...,An) – name of the relation ant its attributes that is calculated by expression E.
Example: Output names of faculties and their departments. Rezulted relation should have name FAC_DEP with attributes FName и DName respectively:
ρFAC_DEP(FName,DName)(FAC[FNo=FNo]DEP)[FAC.Name,DEP.Name]
Слайд 28Generalized projection operation
Extends the projection operation by allowing arithmetic functions
to be used in the projection list.
R[F1, F2,...,Fn] πF1, F2,...,Fn(R)
Where: R –
relation or expression of relational algebra;F1, F2,...,Fn – are arithmetic expressions involving constants and attributes in the schema of E.
Example: Output teacher names and their salary + commission
TCH[Name, Salary + Commission]
Слайд 29Outer join
Outer join is an extension of the join operation
that avoids loss of information.
Computes the join and then adds
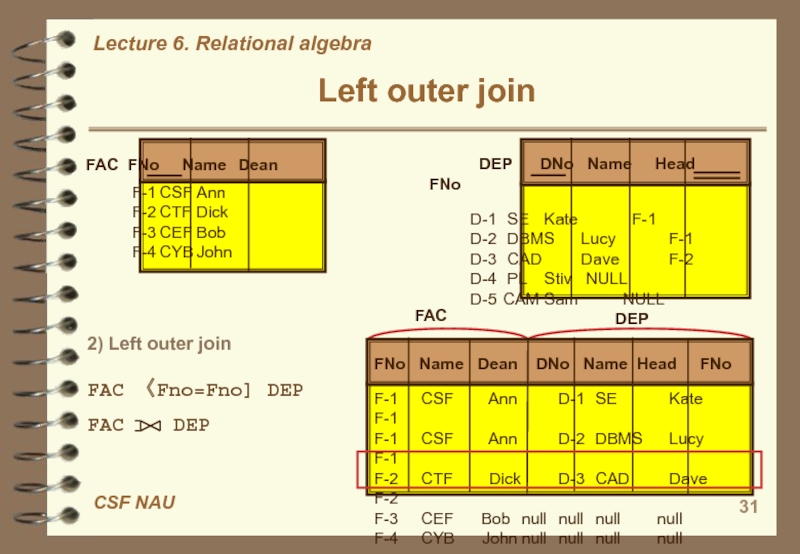
tuples form one relation that does not match tuples in the other relation to the result of the join. Слайд 31Left outer join
FAC FNo Name Dean
F-1 CSF Ann
F-2 CTF Dick
F-3 CEF Bob
F-4 CYB John
DEP DNo Name Head FNoD-1 SE Kate F-1 D-2 DBMS Lucy F-1 D-3 CAD Dave F-2 D-4 PL Stiv NULL D-5 CAM Sam NULL
2) Left outer join
FAC 〈Fno=Fno] DEP
FAC DEP
FNo Name Dean DNo Name Head FNo
F-1 CSF Ann D-1 SE Kate F-1
F-1 CSF Ann D-2 DBMS Lucy F-1
F-2 CTF Dick D-3 CAD Dave F-2
F-3 CEF Bob null null null null
F-4 CYB John null null null null
FAC
DEP
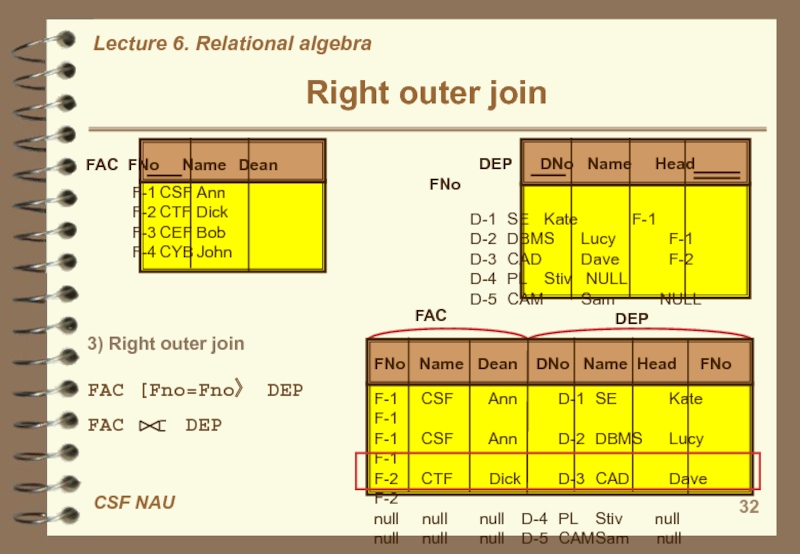
Слайд 32Right outer join
FAC FNo Name Dean
F-1 CSF Ann
F-2 CTF Dick
F-3 CEF Bob
F-4 CYB John
DEP DNo Name Head FNoD-1 SE Kate F-1 D-2 DBMS Lucy F-1 D-3 CAD Dave F-2 D-4 PL Stiv NULL D-5 CAM Sam NULL
3) Right outer join
FAC [Fno=Fno〉 DEP
FAC DEP
FNo Name Dean DNo Name Head FNo
F-1 CSF Ann D-1 SE Kate F-1
F-1 CSF Ann D-2 DBMS Lucy F-1
F-2 CTF Dick D-3 CAD Dave F-2
null null null D-4 PL Stiv null
null null null D-5 CAM Sam null
FAC
DEP
Слайд 33Full outer join
4) Full outer join
FAC 〈Fno=Fno〉 DEP
FAC
DEP
FNo Name Dean DNo Name
Head FNoF-1 CSF Ann D-1 SE Kate F-1 F-1 CSF Ann D-2 DBMS Lucy F-1 F-2 CTF Dick D-3 CAD Dave F-2 F-3 CEF Bob null null null null F-4 CYB John null null null null null null null D-4 PL Stiv null null null null D-5 CAM Sam null
FAC
DEP
Inner join
Left outer join
Right outer join
Full outer join
Слайд 34Equivalent transformations of
relational expressions
1) Commutativity of selection: σF(σG(R))=σG(σF(R))=σF&G(R)
2) Commutativity
of selection and projection:
πG(σF(R))=σF(πG(R))=σF&G(R), если G ⊇ F
3) Distributivity of
selection and product
σF(R х S) = σF(R) x σF(S)
4) Distributivity of selection and set-theoretic operations:
σF(R ∪ S)=σF(R) ∪ σF(S), σF(R ∩ S)=σF(R) ∩ σF(S)
5) Distributivity of selection and join:
σF(R S) = σF(R) S, если условие F относится к R
6) Distributivity of projection and set-theoretic operations :
πF(R ∪ S)=πF(R) ∪ πF(S), πF(R ∩ S)=πF(R) ∩ πF(S)
Слайд 35
Optimization of RA expressions
R(A,B) S(C,D) R(A,B)
S(C,D) RA,B) S(C,D)
R(A,B) S(C,D) × × ×
σD=9
σB=C & D=9 σB=C σB=C B=C
σD=9
πA
πA
πA
πA
πA(σB=C & D=9(R(A, B)x S(C,D)))
Слайд 36General rules of RA expressions optimization
General rules of RA expressions
optimization:
Transform each selection σF1&...&Fn(E) to the sequence of
selections σF1(...
σFn(E))
Move each selection downwards of the tree as far as it is possible (thus (vertical) size of the relation is reduced).
Adjacent selection and cartesian product are replaced by join.
Move each projection downwards of the tree as far as it is possible (thus (horizontal) size of the relation is reduced).
Transform each cascade of adjacent selections and projections into single projection or selection with subsequent projection
Слайд 37Relational Algebra: Summary
Relational Algebra:
Formal language for handling data in
relational model
Procedural language, how to retrieve data
No practical
relevance for querying DBFormal basis for query optimization
Important terms & concepts:
Union R ∪ S, difference R – S, intersection R ∩ S
Projection π
Selection σ
Cartesian product R x S
Joins R
Difference















![Relational Algebra Image of the tupleImage of the relation R(M,N) with respect the Image of the tupleImage of the relation R(M,N) with respect the tuple t1 ∈ R[M], that is](/img/thumbs/9c09a014c68d3bac8a89ccf61d720fdd-800x.jpg)


![Relational Algebra Examples of queries in RA (1)Projection: Output list jf teacher names Examples of queries in RA (1)Projection: Output list jf teacher names and posts: TCH[Name, Post] πName,Post(TCH)Selection: Output information about](/img/thumbs/df7aa2058dccf0b3131fd66611ab84c6-800x.jpg)

![Relational Algebra Examples of division operation1) Output teacher numbers that teach in ALL groups: ((LEC[TNo,GNo])[GNo÷GNo]GRP)[TNo] Examples of division operation1) Output teacher numbers that teach in ALL groups: ((LEC[TNo,GNo])[GNo÷GNo]GRP)[TNo] 2) Output teacher numbers that teach](/img/tmb/2/141533/1de7414d2a8f077d1dde110c4deb0016-800x.jpg)





![Relational Algebra Outer join – example of ordinary join1) Ordinary join (inner join)FAC [Fno=Fno] DEPFAC DEP Outer join – example of ordinary join1) Ordinary join (inner join)FAC [Fno=Fno] DEPFAC](/img/tmb/2/141533/c3b93bdf1479d6be7d0677b4dc00b284-800x.jpg)