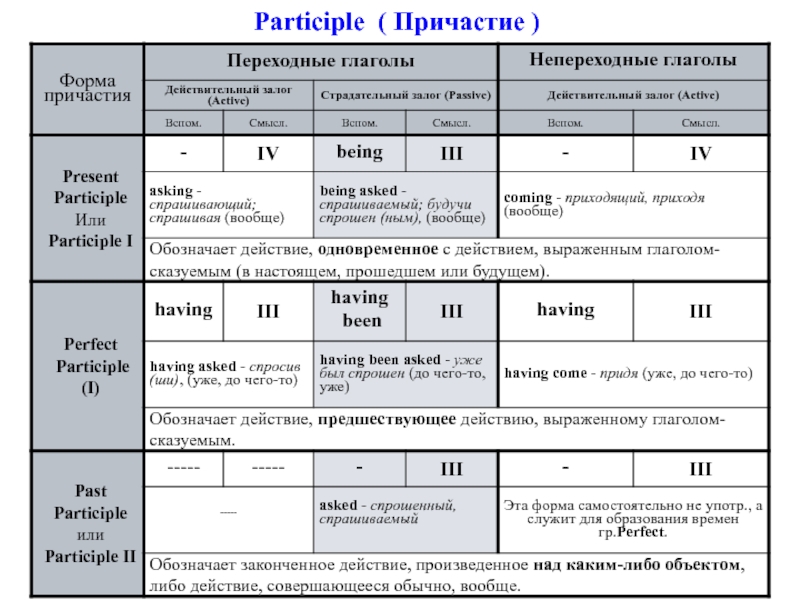
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Normalization Theory
Содержание
- 1. Normalization Theory
- 2. Monday, August 12, 2019CONTENTSWhat is the purpose
- 3. Monday, August 12, 2019What is the purpose
- 4. Monday, August 12, 2019Bad DB design (1)CustomersWe
- 5. Monday, August 12, 2019Bad DB design (2)Insertion
- 6. Monday, August 12, 2019NormalizationNormalization is a step
- 7. Monday, August 12, 2019Compound domains and
- 8. Monday, August 12, 2019Functional dependencies (FD)Let’s relation
- 9. Monday, August 12, 2019KeysSet of attributes K
- 10. Monday, August 12, 2019Properties of functional dependenciesProperties
- 11. Monday, August 12, 2019Logical inference of functional
- 12. Monday, August 12, 2019Closure, completeness, equivalence
- 13. Monday, August 12, 2019FD и сущности предметной
- 14. Monday, August 12, 2019Not full (partial) functional
- 15. Monday, August 12, 2019Anomalies of insertion, deleting
- 16. Monday, August 12, 2019The second normal form
- 17. Monday, August 12, 2019Example of reduction to the 2NFCUSTOMER-PURCHASECUSTOMERPURCHASE
- 18. Monday, August 12, 2019Example of reduction to
- 19. Monday, August 12, 2019Transitive dependencies and
- 20. Monday, August 12, 2019Anomalies of insertion, deleting
- 21. Monday, August 12, 2019The Third Normal Form
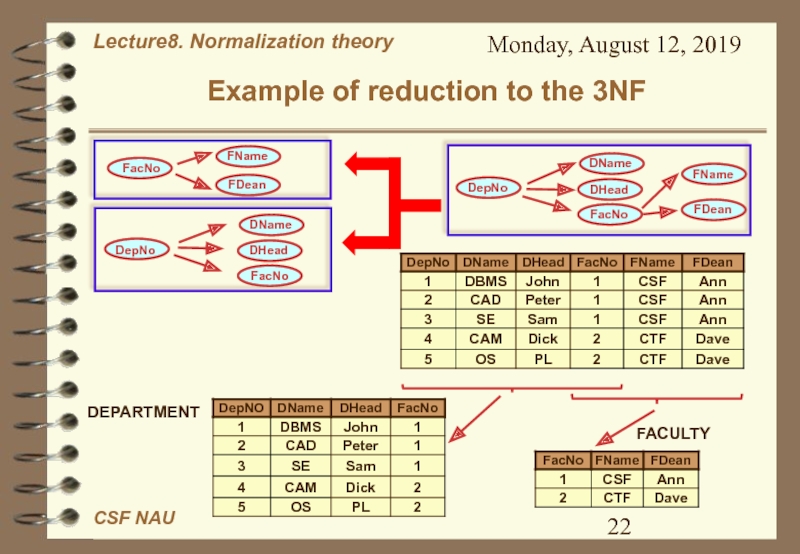
- 22. Monday, August 12, 2019Example of reduction to the 3NF DEPARTMENTFACULTY
- 23. Monday, August 12, 2019Example of reduction to
- 24. Monday, August 12, 2019Strong 3NF (S3NF) Note
- 25. Monday, August 12, 2019Reduction to the S3NF
- 26. Monday, August 12, 2019Boyce-Codd normal form (BCNF)Relation
- 27. Monday, August 12, 2019Multivalued dependencies and
- 28. Monday, August 12, 2019Definition of the multivalued
- 29. Monday, August 12, 2019MVD axiomsGiven relation R
- 30. Monday, August 12, 2019Axioms that relates FD
- 31. Monday, August 12, 2019Some additional properties of
- 32. Monday, August 12, 2019The fourth nornal form
- 33. Monday, August 12, 2019Reduction to the 4NF
- 34. Monday, August 12, 2019Join dependency (JD) and
- 35. Monday, August 12, 2019Relationships between JD and
- 36. Monday, August 12, 2019The Fifth Normal Form
- 37. Monday, August 12, 2019Example of the relation
- 38. Monday, August 12, 2019Example of the relation
- 39. Monday, August 12, 2019Example of the relation
- 40. Monday, August 12, 2019Design of relational model
- 41. Monday, August 12, 2019Formal definition of the
- 42. Monday, August 12, 2019Decomposition of the relational
- 43. Monday, August 12, 2019Equivalence of relational schemas
- 44. Monday, August 12, 2019Equivalence of relational schemas
- 45. Monday, August 12, 2019Equivalence of the normal
- 46. Monday, August 12, 2019Criteria of the relational
- 47. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Lecture 8. Normalization theory of the relational model
National Aviation University
Computer
Science Faculty
Слайд 2Monday, August 12, 2019
CONTENTS
What is the purpose of the normalization
theory of RM
Bad DB projects
Functional dependencies
Multivalued dependencies
Join dependencies
Normal forms
Design of
relational model schemaСлайд 3Monday, August 12, 2019
What is the purpose of the normalization
theory
The theory of relational model normalization establish :
how initial
relational schema may be transformed into other
relational schema, which equivalent initial one in some sense and
Is better it in any sense.
Thus this theory should answer to the following questions:
What criteria of equivalence of relational schemas exist?;
What criteria of estimation of relational schemas quality exist?
What techniques of equivalent transformations of relational schemas exist?
Слайд 4Monday, August 12, 2019
Bad DB design (1)
Customers
We have set a
limit of 9 purchases. What if a customer has more
than 9 purchases?What to do if purchases are less 9? Set values to NULL? What to do if it is necessary to delete purchase in the middle of the list?
What we have to do if it is necessary to order cusomers’ orders.
How does search condition look like? For example to find customer that buy parts with No 2?: (PN1 = 2) OR (PN2 = 2) OR (PN3 = 2) ... OR (PN9 = 2)
9 purchases
Слайд 5Monday, August 12, 2019
Bad DB design (2)
Insertion anomaly: Data cannot
be added because some other data is absent .
Update anomaly:
Data inconsistency or loss of data integrity can arise from data redundancy/repetition and partial update . Deletion anomaly: Data maybe unintentionally lost through the deletion of other data .
Why! It is possible when one relation contains information about two ore more entities of the application domain
CUSTOMER-PURCHASE
Слайд 6Monday, August 12, 2019
Normalization
Normalization is a step by step reversible
process of equivalent transformation of one relational schema into other
that has better characteristics. Every step of such transformation is called normal form.Compound (not atomic) values - 1NF
Not full (partial) functional dependence - 2NF
Transitive functional dependence - 3NF
Multivalued dependence - 4NF
Join dependence - 5NF
There are the following unwanted properties of relations and normal forms that remove corresponding properties:
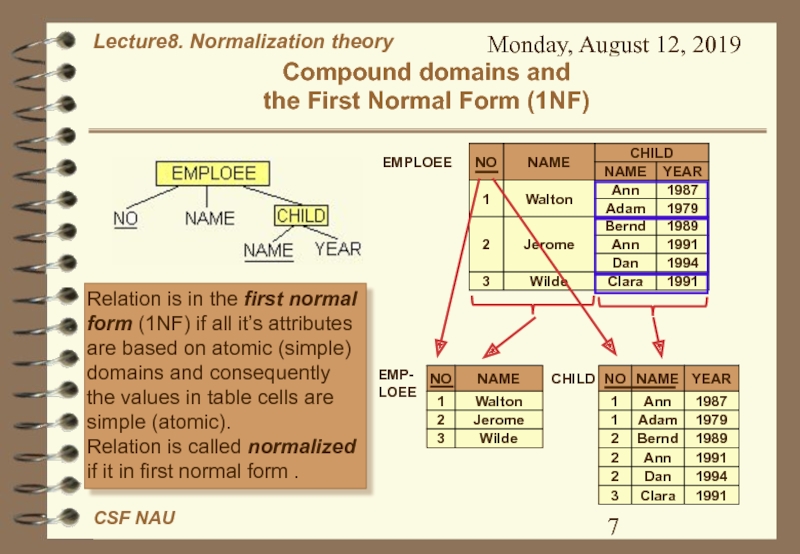
Слайд 7Monday, August 12, 2019
Compound domains and
the First Normal Form
(1NF)
Relation is in the first normal form (1NF) if
all it’s attributes are based on atomic (simple) domains and consequently the values in table cells are simple (atomic). Relation is called normalized if it in first normal form .
Слайд 8Monday, August 12, 2019
Functional dependencies (FD)
Let’s relation R with attributes
A and B is given. In relation R attribute B
functionally depends on attribute A or A functionally determines B, if and only if every value of the projection R[A] is linked exactly to one value of the projection R[B]. Such functional dependence is denoted as R.А → R.В.The set of attributes A is called determinant for the set of attributes B.
Formally FD is defined in such a way :
The presence of FD is property of the relational schema, but not of instance of relational schema, and reflects semantics of the AD.
The set of FD can be viewed as a set of integrity constraints on the relation scheme; it should be preserved under decomposition.
Слайд 9Monday, August 12, 2019
Keys
Set of attributes K in relation R
is candidate key of the relation R if :
each attribute
of the relation R functionally depends on K;any attribute in K cannot be removed from K without violation of property (a).
Assertion: Any relation has candidate key.
Set of attributes K in relation R is called superkey of the relation R if each attribute of the relation R functionally depends on K.
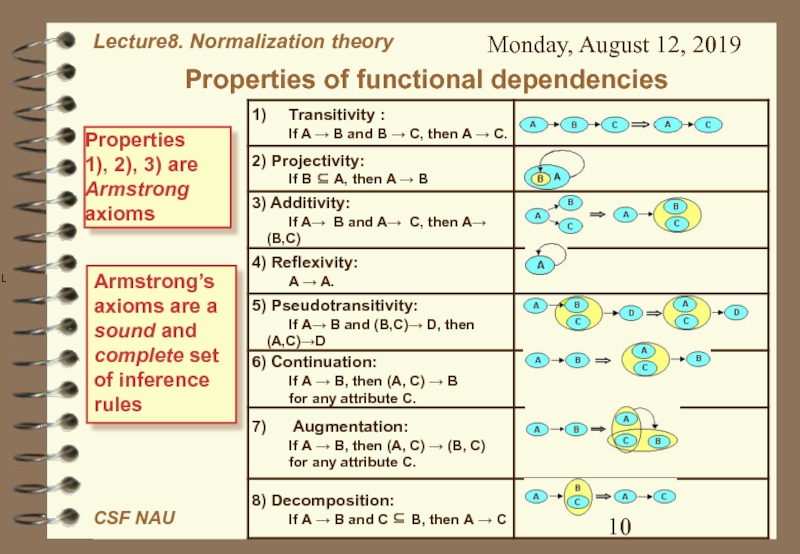
Слайд 10Monday, August 12, 2019
Properties of functional dependencies
Properties
1), 2), 3)
are Armstrong axioms
Armstrong’s axioms are a
sound and complete set of
inference rulesСлайд 11Monday, August 12, 2019
Logical inference of functional dependencies
Let’s R
have set of functional dependencies F and the dependence А
→ С that is not in F. Dependence А → С is logically implied by (or logically deduced from) F if it may be inferred from F with the help of functional dependencies axioms.For example, if we have the relation R(A, B, C) and F contains the dependence А → С, then the following dependences are logically
implied from F:
(А, С) → В - continuation property is applied;
(А, С) → (В, С) - augmentation property is applied .
Слайд 12Monday, August 12, 2019
Closure, completeness, equivalence
and minimal cover of
FD
Let’s relation R have set of functional dependencies F. The
set of all functional dependencies logically implied by F is called (logical) closure of F. It is notified as F+. It is obvious, that F ⊆ F+ и F+ = F++.Set of functional dependencies F is complete if F = F+.
Two sets of dependencies F and G are (logically) equivalent if
F+ = G+.
Lets given sets of functional dependencies F and G such that G ⊂ F. G is a cover of F if G+ =F+. If G is minimal then G is called basis of dependencies of F or minimal cover.
NOTE: Minimal cover isn't necessarily unique.
Слайд 13Monday, August 12, 2019
FD и сущности предметной области
Thesis. If application
domain contains functional dependence А → В there exists class
of the entities that consist of attributes (A, B). More over in this class set of attributes A is an unique identifier of entities of this class (key) and B are properties of these entities .If А → В1, А → В2, …, А → Вn, the exists class of entities with attributes(А, В1,…,Вn), where А – unique identifier and В1,…, Вn – are ordinary attributes.
This thesis gives formal basis for identifying entities in AD.
Слайд 14Monday, August 12, 2019
Not full (partial) functional
dependencies and second normal
form (2NF)
Let’s given relation with schema R(A, B, C). Functional
dependence
R.A → R.B is full if B does not depends functionally from any С ⊂ А
that does not contained in B.CUSTOMER-PURCHASE
Attribute Q-TY depends fully from (PN, CN, DATE)
Attributes NAME and CITY depends fully from CN
Attributes NAME and CITY depends not fully (partially) from (PN, CN, DATE)
Слайд 15Monday, August 12, 2019
Anomalies of insertion, deleting and updating
when
not full FD exist
CUSTOMER-PURCHASE
Update anomalies. When changing customer city it
is necessary to
remember that information about customers may be duplicated.Inset anomalies. When it is necessary to enter information about new customer (Ann) we may do it only when it will do purchase.
Delete anomalies. On deleting information about purchase of Ann we have to delete information about this customer.
Слайд 16Monday, August 12, 2019
The second normal form (2NF)
Relation is
in the second normal form (2NF) if it is in
the first normal form and all its nonprimary attributes are depend fully from candidate key .Теорема (Хита). The relation R with attributes А, В, С , where
R.A → R.B, is equal to natural join of the projections R[A, B] and R[A, C].
Algorithm of reduction to 2NF. Given relation R with set of attributes M. If in R there is not full functional dependence R.A → R.B of non primary attribute B from a candidate key A, the relation R is decomposed into the following two relations: R [A, B] and R [M - B]. If the resulting relations are still not in the second normal form, the mentioned algorithm is applied to these relations again.
Such splitting is called binary decomposition.
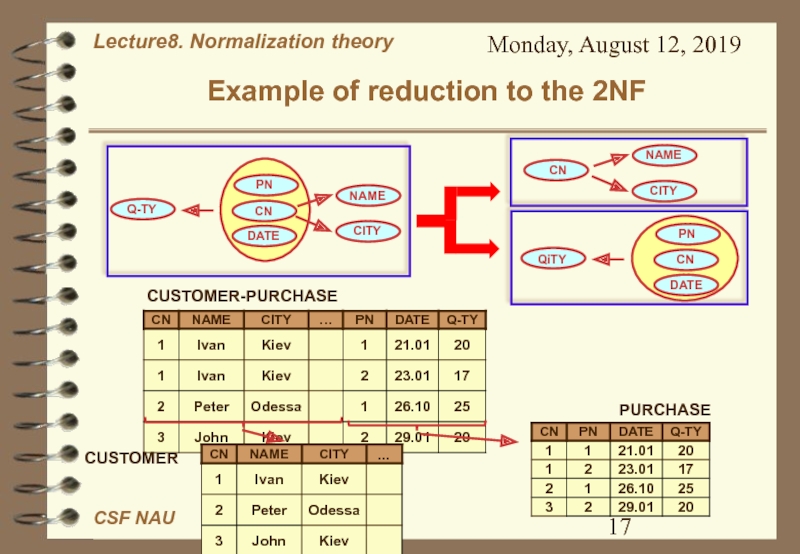
Слайд 18Monday, August 12, 2019
Example of reduction to the 2NF -
Summary
Source relation contains information from 2 entities, every resulting
relations
contain information about one entity each.
Resulting relations do not contain anomalies of deletion, inserting and updating.
Source relation can be restored from resulting relations with the help of natural join.
Such decomposition do not lose functional dependencies. They may be restored from decomposed relations.
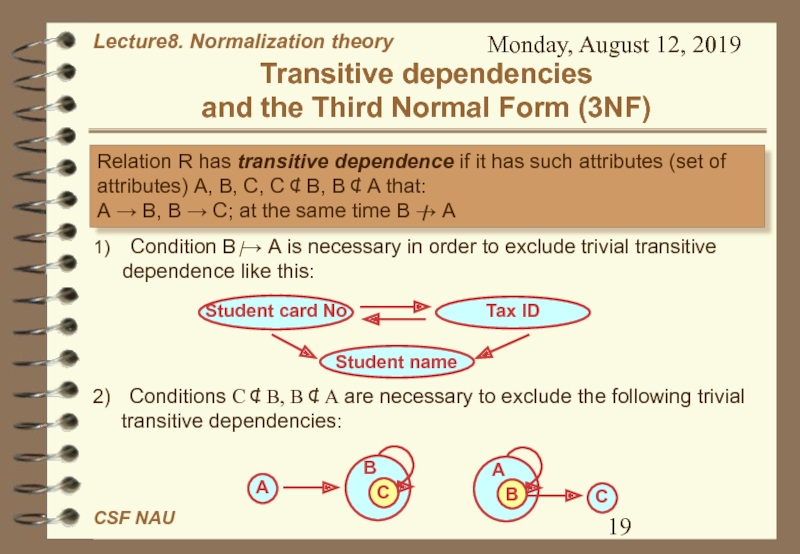
Слайд 19Monday, August 12, 2019
Transitive dependencies
and the Third Normal Form
(3NF)
1) Condition В → А is necessary in order to
exclude trivial transitive dependence like this:Student card No
Tax ID
Student name
2) Conditions С ⊄ В, В ⊄ А are necessary to exclude the following trivial transitive dependencies:
А
С
В
В
А
С
Слайд 20Monday, August 12, 2019
Anomalies of insertion, deleting and updating
when
transitive FD exist
DEPARTMENT-FACULTY
DEPARTMENT entities
FACULTY entities
Availability transitive dependencies in a relation
means the relation
contains information from more that one entity.As a result such relations imply anomalies of insertion, deletion, updating.
Слайд 21Monday, August 12, 2019
The Third Normal Form (3NF)
The relation is
in the third normal form (3NF) if it is in
the second normal form and does not contain transitive dependencies of nonprimary attributes from candidate keys .Other words all nonprimary attributes must functionally depend ONLY from candidate keys.
Algorithm of the relation reduction to 3NF. Let’s given the relation R with attributes A, B, C and there are functional dependencies
R.A → R.B and R.В → R.С. The relation R decomposed into following two relations: R[A, B] and R[B, С]. If the resulting relations are still
not in the third normal form, the mentioned algorithm is applied to
these relations again.
Слайд 23Monday, August 12, 2019
Example of reduction to the 3NF -
Summary
Results the same as in reduction to the 2NF:
Source relation
contains information from 2 entities, every
resulting relations contain information about one entity each.
Resulting relations do not contain anomalies of deletion, inserting and updating.
Source relation can be restored from resulting relations with the help of natural join.
Such decomposition do not lose functional dependencies. They may be restored from decomposed relations.
Слайд 24Monday, August 12, 2019
Strong 3NF (S3NF)
Note that 3NF requires
absence of transitive dependence of nonprimary attributes but not all
attributes of the relation . Strong 3NF requires absence of transitive dependence of ALL attributes of a relationRelation is in strong 3NF, if it is in 3NF and does not contain transitive dependencies of ALL attributes from candidate keys .
This relation is in the 3NF, but still contains information about two entities. So it hold anomalies.
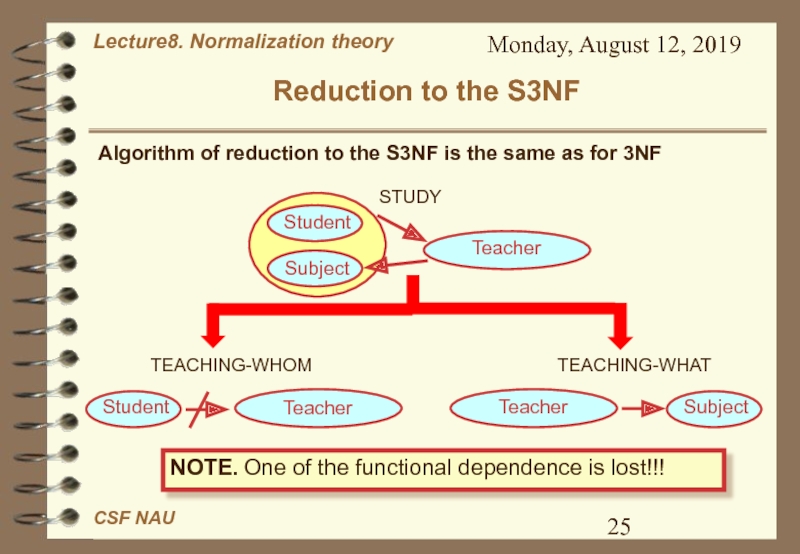
Слайд 25Monday, August 12, 2019
Reduction to the S3NF
Algorithm of reduction
to the S3NF is the same as for 3NF
Student
Subject
Teacher
STUDY
Student
Teacher
Teacher
Subject
TEACHING-WHOM
TEACHING-WHAT
NOTE. One of
the functional dependence is lost!!! Слайд 26Monday, August 12, 2019
Boyce-Codd normal form (BCNF)
Relation R is in
Boyce-Codd normal, if every its determinants is a superkey.
Assertion. S3NF and
BCNF are equivalentСлайд 27Monday, August 12, 2019
Multivalued dependencies and
the Fourth Normal Form
(4NF)
Thesis: If in an application domain there is no
direct relationship between attributes A and B, and it is necessary to fix such relationship in one relation, the only correct decision is to determine, that all values of attribute A are related to all values of attribute B, and vise versa.TEACHING
Слайд 28Monday, August 12, 2019
Definition of the multivalued dependency
(MVD)
Given relation
R with attributes (set of attributes) А, В, С. There
exists multivalued dependency В of А (or А determines В multivalued), denoted as А →→ В, if for given set of values attributes from A there exist set of related values attributes of B and this set of B-values does not depends from values of attributes C.Example: In the relation TEACHING the are the following MVD:
Let’s there is relation R(A,B). The MVDs А →→ ∅ and А →→ В are called trivial because they exist in any relations.
Subject →→ Teacher
Subject →→ Bood
Слайд 29Monday, August 12, 2019
MVD axioms
Given relation R with attributes (set
of attributes) А, В, С.
Multivalued dependences have the following axioms
:1) Complementation axiom
If А →→ В, then А →→ С
2) Augmentation axiom
If А →→ В and V ⊆ W, then (А, W) →→ (В, V)
3) Transitivity axiom
If А →→ В and В →→ С, then А →→ С – В
Слайд 30Monday, August 12, 2019
Axioms that relates FD и MVD
1) Replication axiom
The following two axioms relates functional and multivalued
dependencies .
If
А → В, then А →→ В2) Coalescence axiom
If А →→ В and Z ⊆ B, and for some W,
that is not intersect with B we have W → Z,
then A → Z
Слайд 31Monday, August 12, 2019
Some additional properties of MVD
1) Union
If А
→→ В and А →→ С, then А →→ (В,
С)If А →→ В and (W, В) →→ Z ,
then (W, А) →→ Z – (W, В)
2) Pseudo-transitivity
3) Mixed pseudo-tranisitivity
If А →→ В and (А,В) →→ С, then А →→ (С - В)
4) Intersection and difference
If А →→ В and А →→ С,
then А →→ В ∩ С, А →→ В – С, А →→ С – В
Слайд 32Monday, August 12, 2019
The fourth nornal form (4NF)
The relation R
is in fourth normal form (4NF), if from existence of
nontrivial multivalued dependence X →→ Y (where Y ⊄ Х) it is follows that Х is a superkey of the relation R.Assertion. Lets relation R consists of attributes (set of attributes) А, В, С. Dependence А →→ В exist
in R if and only if R = R[A, B] * R[A, C].
Слайд 33Monday, August 12, 2019
Reduction to the 4NF and embedded MVD
Algorithm
reduction to the 4NF. Lets given relation R with attributes
(set of attributes) А, В, С, and given multivalued dependence R.A →→ R.B. Relation R decomposed into the following two relations: R[A, B] и R[B, С].If resulting relations are not in 4NF the algorithm is applied once more to these relations .
Multivalued dependency is embeded if it is absent in the relation but exists in the projection of the relation by some attributes.
Слайд 34Monday, August 12, 2019
Join dependency (JD) and
the Fifth Normal
Form (5NF)
Lets R is a relation with attributes (set of
attributes) A1, A2,,.., An. Relation R have join dependency with respect of A1, A2,,.., An, that is denoted as *(A1, A2,…, An), if relation R is equal to natural joins of all of its projections over A1, A2,…, An:R = πA1(R)*πA2(R)*... * πAn(R) ⇔ R = R[A1] * R[A2]*…*R[An])
JD is trivial if one of Ai is equal to the list of all attributes of the relation R.
A join dependency is implied by the candidate keys of R if each of Ai (1 ≤ i ≤ n) are superkeys of R.
Слайд 35Monday, August 12, 2019
Relationships between JD and MVD
Every JD of
the form *(A, B) in relation with schema R(A,B), where
А and В - set of attributes, is equivalent to the MVDs А ∩ В →→ А and А ∩ В →→ В. (Any MVD is JD, but not wise versa!!!)But there exist JD that are not equivalent any MVD. An example of such JD in relation R(A, B, C) is the dependency *((A,B), (B, C), (A,C)). It is not equivalent to any MVD. Example:
In the example to the left relation contains JD
*((A,B), (B, C), (A,C)). It may be verified by calculating: πA1(R) * πA2(R) *... * πAn(R) .
But it does not contain any nontrivial MVD.
It may be convinced by testing that no one of the following multi-valued dependency exist:
A →→B, A →→C, B →→A, B →→C, C →→A,C →→B.
Слайд 36Monday, August 12, 2019
The Fifth Normal Form - 5NF
Relation R
is in the fifth normal form (5NF) if and only
if for all of its nontrivial JD *(А1, А2,…, Аn) all sets of attributes Ai are superkeys of R.This normal form is also called project-join normal form (PJNF).
Assertion. Because of any multivalued dependency is also join dependency, any relation in PJNF (5NF) is also in 4NF .
Classic example to motivate 5NF involves a join n-way decomposition
that cannot be derived by a sequence of 2-way decompositions
Слайд 37Monday, August 12, 2019
Example of the relation in the 5NF
Let’s
the is a relation TBS(TCH, BOK, SBJ), where we record
information aboutsuch ssues : what teaches what books are used;
what books in what subjects are used;
what subjects by what teachers are taught.
The fact that the relation contains the following information:
Reznichenko uses in his lectures the book «SQL language»,
The book «SQL language» is used in the subject DB&KB» and
Reznihcenko has lectures by subject DB&KB.
Does not mean that «Reznichenko uses the book ”SQL Language” in his lectures by subject DB&KB»
Relation TBS is in 5NF because it do not have JDs.
Слайд 38Monday, August 12, 2019
Example of the relation that violates 5NF,
and reduction it to the 5NF
If relation TBS has additional
rule (as a business rule of the application domain): then relation TBS has JD *((TCH, BOK), (BOK, SBJ), (TCH, SBJ)) and this relation is not in 5NF because it has the only candidate key that coincide with all attributes of the relation, that is (TCH, BOK, SUBJ).
In this case relation TBS reduces to 5NF in such a way:
«From the facts:
- teacher t uses in his lectures book b,
- book b is used in subject s and
- teacher t has lectures by subject s
follows that teacher t uses book b in lectures by subject s»,
TBS(TCH, BOK, SBJ) ⇒TB(TCH,BOK), BS(BOK, SBJ), TS(TCH, SBJ)
Слайд 39Monday, August 12, 2019
Example of the relation that violates 4NF,
and reduction it to the 4NF
If relation TBS has additional
rule (as a business rule of the application domain):Then relation TBS has JD *((TCH, BOK), (TCH, SBJ)) or it is the same
as the relation has the following MVDs TCH →→ BOK, TCH →→ SBJ, and this relation neither in 5NF nor in 4NF.
In this case TBS reduces to the 4NF (and more over to the 5NF) in such a way:
«From the facts:
- teacher t uses in his lectures book b,
- teacher t has lectures by subject s
follows that teacher t uses book b in lectures by subject s»,
TBS(TCH, BOK, SBJ) ⇒TB(TCH,BOK), TS(TCH, SBJ)
Слайд 40Monday, August 12, 2019
Design of relational model schema
Formal description of
the relational schema design task
Decomposition of the relational schema
Equivalence
of relationsLoosless decomposition with data preservation
Loosless decomposition with dependencies preservation
Equivalence of the normal forms
Criteria of a relation qualities
Слайд 41Monday, August 12, 2019
Formal definition of the relational schema
design
task
In this definition it is necessary to clarify the following
items:what procedure must be used to convert one set of relations into another;
what does equivalence of the two schemas mean ;
how can we estimate that one relational schema is better than another .
Thesis of universal relation. All application domain may be represented as one universal relation that contains all attributes of the domain.
Formal definition of the design task. Lets given relational schema S0, that contains schema of the only (universal) relation R:
S0 = {R =
SD = {Ri =
that should be better in any sense that schema S0.
Слайд 42Monday, August 12, 2019
Decomposition of the relational schema
It is said
that decomposition has the property of looseless join, if R
is a natural join of the relations R1, R2,…, Rn., that is R = R1 * R2 *…* RnDecomposition is the only operation that is used while splitting relational schemas
Decomposition relation R(M) with set of attributes M into the set of relations R1, R2,…, Rn with attributes M1, MA2,…, Mn is a procedure that satisfy the following conditions:
М1 ∪ М2 ∪ … ∪ Мn = М. That is any attribute of R belongs at
least one of relation Ri and all attributes of Ri should be defined
in R .
All relations Ri, i = 1, 2,..., n, are projections of the relation R over
attributes that are contained in the Ri, that is
Ri(Mi) = πMi(R)
Слайд 43Monday, August 12, 2019
Equivalence of relational schemas
by dependencies
Equivalence by
dependencies. Two sets of the relations are equivalent by dependencies,
if they defined on the same set of attributes and they have the same set of dependencies (functional and multivalued).Formally, lets given two schemas S0 and SD, that was defined previously. They are equivalent by dependencies if:
Where U, Ui are attributes of the schemas S0 and SD: and G, Gi are dependencies of S0 and SD.
Слайд 44Monday, August 12, 2019
Equivalence of relational schemas
by data
Equivalence by
data. Two sets of relations equivalent by data if natural
join of both set of relations gives the identical relations.If source and resulting schemas are S0 and SD, equivalence by data means that splitting of the relation is done by using loosless decomposition.
How does loosless decomposition may be achived?
Assretion. If R1(U1) R2(U2) are decomposition of R(U)
that preserve functional and/or multivalued dependencies, then this decomposition provides lossless join if and only if:
U1 ∩ U2 → (or →→) U1 – U2
OR
U1 ∩ U2 → (or →→) U2 – U1
Слайд 45Monday, August 12, 2019
Equivalence of the normal forms
Property of loosless
join not always guarantee dependency preservation.
At the same time
relation splitting that provides dependency preservation not always guantee the property of loosless join.Equivalence of the normal forms.
Decomposition of the universal relation up to the 3NF preserve equivalence by data and dependencies.
Converting universal relation to the BCNF preserve equivalence by data but not preserve equivalence by dependencies.
Слайд 46Monday, August 12, 2019
Criteria of the relational schema quality
Let
us consider how can we estimate the schema quality: that
is criteria that one schema is better than other.One schema is better that other if it does not have data manipulation anomalies .
Actually quality of the schema may be estimated by normal forms. The higher form is used the more qualified schema is received .