Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы первого порядка
Содержание
- 1. Методы первого порядка
- 2. 08/13/2019Общая характеристика методов первого порядкаЧем больше
- 3. 08/13/2019Как известно, направление градиента является направлением наискорейшего
- 4. 08/13/2019Метод тяжелого шарикаПредставим себе котлован. Мы находимся
- 5. 08/13/2019Уравнение траектории тяжелого шарика- скорость движения шарика-
- 6. 08/13/2019Решение уравненияЗадаем две точки Вычисляем градиентПодставляем в
- 7. 08/13/2019Вычисление градиентаЕсли функция задана аналитически, напримерТо просто пишем подпрограммуProcedure gradF(var x,dF:mas;n:byte);Begin df[1]:=6*x[1]; df[2]:=-2*x[2];End;
- 8. 08/13/2019Вычисление градиентаЕсли функция задана в виде сложной
- 9. 08/13/2019РезюмеЕсли правильно подобрать управляющие параметры a, b,
- 10. 08/13/2019Общий алгоритм метода спуска по градиенту1. Задается
- 11. 08/13/2019Общий алгоритм метода спуска по градиенту4. С
- 12. 08/13/2019Общий алгоритм метода спуска по градиенту6 Проверим
- 13. 08/13/2019x1x2В случае длинного оврага, если начальная точка
- 14. 08/13/2019Программная реализацияType fun=function (x:mas):realProcedure MPSP(F:fun; var x0:mas;eps,h:real;var fm:real);Procedure gradF(var x,dF:mas,n:byte,h:real);Begindf[1]:=(F(x[1]+h,x[2])-F(x[1]-h,x[2]))/(2*h); df[2]:=(F(x[1],x[2]+h)-F(x[1],x[2]-h))/(2*h);End;Var d:mas;
- 15. 08/13/2019Подпрограмма для функции ϕ(z) вдоль направления
- 16. 08/13/2019Реализация алгоритма спуска к минимумуBegin repeat gradF(x0,dF,n);
- 17. 08/13/2019Метод сопряженных направленийДва направления
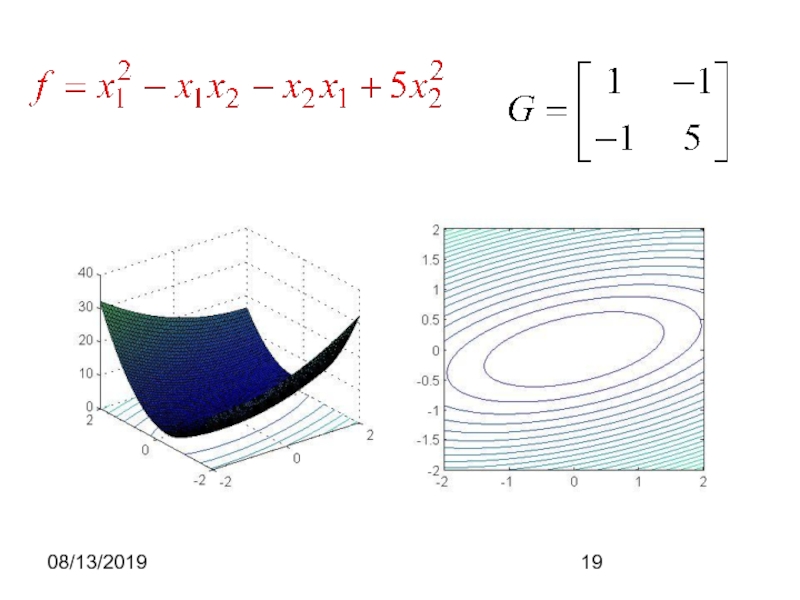
- 18. 08/13/2019Квадратичная функцияЕе матрица симметричнаЕсли матрица положительно определеннаяТогда квадратичная функция имеет минимум
- 19. 08/13/2019
- 20. 08/13/2019Сопряженные направленияd1d2Для квадратичной функции n – переменных
- 21. 08/13/2019Метод параллельных прямыхd1d2В заданной точке х0 выбираем
- 22. 08/13/2019Метод Флетчера-Ривса
- 23. 08/13/2019Алгоритм метода Флетчера-Ривса1. Задается начальная точка
- 24. 08/13/2019Конец
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 108/13/2019
Тема 3 Методы оптимизации первого порядка
Метод тяжелого шарика
Метод спуска по
градиенту
Слайд 208/13/2019
Общая характеристика
методов первого порядка
Чем больше информации о функции известно,
тем более эффективно можно достичь минимума, если этой информацией правильно
распорядитьсяМетоды нулевого порядка фактически не располагают никакой информацией о функции (это черный ящик). Правда в процессе спуска они ее накапливают и используют для очередного спуска (например метод Розенброка осуществляет поворот координат в зависимости от результатов предыдущего спуска)
В методах первого порядка при выборе следующего направления спуска используется градиент функции в текущей точке и в предыдущей
Слайд 308/13/2019
Как известно, направление градиента является направлением наискорейшего возрастания функции в
данной точке. Следовательно, противоположное направление является направлением наискорейшего убывания функции.
Это свойство в основном и используется для построения методов минимизации первого порядка.При этом направление наискорейшего убывания в данной точке не всегда оказывается наилучшим для спуска к минимуму.
Поэтому для повышения эффективности вводят различные поправки.
При выборе очередного направления используют накопленную информацию о функции из предыдущих спусков.
Множество возможностей введения таких поправок определяет многообразие различных методов первого порядка.
Слайд 408/13/2019
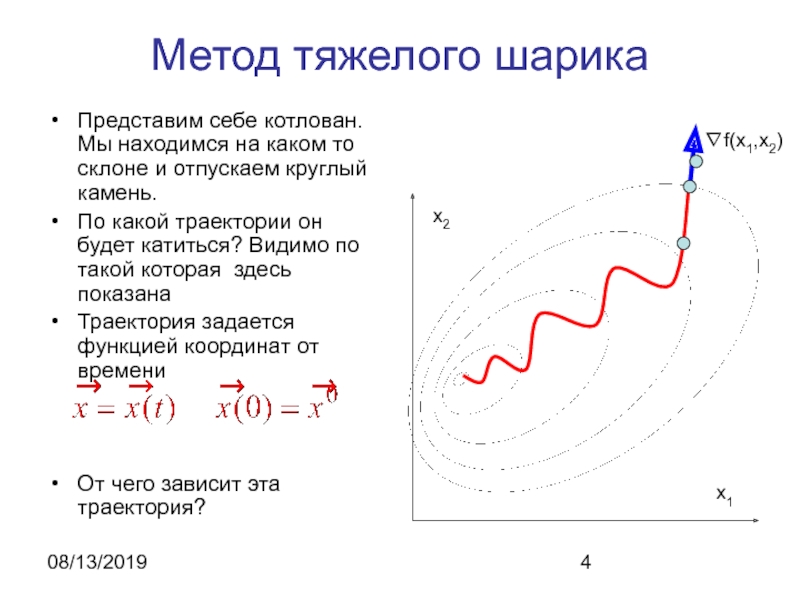
Метод тяжелого шарика
Представим себе котлован. Мы находимся на каком то
склоне и отпускаем круглый камень.
По какой траектории он будет
катиться? Видимо по такой которая здесь показанаТраектория задается функцией координат от времени
От чего зависит эта траектория?
∇f(x1,x2)
x1
x2
Слайд 508/13/2019
Уравнение траектории тяжелого шарика
- скорость движения шарика
- ускорение шарика
- сила
тяжести шарика
- сила трения шарика
уравнение движения шарика
Слайд 608/13/2019
Решение уравнения
Задаем две точки
Вычисляем градиент
Подставляем в уравнение и получаем
новую точку
Подставляем
получаем и т.д.Можно использовать разные методы решения этой задачи Коши
Мы используем то, что вам уже знакомо
Слайд 708/13/2019
Вычисление градиента
Если функция задана аналитически, например
То просто пишем подпрограмму
Procedure gradF(var
x,dF:mas;n:byte);
Begin
df[1]:=6*x[1];
df[2]:=-2*x[2];
End;
Слайд 808/13/2019
Вычисление градиента
Если функция задана в виде сложной программы, и производные
невозможно просто вычислить
Function F(var x:mas,n:byte):real;
Begin
f:=sqr(x[1]-x[2])+2*sqr(x[1])
End;
То пишем подпрограмму
Procedure gradF(var
x,dF:mas,n:byte,h:real);Begin
df[1]:=(F(x[1]+h,x[2])-F(x[1]-h,x[2]))/(2*h);
df[2]:=(F(x[1],x[2]+h)-F(x[1],x[2]-h))/(2*h);
End;
Слайд 908/13/2019
Резюме
Если правильно подобрать управляющие параметры a, b, τ и метод
решения задачи Коши то метод шарика может конкурировать с методами
нулевого порядка. Однако на настройку параметров уходит довольно много времени.Метод тяжелого шарика имеет лишь методическое значение, в силу больших затрат на настройку и реализацию алгоритма
Однако он показывает, как можно систематически спускаться к минимуму если знать градиент функции
Более эффективны методы спуска, в которых очередное направление выбирается с использованием градиента
Ниже мы рассмотрим общий алгоритм таких методов
Слайд 1008/13/2019
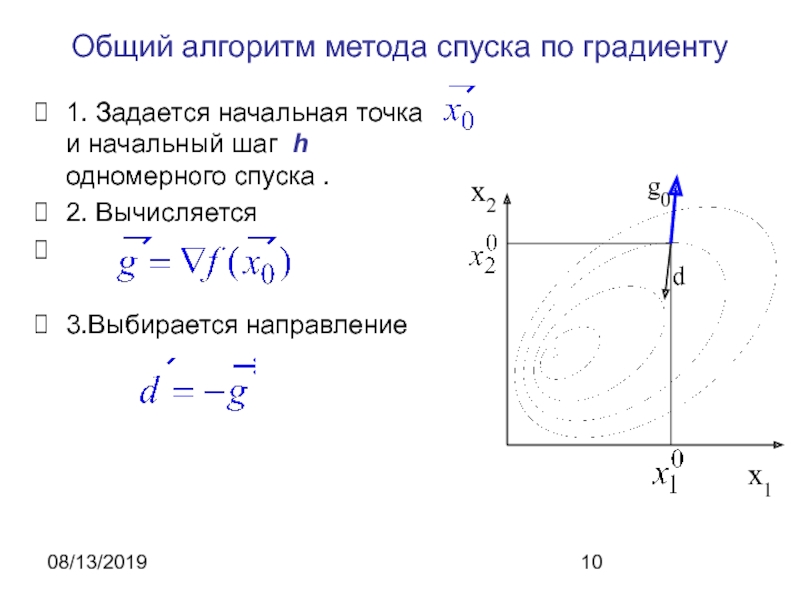
Общий алгоритм метода спуска по градиенту
1. Задается начальная точка
и начальный шаг h одномерного спуска .
2.
Вычисляется 3.Выбирается направление
x1
x2
d
g0
Слайд 1108/13/2019
Общий алгоритм метода спуска по градиенту
4. С помощью метода Мpp
найти zm доставляющее
5. Перейти в новую точку
x1
x2
d
g0
zm
Слайд 1208/13/2019
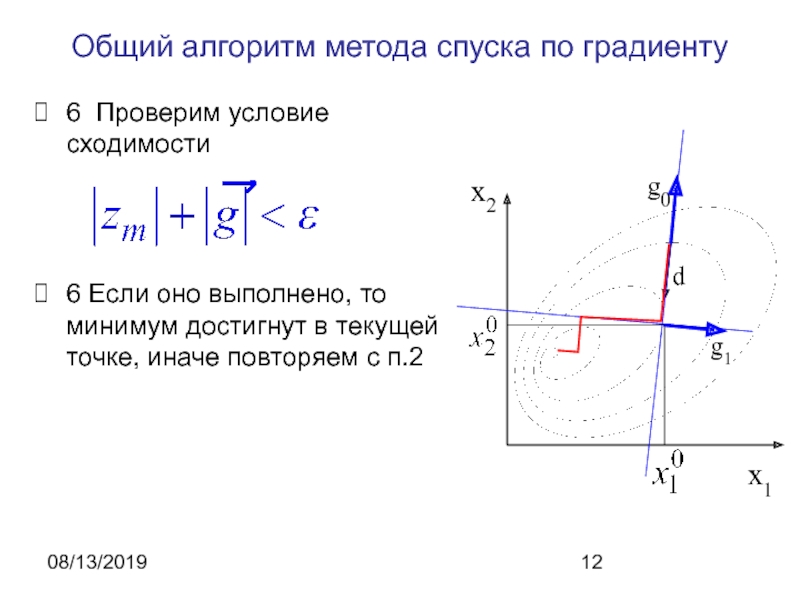
Общий алгоритм метода спуска по градиенту
6 Проверим условие сходимости
6 Если
оно выполнено, то минимум достигнут в текущей точке, иначе повторяем
с п.2x1
x2
d
g0
g1
Слайд 1308/13/2019
x1
x2
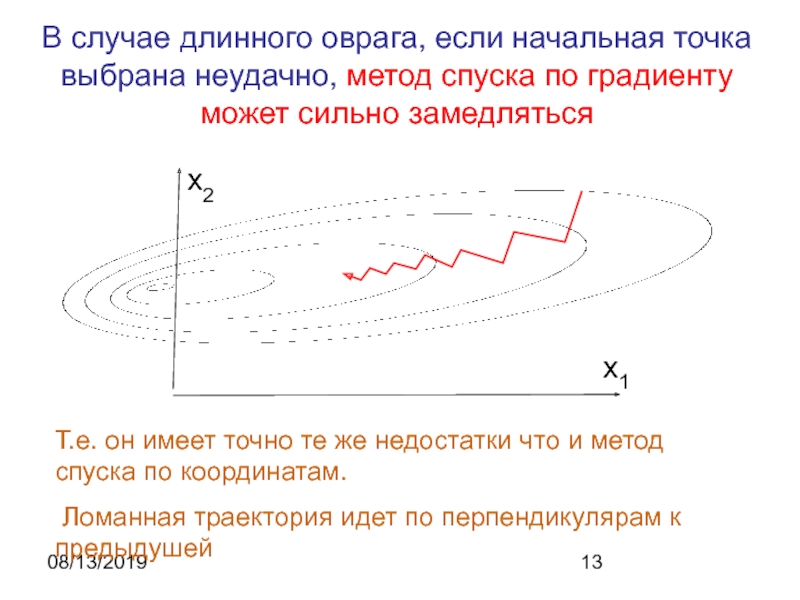
В случае длинного оврага, если начальная точка выбрана неудачно, метод
спуска по градиенту может сильно замедляться
Т.е. он имеет точно те
же недостатки что и метод спуска по координатам.Ломанная траектория идет по перпендикулярам к предыдушей
Слайд 1408/13/2019
Программная реализация
Type fun=function (x:mas):real
Procedure MPSP(F:fun;
var x0:mas;eps,h:real;var fm:real);
Procedure gradF(var
x,dF:mas,n:byte,h:real);
Begin
df[1]:=(F(x[1]+h,x[2])-F(x[1]-h,x[2]))/(2*h);
df[2]:=(F(x[1],x[2]+h)-F(x[1],x[2]-h))/(2*h);
End;
Var d:mas;
Слайд 1508/13/2019
Подпрограмма для функции ϕ(z)
вдоль направления
function F1(z:
real): real;
begin
for k:=1 to n do
x[k]=x0[k]+z*D[k];
F1:=F(x);
end;
Слайд 1608/13/2019
Реализация алгоритма спуска к минимуму
Begin
repeat
gradF(x0,dF,n);
for i:=1 to
n do D[i]:=-dF[i];
zm:=MPP(0,h,h/5);
x0:=x;
dl:=zm;
for i:=1 to n
dodl:=dl+abs(dF[i]);
end;
Until dl
End;
Слайд 1708/13/2019
Метод сопряженных направлений
Два направления и
называются сопряженными относительно симметричной, положительно определенной матрицы
G еслиИзвестно, что для квадратичной функции можно построить n взаимно сопряженных направлений, спуск по которым приведет к точке минимума ровно за n шагов.
На этом свойстве основана большая группа методов - сопряженных градиентов, сопряженных направлений, параллельных касательных и др.
Слайд 1808/13/2019
Квадратичная функция
Ее матрица симметрична
Если матрица положительно определенная
Тогда квадратичная функция имеет
минимум
Слайд 2008/13/2019
Сопряженные направления
d1
d2
Для квадратичной функции n – переменных с положительно определенной
матрицей G в каждой точке x0 можно построить набор n
сопряженных (относительно ее матрицы) векторов, последовательный спуск по которым приведет точно в минимумВопрос в том, как их построить, если не знать G
Слайд 2108/13/2019
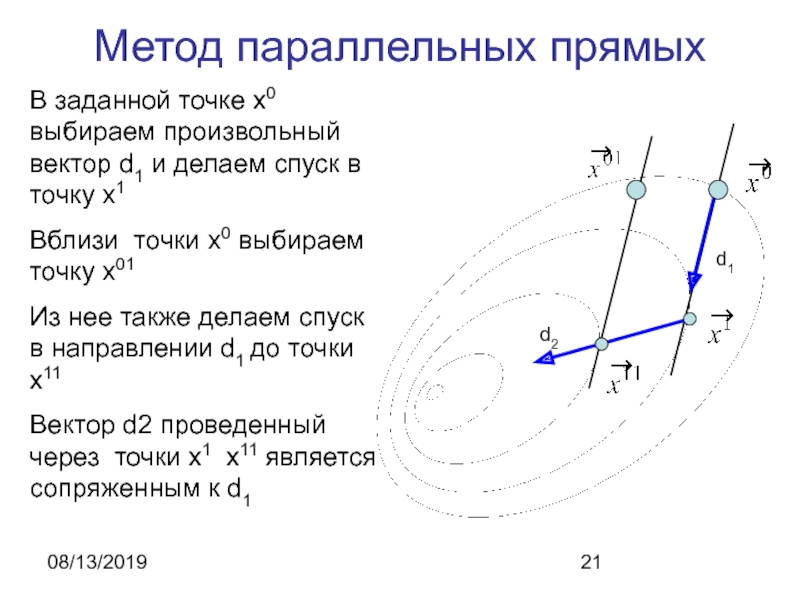
Метод параллельных прямых
d1
d2
В заданной точке х0 выбираем произвольный вектор d1
и делаем спуск в точку х1
Вблизи точки х0 выбираем точку
х01Из нее также делаем спуск в направлении d1 до точки х11
Вектор d2 проведенный через точки х1 х11 является сопряженным к d1
Слайд 2308/13/2019
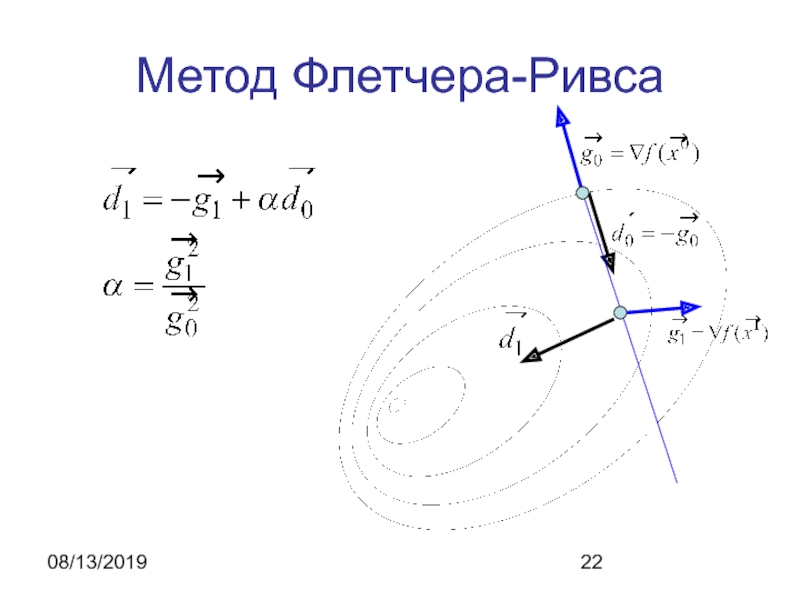
Алгоритм метода Флетчера-Ривса
1. Задается начальная точка
и начальный шаг h одномерного спуска , вычисляется.
Повторяем n раз:
2.
Делаем спуск zm3. Переходим в новую точку
4. Вычисляем
5. Выбирается направление
6. Пересылаем
Конец повтора
Если zm<ε повторим с п.1





![Методы первого порядка 08/13/2019Вычисление градиентаЕсли функция задана аналитически, напримерТо просто пишем подпрограммуProcedure gradF(var x,dF:mas;n:byte);Begin df[1]:=6*x[1]; df[2]:=-2*x[2];End; 08/13/2019Вычисление градиентаЕсли функция задана аналитически, напримерТо просто пишем подпрограммуProcedure gradF(var x,dF:mas;n:byte);Begin df[1]:=6*x[1]; df[2]:=-2*x[2];End;](/img/thumbs/35f4a67cdc5193f09e55d67e092e3ebd-800x.jpg)
![Методы первого порядка 08/13/2019Вычисление градиентаЕсли функция задана в виде сложной программы, и производные невозможно 08/13/2019Вычисление градиентаЕсли функция задана в виде сложной программы, и производные невозможно просто вычислить Function F(var x:mas,n:byte):real;Begin f:=sqr(x[1]-x[2])+2*sqr(x[1])End;То](/img/thumbs/32590b04477cd0645c9110e7a3b515a2-800x.jpg)


![Методы первого порядка 08/13/2019Программная реализацияType fun=function (x:mas):realProcedure MPSP(F:fun; var x0:mas;eps,h:real;var fm:real);Procedure gradF(var x,dF:mas,n:byte,h:real);Begindf[1]:=(F(x[1]+h,x[2])-F(x[1]-h,x[2]))/(2*h); df[2]:=(F(x[1],x[2]+h)-F(x[1],x[2]-h))/(2*h);End;Var d:mas; 08/13/2019Программная реализацияType fun=function (x:mas):realProcedure MPSP(F:fun; var x0:mas;eps,h:real;var fm:real);Procedure gradF(var x,dF:mas,n:byte,h:real);Begindf[1]:=(F(x[1]+h,x[2])-F(x[1]-h,x[2]))/(2*h); df[2]:=(F(x[1],x[2]+h)-F(x[1],x[2]-h))/(2*h);End;Var d:mas;](/img/thumbs/5795ae12a2b0354cb5eeae80c7dcf29b-800x.jpg)
![Методы первого порядка 08/13/2019Подпрограмма для функции ϕ(z) вдоль направления function F1(z: real): real; begin for k:=1 to n do x[k]=x0[k]+z*D[k]; F1:=F(x); end; 08/13/2019Подпрограмма для функции ϕ(z) вдоль направления function F1(z: real): real; begin for k:=1 to n do x[k]=x0[k]+z*D[k]; F1:=F(x); end;](/img/thumbs/40b40a024431570bb2ae49e67332f06c-800x.jpg)
![Методы первого порядка 08/13/2019Реализация алгоритма спуска к минимумуBegin repeat gradF(x0,dF,n); for i:=1 to n 08/13/2019Реализация алгоритма спуска к минимумуBegin repeat gradF(x0,dF,n); for i:=1 to n do D[i]:=-dF[i]; zm:=MPP(0,h,h/5); x0:=x; dl:=zm; for](/img/thumbs/402c5d7d73d8ac74be24b9c074414042-800x.jpg)