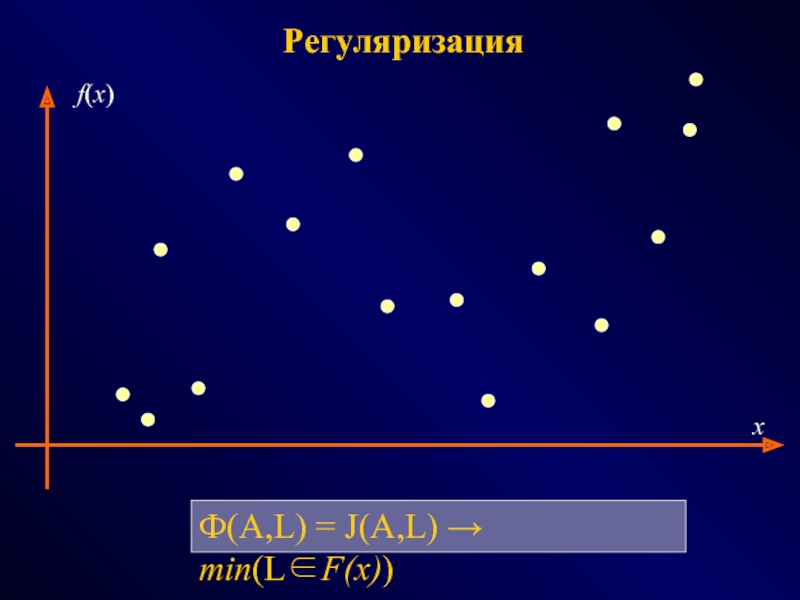
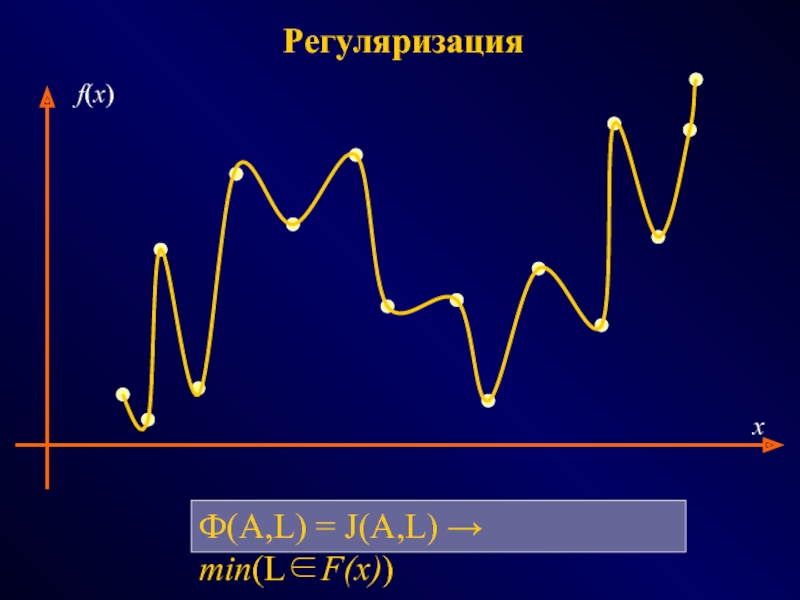
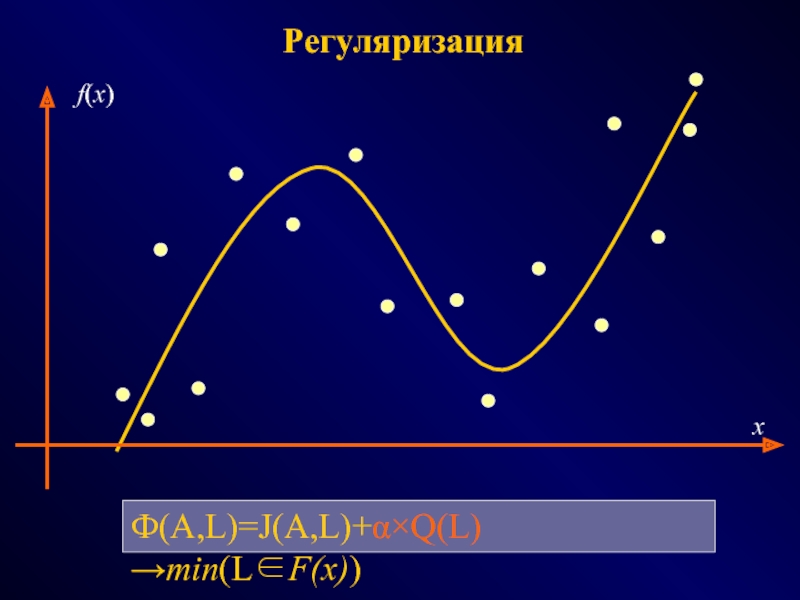
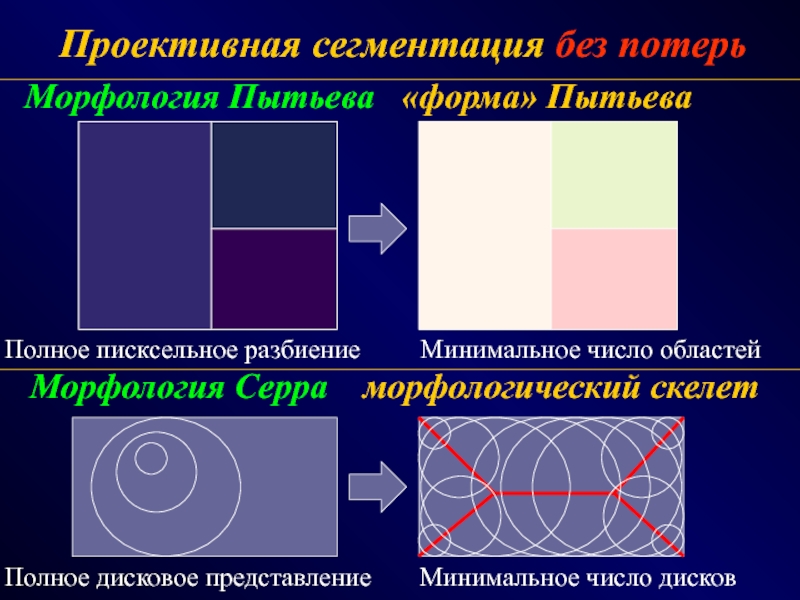
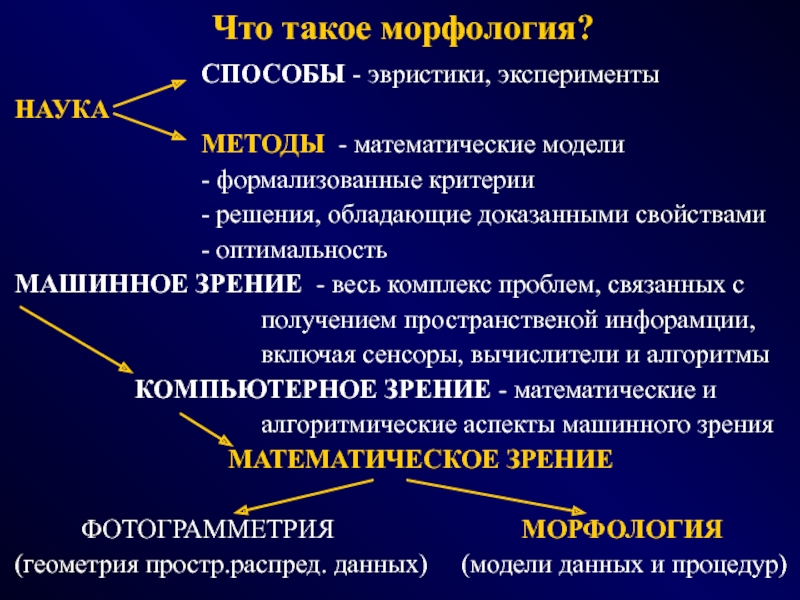
СПОСОБЫ - эвристики, эксперименты
НАУКА
МЕТОДЫ - математические модели
- формализованные критерии
- решения, обладающие доказанными свойствами
- оптимальность
МАШИННОЕ ЗРЕНИЕ - весь комплекс проблем, связанных с
получением пространственой инфорамции,
включая сенсоры, вычислители и алгоритмы
КОМПЬЮТЕРНОЕ ЗРЕНИЕ - математические и
алгоритмические аспекты машинного зрения
МАТЕМАТИЧЕСКОЕ ЗРЕНИЕ
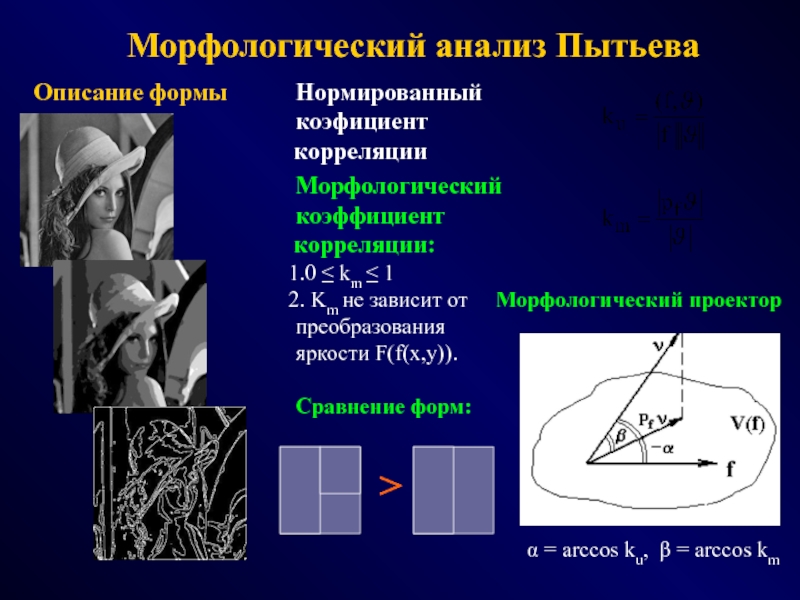
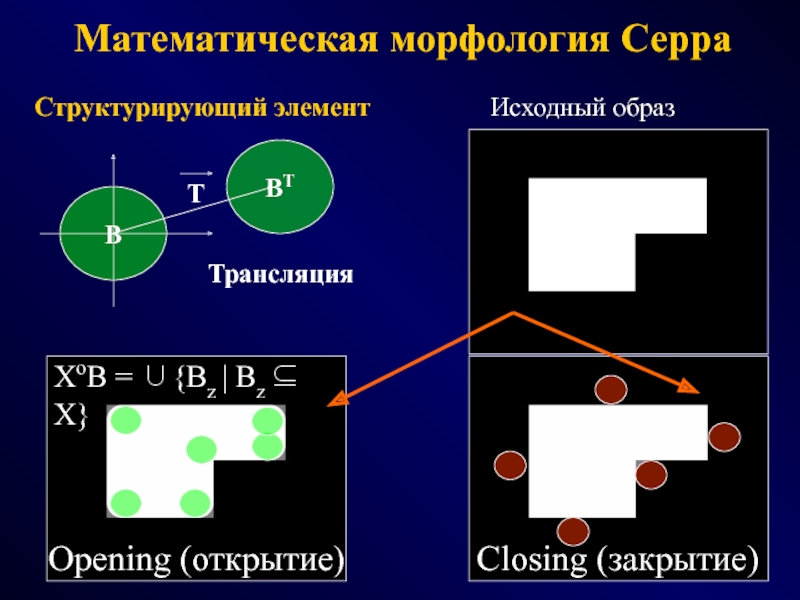
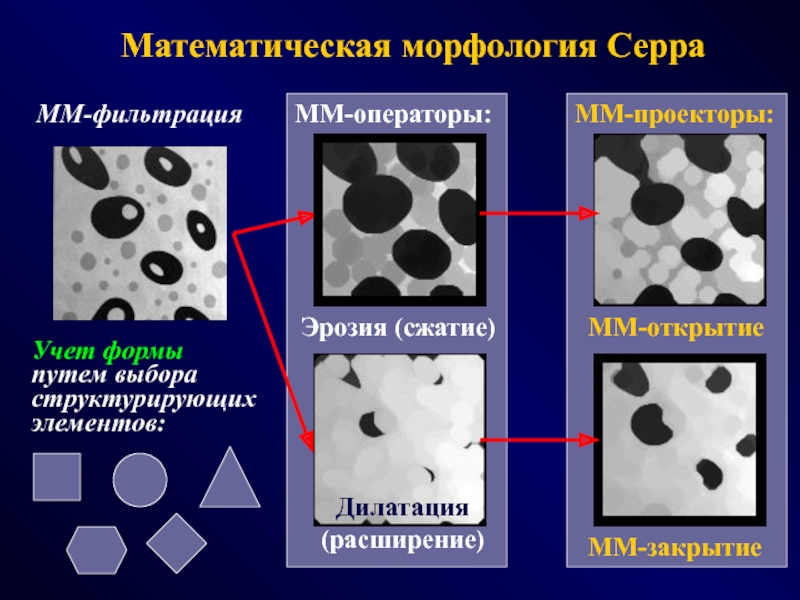
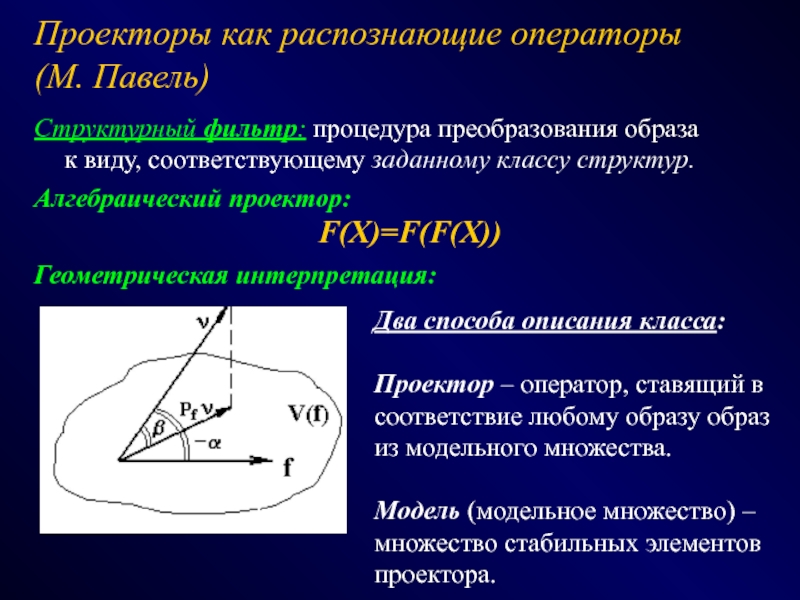
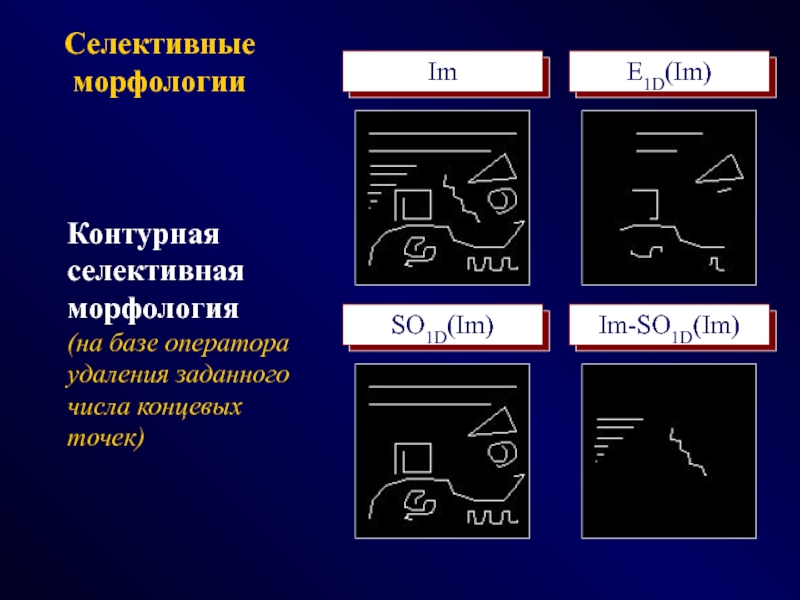
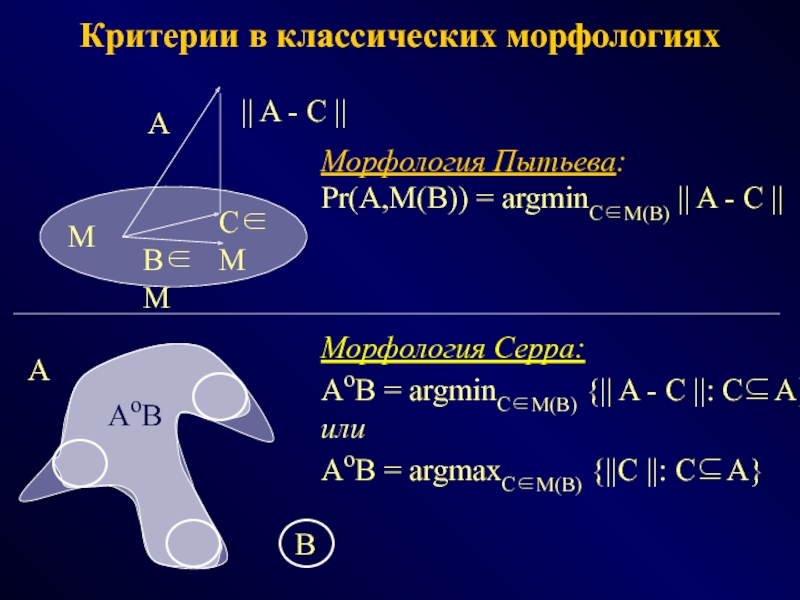
ФОТОГРАММЕТРИЯ МОРФОЛОГИЯ
(геометрия простр.распред. данных) (модели данных и процедур)


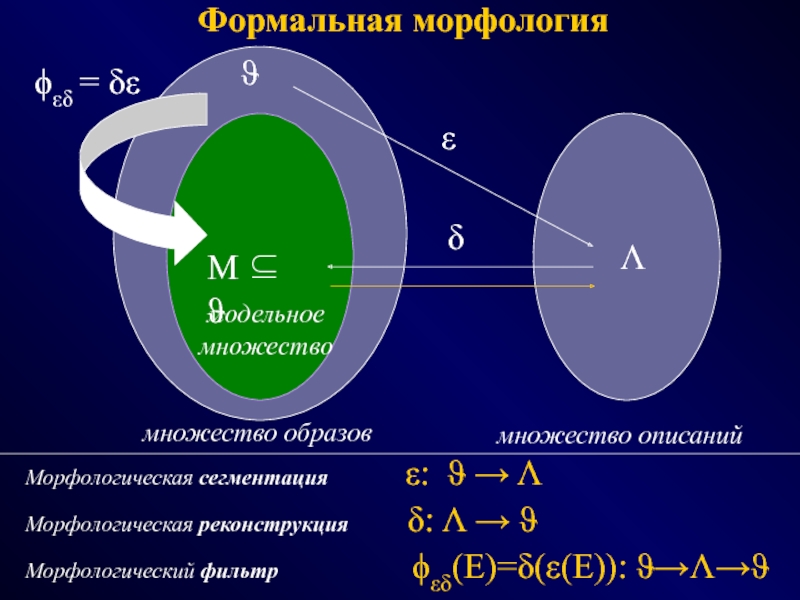




















![МОРФОЛОГИЧЕСКИЕ СИСТЕМЫ и АНАЛИЗ ИЗОБРАЖЕНИЙ Критериальная морфология:Модель: M(λ): Λ→[0,1] ⇔ M(L):ϑ→[0,1]Критерий соответствия:K(E,λ): ϑ×Λ→[0,1] ⇔ K(E,L): ϑ×ϑ→[0,1]Критериальный Критериальная морфология:Модель: M(λ): Λ→[0,1] ⇔ M(L):ϑ→[0,1]Критерий соответствия:K(E,λ): ϑ×Λ→[0,1] ⇔ K(E,L): ϑ×ϑ→[0,1]Критериальный морфологический фильтр ϕФ на базе (ε,δ):εФ(E)=λ,](/img/thumbs/e058b9206da4bc77c3a1e271e1db237a-800x.jpg)

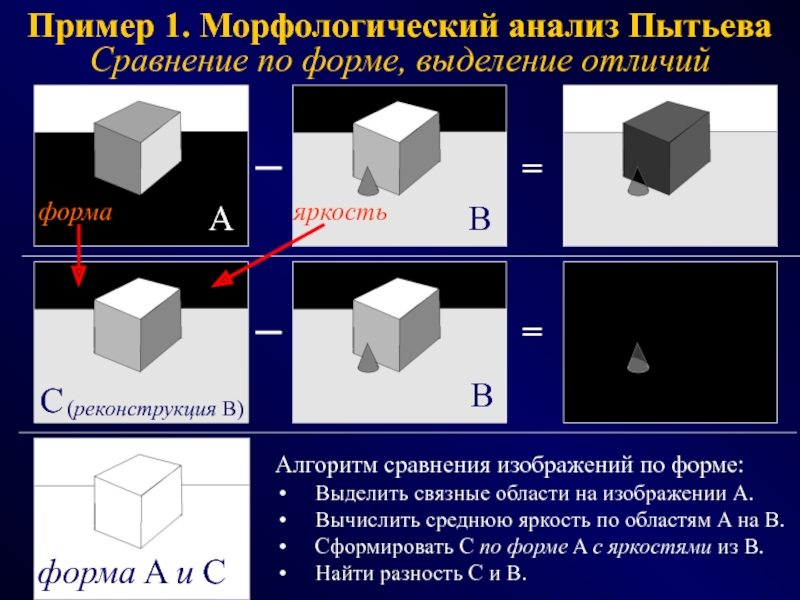
![МОРФОЛОГИЧЕСКИЕ СИСТЕМЫ и АНАЛИЗ ИЗОБРАЖЕНИЙ Нечеткие модели: [0,1]Максимум достоверности:Ф(A,L)=K(A,L)×M(L)→max(L∈Ω)Вероятностные модели: [0,1]Максимум апостериорной вероятностиψ(A)=L: P(A,L)=P(A/L)×P(L)→max(L∈Ω).Четкие или логические Нечеткие модели: [0,1]Максимум достоверности:Ф(A,L)=K(A,L)×M(L)→max(L∈Ω)Вероятностные модели: [0,1]Максимум апостериорной вероятностиψ(A)=L: P(A,L)=P(A/L)×P(L)→max(L∈Ω).Четкие или логические модели: [0,1] → {0,1}.Морфологическая проекция на](/img/thumbs/daafb6a6bdd1555df8800804ac596bbe-800x.jpg)