Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физика конденсаторного состояния
Содержание
- 1. Физика конденсаторного состояния
- 2. кристаллыаморфные твердые телажидкие кристаллытвердые теланеупорядоченные сплавыквантовые жидкостиквантовые
- 3. A. Классификация связей частицМОЛЕКУЛЯРНЫЕКОВАЛЕНТНЫЕМЕТАЛЛИЧЕСКИЕ ИОННЫЕ ТИПЫ КОНДЕНСИРОВАННЫХ
- 4. ArKClCKБ. Виды конденсированных тел по типу распределения
- 5. Слайд 5
- 6. Параметры конденсированных тел Параметр взаимодействия Параметр де Бройля
- 7. а – межатомное расстояние; m – масса
- 8. КВАНТОВАЯ СТАТИСТИКА Статистическое описание систем многих частицПусть
- 9. Квантовая статистикаВ системе многих квантовых частиц возникают
- 10. Квантовая статистика Ферми-ДиракаВ каждом энергетическом состоянии –
- 11. Квантовая статистика Бозе-ЭйнштейнаБозе-газ – газ частиц с
- 12. Электроны – фермионы – полуцелый спин =>
- 13. А. Полная энергия электронного газа при нулевой
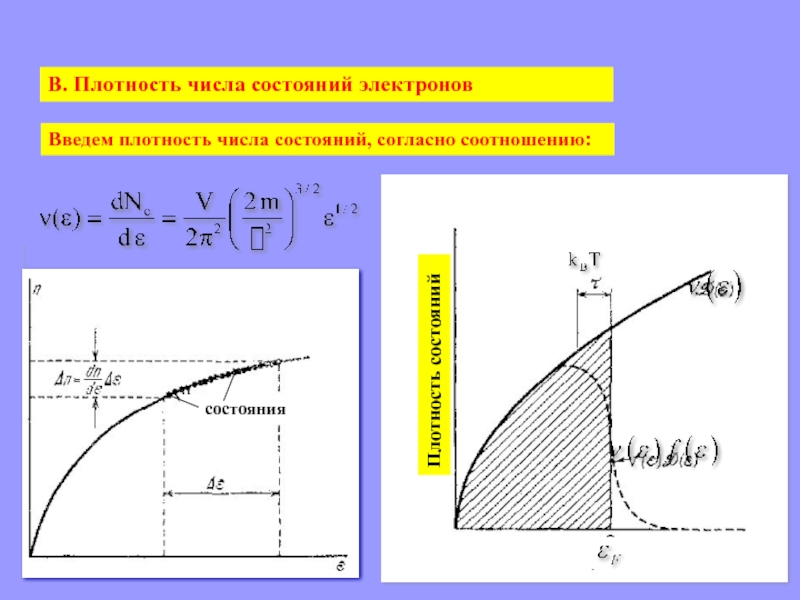
- 14. Введем плотность числа состояний, согласно соотношению:В. Плотность числа состояний электронов
- 15. Термодинамика свободного электронного газа В общем
- 16. Вся термодинамика электронного газа «разыгрывается» в тонком
- 17. Электроны в кристаллической решеткеВ кристалле электроны
- 18. Теорема Блоха решает вопрос о поведении электронов
- 19. Прежде всего заметим, что для свободных электронов
- 20. Образование запрещенных зон в кристаллеТаким образом, в
- 21. Классификация твердых тел (по зонной структуре)диэлектрикметаллполупроводник-
- 22. Классификация твердых тел (по зонной структуре)А).
- 23. Кинетические явления в электронном газа (металлы)Кинетика (физическая
- 24. Электропроводность электронного газа (металлы) Вычислим электропроводность электронного газа
- 25. ОткудаПо определению, плотность электрического тока естьТогдаВыше учтено,
- 26. Окончательно получаем известный закон Омагде величина электропроводности
- 27. Теплопроводность электронного газа (металлы)По определению, тепловой поток имеет видОткуда получаемТаким образом, теплопроводность электронов в металле есть:
- 28. Элементарные возбуждения и энергетический спектр конденсированного телаε,
- 29. Колебания кристаллической решеткиКолебания в одномерной цепочке (один атом в ячейке)nn-1n+1Вид продольных колебаний:
- 30. kωПри (длинные волны) :акустическая ветвь
- 31. MMmmMКолебания в одномерной цепочке (два атома в
- 32. - оптическая ветвь- акустическая ветвьАкустические и оптические моды
- 33. Фононы в конденсированном теле Понятие фононовT1ε, pЭлементарными
- 34. Фононный газФОНОНЫ (И.Е.Тамм, 1930г.) – низколежащие (по
- 35. В состоянии термодинамического равновесия среднее число фононов
- 36. Статистика и плотность состояний фононовСвободная энергия
- 37. Теплоемкость кристаллической решеткиНужно знать !!!1). случай высоких температурзакон Дюлонга-Пти
- 38. 2) случай низких температур=Число собственных колебаний в
- 39. закон Дебая, 1912г.
- 40. Дюлонг-ПтиДебай- температура Дебая- дебаевская частотаПочти всех веществ
- 41. Колебания кристалла – фононы (коллективные возбуждения -
- 42. Уравнения движения в приближении ближайших соседей:Решения уравнений движения:Гармоническое приближение – фононы не взаимодействуют !!!
- 43. Взаимодействие фононовВзаимодействие фононов – эффект негармоничности колебаний конденсированного тела – нет параболической потенциальной ямыНегармоничность(ангармоничность)
- 44. Механизмы рассеяния фононов: Рассеяние на границах образца; Рассеяние на дислокациях и дефектах; Фонон-фононное рассеяние0.010.11.0dT∝границыфононноерассеяниедефектыУвеличение концентрации дефектов
- 45. Уравнение Больцмана для фононовФункция распределения фононов: f
- 46. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ФИЗИКА КОНДЕНСИРОВАННОГО СОСТОЯНИЯ
Кафедра низких температур - Центр высоких технологий
МЭИ
(ТУ)
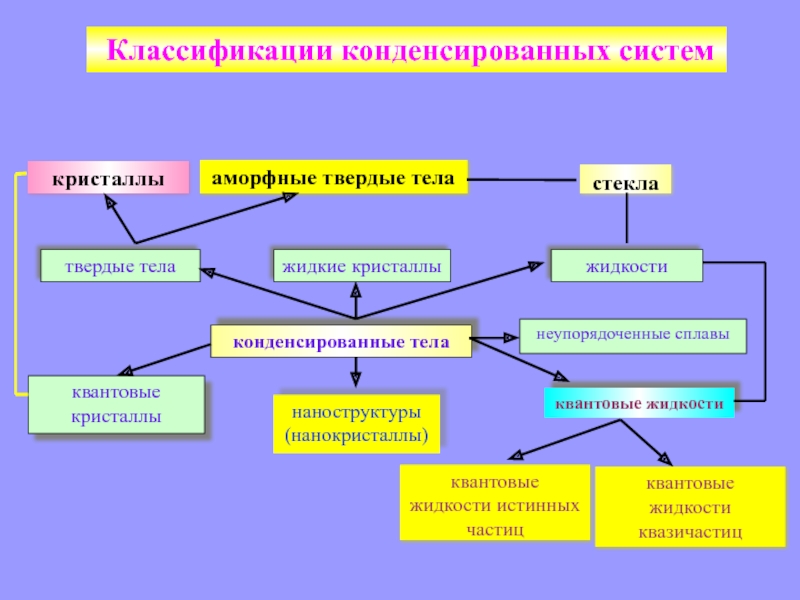
Слайд 2кристаллы
аморфные твердые тела
жидкие кристаллы
твердые тела
неупорядоченные сплавы
квантовые жидкости
квантовые кристаллы
конденсированные тела
наноструктуры (нанокристаллы)
квантовые
жидкости истинных частиц
квантовые жидкости квазичастиц
стекла
жидкости
Классификации конденсированных систем
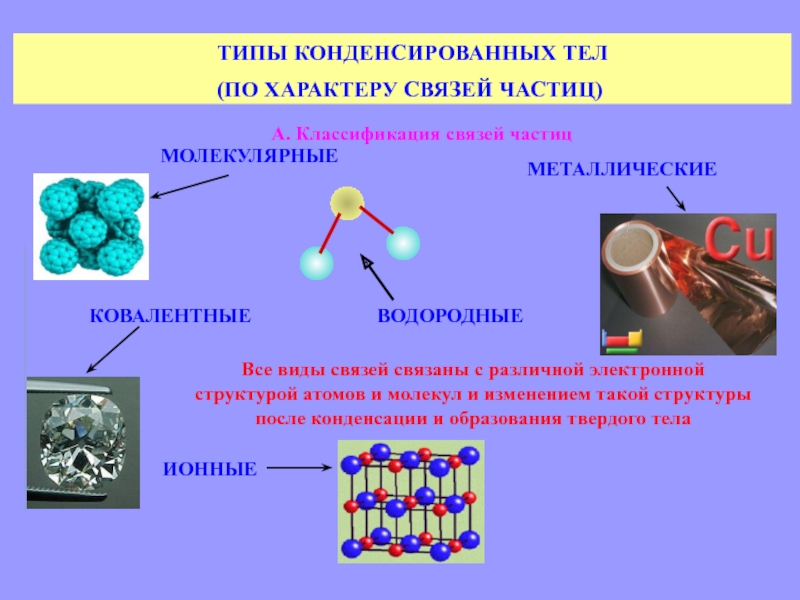
Слайд 3A. Классификация связей частиц
МОЛЕКУЛЯРНЫЕ
КОВАЛЕНТНЫЕ
МЕТАЛЛИЧЕСКИЕ
ИОННЫЕ
ТИПЫ КОНДЕНСИРОВАННЫХ ТЕЛ
(ПО ХАРАКТЕРУ
СВЯЗЕЙ ЧАСТИЦ)
Все виды связей связаны с различной электронной структурой атомов
и молекул и изменением такой структуры после конденсации и образования твердого телаВОДОРОДНЫЕ
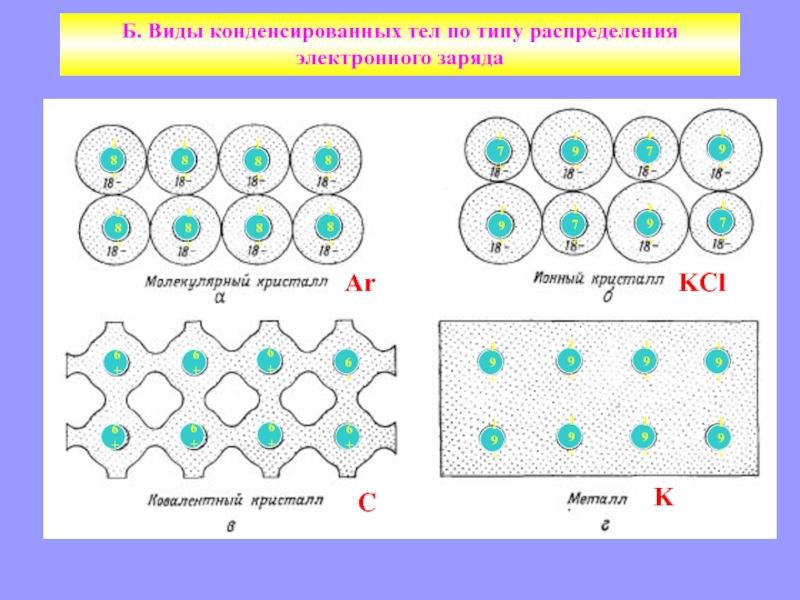
Слайд 4Ar
KCl
C
K
Б. Виды конденсированных тел по типу распределения электронного заряда
18+
18+
18+
18+
18+
18+
18+
18+
6+
6+
6+
6+
6+
6+
6+
6+
19+
19+
19+
17+
17+
17+
19+
17+
19+
19+
19+
19+
19+
19+
19+
19+
Слайд 7
а – межатомное расстояние; m – масса атома (иона); u0
– некоторая характерная величина, определяющая силу взаимодействия
Параметр де Бура
Слайд 8КВАНТОВАЯ СТАТИСТИКА
Статистическое описание систем многих частиц
Пусть система находится в
различных состояниях с энергией , тогда имеет место
распределение Гиббса для вероятности обнаружить систему (в целом) в состоянии n:Точное описание требует знания набора N значений . Если даже они известны, то через мгновение – необходимо знать снова эти величины - слишком подробное описание!!!
где A определяется условием нормировки:
Для систем классических частиц:
Следовательно, вероятности распределения по импульсам и по координатам – независимы!
Слайд 9Квантовая статистика
В системе многих квантовых частиц возникают новые типы статистик.
Несмотря на отсутствие прямого взаимодействия в системе квантовых частиц, имеют
место так называемые обменные эффекты, связанные со спином частиц. Если имеется N квантовых частиц в заданном объеме при температуре T, то их равновесное распределение описывается соотношением:Знак «+» соответствует частицам с полуцелым спином (фермионам), знак «-» - частицам с целым спином (бозонам), - химический потенциал, определяемый из условия:
где - плотность числа состояний, получаемая интегрированием по сфере , , где - спин частиц (1/2, 3/2,… - для фермионов и 0, 1,2,… - для бозонов).
Энергия системы квантовых частиц и их термодинамический потенциал выражаются соотношениями
Слайд 10Квантовая статистика Ферми-Дирака
В каждом энергетическом состоянии – две частицы с
противоспинами
Фермионы (ферми-газ) и слабовозбужденные состояния при низких температурах
Полная энергия ферми-газа
при T=0 есть pF называют фермиевским импульсом (заметим, что он не зависит от массы ферми-частиц и определяется только средним расстоянием между ними!)
квантовое распределение Ферми-Дирака
Слайд 11Квантовая статистика Бозе-Эйнштейна
Бозе-газ – газ частиц с целым спином по
своему поведению существенно отличается от ферми-газа. Прежде всего, в одном
и том же квантовом состоянии в бозе-газе может находится любое число частицСреднее число бозе-частиц, находящееся в состоянии с энергией
Если основное состояние (минимальное значение энергии) отвечает условию
Химический потенциал не может быть положительным, иначе некоторые из чисел заполнения окажутся отрицательными, что невозможно, поскольку всегда
всегда для бозе-частиц
если отношение достаточно мало, то число бозе-частиц на уровне может иметь порядок N
Слайд 12Электроны – фермионы – полуцелый спин => квантовая статистика Ферми
-Дирака
- волновая функция свободного электрона3. В объеме V электронные состояния квантованы, что отвечает определенному значению импульса, принимающего дискретные значения. В импульсном пространстве квантовые состояния делят весь объем V на микрообъемы так что число разрешенных состояний в импульсном пространстве равно:
Вырожденный электронный газ
ЭЛЕКТРОННАЯ ПОДСИСТЕМА
Слайд 13
А. Полная энергия электронного газа при нулевой температуре:
Б. Давление
электронного газа при этом можно найти из соотношения
Оценим давление
вырожденного ферми-газа, приняв, что плотность есть:электронов/см3, тогда получим P
Слайд 14
Введем плотность числа состояний, согласно соотношению:
В. Плотность числа состояний электронов
Слайд 15
Термодинамика свободного электронного газа
В общем случае, электронная подсистема,
находящаяся при ненулевой температуре, требует для расчета ее свойств знания
энергетического спектра. Поскольку фактически энергетический спектр электронов в конденсированном теле является непрерывным (расстояния между отдельными уровнями существенно меньше самих значений энергии), то можно перейти в исходных формулах для термодинамических величин от суммирования к интегрированию. Если воспользоваться понятием плотности числа электронных состояний, то получим (заметим, что интегрирование распространяется на всю область энергий; в запрещенных состояниях =0):
Слайд 16
Вся термодинамика электронного газа «разыгрывается» в тонком «пояске» вблизи энергии
Ферми !!!
Вычисления дают
Теплоемкость электронного газа:
Таким образом, в конденсированном теле,
где есть свободные электроны, общая теплоемкость складывается из фононной (закон Дебая) и электронной:
Слайд 17
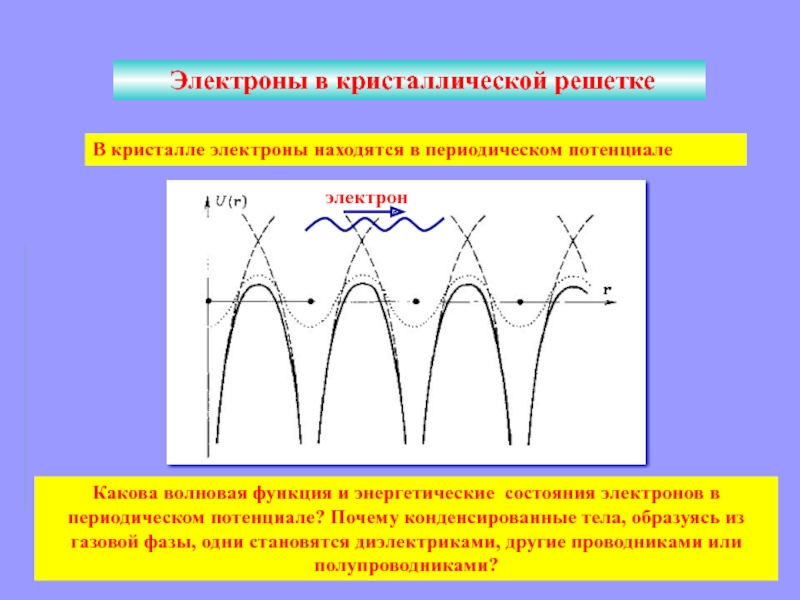
Электроны в кристаллической решетке
В кристалле электроны находятся в периодическом
потенциале
Какова волновая функция и энергетические состояния электронов в периодическом потенциале?
Почему конденсированные тела, образуясь из газовой фазы, одни становятся диэлектриками, другие проводниками или полупроводниками?электрон
Слайд 18
Теорема Блоха решает вопрос о поведении электронов в кристалле. Но,
она не дает ответа на вопрос, почему существуют проводники, полупроводники
и диэлектрики….. Теорема Блоха
(Ф.Блох, 1929г.)
- периодическая функция с периодом решетки
Энергетический спектр электронов в кристалле
Важнейшее следствие движения электронов в периодическом потенциале – наличие энергетических щелей (зон запрещенных состояний). Выясним качественно, откуда появляются такие зоны.
Периодический потенциал решетки
Слайд 19
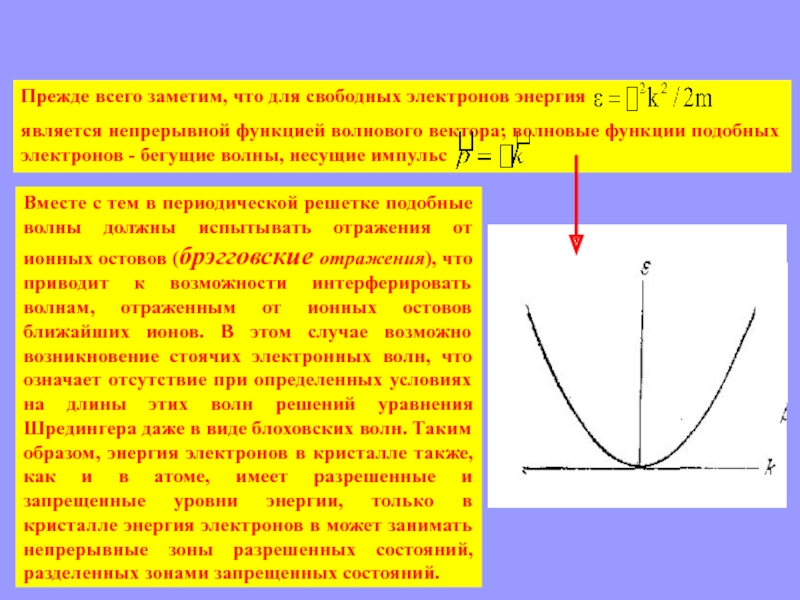
Прежде всего заметим, что для свободных электронов энергия
является непрерывной функцией волнового вектора; волновые функции
подобных электронов - бегущие волны, несущие импульс Вместе с тем в периодической решетке подобные волны должны испытывать отражения от ионных остовов (брэгговские отражения), что приводит к возможности интерферировать волнам, отраженным от ионных остовов ближайших ионов. В этом случае возможно возникновение стоячих электронных волн, что означает отсутствие при определенных условиях на длины этих волн решений уравнения Шредингера даже в виде блоховских волн. Таким образом, энергия электронов в кристалле также, как и в атоме, имеет разрешенные и запрещенные уровни энергии, только в кристалле энергия электронов в может занимать непрерывные зоны разрешенных состояний, разделенных зонами запрещенных состояний.
Слайд 20
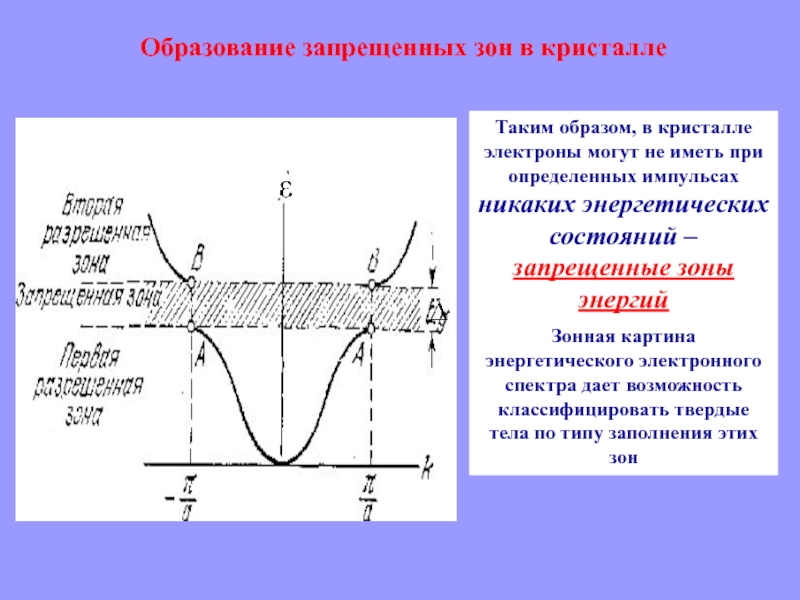
Образование запрещенных зон в кристалле
Таким образом, в кристалле электроны могут
не иметь при определенных импульсах никаких энергетических состояний – запрещенные
зоны энергийЗонная картина энергетического электронного спектра дает возможность классифицировать твердые тела по типу заполнения этих зон
Слайд 21
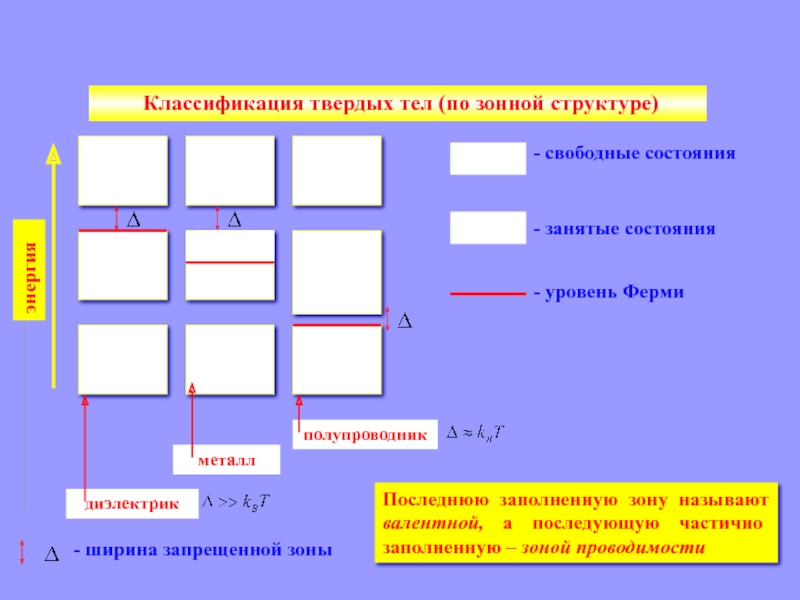
Классификация твердых тел (по зонной структуре)
диэлектрик
металл
полупроводник
- ширина запрещенной зоны
-
свободные состояния
- занятые состояния
- уровень Ферми
энергия
Последнюю заполненную зону называют валентной,
а последующую частично заполненную – зоной проводимости
Слайд 22
Классификация твердых тел (по зонной структуре)
А). Диэлектрики
Если последняя
из разрешенных зон полностью заполнена электронами, но все более высокие
по энергии зоны целиком свободны, то такие тела называются диэлектрикам (изоляторами); для типичного изолятора – алмаза:Б). Полупроводники
В полупроводниках при T=0 валентная зона полностью заполнена, а зона проводимости – свободна, аналогично диэлектрикам; для типичного полупроводника Si :
В). Металлы
Если последняя разрешенная зона заполнена неполностью, то в этом случае даже слабое внешнее электрическое поле вызывает появление электрического тока. Такие тела носят название металлов; типичными металлами являются щелочные (Li, Na, K, Cs, Rb), а также благородные (Cu, Ag, Au).
Слайд 23
Кинетические явления в электронном газа (металлы)
Кинетика (физическая кинетика) – наука
о неравновесных свойствах конденсированных тел, т.е. в отсутствии термодинамического равновесия
Температура
в точке 1 выше, чем в точке 2или
электрический потенциал
в точке 1 выше, чем в точке 2
2
1
(нарушенное термодинамическое равновесие !)
Кинетическое уравнение Больцмана для электронов
Интеграл столкновений (учитывает столкновения электронов между собой, с фононами, дефектами и примесями)
Слайд 24
Электропроводность электронного газа (металлы)
Вычислим электропроводность электронного газа в металлах. Будем
считать, что во внешнем электрическом поле распределение электронов по координатам
не меняется, а меняется только по импульсам. Тогда из уравненияПолучаем:
где принято, что
f0 – равновесная функция распределения для электронов. Полагая, что
Получаем из
Но
Слайд 25
Откуда
По определению, плотность электрического тока есть
Тогда
Выше учтено, что равновесная функция
распределения – четная функция энергии и интеграл от нее равен
нулю. После интегрирования по углам и учете того, что , получаемСлайд 26
Окончательно получаем известный закон Ома
где величина электропроводности есть
При этом учтено,
что
Таким образом, электропроводность зависит только от времени релаксации и
плотности электронов Слайд 27
Теплопроводность электронного газа (металлы)
По определению, тепловой поток имеет вид
Откуда получаем
Таким
образом, теплопроводность электронов в металле есть:
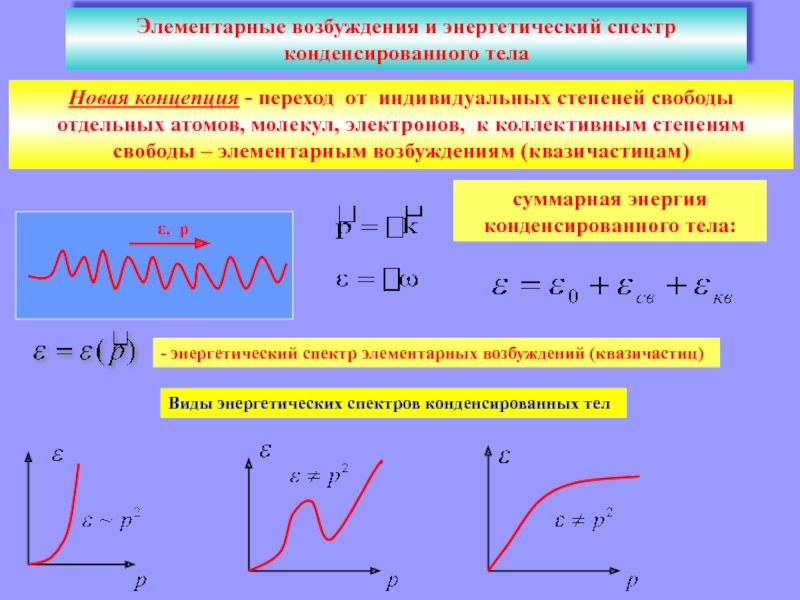
Слайд 28Элементарные возбуждения и энергетический спектр конденсированного тела
ε, p
Новая концепция -
переход от индивидуальных степеней свободы отдельных атомов, молекул, электронов, к
коллективным степеням свободы – элементарным возбуждениям (квазичастицам)- энергетический спектр элементарных возбуждений (квазичастиц)
Виды энергетических спектров конденсированных тел
суммарная энергия конденсированного тела:
Слайд 29
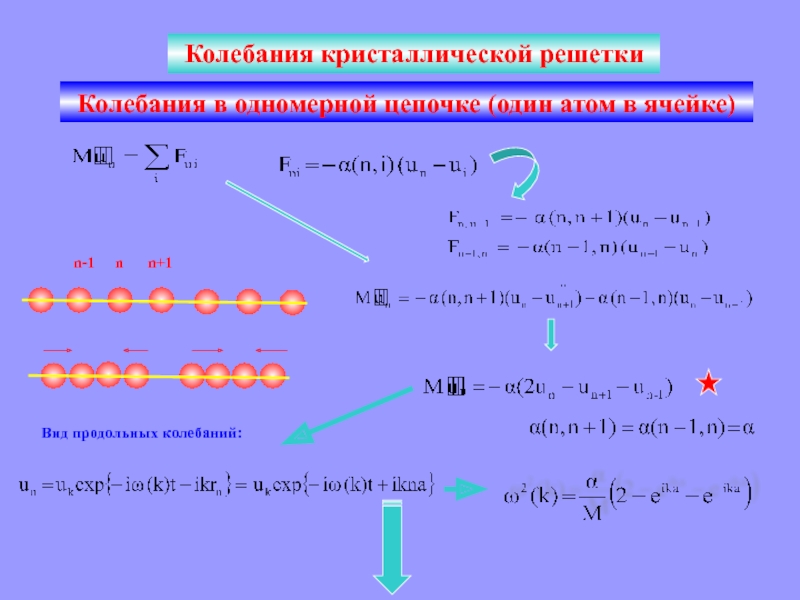
Колебания кристаллической решетки
Колебания в одномерной цепочке (один атом в ячейке)
n
n-1
n+1
Вид
продольных колебаний:
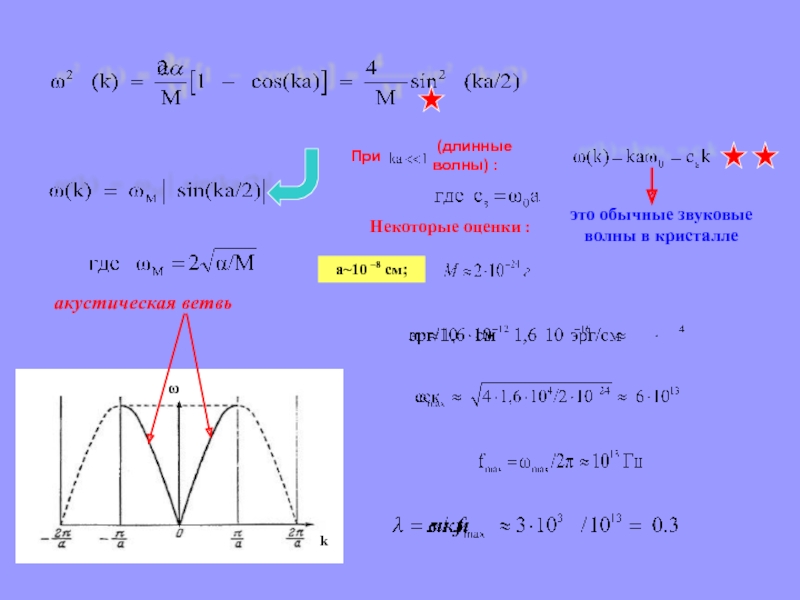
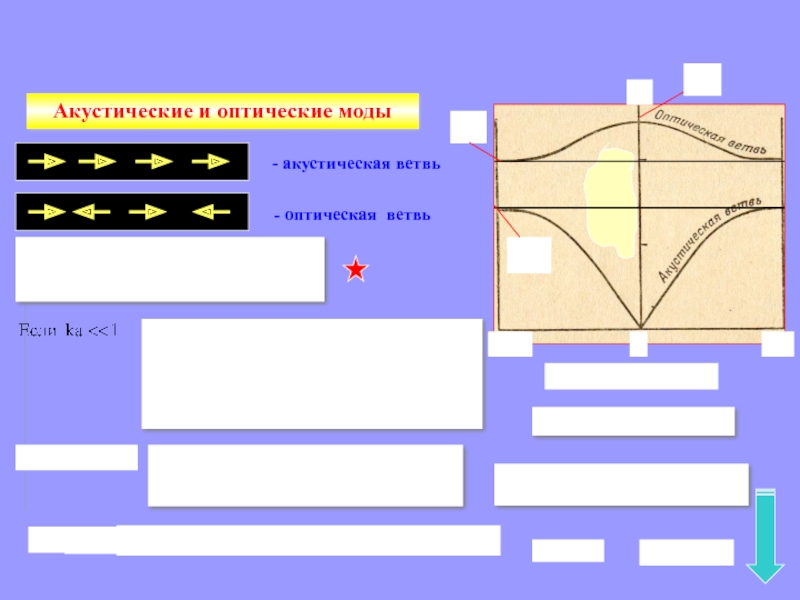
Слайд 30
k
ω
При
(длинные волны) :
акустическая ветвь
Некоторые оценки :
a~10
–8 cм;
это обычные звуковые волны в кристалле
Слайд 31
M
M
m
m
M
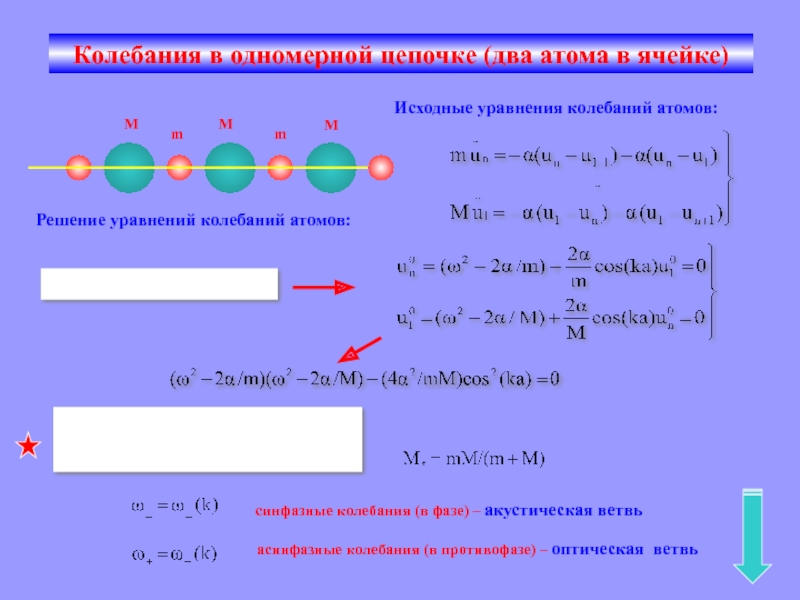
Колебания в одномерной цепочке (два атома в ячейке)
Исходные уравнения колебаний
атомов:
Решение уравнений колебаний атомов:
асинфазные колебания (в противофазе) – оптическая ветвь
синфазные
колебания (в фазе) – акустическая ветвь
Слайд 33Фононы в конденсированном теле
Понятие фононов
T1
ε, p
Элементарными возбуждениями
в кристаллических телах
являются коллективные смещения атомов решетки из положений равновесия
Тепловое возбуждение
конденсированного телаПереход от индивидуальных движений атомов к коллективным степеням свободы
В любой системе взаимодействующих атомов элементарными возбуждениями
(если система возбуждена достаточно слабо, например, находится при низких
температурах) являются коллективные смещения атомов из положений равновесия.
T1 > T2
!!!
Теорема:
Слайд 34Фононный газ
ФОНОНЫ (И.Е.Тамм, 1930г.) – низколежащие (по энергетическим уровням) коллективные
возбуждения кристаллической решетки
В конденсированном теле при нулевой температуре фононы
отсутствуют (положение атомов в узлах – основное состояние конденсированного тела - является вакуумом для фононов), а их появление связано с нагревом тела С ростом температуры число фононов растет и их число в коллективном движении атомов является весьма большой (макроскопической) величиной. Таким образом, возникает картина большого числа фононов как носителей коллективного возбуждения конденсированного тела. Поскольку фононы могут возбуждаться поодиночке, а значит, имеют целый спин, то они являются бозе-частицами и подчиняются в ансамбле статистике Бозе-Эйнштейна. Следует также заметить, что введение фононов только тогда имеет смысл, если они между собой либо вообще не взаимодействуют, либо взаимодействуют слабо. Следовательно, сам ансамбль фононов можно рассматривать как газ. В этом случае общую энергию конденсированного тела можно рассматривать как сумму энергии основного состояния – энергия связи атомов в положении равновесия и энергия нулевых (квантовых) колебаний атомов (вакуум для фононов) и суммы энергий отдельных фононов:
В кристаллах может быть несколько типов фононов (например, акустические и оптические, причем при наличии в ячейке j атомов – 3j типов фононов
Слайд 35В состоянии термодинамического равновесия среднее число фононов
ветви i
с волновым вектором
С точки зрения
квантовой (и классической) механики, нормальные колебания решетки ведут себя как набор независимых гармонических осцилляторов. Роль координаты осциллятора играет при этом амплитуда колебания, число фононов является уровнем энергии осциллятора На каждое колебание приходится средняя энергия
При высоких температурах
число фононов пропорционально температуре
.
.
среднее число фононов экспоненциально мало:
Если
Слайд 36 Статистика и плотность состояний фононов
Свободная энергия тела есть:
- плотность состояний фононов (число состояний фононов на
интервал частот ).
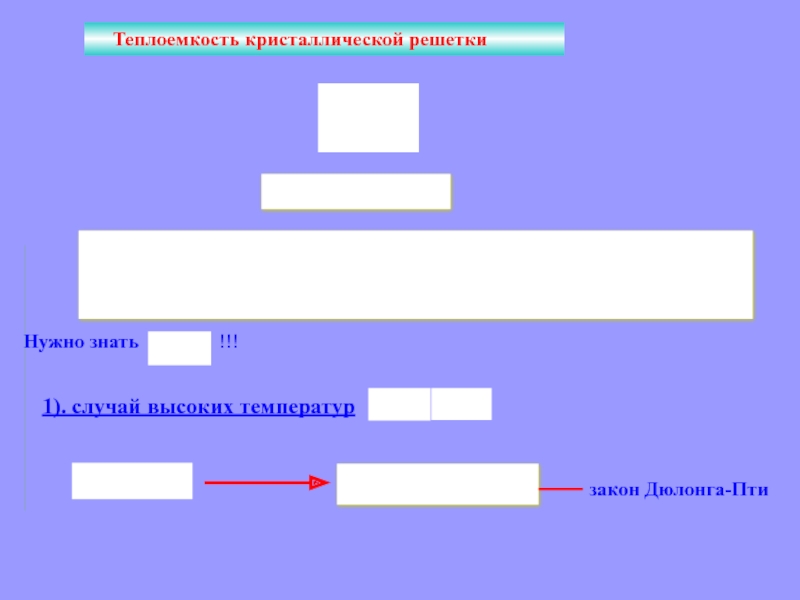
Слайд 37Теплоемкость кристаллической решетки
Нужно знать
!!!
1). случай высоких температур
закон Дюлонга-Пти
Слайд 38
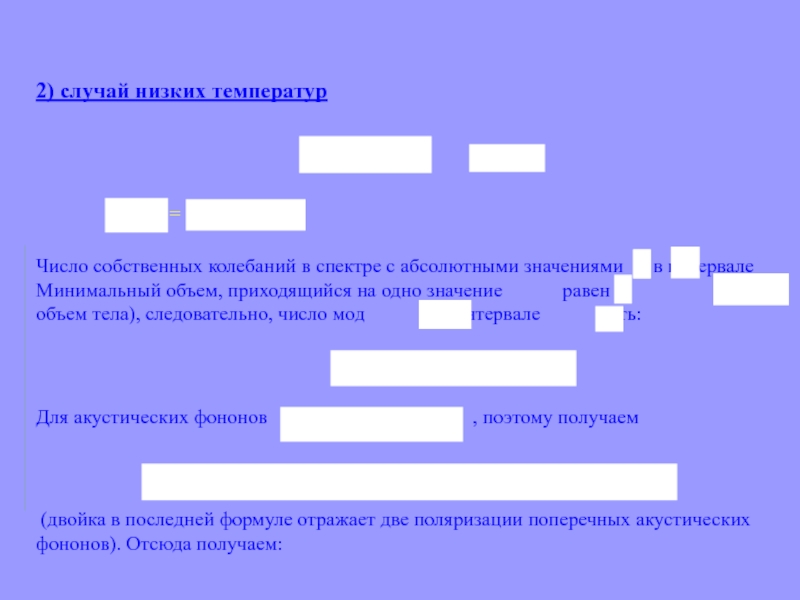
2) случай низких температур
=
Число собственных колебаний в спектре с абсолютными
значениями в интервале Минимальный объем, приходящийся на одно
значение равен (V – объем тела), следовательно, число мод в интервале есть:Для акустических фононов , поэтому получаем
(двойка в последней формуле отражает две поляризации поперечных акустических фононов). Отсюда получаем:
Слайд 40
Дюлонг-Пти
Дебай
- температура Дебая
- дебаевская частота
Почти всех веществ температура Дебая существенно
ниже температуры плавления. Вместе с тем, существуют кристаллы (в частности,
He под давлением), когда выполняется условие ( -температура плавления). В этом случае, очевидно, невозможно классическое описание поведения атомов конденсированного тела.
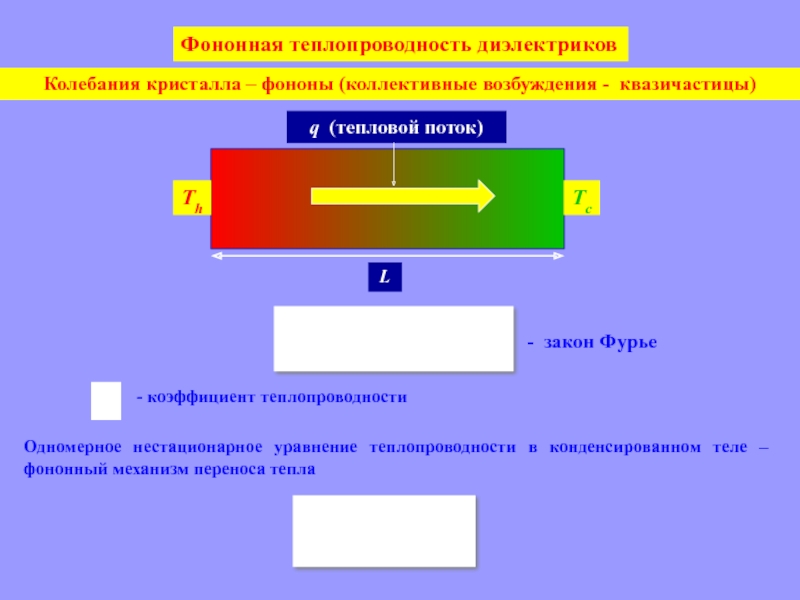
Слайд 41Колебания кристалла – фононы (коллективные возбуждения - квазичастицы)
q (тепловой поток)
Th
Tc
L
-
коэффициент теплопроводности
Одномерное нестационарное уравнение теплопроводности в конденсированном теле – фононный
механизм переноса тепла - закон Фурье
Фононная теплопроводность диэлектриков
Слайд 42Уравнения движения в приближении ближайших соседей:
Решения уравнений движения:
Гармоническое приближение –
фононы не взаимодействуют !!!
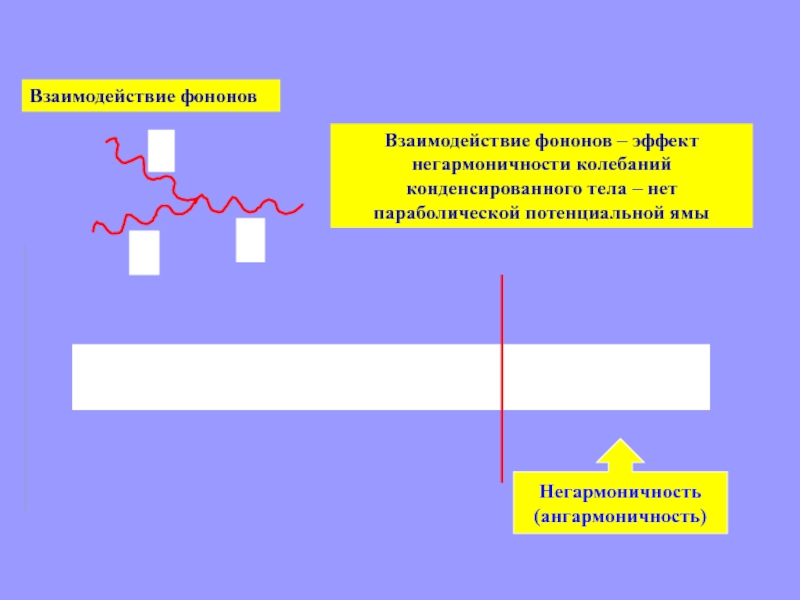
Слайд 43Взаимодействие фононов
Взаимодействие фононов – эффект негармоничности колебаний конденсированного тела –
нет параболической потенциальной ямы
Негармоничность
(ангармоничность)
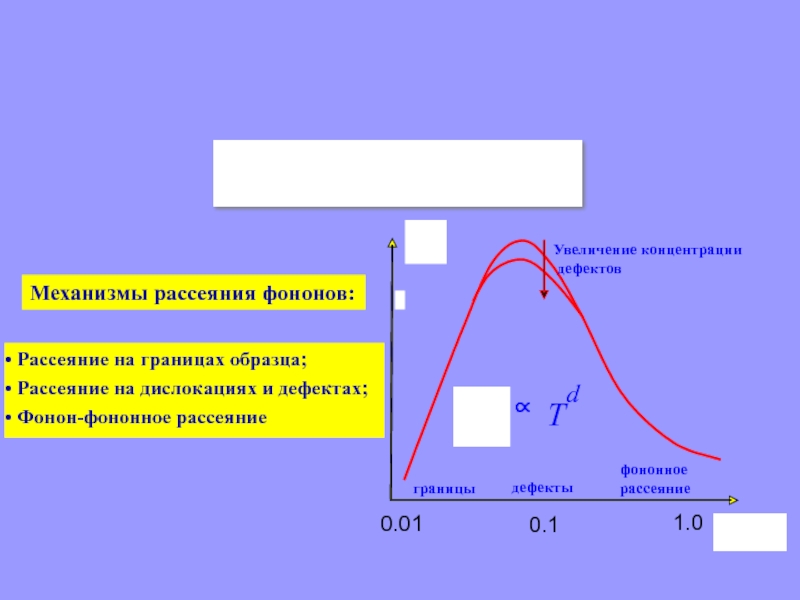
Слайд 44Механизмы рассеяния фононов:
Рассеяние на границах образца;
Рассеяние на дислокациях
и дефектах;
Фонон-фононное рассеяние
0.01
0.1
1.0
d
T
∝
границы
фононное
рассеяние
дефекты
Увеличение концентрации
дефектов
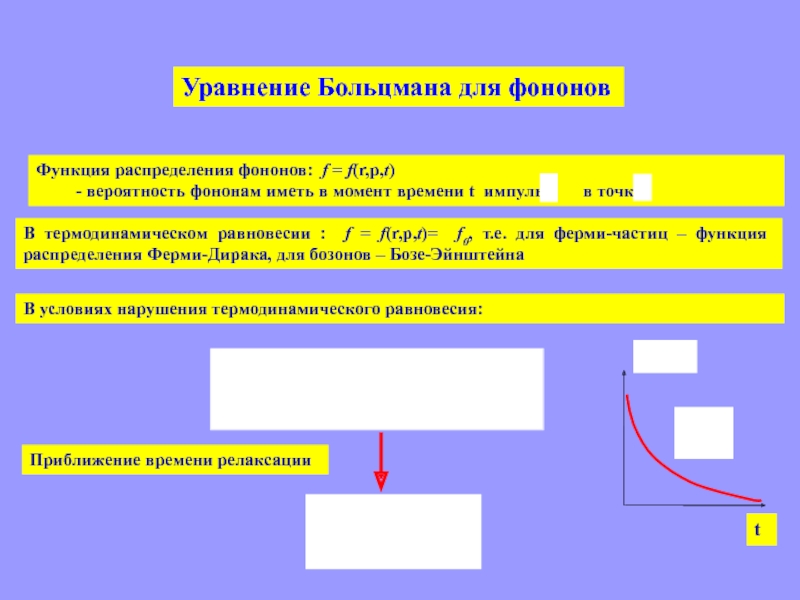
Слайд 45Уравнение Больцмана для фононов
Функция распределения фононов: f = f(r,p,t)
- вероятность
фононам иметь в момент времени t импульс
в точкеВ термодинамическом равновесии : f = f(r,p,t)= f0, т.е. для ферми-частиц – функция распределения Ферми-Дирака, для бозонов – Бозе-Эйнштейна
В условиях нарушения термодинамического равновесия:
Приближение времени релаксации
t