Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Колебания и волны
Содержание
- 1. Колебания и волны
- 2. Тема 10. ПОЛЯРИЗАЦИЯ СВЕТА10.1. Естественный и поляризованный
- 3. 10.1. Естественный и поляризованный свет Основным свойством электромагнитных
- 4. Естественный свет – неполяризованный:Линейная поляризация:Электромагнитная волна в
- 5. Линейно поляризованная электромагнитная волна и волна круговой поляризации.
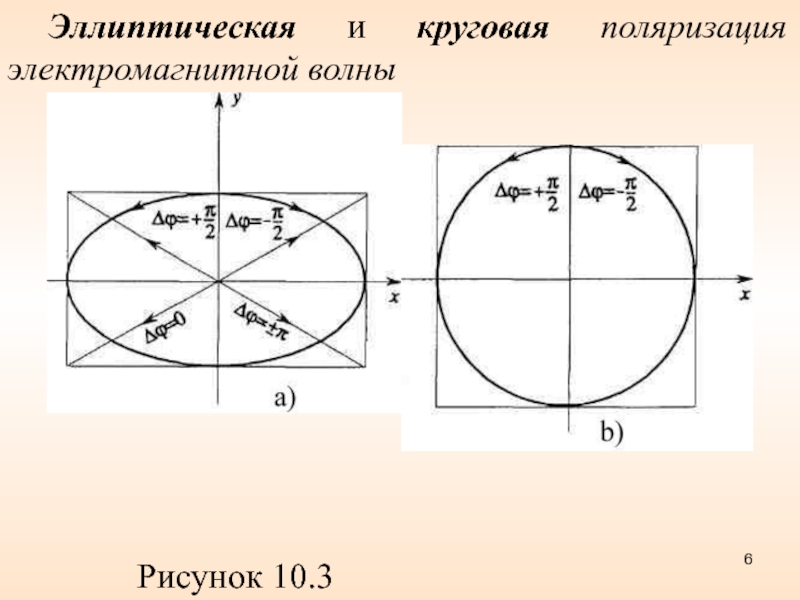
- 6. Эллиптическая и круговая поляризация электромагнитной волны Рисунок 10.3
- 7. Пространственная структура эллиптически -поляризованных
- 8. Образование поляризованного света Рассмотрим 2
- 9. Слайд 9
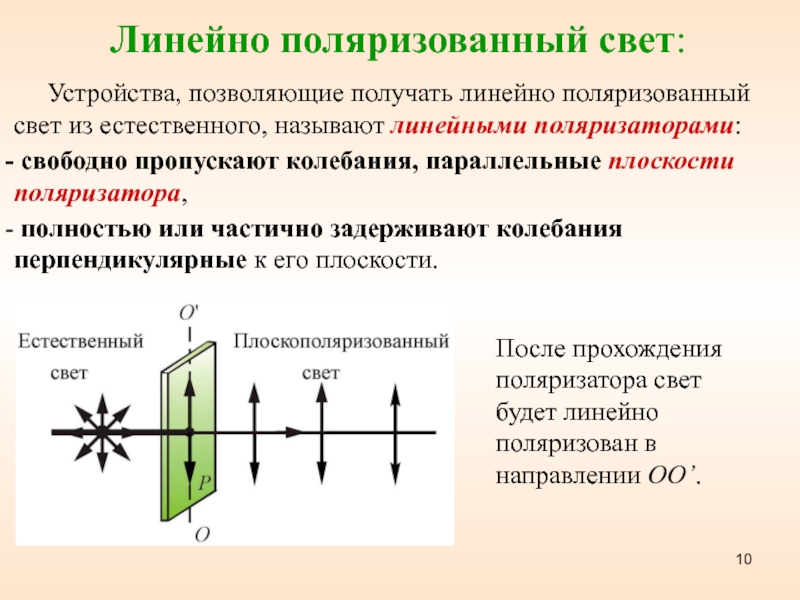
- 10. Линейно поляризованный свет:
- 11. Линейные поляризаторы: оптически анизотропные кристаллы (турмалин), вырезанные
- 12. Слайд 12
- 13. Полихромные кристаллы турмалина
- 14. Слайд 14
- 15. Возможность изменения яркости и контраста различных частей
- 16. Слайд 16
- 17. В реальных средах возможно превращение неполяризованных волн
- 18. Аналогичное устройство, применяемое для
- 19. Рисунок 10.5 После прохождения поляризатора
- 20. • световые волны поперечны, однако в естественном
- 21. 10.2. Поляризация при отражении ипреломлении В этом и
- 22. В отраженном луче преобладают колебания, перпендикулярные плоскости
- 23. то отраженный луч оказывается полностью поляризованным.
- 24. Формулы Френеля При падении
- 25. французский физикБроли, Франция (Broglie, France)Ville-d'Avray, FranceОгюстен Жан ФренельAugustin Jean Fresnel10.05.1788 – 14.07.1827
- 26. 10.3. Двойное преломление света В 1669 г. датский
- 27. нидерландский механик, физик и математикГаага, Нидерланды (Hague, Netherlands)Христиан ГюйгенсChristiaan Huygens14.04.1629 – 08.08.1695
- 28. Объяснение этого явления дал современник Бартолина −
- 29. Закон преломления Снеллиуса: Подчиняется
- 30. Рисунок 10.8 Явление двойного лучепреломления используется для получения поляризованного света:
- 31. Слайд 31
- 32. Дихроизм – один из лучей поглощается сильнее
- 33. В качестве поляроида
- 34. Двойное лучепреломление
- 35. Слайд 35
- 36. Поскольку , а в диэлектриках μ =
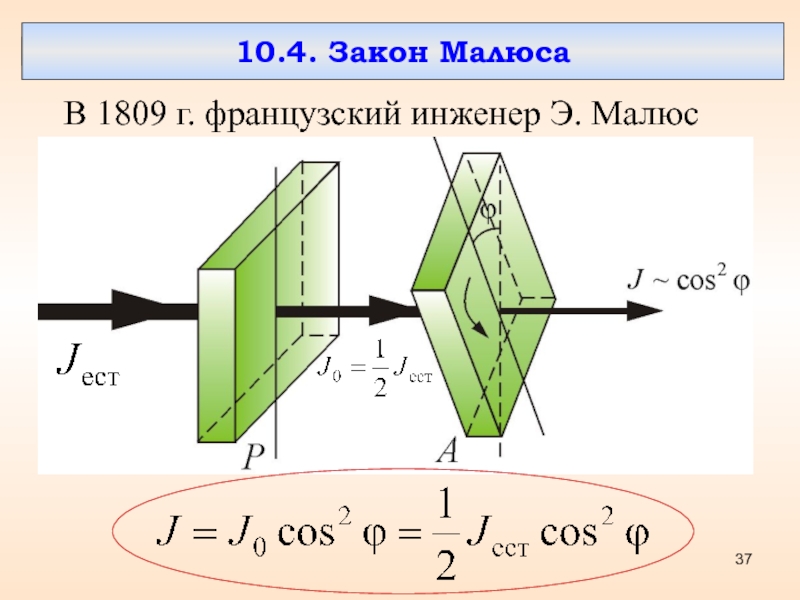
- 37. 10.4. Закон МалюсаВ 1809 г. французский инженер Э. Малюс
- 38. В поперечной волне направление
- 39. С помощью разложения векторана составляющие по осям можно объяснить закон Малюса Рисунок 10.12
- 40. Световую волну с амплитудой разложим на
- 41. Рис. 11. Прохождение естественного света через два идеальных поляроида. yy' – разрешенные направления поляроидов
- 42. После первого поляризатора Второй поляризатор пропустит свет
- 43. Прохождение линейно поляризованного света He-Ne лазера через
- 44. Эллипсометрия - изучение поверхностей жидких и твёрдых
- 45. Микроскопия с использованием принципов эллипсометрии Излучение лазера
- 46. Слайд 46
- 47. 10.5. Интерференция поляризованного света Явления интерференции поляризованных лучей
- 48. Араго Доминик Франсуа (26.II.1786 - 2.X.1853) -
- 49. Анализатор А здесь необходим также, для того
- 50. 10.6. Искусственная анизотропия Двойное
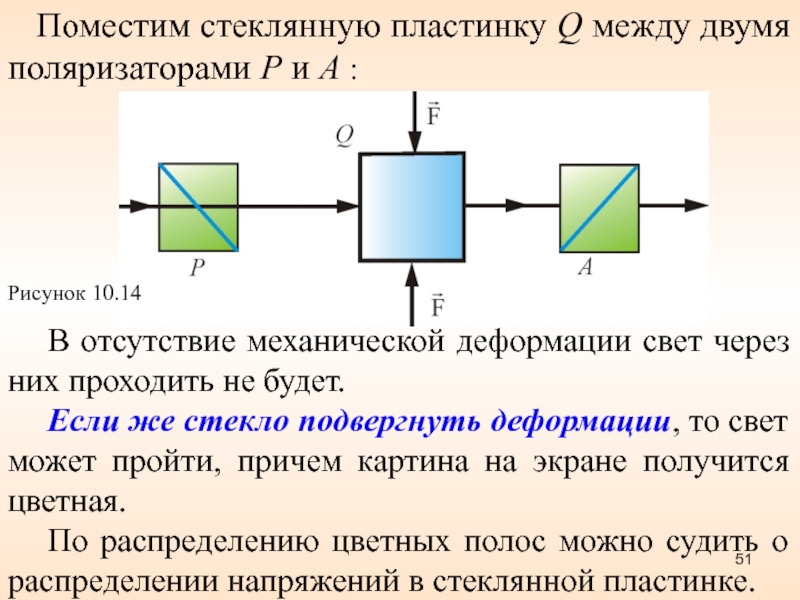
- 51. Поместим стеклянную пластинку Q между
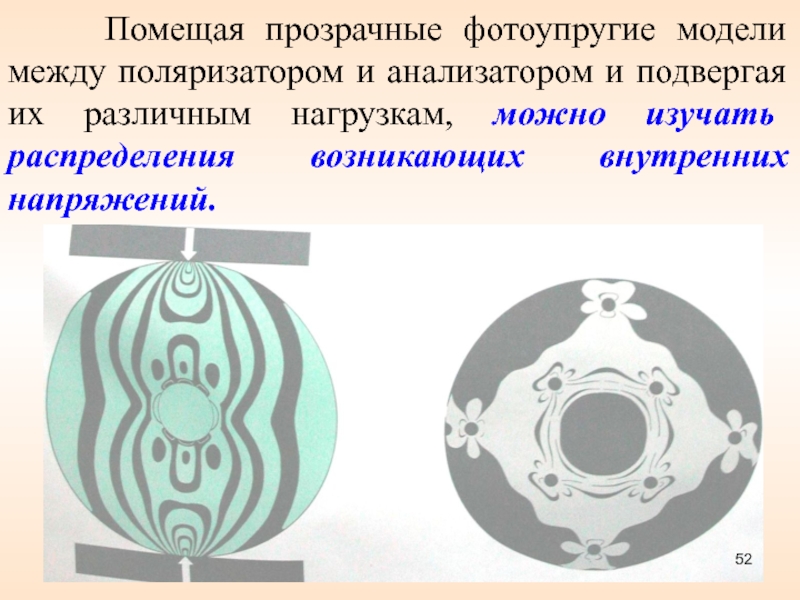
- 52. Помещая прозрачные фотоупругие модели
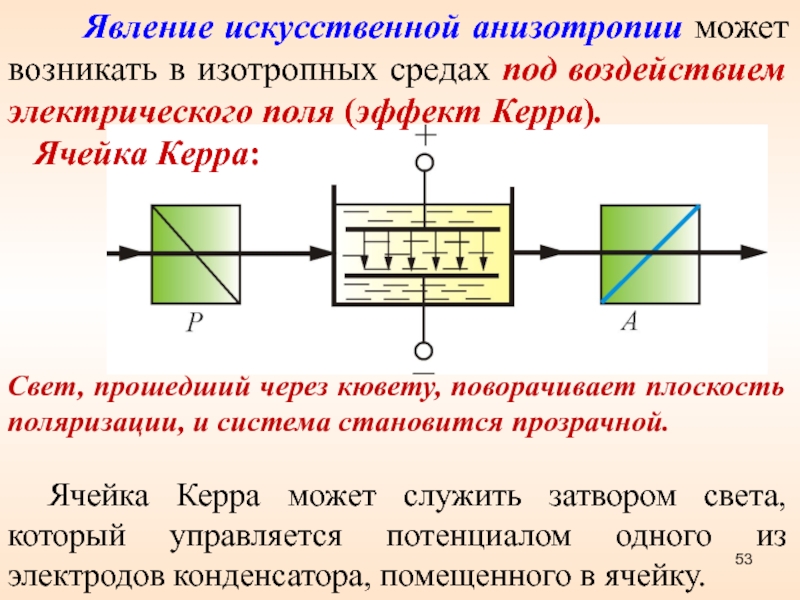
- 53. Явление искусственной анизотропии
- 54. На основе ячеек
- 55. 10.7. Вращение плоскости поляризацииОптически активные вещества –
- 56. В кристаллах:(сильнее всего вращают плоскость поляризации, если
- 57. Лекция окончена!
- 58. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Тема 10. ПОЛЯРИЗАЦИЯ СВЕТА
10.1. Естественный и поляризованный свет
Сегодня: *
10.2. Поляризация
при отражении и
преломлении
10.3. Двойное преломление света
10.4. Закон Малюса
10.5. Интерференция поляризованного
света10.6. Искусственная анизотропия
Слайд 310.1. Естественный и поляризованный свет
Основным свойством электромагнитных волн является поперечность
колебаний векторов напряжённости электрического и магнитного полей
Рисунок 10.1
Продольная волна
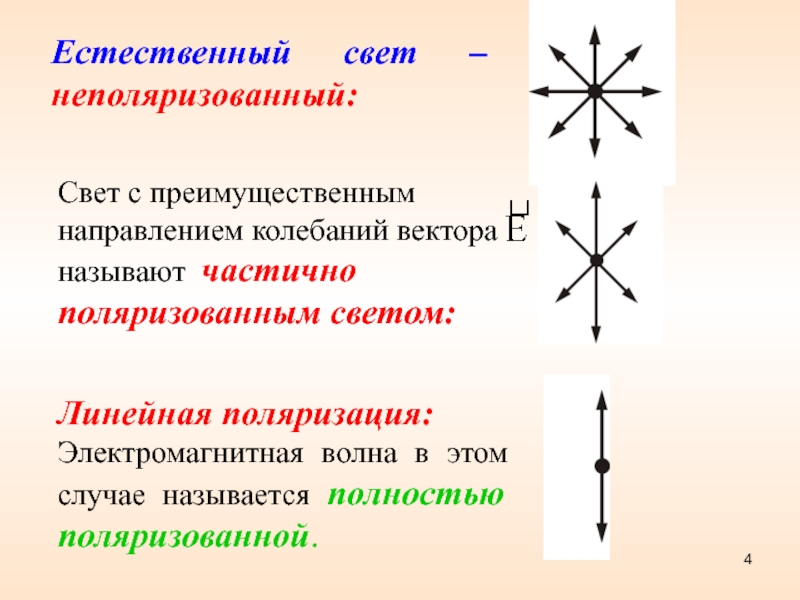
всегда симметрична относительно направления распространения. Слайд 4Естественный свет – неполяризованный:
Линейная поляризация:
Электромагнитная волна в этом случае называется
полностью поляризованной.
Свет с преимущественным направлением колебаний вектора
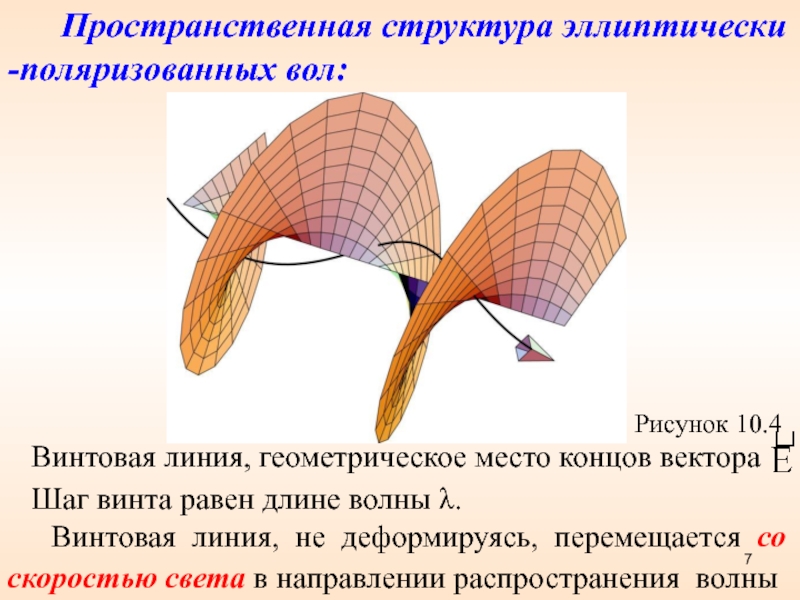
называют частично поляризованным светом:Слайд 7 Пространственная структура эллиптически -поляризованных вол:
Рисунок 10.4
Винтовая линия, геометрическое место концов вектора
Шаг винта
равен длине волны λ. Винтовая линия, не деформируясь, перемещается со скоростью света в направлении распространения волны
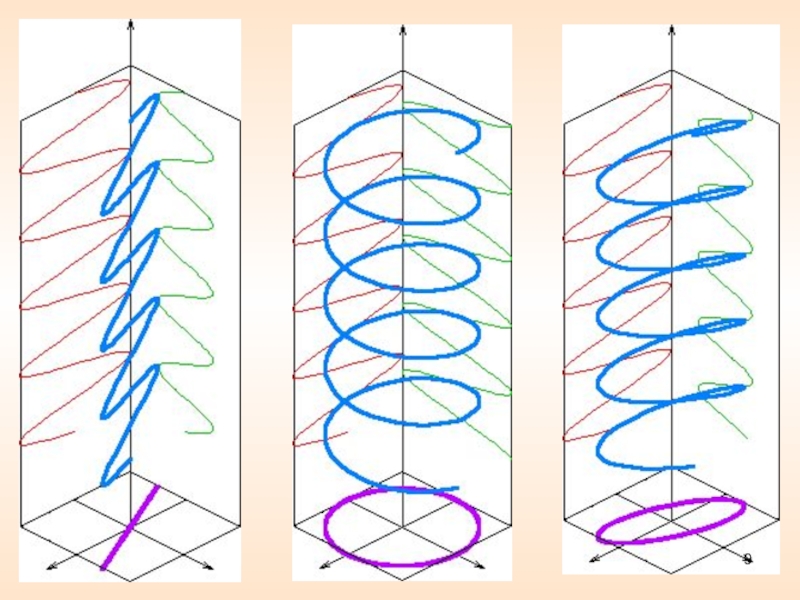
Слайд 8 Образование поляризованного света
Рассмотрим 2 взаимно перпендикулярных колебания,
отличающихся по фазе на α:
Результат сложения:
α = 0 или π
– плоскополяризованный свет;А1 = А2 и - свет, поляризованный по кругу;
произвольные А и α – эллиптически поляризованный свет.
Слайд 10Линейно поляризованный свет:
Устройства,
позволяющие получать линейно поляризованный свет из естественного, называют линейными поляризаторами:
свободно пропускают колебания, параллельные плоскости поляризатора, полностью или частично задерживают колебания перпендикулярные к его плоскости.
После прохождения поляризатора свет будет линейно поляризован в направлении ОО’.
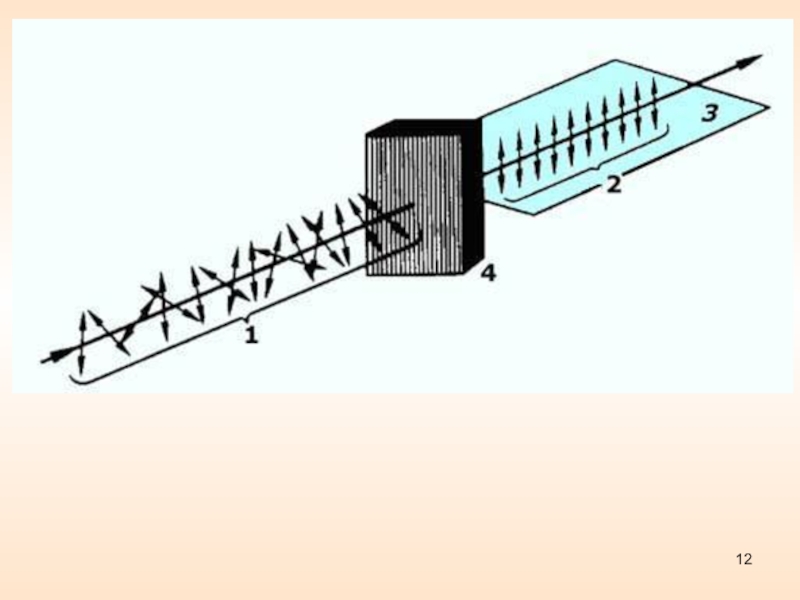
Слайд 11Линейные поляризаторы:
оптически анизотропные кристаллы (турмалин), вырезанные параллельно его оптической
оси;
поляроиды – целлулоидные плёнки, в которые введено большое количество одинаково
ориентированных с помощью растяжения или сдвиговой деформации кристалликов. оптические стопы изотропных пластинок, прозрачных в нужной области спектра.
Слайд 15 Возможность изменения яркости и контраста различных частей изображения:
получение тёмного,
густо-синего неба в солнечный день;
избавление от отражения фотографа в
стекле при съёмке находящихся за стеклом объектов. Пример использования поляризационного фильтра в фотографии
Слайд 17 В реальных средах возможно превращение неполяризованных волн в полностью поляризованные
и наоборот.
Способы поляризации:
Поляризация электромагнитной волны
при отражении и преломлении. Поляризация при распространении электромаг-нитных волн в оптически анизотропных средах.
Ассиметрию поперечных световых лучей можно изучать, пропуская свет через анизотропные кристаллы.
Устройства позволяющие получать линейно поляризованный свет, называют поляризаторами.
Для анализа поляризации света, используют анализаторы.
Главная плоскость поляризатора (анализатора).
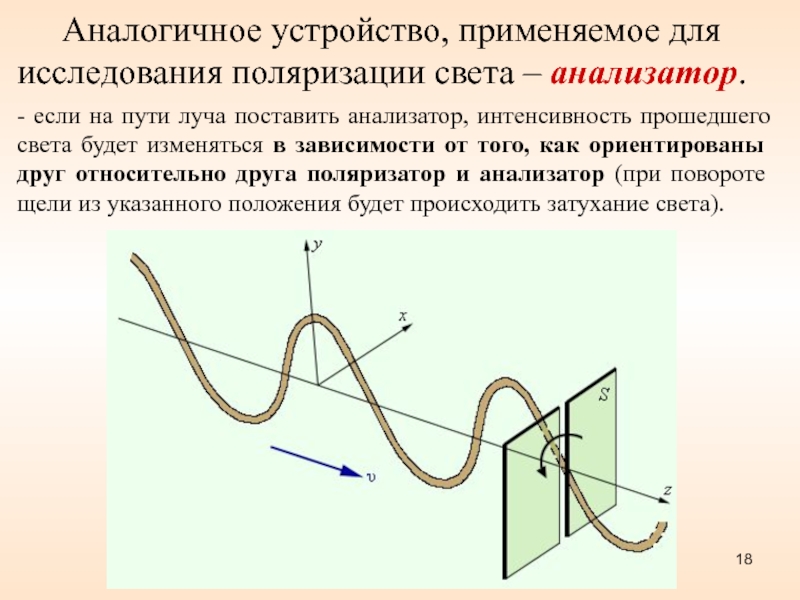
Слайд 18 Аналогичное устройство, применяемое для исследования поляризации света
– анализатор.
- если на пути луча поставить анализатор, интенсивность прошедшего
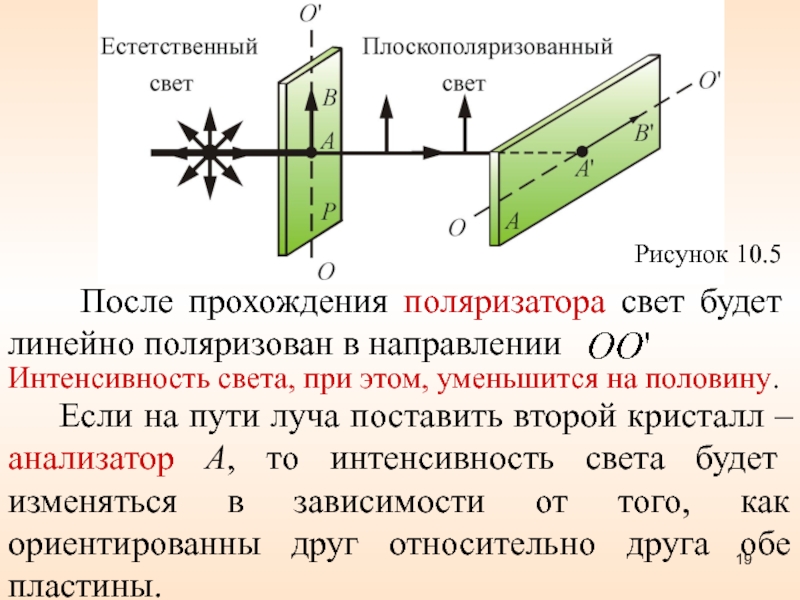
света будет изменяться в зависимости от того, как ориентированы друг относительно друга поляризатор и анализатор (при повороте щели из указанного положения будет происходить затухание света). Слайд 19Рисунок 10.5
После прохождения поляризатора свет будет
линейно поляризован в направлении
Интенсивность света, при этом, уменьшится на
половину. Если на пути луча поставить второй кристалл – анализатор A, то интенсивность света будет изменяться в зависимости от того, как ориентированны друг относительно друга обе пластины.
Слайд 20• световые волны поперечны, однако в естественном свете нет преимущественного
направления колебаний;
• кристалл поляризатора пропускает лишь те волны, вектор
которых имеет составляющуюпараллельную оси кристалла. (именно поэтому поляризатор ослабляет свет в два раза);
• для анализа света используется кристалл анализатора, который, пропускает свет, когда его ось параллельна оси поляризатора.
Основные выводы
Слайд 2110.2. Поляризация при отражении и
преломлении
В этом и следующем параграфах мы
рассмотрим способы получения линейно поляризованного света, используемые при изготовлении поляризаторов
и анализаторов.Свет поляризуется при отражении от границы двух сред и при прохождении границы – при преломлении.
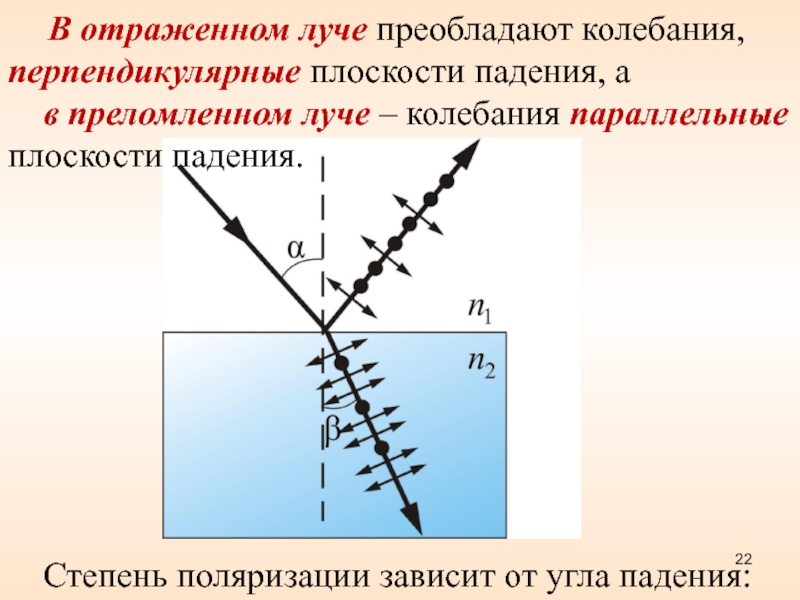
В отраженном луче преобладают колебания, перпендикулярные плоскости падения, а в преломленном луче – колебания параллельные плоскости падения
Слайд 22 В отраженном луче преобладают колебания, перпендикулярные плоскости падения, а
в преломленном луче – колебания параллельные плоскости падения.
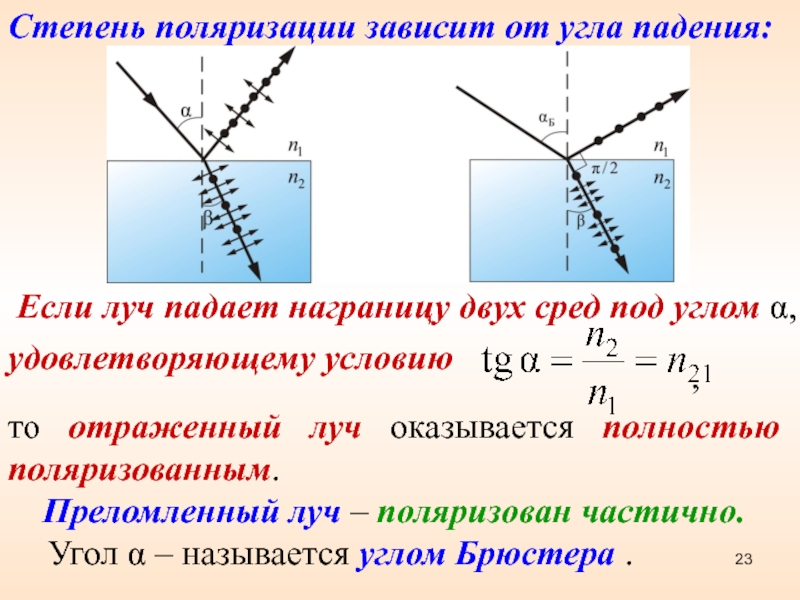
Степень поляризации зависит от угла падения:Слайд 23
то отраженный луч оказывается полностью поляризованным.
Преломленный
луч – поляризован частично.
Угол α – называется углом Брюстера .
Если луч падает награницу двух сред под углом α, удовлетворяющему условию
,
Степень поляризации зависит от угла падения:
Слайд 24Формулы Френеля
При падении естественного света на
границу раздела двух диэлектриков:
для отраженного луча:
для преломленного луча: Степень поляризации можно записать как
Слайд 25французский физик
Броли, Франция (Broglie, France)
Ville-d'Avray, France
Огюстен Жан Френель
Augustin Jean Fresnel
10.05.1788
– 14.07.1827
Слайд 2610.3. Двойное преломление света
В 1669 г. датский ученый Эразм Бартолин
опубликовал работу, в которой сообщил об открытии нового физического явления
– двойного преломления света.В кристалле исландского шпата Бартолин обнаружил, что луч внутри кристалла расщепляется на два луча :
Рисунок 10.7
Слайд 27нидерландский механик, физик и математик
Гаага, Нидерланды (Hague, Netherlands)
Христиан Гюйгенс
Christiaan Huygens
14.04.1629
– 08.08.1695
Слайд 28 Объяснение этого явления дал современник Бартолина − голландский ученый Христиан
Гюйгенс.
Расщепление луча света, проходящего через исландский шпат, связано с
анизотропией кристалла. У анизотропных кристаллов имеется
оптическая ось.
Одноосные кристаллы (исландский шпат, турмалин)
Плоскость, проходящая через оптическую ось, называется главным сечением кристалла
Кристаллы двухосные (гипс, слюда).
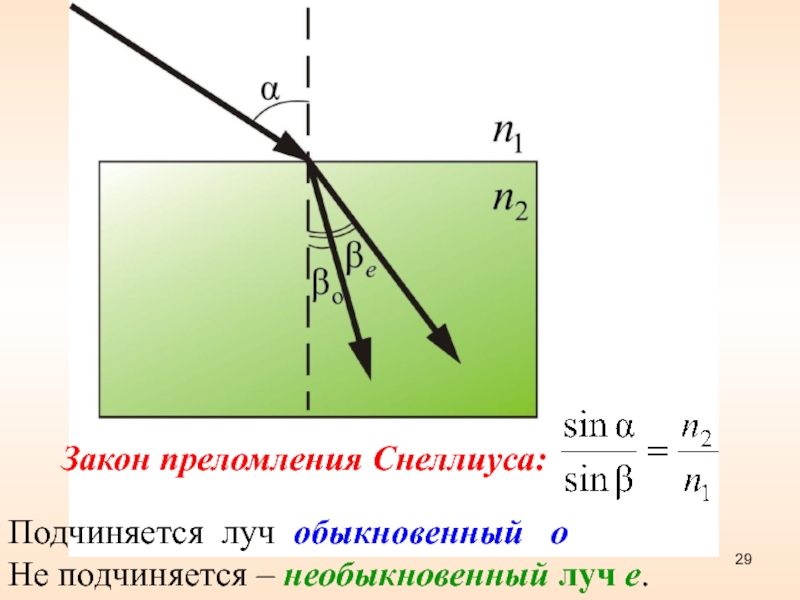
Слайд 29 Закон преломления Снеллиуса:
Подчиняется луч обыкновенный
о
Не подчиняется – необыкновенный луч е.
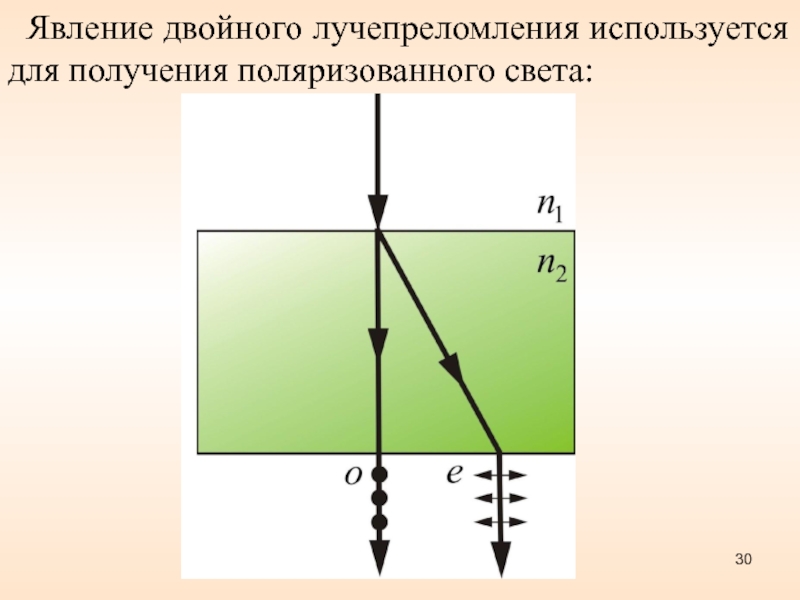
Слайд 30
Рисунок 10.8
Явление двойного лучепреломления используется для получения поляризованного света:
Слайд 32 Дихроизм – один из лучей поглощается сильнее другого
В кристалле турмалина,
обыкновенный луч практически полностью поглощается на длине 1 мм, а
необыкновенный луч выходит из кристалла. В кристалле сульфата йодистого хинина один из лучей поглощается на длине 0,1 мм. Это явление используется для создания поляроидов. На выходе поляроида получается один поляризованный луч.
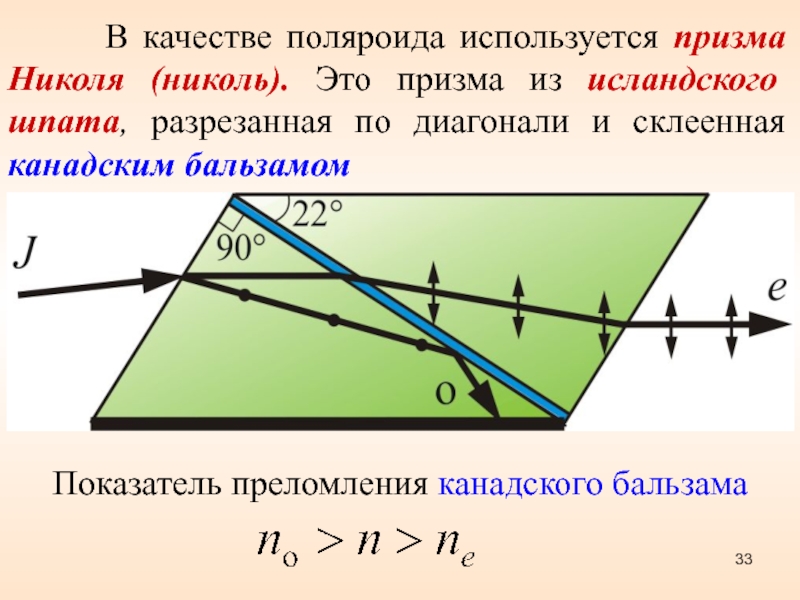
Слайд 33 В качестве поляроида используется призма Николя
(николь). Это призма из исландского шпата, разрезанная по диагонали и
склеенная канадским бальзамомРисунок 10.9
Показатель преломления канадского бальзама
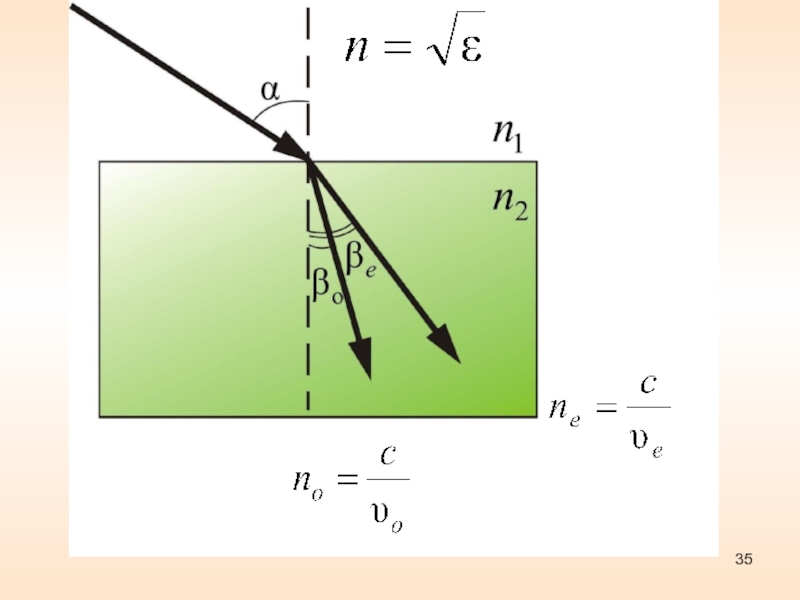
Слайд 34 Двойное лучепреломление объясняется анизотропией кристалла.
Диэлектрическая проницаемость ε – зависит от направления. В одноосных кристаллах
диэлектрическая проницаемость в направлении оптической осии в направлениях перпендикулярных к ней
имеет разные значения.
,
Слайд 36Поскольку
, а в диэлектриках μ = 1, то
Скорость
распространения обыкновенного луча
, а необыкновенного
Показатель преломления обыкновенного луча
и показатель преломлениянеобыкновенного луча
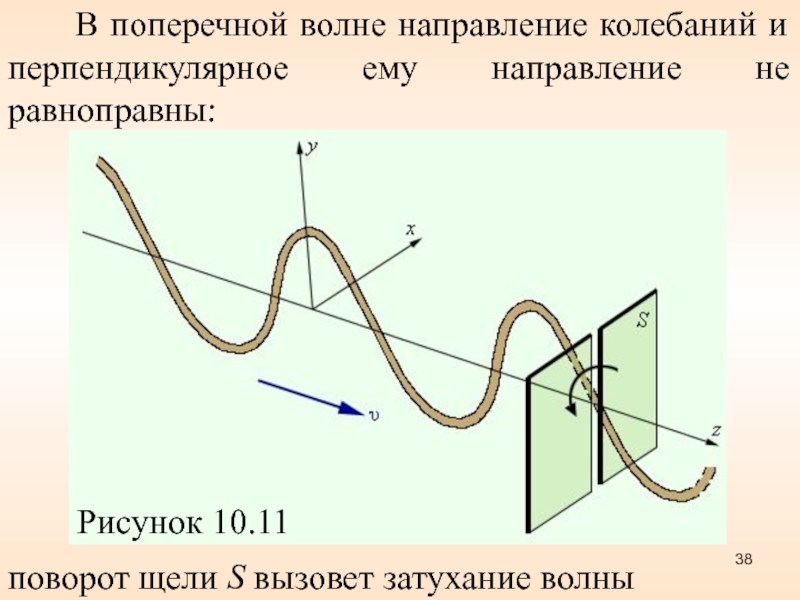
Слайд 38 В поперечной волне направление колебаний и перпендикулярное
ему направление не равноправны:
Рисунок 10.11
поворот щели S вызовет
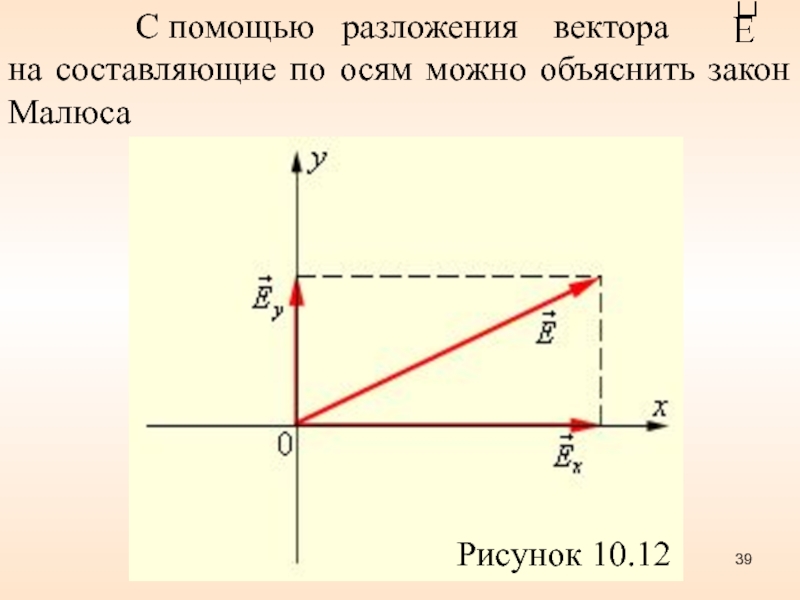
затухание волны Слайд 39 С помощью разложения вектора
на составляющие по осям можно
объяснить закон Малюса
Рисунок 10.12
Слайд 40 Световую волну с амплитудой
разложим на две
составляющие.
–
пройдет через поляризатор, а
– не пройдет.
Т.к
, то
и
Закон Малюса
(10.4.1)
В естественном свете все значения φ равновероятны и среднее значение
Интенсивность естественного света, уменьшается в два раза.
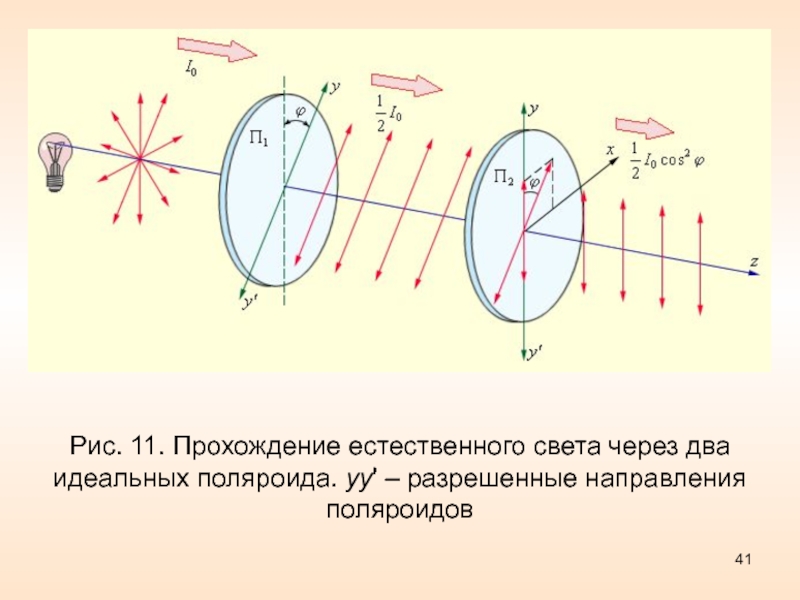
Слайд 41
Рис. 11. Прохождение естественного света через два идеальных поляроида. yy'
– разрешенные направления поляроидов
Слайд 42После первого поляризатора
Второй поляризатор пропустит свет
При φ =
π/2,
, т.е. скрещенные поляризаторы
свет не пропускают
Таким образом,
закон Малюса объясняется на основе разложения вектора Е на составляющие.
при φ = 0.
Слайд 43Прохождение линейно поляризованного света He-Ne лазера через вращающийся поляроид:
Когда направление выделенной оси поляроида совпадает с направлением поляризации падающего
света, на экране за поляроидом видно пятно с максимальной интенсивностью.Когда эти направления перпендикулярны, свет полностью поглощается поляроидом, и световое пятно на экране отсутствует.
Слайд 44Эллипсометрия - изучение поверхностей жидких и твёрдых тел тел по
состоянию поляризации светового пучка, отражённого этой поверхностью и преломлённого на
ней:бесконтактные исследования поверхности жидкости или твёрдых веществ, процессов адсорбции, коррозии…
исследования атомного состава неоднородных и анизотропных поверхностей и плёнок
переход к эллиптической поляризации при отражении и преломлении происходит вследствие наличия тонкого переходного слоя на границе раздела сред.
Источник света – лазер.
Применение плоскополяризованных волн
Две плоскополяризованные волны, падающие на подложку с образцом:
одна волна, отражённая от подложки, остается линейно поляризованной.
вторая меняет поляризацию на круговую.
Слайд 45Микроскопия с использованием принципов эллипсометрии
Излучение лазера (выделено красным) проходит
через поляризатор (отмечено зелёным) и через двулучепреломляющую пластинку (отмечено синим),
которая из волны линейной поляризации формирует эллиптически поляризованную волну.При отражении от образца свет становится линейно поляризованным.
Объектив собирает свет, отражённый от образца и через анализатор (отмечено зелёным) подаёт этот свет на фотоприёмную матрицу.
Анализатор сориентирован так, что задерживает свет линейной поляризации, отражённый от образца, и пропускает значительную часть света эллиптической поляризации, отражённого от подложки.
В результате образец становится видимым на фоне подложки в виде тёмного пятна.
Изменяя взаимную ориентацию поляризатора, анализатора и двулучепреломляющей пластинки, можно получать позитивное и негативное изображение исследуемого объекта.
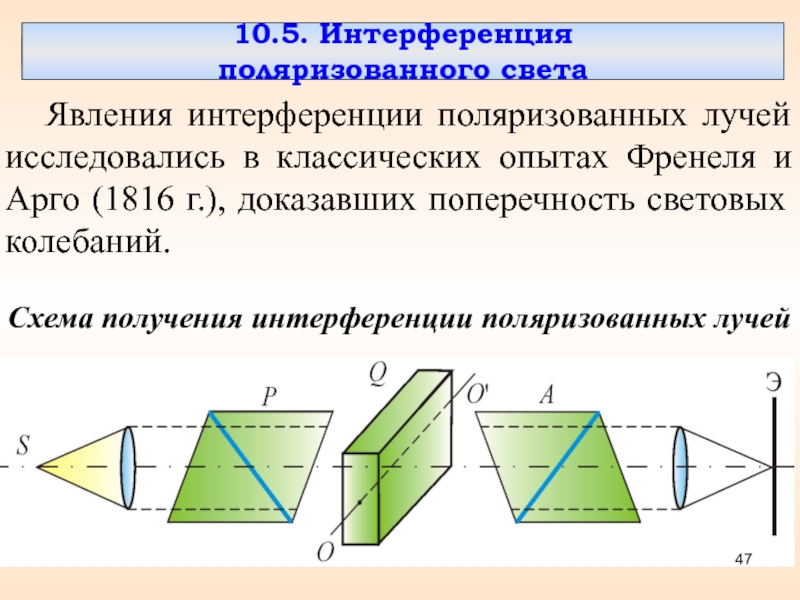
Слайд 4710.5. Интерференция поляризованного света
Явления интерференции поляризованных лучей исследовались в классических
опытах Френеля и Арго (1816 г.), доказавших поперечность световых колебаний.
Схема получения интерференции поляризованных лучей
Слайд 48Араго Доминик Франсуа (26.II.1786 - 2.X.1853) - французский учёный, член
Парижской академии наук (с 1809 года), с 1830 года -
непременный секретарь Парижской АН и директор Парижской обсерватории. Научные работы относятся кастрономии, физике, математике, метеорологии. Автор многих открытий в области оптики и электромагнетизма. По указаниям Араго французские физики И.Физоастрономии, физике, математике, метеорологии. Автор многих открытий в области оптики и электромагнетизма. По указаниям Араго французские физики И.Физо и Ж. Фукоастрономии, физике, математике, метеорологии. Автор многих открытий в области оптики и электромагнетизма. По указаниям Араго французские физики И.Физо и Ж. Фуко экспериментально измерили скорость света, а французский астроном У. Леверьеастрономии, физике, математике, метеорологии. Автор многих открытий в области оптики и электромагнетизма. По указаниям Араго французские физики И.Физо и Ж. Фуко экспериментально измерили скорость света, а французский астроном У. Леверье теоретически, "на кончике пера", открыл планету Нептунастрономии, физике, математике, метеорологии. Автор многих открытий в области оптики и электромагнетизма. По указаниям Араго французские физики И.Физо и Ж. Фуко экспериментально измерили скорость света, а французский астроном У. Леверье теоретически, "на кончике пера", открыл планету Нептун. Араго с 1829 года член Петербургской академии наук.
Слайд 49 Анализатор А здесь необходим также, для того чтобы свести колебания
двух различно поляризованных лучей в одну плоскость.
Разность хода между
двумя компонентами поляризации зависит от толщины пластинки, среднего угла преломления и разности показателей no и ne. Разность фаз:
(10.5.1)
Интенсивность на выходе при скрещенных поляризаторе и анализаторе.
(10.5.2)
Слайд 5010.6. Искусственная анизотропия
Двойное лучепреломление можно наблюдать
в изотропных средах (аморфных телах), если подвергнуть их механическим нагрузкам.
Явление,
открытое в 1818 г. Брюстером, получило название фотоупругости или пьезооптического эффекта.
Обозначим напряжение
От этого напряжения будет зависеть разность показателей преломления:
Слайд 51 Поместим стеклянную пластинку Q между двумя поляризаторами Р
и А :
Рисунок 10.14
В отсутствие механической деформации свет через них
проходить не будет. Если же стекло подвергнуть деформации, то свет может пройти, причем картина на экране получится цветная.
По распределению цветных полос можно судить о распределении напряжений в стеклянной пластинке.
Слайд 52 Помещая прозрачные фотоупругие модели между поляризатором и
анализатором и подвергая их различным нагрузкам, можно изучать распределения возникающих
внутренних напряжений.Слайд 53 Явление искусственной анизотропии может возникать в
изотропных средах под воздействием электрического поля (эффект Керра).
Ячейка Керра:Свет, прошедший через кювету, поворачивает плоскость поляризации, и система становится прозрачной.
Ячейка Керра может служить затвором света, который управляется потенциалом одного из электродов конденсатора, помещенного в ячейку.
Слайд 54 На основе ячеек Керра построены практически
безинерционные затворы и модуляторы света с временем срабатывания до 10−12
с.Величина двойного лучепреломления прямо пропорциональна квадрату напряжённости электрического поля:
Здесь n − показатель преломления вещества в отсутствии поля,
(закон Керра).
k − постоянная Керра.
,где ne и no−показатели преломления для необыкновенной и обыкновенной волн,
Слайд 5510.7. Вращение плоскости поляризации
Оптически активные вещества –
среды, которые
при прохождении через них плоскополяризованного света способны вращать его плоскость
поляризации.Выделяют 2 типа оптически активных веществ:
оптически активные в любом агрегатном состоянии (сахара, камфора, винная кислота): оптическая активность обусловлена асимметричным строением их молекул,
оптически активны только в кристаллической фазе (кварц, киноварь); оптическая активность обусловлена специфической ориентацией молекул (ионов) в элементарных ячейках кристалла.
Оптически активные вещества существуют в 2 формах:
(в зависимости от направления вращения плоскости поляризации) - правой и левой; при этом молекула или кристалл правой формы зеркально-симметричны молекуле или кристаллу левой формы.
Направление вращения:
«+» - вправо относительно наблюдателя, к которому свет приближается;
«-» - влево относительно данного наблюдателя.
Слайд 56В кристаллах:
(сильнее всего вращают плоскость поляризации, если луч распространяется вдоль
оптической оси).
φ – угол поворота;
l – расстояние, пройденное лучом в
кристалле;α – постоянная вращения (зависит от длины волны).
В растворах:
с – концентрация активного вещества;
[α] – удельная постоянная вращения.