Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники
Содержание
- 1. Многогранники
- 2. 7 МногогранникиМногогранниками называются тела, ограниченные плоскими n-угольниками,
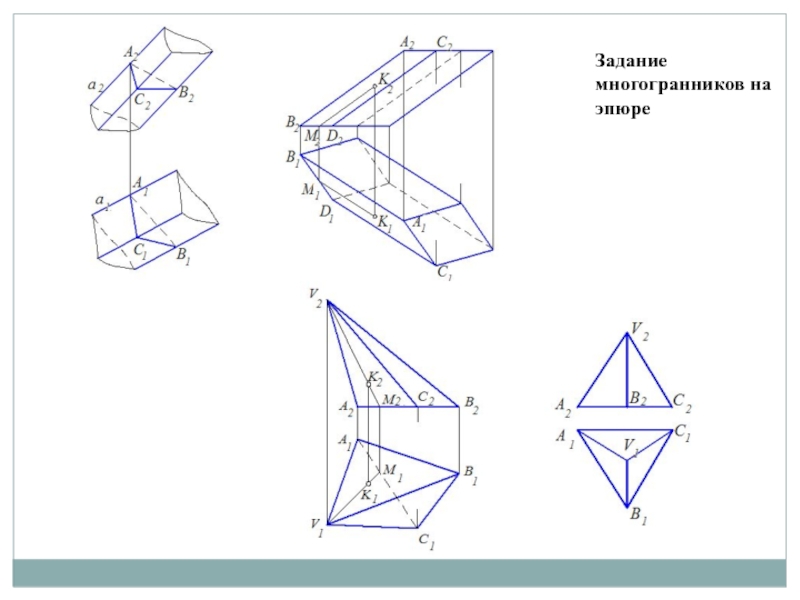
- 3. Задание многогранников на эпюре
- 4. 7.1 Пересечение многогранников плоскостью Для
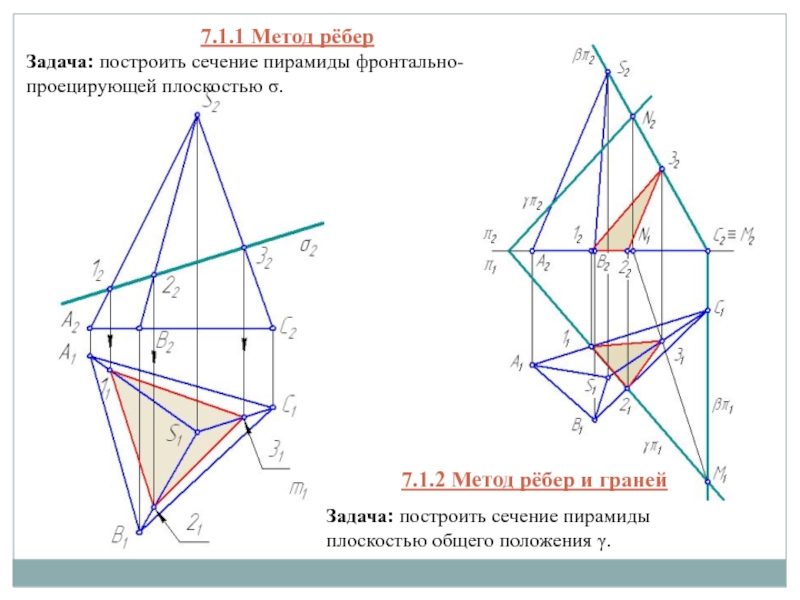
- 5. 7.1.2 Метод рёбер и граней7.1.1 Метод рёберЗадача:
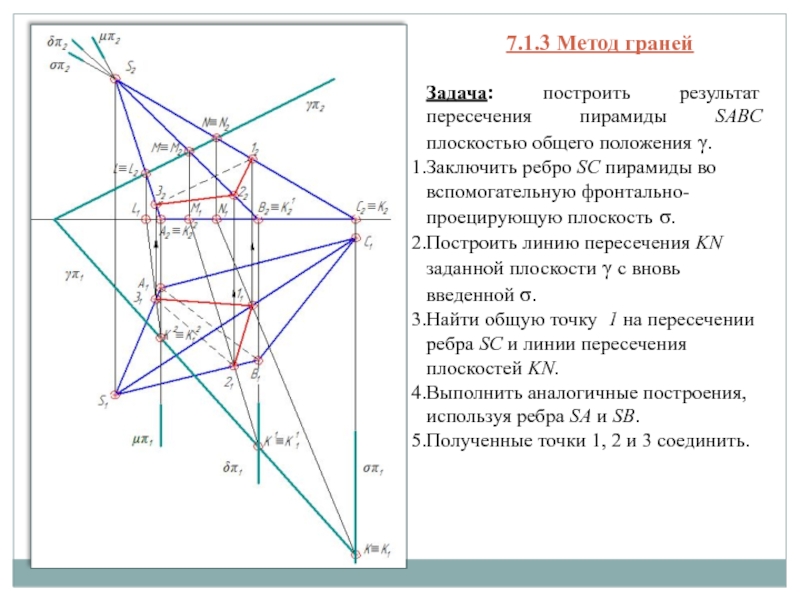
- 6. 7.1.3 Метод гранейЗадача: построить результат пересечения пирамиды
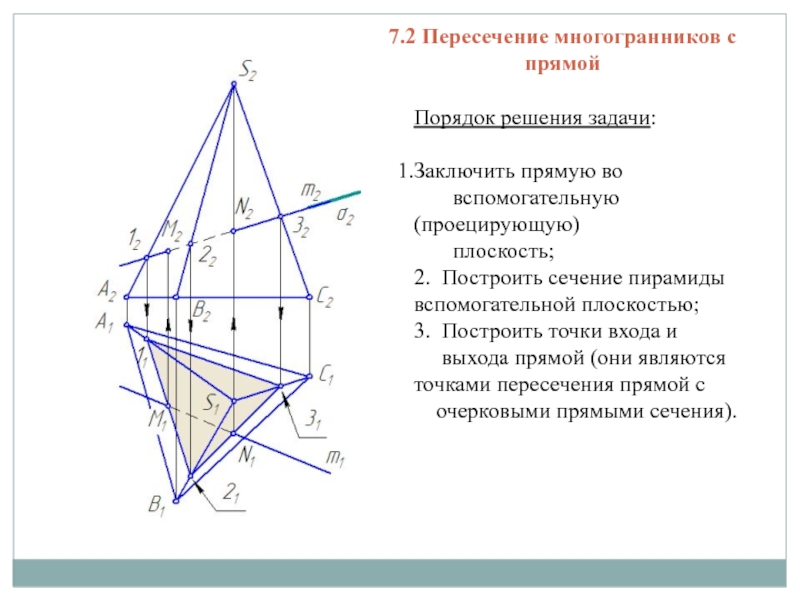
- 7. 7.2 Пересечение многогранников с прямойПорядок решения задачи:Заключить
- 8. 7.3 Построение развёрток поверхностейРазвертка поверхности – фигура,
- 9. 7.3.1 Развёртка поверхности пирамиды методом треугольниковОпределить натуральные
- 10. Слайд 10
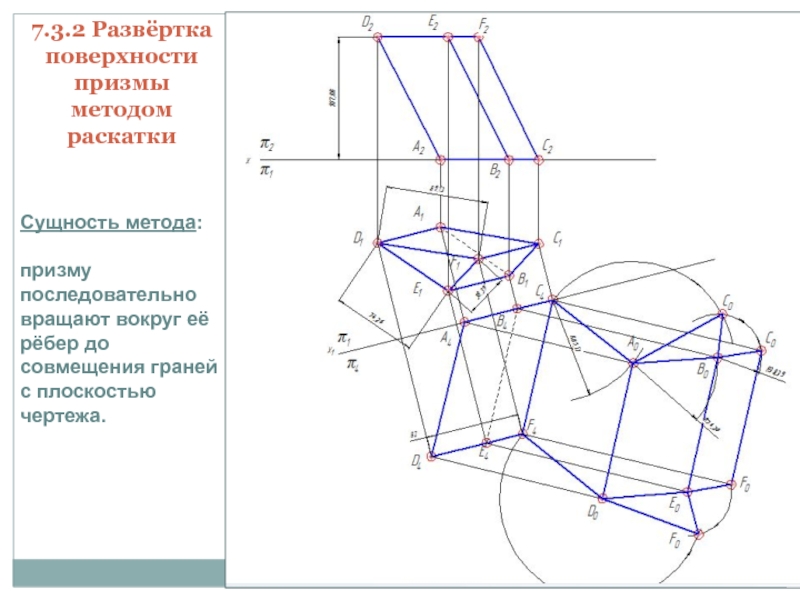
- 11. 7.3.2 Развертка поверхности призмы
- 12. 4. На свободном месте чертежа развернуть контур
- 13. 7.3.2 Развёртка поверхности призмы методом раскаткиСущность метода:
- 14. Скачать презентанцию
7 МногогранникиМногогранниками называются тела, ограниченные плоскими n-угольниками, которые называются гранями. Линии пересечения граней называются ребрами, точки пересечения ребер – вершинами. Для всех многогранников справедлива формула Эйлера: сумма граней и вершин за
Слайды и текст этой презентации
Слайд 1
ЛЕКЦИЯ 7
7.1 ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ ПЛОСКОСТЬЮ
7.2 ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ С ПРЯМОЙ
7.3 ПОСТРОЕНИЕ
РАЗВЁРТОК ПОВЕРХНОСТЕЙ
Слайд 27 Многогранники
Многогранниками называются тела, ограниченные плоскими n-угольниками, которые называются гранями.
Линии пересечения граней называются ребрами, точки пересечения ребер – вершинами.
Для всех многогранников справедлива формула Эйлера: сумма граней и вершин за минусом числа ребер есть величина постоянная: Г + В – Р = 2.
Тетраэдр – это четырехгранник, все грани которого равносторонние треугольники.
Гексаэдр (куб) – шестигранник, все грани которого квадраты.
Октаэдр – восьмигранник, все грани которого равносторонние треугольники.
Додекаэдр – двенадцатигранник, все грани которого правильные пятиугольники.
Икосаэдр – двадцатигранник, все грани которого равносторонние треугольники.
Слайд 47.1 Пересечение многогранников плоскостью
Для построения фигуры сечения
многогранника плоскостью следует:
Определить вершины сечения, как точки пересечения ребер многогранника
с секущей плоскостью (способ ребер);или
построить стороны сечения, как линии пересечения с секущей плоскостью граней многогранника (способ граней).
Чаще применяется первый из заданных приемов, второй – следует применять в тех случаях, когда грани многогранника являются проецирующими плоскостями, линии пересечения которых с секущей плоскостью общего положения строятся очень просто.
Слайд 57.1.2 Метод рёбер и граней
7.1.1 Метод рёбер
Задача: построить сечение пирамиды
фронтально- проецирующей плоскостью σ.
Задача: построить сечение пирамиды плоскостью общего положения
γ.Слайд 67.1.3 Метод граней
Задача: построить результат пересечения пирамиды SABC плоскостью общего
положения γ.
Заключить ребро SC пирамиды во вспомогательную фронтально-проецирующую плоскость σ.
Построить
линию пересечения KN заданной плоскости γ с вновь введенной σ.Найти общую точку 1 на пересечении ребра SC и линии пересечения плоскостей KN.
Выполнить аналогичные построения, используя ребра SA и SB.
Полученные точки 1, 2 и 3 соединить.
Слайд 77.2 Пересечение многогранников с прямой
Порядок решения задачи:
Заключить прямую во
вспомогательную (проецирующую)
плоскость;
2. Построить
сечение пирамиды вспомогательной плоскостью;3. Построить точки входа и
выхода прямой (они являются точками пересечения прямой с
очерковыми прямыми сечения).
Слайд 87.3 Построение развёрток поверхностей
Развертка поверхности – фигура, получаемая совмещением поверхности
геометрического тела с плоскостью чертежа.
Поверхности могут быть развертываемыми и неразвертываемыми.
Развертываемой
называется поверхность, которая при совмещении с плоскостью чертежа не претерпевает изменений: все многогранные поверхности, некоторые линейчатые (конус, цилиндр).Неразвертываемой называется поверхность, которая при совмещении с плоскостью чертежа имеет искажения: нелинейчатые поверхности (сфера, эллипсоид).
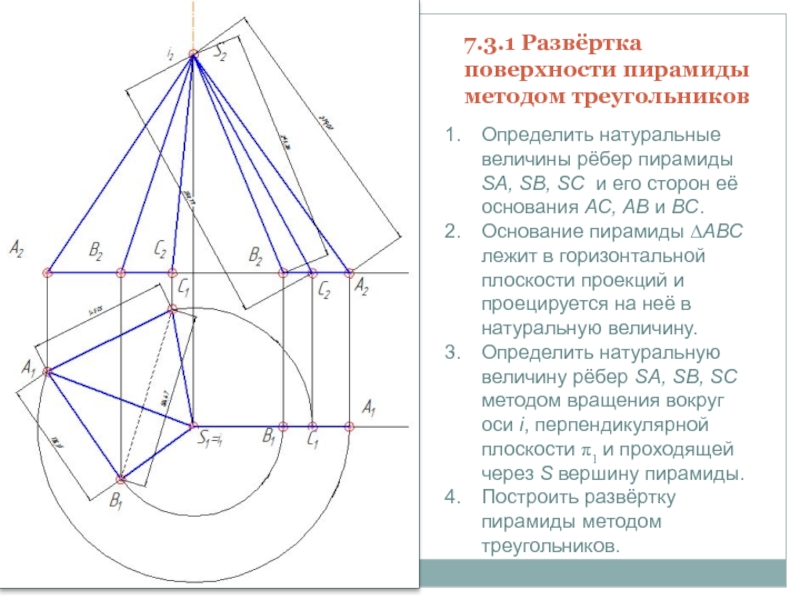
Слайд 97.3.1 Развёртка поверхности пирамиды методом треугольников
Определить натуральные величины рёбер пирамиды
SA, SB, SC и его сторон её основания АС, АВ
и ВС.Основание пирамиды ∆АВС лежит в горизонтальной плоскости проекций и проецируется на неё в натуральную величину.
Определить натуральную величину рёбер SA, SB, SC методом вращения вокруг оси i, перпендикулярной плоскости π1 и проходящей через S вершину пирамиды.
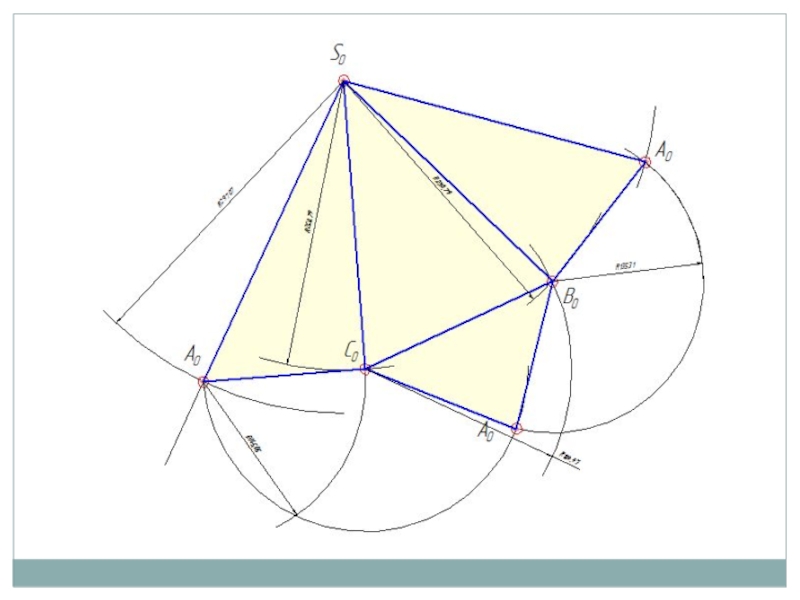
Построить развёртку пирамиды методом треугольников.
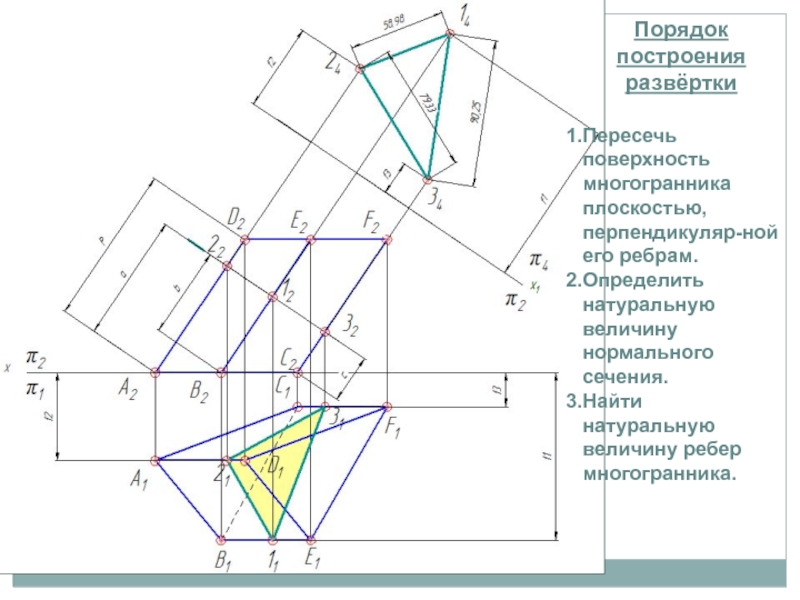
Слайд 117.3.2 Развертка поверхности призмы
методом
нормального сечения
Порядок построения развёртки
Пересечь поверхность многогранника плоскостью, перпендикуляр-ной его ребрам.
Определить
натуральную величину нормального сечения.Найти натуральную величину ребер многогранника.
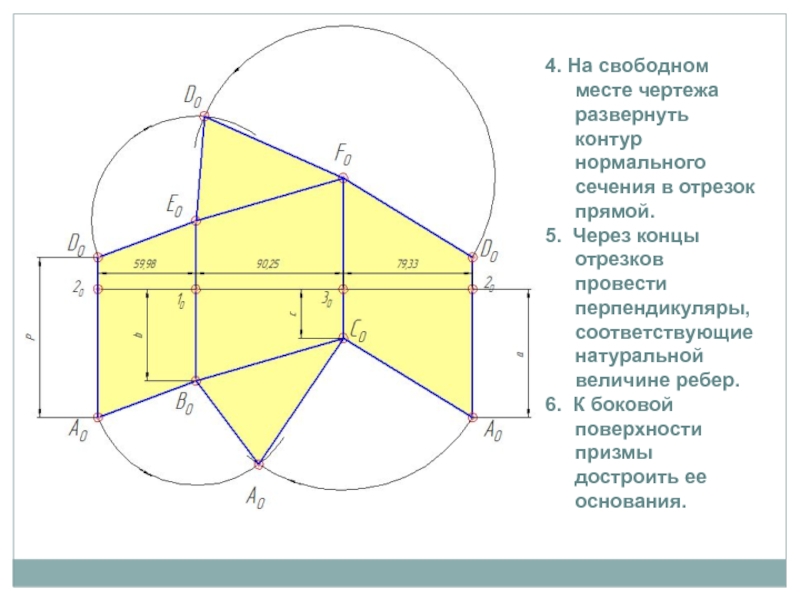
Слайд 124. На свободном месте чертежа развернуть контур нормального сечения в
отрезок прямой.
5. Через концы отрезков провести перпендикуляры, соответствующие натуральной величине
ребер.6. К боковой поверхности призмы достроить ее основания.