Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дисперсия
Содержание
- 1. Дисперсия
- 2. Голография представляет собой одно из многочисленных применений
- 3. Еще одна замечательная особенность голограммы состоит в
- 4. Несмотря на то, что ни одна из
- 5. Принцип голографии представляет собой наглядную иллюстрацию волновой
- 6. Рассмотрим элементарные основы принципа голографии, т. е.
- 7. Идея голографирования состоит в том, что фото-графируется
- 8. Если пленку проявить и осветить аналогичным световым
- 9. Дисперсией света называется зависимость показатель преломления n
- 10. ААα1α2β1β2φРис. 9.1
- 11. Слайд 11
- 12. Из выражения (9.1.4) вытекает, что угол отклонения
- 13. 2) Составные цвета в дифракционном и призматических
- 14. белый
- 15. D=d φ/d λ по модулю так же
- 16. Итак: дисперсией света называется зависимость показателя преломления
- 17. Дисперсия называется аномальной, если dν/dλ0 ,т.е. с
- 18. Слайд 18
- 19. Этот результат не противоречит специальной теории относительности.
- 20. Дисперсия света является результатом взаимодействия электромагнитной волны
- 21. При сложении этих волн они интерферируют, в
- 22. Все это общие качественные положения. Мы рассмотрим
- 23. Подставим выражение для ε в формулу (9.3.1)
- 24. В случае линейно поляризованного монохроматического света с
- 25. Конечно, реально β ≠ 0. Кроме того,
- 26. В результате поглощения интенсивность света при прохождении
- 27. освещении белым светом будет казаться красным. Если
- 28. В 1934 году Л.А. Черенков, аспирант С.Н.
- 29. Согласно электромагнитной теории, заряд движущийся равномерно не
- 30. которые интерферируют друг с другом. При движении заряженной частицы в изотропной среде со скоростью U
- 31. движущийся равномерно и прямолинейно со скоростью U
- 32. Разработанные Черенковым счетчики для регистрации частиц с
- 33. Слайд 33
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 19.1. Голография
9.2. Дисперсия света.
9.3. Нормальная и аномальная дисперсия.
9.4. Элементарная теория
дисперсии (классическая).
ЛЕКЦИЯ 9
Тема: ДИСПЕРСИЯСлайд 2Голография представляет собой одно из многочисленных применений лазера. В своем
обычном виде голограмма выглядит наподобие фотографического негатива.
Однако негатив этот обладает одним замечательным свойством. Хотя он сам по себе является плоским, но если его рассматривать в монохроматическом свете, то мы увидим парящее в пространстве перед или за негативом полное трехмерное изображение реального предмета.
По сравнению со стереоскопическим голографическое изображение имеет ряд преимуществ. В какую бы сторону мы ни перемещались, разглядывая голограмму, в наше поле зрения будет попадать соответствующая часть изображения, как если бы мы разглядывали реальный предмет.
9.1 Голография.
Слайд 3Еще одна замечательная особенность голограммы состоит в том, что изображение
на негативе совершенно не похоже на предмет, который виден парящим
в пространстве.Негатив скорее похож на множество перекрывающихся друг с другом отпечатков пальцев, как на рис. 9.9
Рис. 9.1.
Участок голографического негатива
Слайд 4Несмотря на то, что ни одна из частей негатива не
повторяется где-либо в другом месте, любой из его участков, помещенный
в пучок монохроматического света, воспроизведет трехмерное изображение. Ни при экспозиции негатива, ни при воспроизведении трехмерного изображения не используются линзы, рис. 9.2.Рис. 9.2. Голографический негатив, освещенный монохроматическим светом, дает полное трехмерное изображение, парящее в пространстве
Слайд 5Принцип голографии представляет собой наглядную иллюстрацию волновой природы света и
того, в чем состоит отличие когерентного света от некогерентного.
Чтобы получить
голографический негатив (голограмму), предмет освещается пучком от когерентного источника света – обычно от лазера. При этом на пленку попадает отраженный предметом свет.
Если падающий на фотографическую пленку свет когерентен, то на ней возникает определенная интерференционная картина. Если же свет некогерентен, то пленка засвечивается равномерно.
Слайд 6Рассмотрим элементарные основы принципа голографии, т. е. регистрации и восстановления
информации о предмете. Для регистрации и восстановления волны необходимо уметь
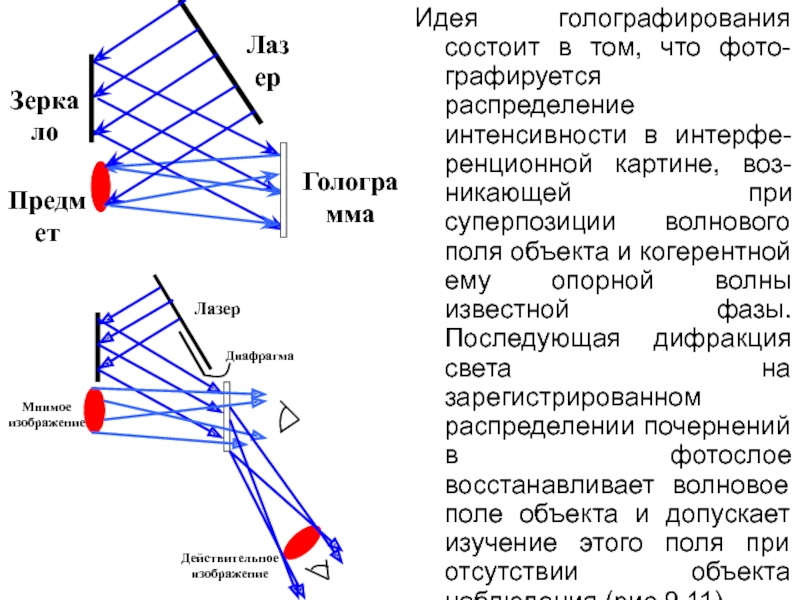
регистрировать и восстанавливать амплитуду и фазу идущей от предмета волны. Это в принципе возможно, так как распределение интенсивности в интерференционной картине, описываемой формулой А2 = А21 + А22 + 2А1А2 cos(α2 – α1) (учитывая, что I ~ А2), определяется как амплитудой интерферирующих волн, так и разностью их фаз. Поэтому для регистрации как фазовой, так и амплитудной информации кроме волны, идущей от предмета (так называемой предметной волны), используют еще когерентную с ней волну, идущую от источника света (так называемую опорную волну).Слайд 7Идея голографирования состоит в том, что фото-графируется распределение интенсивности в
интерфе-ренционной картине, воз-никающей при суперпозиции волнового поля объекта и когерентной
ему опорной волны известной фазы. Последующая дифракция света на зарегистрированном распределении почернений в фотослое восстанавливает волновое поле объекта и допускает изучение этого поля при отсутствии объекта наблюдения (рис.9.11).Лазер
Зеркало
Голограмма
Предмет
Лазер
Мнимое
изображение
Действительное
изображение
Диафрагма
Слайд 8Если пленку проявить и осветить аналогичным световым пучком, то восстановится
и первоначальный волновой фронт в месте расположения пленки в момент
ее экспозиции.Вследствие принципа Гюйгенса восстановленный фронт волны будет перемещаться в направлении глаза наблюдателя точно так же, как это происходило бы с фронтом исходной волны.
Слайд 9Дисперсией света называется зависимость показатель преломления n вещества от частоты
ν (длинны волны λ) света или зависимость фазовой скорости
υ света в среде от его частоты от ν.Дисперсия света представляется в виде зависимости
n=f(λ) (9.1.1)
Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму. Первые систематические экспериментальные наблюдения дисперсии света принадлежат И. Ньютону (1672 г).
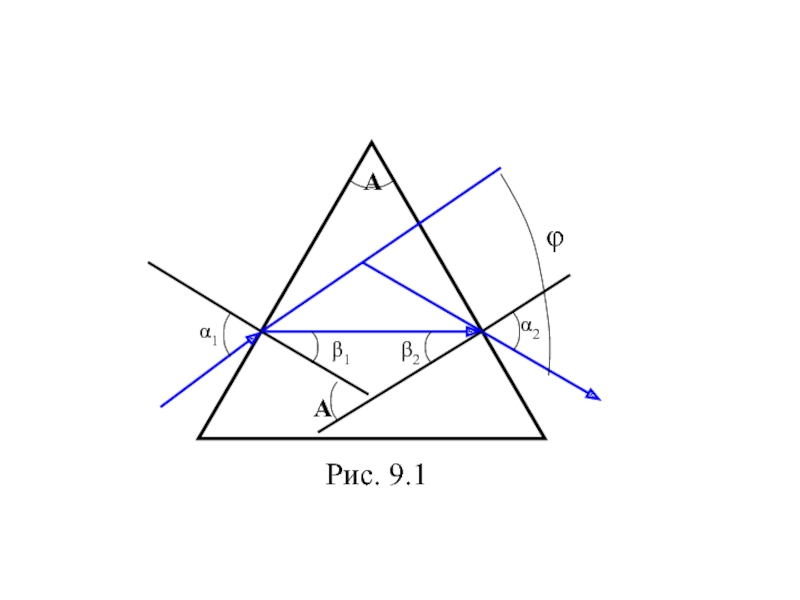
Рассмотрим дисперсию света в призме. Пусть монохроматический пучок света падает на призму с преломляющим углом А и показателем преломления n (рис.9.1) под углом α1. После двукратного преломления (на левой и правой гранях призмы) луч оказывается отклоненным от первоначального направления на угол φ. Из рисунка следует, что
9.2 Дисперсия света.
Слайд 11 φ=(α1-β1)+(α2-β2)=
α1+α2-A (9.1.2)
Предположим, что углы А и α1 малы,
тогда углы будут также малы и вместо синусов этих углов можно воспользоваться их значениями. Поэтому
α1/β1=n , β2/α2=1/n , а т.к. β1 +β2=A1 ,
то
α2=β2=n(A- β1)=n(A- α1/n )=nA- α1
α1+α2=nA (9.1.3)
Из выражения (9.1.2) и (9.1.3) следует, что
φ=A(n-1) (9.1.4)
т.е. угол отклонения лучей призмой тем больше, чем больше преломляющий угол призмы.
Слайд 12Из выражения (9.1.4) вытекает, что угол отклонения лучей призмой зависит
от величины (n – 1), а n - функция длины
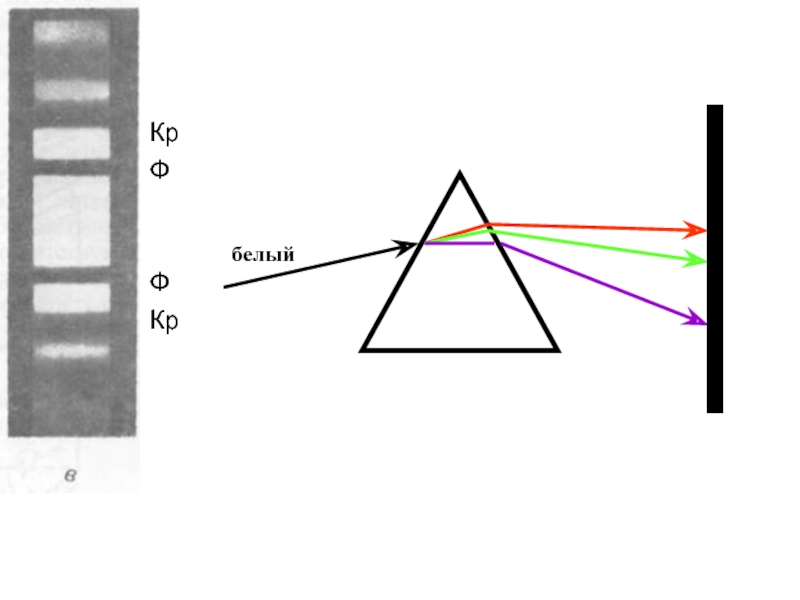
волны , поэтому лучи разных длин волн после прохождения призмы получаются отклоненными на разные углы, т.е. пучок белого света за призмой разлагается в спектр, что и наблюдал Ньютон. Таким образом, с помощью призмы, так же как и с помощью дифракционной решетки, разлагая свет в спектр, можно определить его спектральный состав.Рассмотрим различия в дифракционном и призматическом спектрах.
1) Дифракционная решетка разлагает свет непосредственно по длинам волн, поэтому по измеренным углам (по направлениям соответствующих максимумов) можно вычислить длину волны. Разложение света в спектр в призме происходит по значениям показателя преломления, поэтому для определения длины волны света надо знать зависимость n=f(λ)
Слайд 132) Составные цвета в дифракционном и призматических спектрах располагаются различно.
Мы знаем, что синус угла в дифракционной решетке пропорционален длине
волны. dsinφ=2m.λ/2. Следовательно красные лучи, имеющие большую длину волны, чем фиолетовые, отклоняются дифракционной решеткой сильнее. Призма же разлагает лучи света в спектр по значениям показателя преломления, который для всех прозрачных веществ с увеличением длины волны уменьшается (рис. 9.2). Следовательно, красные лучи, имеющие меньший показатель преломления, чем фиолетовые, отклоняются призмой слабее. Величина D=d φ/d λ, называемая дисперсией, показывает, как быстро меняется показатель преломления с длинной волны. Из рисунка 9.2 следует, что показатель преломления для прозрачных веществ с уменьшени-ем длины волны монотонно увеличивается; следовательно, величина
Рис.9.2
n
λ,нм
Слайд 15D=d φ/d λ по модулю так же увеличивается с уменьшением
λ. Такая дисперсия называется нормальной. Как будет показано ниже, ход
кривой n(λ) - кривой дисперсии - вблизи линий и полос поглощения будет иным, а именно n уменьшается с уменьшением λ. Такой ход зависимости n от λ называется аномальной дисперсией.На явлении нормальной дисперсии основано действие призменных спектрографов. Несмотря на их определенные недостатки (например, необходимость градуировки, различная дисперсия в разных участках спектра) при определении спектрального состава света, призменные спектрографы находят широкое применение в спектральном анализе. Это объяcняется тем, что изготовление хороших призм значительно проще, чем изготовление хороших дифракционных решеток. В призменных спектрографах также легче получить большую светосилу.
Слайд 16Итак: дисперсией света называется зависимость показателя преломления вещества от частоты
световой волны ν (или зависимость фазовой скорости света в среде
от его частоты, т.к. v=c/n). Зависимость показателя преломления среды n=f(λ) не линейна и не монотонна. Области значения ν, в которых соответствует нормальной дисперсии света. Нормальная дисперсия наблюдается у веществ, прозрачных для света. Например, обычное стекло прозрачно для видимого света и в этой области частот наблюдается нормальная дисперсия света в стекле.На основе явления нормальной дисперсии основано «разложение» света стеклянной призмой монохроматоров (например УМ-2)который использовался в лабораторной работе.
9.3 Нормальная и аномальная дисперсия
Рис.9.3
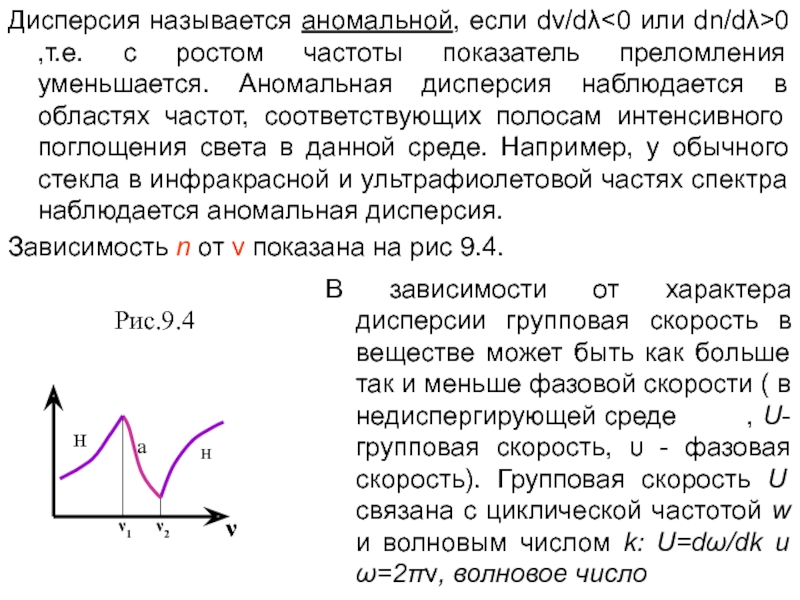
Слайд 17Дисперсия называется аномальной, если dν/dλ0 ,т.е. с ростом
частоты показатель преломления уменьшается. Аномальная дисперсия наблюдается в областях частот,
соответствующих полосам интенсивного поглощения света в данной среде. Например, у обычного стекла в инфракрасной и ультрафиолетовой частях спектра наблюдается аномальная дисперсия.Зависимость n от ν показана на рис 9.4.
В зависимости от характера дисперсии групповая скорость в
веществе может быть как больше так и меньше фазовой скорости ( в
недиспергирующей среде , U-групповая скорость, υ - фазовая скорость). Групповая скорость U связана с циклической частотой w и волновым числом k: U=dω/dk и ω=2πν, волновое число
Рис.9.4
ν1
ν2
ν
н
а
н
Слайд 18 k=
2π/λ= 2πν/c, dω=2πdν,
dk= 2π/c(ndν+(dν/dn)dν)-полный дифференциал от ω и k. Отсюда:
Можно записать:
При нормальной дисперсии U<ν, а значит U
При аномальной дисперсии U>ν и, в частности, если
Слайд 19Этот результат не противоречит специальной теории относительности. Понятие групповой скорости
правильно описывает распространение только такого сигнала ( волнового пакета ),
форма которого не изменяется при перемещении сигнала в среде. (Строго говоря это условие выполняется только для вакуума, т.е. в недиспергирующей среде). В области частот, соответствующих аномальной дисперсии групповая скорость не совпадает со скоростью сигнала, т.к. в следствие значительной дисперсии форма сигнала так быстро изменяется, что не имеет смысла говорить о групповой скорости.то
Слайд 20Дисперсия света является результатом взаимодействия электромагнитной волны с заряженными частицами,
входящими в состав вещества. Теория Максвелла не могла объяснить это
явление так как Максвелл не знал о сложном строении атома. Классическая теория была разработана Х.А. Лоренцом лишь после создания им же электронной теории строения вещества. Он показал, что, а ε – тоже зависит от частоты. Для видимого света существует только поляризация электрически упругого смещения. Смещаются в основном валентные электроны. В процессе вынужденных (под действием падающей световой волны ) колебания электронов с частотой ν (частота вынуждающей силы) переодически изменяются дипольные электрические моменты атомов. Следовательно, частота которых тоже ν. Среднее расстояние между атомами вещества много меньше протяженности одного цуга волн, следовательно, вторичные волны, излучаемые большим числом соседних атомов, когерентны, как между собой, так и с первичной волной.9.4 Элементарная теория дисперсии (классическая)
Слайд 21При сложении этих волн они интерферируют, в результате этой интерференции
и получаются все наблюдаемые оптические явления связанные с взаимодействием света
с веществом. Фаза вторичной волны другая (сказывается запаздывание смещения электрона – смещение происходит только при достижении определенной величены электрического поля), но разность фаз первичной и вторичной волн, постоянна. Скорость распространения фронта волны (фазовая скорость ) зависит от результата сложения, т.е. от фазы результирующей волны.В однородном изотропном веществе в результате интерференции образуется проходящая волна, направление распространения которой совпадает с направлением первичной волны.
В оптически неоднородной среде (с разным n ) сложение первой и второй волн приводит к рассеянию света.
При падении света на границу раздела двух сред в результате интерференции возникает не только проходящая (преломленная), но и отраженная волна. Отражение происходит не от геометрической поверхности раздела, а от более или менее значительного слоя частиц среды, прилегающих к границе раздела.
Слайд 22Все это общие качественные положения. Мы рассмотрим только элементарную теорию
дисперсии в однородном изотропном диэлектрике.
Наша цель - найти зависимость n=n(w)
, а т.к n=√ ε (9.3.1)
то найдем вначале зависимость ε=ε(w) , где w –циклическая частота колебаний. Мы знаем, что P=1+χ=1+P/(ε0E),
где Р - вектор поляризации (в данном случае - его проекция на направление внешнего поля E ), χ - диэлектрическая восприимчивость среды. Примем, что, поляризация обусловлена смещением только валентных (оптических) электронов. Для атомов с одним оптическим электроном P=-er (P=ql), тогда
P=pn0=-n0er , где p-дипольный электрический момент атома; n0 - концентрация атомов; q -заряд электрона; r - смещение электрона. Знак (-) учитывает отрицательный заряд электрона.
Слайд 23Подставим выражение для ε в формулу (9.3.1) и найдем n2:
(9.3.2)
Итак, задача сводится к нахождению зависимости смещения r электрона под действием внешнего поля Е. Оптический электрон совершает вынужденные колебания под действием следующих сил:
а) возвращающей квазиупругой силы Fв=-mω02r , где m, w - масса и частота свободных незатухающих колебания электрона;
б) силы сопротивления (со стороны других атомов) Fстор.=-2βm(dr/dt) где β -коэффициент затухания.
в) вынуждающей силы F=-qe ; E –напряженность электрического поля световой волны.
Уравнение вынужденных колебаний
Слайд 24В случае линейно поляризованного монохроматического света с циклической частотой ω
E=E0cosωt, где Е0 - амплитуда. Тогда
. Его решение имеет вид Если среда не поглощает свет, β=0 и
Подставим в (9.3.2) и получим
Атомы вещества колеблются, поэтому внутреннее поле (поле остальных атомов) (рис9.5) непостоянно во времени - картина получается сложной.
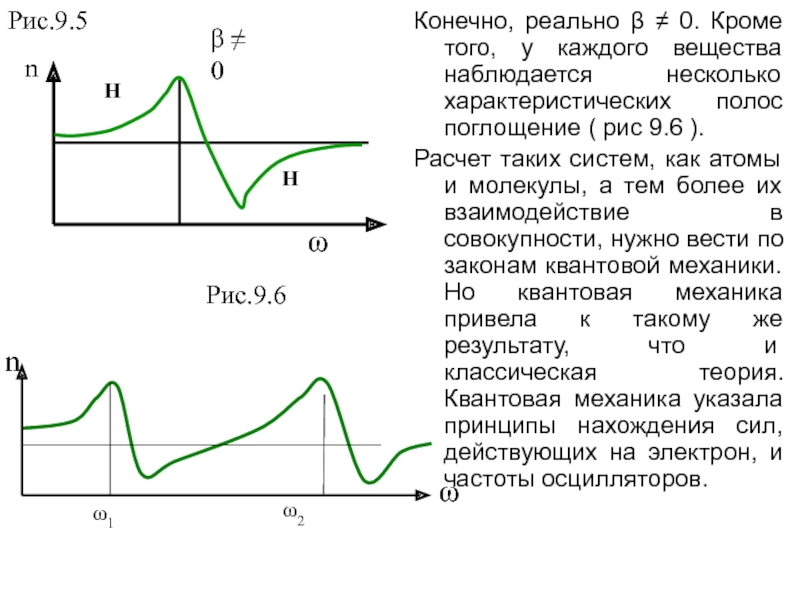
Слайд 25Конечно, реально β ≠ 0. Кроме того, у каждого вещества
наблюдается несколько характеристических полос поглощение ( рис 9.6 ).
Расчет таких
систем, как атомы и молекулы, а тем более их взаимодействие в совокупности, нужно вести по законам квантовой механики. Но квантовая механика привела к такому же результату, что и классическая теория. Квантовая механика указала принципы нахождения сил, действующих на электрон, и частоты осцилляторов.H
H
n
ω
β ≠ 0
ω1
ω2
ω
n
Рис.9.5
Рис.9.6
Слайд 26В результате поглощения интенсивность света при прохождении света через вещество
уменьшается. Закон Бугера (1729 г., французский ученый)
, где - интенсивность плоской монохроматической волны на входе, - коэффициент поглощения (зависит от длины волны, природы и состояния вещества, но не зависит от интенсивности света) . Для одно атомных газов и паров металлов, атомы которых расположены далеко друг от друга (можно их считать изолированными ) лишь в узких спектральных областях наблюдаются резкие максимумы (линейчатые спектры поглощения), соответствующие частотам собственных колебаний электронов в атомах (10-10-10-7). У диэлектриков наблюдается селективное поглощение и сравнительно широкие полосы поглощения (10-7-10-6), т.е. диэлектрики имеют сплошной спектр поглощения.В металлах энергия падающей электромагнитной волны приводит к возникновению быстро переменных токов, сопровождающихся выделением джоулева тепла. Чем выше проводимость металла, тем сильнее в нем поглощается свет. Из рисунка 9.7 видно, что внутри
Слайд 27освещении белым светом будет казаться красным. Если на это стекло
направить синий и зеленый свет, то из-за сильного поглощения этих
длин волн стекло будет казаться черным. Это явление используется для изготовления светофильтров.Разнообразие пределов селективного (избирательного) поглощения у различных веществ объясняет разнообразие и богатство цветов и красок, наблюдающиеся в окружающем нас мире
полосы поглощения наблюдается аномальная дисперсия (n - возрастает с ростом λ ). Зависимостью коэффициента поглощения от длины волны объясняется окрашенность поглощающих тел. Например: стекло слабо поглощающее красные и оранжевые лучи и сильно поглощающее синий и зеленые при
Рис.9.7
α
n
Слайд 28В 1934 году Л.А. Черенков, аспирант С.Н. Вавилова, обнаружил особый
вид свечения жидкости под действием γ-лучей радия. Характерные особенности излучения:
1) свечение имеет голубоватый цвет и наблюдается у всех чистых прозрачных жидкостей, 2)яркость и цвет свечения мало зависят от химического состава жидкости, в отличие от люминесценции не наблюдается ни температурного, ни примесного свечения. Вавилов правильно предположил, что обнаруженное явление - не люминесценция, а свет излучают быстрые электроны, движущиеся в жидкости. В 1937 году И.Е. Тамм и И.М. Франк объяснили механизм свечения и создали количественную теорию, основанную на уравнениях классической электродинамики. (В 1940 году В.Л. Гинзбург создал квантовую теорию, которая привела к тем же результатам).Излучение Вавилова-Черенкова - излучение света, электрически заряженной частицей, движущейся в среде с групповой скоростью u, превышающей фазовую скорость света в этой среде
9.5. Излучение Вавилова-Черенкова.
Слайд 29Согласно электромагнитной теории, заряд движущийся равномерно не излучает электромагнитной волны.
Однако Тамм и Франк показали, что это справедливо лишь для
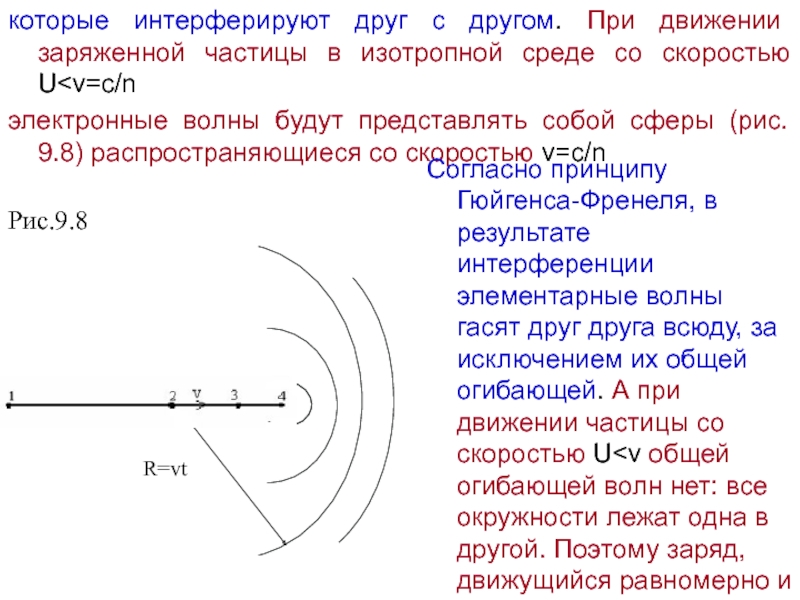
скоростей частиц, не превышающих фазовую скорость волны в данной среде. В процессе излучения Вавилова - Черенкова энергия и скорость излучающей свободной частицы уменьшается, то есть частица тормозится. Однако в отличие от обычного тормозного излучения медленно движущейся заряженной частицы, являющейся следствием изменения ее скорости, уменьшение скорости частицы при излучении Вавилова-Черенкова само является следствием этого излучения. Иными словами, если бы убыль энергии восполнялась, то частица, двигаясь с постоянной скоростью ( U>v), испускала бы излучение Вавилова-Черенкова, а тормозного излучения не было бы. Заряженная частица вызывает кратковременную поляризацию вещества в окрестности тех точек, через которые она проходит при своем движении. Поэтому молекулы среды, лежащие на пути частицы, становятся кратковременно действующими когерентными источниками элементарных электромагнитных волн,Слайд 30которые интерферируют друг с другом. При движении заряженной частицы в
изотропной среде со скоростью U
(рис. 9.8) распространяющиеся со скоростью v=c/nСогласно принципу Гюйгенса-Френеля, в результате интерференции элементарные волны гасят друг друга всюду, за исключением их общей огибающей. А при движении частицы со скоростью U Рис.9.8 R=vt
Слайд 31движущийся равномерно и прямолинейно со скоростью U
частица движется быстрее, чем распространяются волны в среде, то соответствующие
элементарным волнам сферы пересекаются, и их общая огибающая (волновая поверхность) представляет собой конус с вершиной в точке, совпадающей с мгновенным положением движущейся частицы. Нормали к образующим конуса определяют волновые векторы, т.е. направления распространения света. Угол , который составляет волновой вектор с направлением движения частицы, удовлетворяютсоотношению
В жидкостях и твердых телах условие U > v начинает выполнятся для электронов при E>105 эВ, а для протонов E>108 эВ .
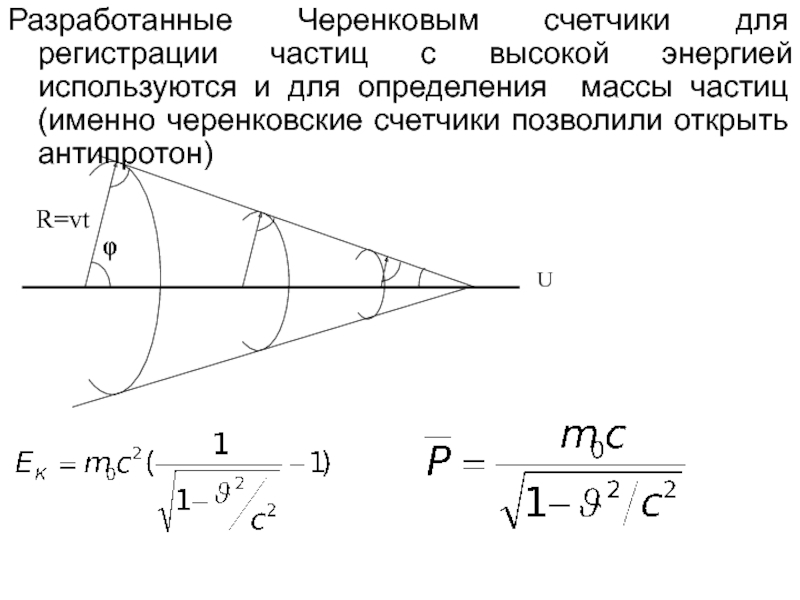
Слайд 32Разработанные Черенковым счетчики для регистрации частиц с высокой энергией используются
и для определения массы частиц (именно черенковские счетчики позволили открыть
антипротон)φ
R=vt
U