Слайд 1NP-полнота
Если мы хотим провести пусть грубую, но формальную границу между
"практическими" алгоритмами и алгоритмами, представляющими лишь теоретический интерес, то класс
алгоритмов, работающих за полиномиальное время, является разумным первым приближением.
Для NP-полных задач не найдены полиномиальные алгоритмы, однако и не доказано, что таких алгоритмов не существует. Изучение NP-полных задач связано с так называемым вопросом P = NP. Это одна из наиболее сложных проблем теории вычислений (1971г.) .
Если для некоторой задачи удается доказать ее NP-полноту, есть основания считать ее практически неразрешимой. В этом случае лучше потратить время на построение приближенного алгоритма, чем продолжать искать быстрый алгоритм, решающий ее точно.
Слайд 2Полиномиальное время
Абстрактные задачи
Понятие полиномиально разрешимой задачи принято считать
уточнением идеи "практически
разрешимой" задачи так как:
используемые на практике полиномиальные алгоритмы обычно действительно
работают довольно быстро;
объем этого класса практически не зависит от выбора конкретной модели вычислений. Например, класс задач, которые могут быть решены за полиномиальное время на МНР, совпадает с классом задач, полиномиально разрешимых на машинах Тьюринга. Класс будет тем же и для модели параллельных вычислений, если число процессоров ограничено полиномом от длины входа.
класс полиномиально разрешимых задач обладает свойствами замкнутости. Например, композиция двух полинолмиальных алгоритмов также работает полиномиальное время, потому, что сумма, произведение и композиция многочленов есть многочлен.
Слайд 3Абстрактная задача – произвольное бинарное отношение Q между элементами двух множеств –
множества условий I и множества решений S.
Например, в задаче
поиска кратчайшего пути между двумя заданными вершинами неориентированного графа G = (V, E) условием (элементом I) является тройка, состоящая из графа и двух вершин, а решением (элементом S) – последовательность вершин, составляющих требуемый путь в графе.
В теории NP-полноты рассматриваются только задачи разрешения – задачи, в которых требуется дать ответ "да" или "нет" на некоторый вопрос. Формально её можно рассматривать как функцию, отображающую множество условий I во множество {0, 1}.
Например, с задачей поиска кратчайшего пути в графе связана задача разрешения: "по заданному графу G = (V, E), паре вершин u, v ∈ V и числу k определить, существует ли в G путь между вершинами u и v, длина которого не превосходит k".
Слайд 4Представление данных
Будем считать, что исходные данные закодированы последовательностью битов. Формально
говоря, представлением элементов некоторого множества S называется отображение e из
S во множество битовых строк. Например, целые числа 0, 1, 2, 3, … обычно представляются битовыми строками 0, 1, 10, 11, 100, …
Фиксировав представление данных, мы превращаем абстрактную задачу в строковую, для которой входными данными является битовая строка, представляющая исходные данные абстрактной задачи. Будем говорить, что алгоритм решает строковую задачу за время O(T(n)), если на входных данных (битовой строке) длины n алгоритм работает время O(T(n)). Строковая задача называется полиномиальной, если существует константа k и алгоритм, решающий эту задачу за время O(nk). Сложностной класс P – множество всех строковых задач разрешения, которые могут быть решены за полиномиальное время, т. е. за время O(nk), где k не зависит от входа.
Слайд 5Для каждого представления e множества I входов абстрактной задачи Q
мы получаем свою строковую задачу. Однако на практике (если исключить
такие "дорогие" способы представления, как система счисления с основанием 1) естественные способы представления оказываются обычно эквивалентными, поскольку они могут быть полиномиально преобразованы друг в друга. Будем говорить, что функция
f : {0,1}* → {0,1}* вычислима за полиномиальное время, если существует полиномиальный алгоритм A, который для любого x ∈ {0,1}* выдает результат f (x).
Рассмотрим множество I условий произвольной абстрактной задачи разрешения. Два представления e1 и e2 этого множества называются полиномиально связанными, если существуют две вычислимые за полиномиальное время функции f1→2 и f2→1, для которых f1→2(e1(i)) = e2(i) и f2→1(e2(i)) = e1(i) для всякого i ∈ I. В этом случае не имеет значения, какое из двух полиномиально связанных представлений выбрать.
Слайд 6Формальные языки
Алфавитом Σ называется любой конечный набор различных символов. Языком
L над алфавитом Σ называется произвольное множество строк символов из
алфавита Σ (такие строки называются словами в алфавите Σ). Например, можно рассмотреть Σ = {0, 1} и язык L = {10, 11, 101, 111, 1011, …}, состоящий из двоичных записей простых чисел. Символ ε пустое слово, не содержащее символов, а символом ∅ – пустой язык, не содержащий слов.
Имеется несколько стандартных операций над языками. Операции объединения и пересечения языков определяются как обычные операции объединения и пересечения множеств. Конкатенацией двух языков L1 и L2 называется язык L = {x1x2 | x1 ∈ L1, x2 ∈ L2} Замыканием языка L называется язык L* = {ε} ∪ L ∪ L2 ∪ L3 ∪ …, где Lk — язык, полученный k-кратной конкатенацией L с самим собой. Операция замыкания называется также *-операцией Клини.
Строковая задача разрешения является языком над алфавитом Σ. Например, задаче разрешения о существовании в графе пути длины не превосходящей k, соответствует язык PATH = { | G = (V, E) — неориентированный граф, u, v ∈ V; k ≥ 0 – число, и в графе G существует путь из u в v, длина которого не превосходит k.}

Слайд 7Алгоритм A допускает слово x ∈ {0,1}*, если на входе x алгоритм
выдает результат 1; если же A выдает 0, говорят, что
он отвергает слово x. Заметим, что алгоритм может не останавливаться на входе x, или дать ответ отличный от 0, 1. В этом случае он и не допускает, и не отвергает слово x. Алгоритм А допускает язык L, если алгоритм допускает те и только те слова, которые принадлежат языку L. Алгоритм А, допускающий некоторый язык L, не обязан отвергать всякое слово x ∉ L.
Если алгоритм A допускает все слова из L, а все остальные отвергает, то говорят, что A распознает язык L.
Язык L допускается за полиномиальное время, если имеется алгоритм A, который допускает данный язык, причем всякое слово x ∈ L допускается алгоритмом за время O(nk), где n – длина слова x, а k – некоторое не зависящее от x число.
Язык L распознается за полиномиальное время, если некоторый алгоритм A распознает данный язык, причем время работы алгоритма на каждом слове длины n не больше O(nk).
Слайд 8Рассмотренный ранее язык PATH, допускается за полиномиальное время.
Нетрудно построить
алгоритм, который методом поиска в ширину за полиномиальное время находит
кратчайший путь между вершинами u и v в графе G, а затем сравнивает длину найденного пути с данным в условии числом k.
Если длина пути не превосходит k, алгоритм выдает 1 и останавливается. В противном случае алгоритм зацикливается, не выдавая никакого ответа.
Такой алгоритм допускает, но не распознает язык PATH. Его можно исправить таким образом, чтобы слова, не принадлежащие языку, отвергались. Такой алгоритм допускает и распознает язык PATH.
Некоторые языки (например, для множества всех программ, заканчивающих свою работу) имеют допускающий алгоритм, но не имеют распознающего.
Определение класса P: P = {L ⊂ {0,1}* | существует алгоритм A, распознающий L за полиномиальное время.}
Слайд 9Теорема
P = {L | L допускается за полиномиальное время}.
Доказательство. Если язык распознается
некоторым алгоритмом, то он и допускается тем же алгоритмом. Остается
доказать, что если язык L допускается полиномиальным алгоритмом A, то он и распознается некоторым (возможно, другим) полиномиальным алгоритмом A′. Пусть алгоритм A допускает язык L за время O(nk). Это значит, что существует константа c, для которой A допускает любое слово длины n из L, сделав не более T = cnk шагов. С другой стороны слова не из L алгоритм не допускает (ни за какое время).
Новый алгоритм A′ моделирует работу алгоритма A и считает число шагов этого алгоритма, сравнивая его с известной границей T. Если за время T алгоритм A допускает слово x, алгоритм A′ также допускает это слово и выдает 1. Если же A не допускает x за указанное время, то алгоритм A′ прекращает моделирование и отвергает слово (выдает 0). Замедление работы за счет моделирования и подсчета шагов не так уж велико и оставляет время работы полиномиальным.
Слайд 10Проверка принадлежности языку и класс NP
Задача разрешения PATH полиномиальной т.к.
решается с помощью алгоритма поиска в ширину. Если поиск в
ширину неизвестен, то задача PATH будет трудноразрешимой: т.к. по графу G, вершинам u и v и числу k, неизвестно, есть ли искомый путь, пока его не покажут. Но если он известен, то можно легко проверить, что этот путь – искомый. Именно такая ситуация имеет место для задач из класса NP.
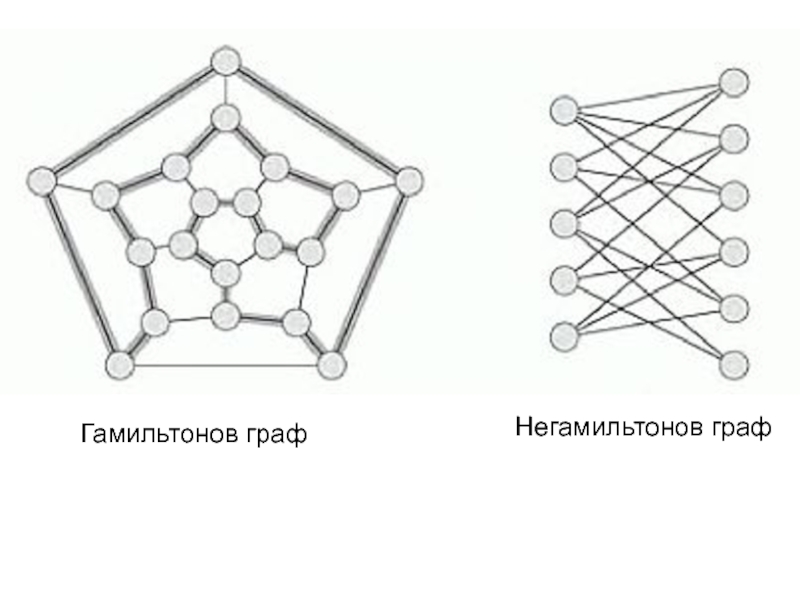
Слайд 11Гамильтонов цикл
Гамильтоновым циклом в неориентированном графе G = (V, E) называется простой цикл,
который проходит через все вершины графа. Графы, в которых есть
гамильтонов цикл, называют гамильтоновыми. Задача о гамильтоновом цикле состоит в выяснении, имеет ли заданный граф G гамильтонов цикл. HAM-CYCLE = { | G – гамильтонов граф}. Задача о гамильтоновом цикле является NP-полной, и поэтому можно предполагать, что полиномиального алгоритма для нее вообще не существует.
Слайд 12Гамильтонов граф
Негамильтонов граф
Слайд 13Проверка принадлежности языку
Определить, является ли граф гамильтоновым, за полиномиальное время,
скорее всего, невозможно, однако доказательство существования гамильтонова цикла в графе
(состоящее в предъявлении гамильтонова пути) можно проверить за полиномиальное время. Проверяющим алгоритмом называется алгоритм A с двумя аргументами; первый аргумент — входная строка, а второй − сертификат. A допускает вход x, если существует сертификат y, для которого A(x, y) = 1. Язык, проверяемый алгоритмом A: L = {x ∈ {0, 1}*: ∃ y ∈ {0,1}*, A(x, y) = 1}. Другими словами, алгоритм A проверяет язык L, если для любой строки x ∈ L найдется сертификат y, с помощью которого A может проверить принадлежность x к языку L, а для x ∉ L такого сертификата нет. Например, в задаче HAM-CYCLE сертификатом была последовательность вершин, образующая гамильтонов цикл.
Слайд 14Теорема Кука
Задача выполнимости булевых формул (SAT или ВЫП) или
Задача
распознавания
Экземпляром задачи SAT является булева формула, состоящая только из имен
переменных, скобок и операций ∧, ∨ и ¬.
Задача заключается в следующем: можно ли назначить всем переменным, встречающимся в формуле, значения ЛОЖЬ и ИСТИНА так, чтобы формула стала истинной.
Согласно теореме Кука, доказанной Стивеном Куком в 1971 году, задача SAT NP-полна.
Слайд 15Условимся об алфавите, с помощью которого задаются экземпляры языка. Этот
алфавит должен быть фиксирован и конечен. Будем использовать следующий алфавит:
{∨, ∧, ¬, (, ), x, 0, 1}.
При использовании такого алфавита скобки и операторы записываются естественным образом, а переменные получают следующие имена: x1, x10, x11, x100 и т. д., согласно их номерам, записанным в двоичной системе счисления
Пусть некоторая булева формула, записанная в обычной математической нотации, имела длину N символов. В ней каждое вхождение каждой переменной было описано хотя бы одним символом, следовательно, всего в данной формуле не более N переменных. Значит, в предложенной выше нотации каждая переменная будет записана с помощью O (log N )символов. В таком случае, вся формула в новой нотации будет иметь длину O ( N log N ) символов, то есть длина строки возрастет в полиномиальное число раз.
Слайд 16В 1971-м году в статье Стивена Кука был впервые введен
термин «NP-полная задача», и задача SAT была первой задачей, для
которой доказывалось это свойство.
В доказательстве теоремы Кука каждая задача из класса NP в явном виде сводится к SAT. После появления результатов Кука была доказана NP-полнота для множества других задач. При этом чаще всего для доказательства NP-полноты некоторой задачи полиномиальноесведение задачи SAT к данной задаче, возможно в несколько шагов, то есть с использованием нескольких промежуточных задач.
Слайд 17КЛАССЫ СЛОЖНОСТИ
Целесообразно определить сложность задачи - например, как сложность самого
эффективного алгоритма, решающего эту задачу (для данных размера n). К
сожалению, это невозможно. Доказано, что есть
задачи, для которых не существует самого быстрого алгоритма, потому что любой алгоритм для такой задачи можно «ускорить», построив более быстрый алгоритм, решающий эту задачу. Это утверждение называется теоремой Блюма об ускорении. Упрощенный вариант теоремы Блюма таков:
Слайд 18ТЕОРЕМА (теорема Блюма об ускорении). Существует такая алгоритмически разрешимая задача
Z, что любой алгоритм A,решающий задачу Z, можно ускорить следующим
образом:
существует другой алгоритм A′, также решающий Z и такой, что TA′(n) ≤ log TA(n) для почти всех n.
Теорема Блюма не утверждает, что ускорение возможно для любой задачи. Более того, интересных с практической точки зрения, ускорение невозможно; для таких задач существует оптимальный (самый быстрый) алгоритм. Тем не менее, утверждение теоремы Блюма о существовании «неудобных» задач не позволяет определить универсальное (применимое ко всем задачам) понятие «оптимального алгоритма».