Гипербола

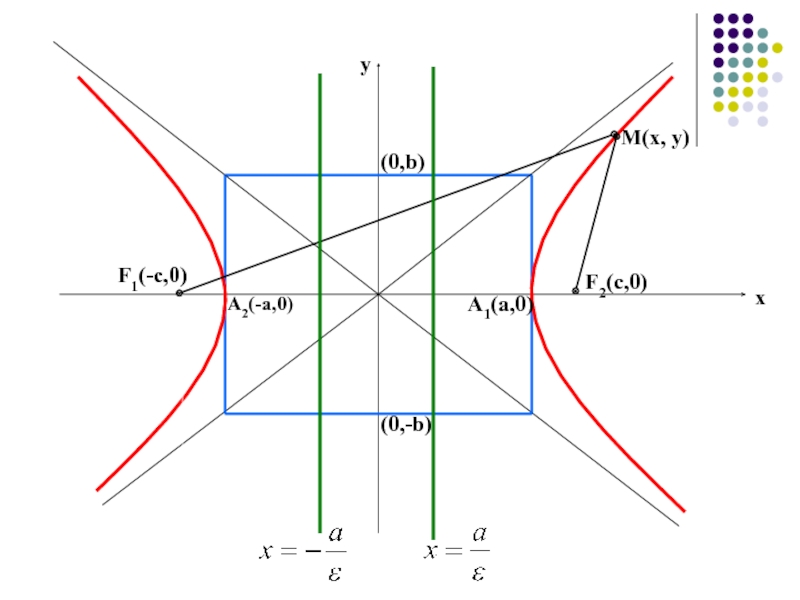
каждой из которых до двух данных точек этой плоскости ,

называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

F1, F2 – фокусы гиперболы, причем расстояние между ними обозначим 2с,
М – произвольная точка гиперболы.
По определению имеем: 2a<2c, т.е. a

оси Ох, а начало координат совпадало с серединой отрезка F1F2

. Тогда координаты фокусов F1(-c,0) и F2(c,0). Точка М имеет координаты (х,у).
По определению имеем:

причем 2а<2c, т.е. аВыведем уравнение гиперболы.

симметричен относительно точки О(0,0) – центра гиперболы.
Гипербола пересекает ось Ох

в точках А1(а,0) и A2(-а,0); с осью Оу гипербола общих точек не имеет.
Все точки гиперболы лежат справа от прямой х=а (правая ветвь) и слева от прямой х=-а (левая ветвь).
Гипербола имеет вершины, действительную и мнимую оси.
Прямые являются асимптотами гиперболы.

полуоси а, т.е.

причем

т.к. c>a.
С учетом того, что с2-а2=b2 получаем:

директрисами гиперболы.
Теорема.
Если r – расстояние от произвольной точки гиперболы

до какого-нибудь фокуса, d – расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение есть постоянная величина, равная эксцентриситету гиперболы, т.е.

А2(-а,0)
(0,-b)