Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности
Содержание
- 1. Поверхности
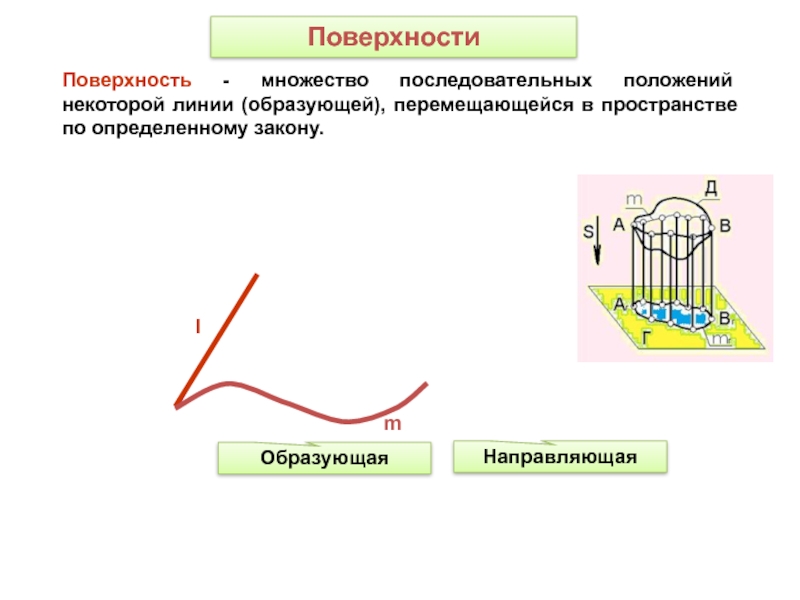
- 2. lОбразующаяНаправляющаяmПоверхность - множество последовательных положений некоторой линии (образующей), перемещающейся в пространстве по определенному закону.Поверхности
- 3. Линия, которая при перемещении образует поверхность, называется
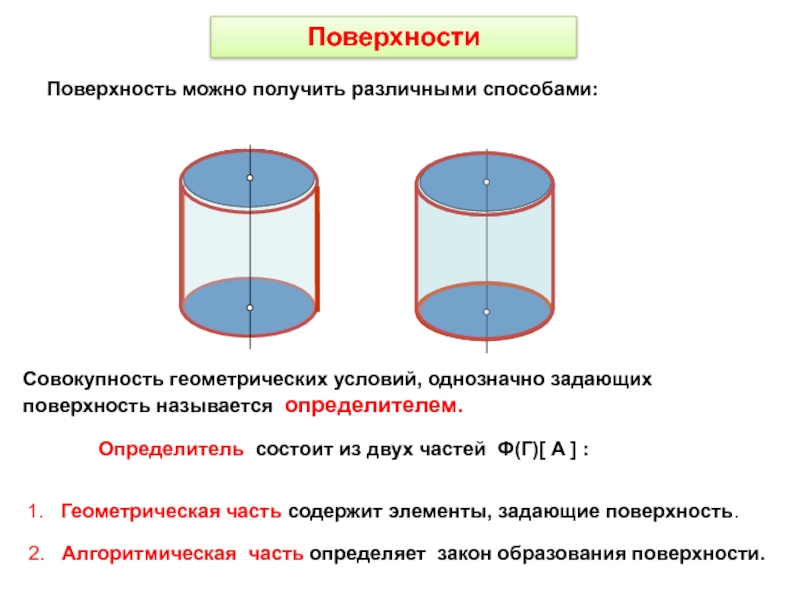
- 4. ПоверхностиПоверхность можно получить различными способами:Совокупность геометрических условий,
- 5. Классификация поверхностей
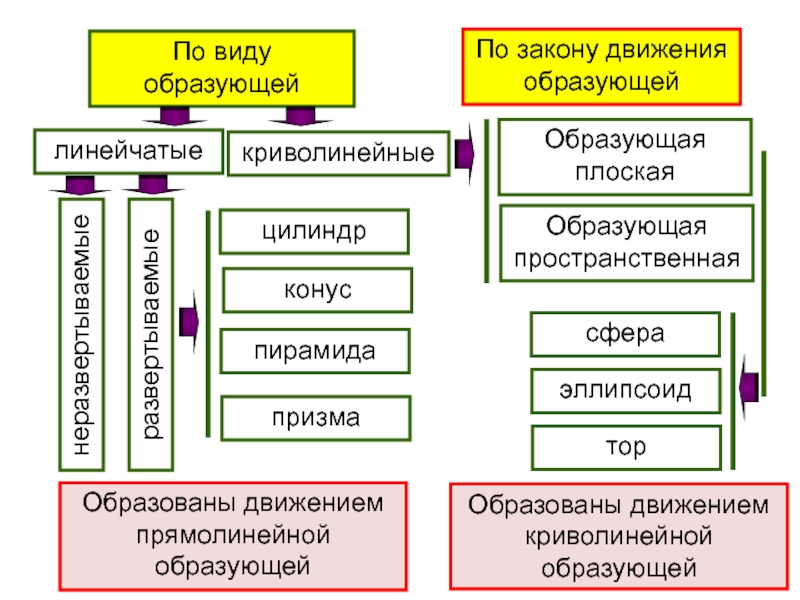
- 6. По виду образующейПо закону движения образующейлинейчатыекриволинейныеразвертываемыенеразвертываемыецилиндрконуспирамидапризмаОбразующая плоскаяОбразующая пространственнаясфераэллипсоидторОбразованы движением прямолинейной образующейОбразованы движением криволинейной образующей
- 7. КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ По виду образующей различают
- 8. ЗНАЧИТЕЛЬНЫЙ КЛАСС ПОВЕРХНОСТЕЙ ФОРМИРУЕТСЯ ДВИЖЕНИЕМ ОКРУЖНОСТИ ПОСТОЯННОГО ИЛИ ПЕРЕМЕННОГО РАДИУСА. ЭТО ТАК НАЗЫВАЕМЫЕ ЦИКЛИЧЕСКИЕ ПОВЕРХНОСТИЦиклическая поверхность
- 9. ЕСЛИ ЖЕ ГРУППИРОВАТЬ ПОВЕРХНОСТИ ПО ЗАКОНУ ДВИЖЕНИЯ
- 10. ПОВЕРХНОСТИ ВРАЩЕНИЯ ПОВЕРХНОСТИ ВРАЩЕНИЯ –
- 11. ТАК СОЗДАЕТСЯ КАРКАС ПОВЕРХНОСТИ, СОСТОЯЩЕЙ ИЗ
- 12. СФЕРА – ОБРАЗУЕТСЯ ВРАЩЕНИЕМ ОКРУЖНОСТИ
- 13. ТОР – ОБРАЗУЕТСЯ ПРИ ВРАЩЕНИИ ОКРУЖНОСТИ ВОКРУГ
- 14. ПАРАБОЛОИД ВРАЩЕНИЯ – ОБРАЗУЕТСЯ ПРИ ВРАЩЕНИИ ПАРАБОЛЫ ВОКРУГ СВОЕЙ ОСИ Параболоид вращения
- 15. ГИПЕРБОЛОИД ВРАЩЕНИЯ – РАЗЛИЧАЮТ ОДНО И
- 16. ВИНТОВЫЕ ПОВЕРХНОСТИВинтовые поверхности образуются винтовым движением некоторой
- 17. АЛГОРИТМИЧЕСКАЯ ЧАСТЬ: 1. НА ОБРАЗУЮЩЕЙ M ВЫДЕЛЯЮТ
- 18. ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА (ПОВЕРХНОСТИ КАТАЛАНА)Поверхность
- 19. В ЗАВИСИМОСТИ ОТ ФОРМЫ НАПРАВЛЯЮЩИХ ОБРАЗУЮТСЯ ТРИ
- 20. КОНОИД. КОНОИДОМ НАЗЫВАЕТСЯ ПОВЕРХНОСТЬ, ОБРАЗОВАННАЯ
- 21. ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД. ГИПЕРБОЛИЧЕСКИМ ПАРАБОЛОИДОМ ИЛИ
- 22. Поверхности параллельного переносаПоверхностью параллельного переноса называется поверхность,
- 23. Цилиндрическая поверхностьℓm∆(m; ℓ ⎜⎜S)S////Цилиндрическая поверхность образуется движением
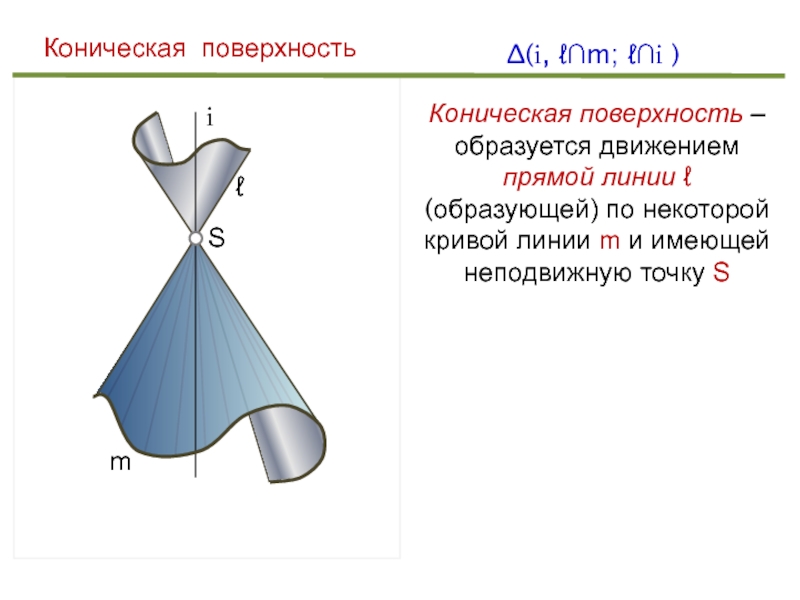
- 24. imℓ∆(i, ℓ∩m; ℓ∩i )Коническая поверхностьКоническая поверхность –
- 25. Однополостный гиперболоид
- 26. Вогнутый тор (глобоид)Поверхность, образованная внутренней стороной вращающейся дуги радиусом R, называется глобоидом
- 27. RRА2 ≡(В2 ) А1АВ1
- 28. A2(A1)Сфера
- 29. Выпуклый торRRА2А1RВ1С2≡(D2)(C1) ≡(D1) ≡≡(В2)i2
- 30. Эллипсоид
- 31. Открытый тор (окружность m вращается вокруг оси i )i2i1i3m3
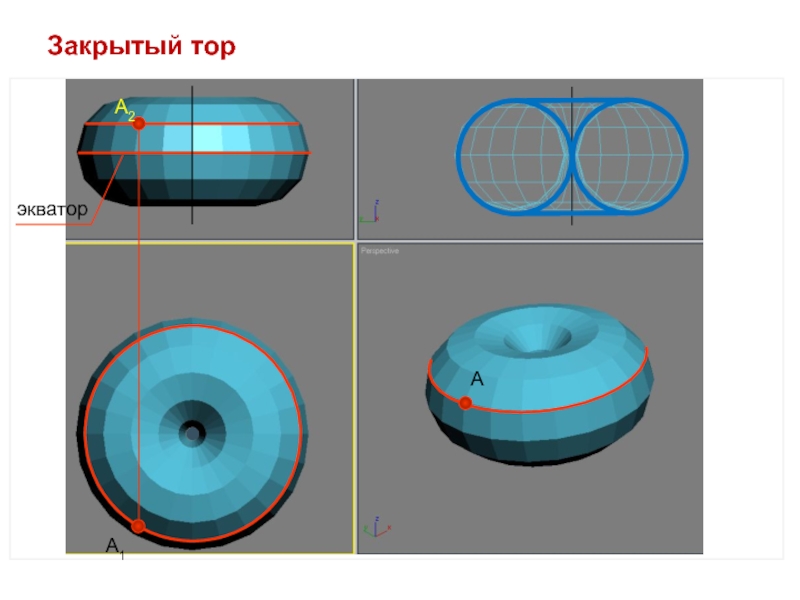
- 32. Закрытый торА2А1Аэкватор
- 33. Закрытый кольцевой тор (самопересекающийся)
- 34. Слайд 34
- 35. Слайд 35
- 36. Гранные поверхностиПирамидальная поверхность – это линейчатая поверхность,
- 37. M1А112N1S1Гранные поверхностиМногогранником называют замкнутые пространственные фигуры, ограниченные
- 38. Многогранные поверхности – это поверхности, образованные частями
- 39. Построение проекций многогранника сводится к построению проекций его вершин и ребер.
- 40. SℓmSmПирамидальная поверхностьSmПирамидаm – замкнутый контурЕсли направляющая m
- 41. m SℓПризматическая поверхностьm SℓПризмаЕсли все образующие поверхности
- 42. Примеры многогранных поверхностей
- 43. ПРАВИЛЬНЫЙ ШЕСТИГРАННИК (КУБ) ИЛИ ГЕКСАЭДР - ЧАСТНЫЙ
- 44. ПРАВИЛЬНЫЙ ВОСЬМИГРАННИК ИЛИ ОКТАЭДР - МНОГОГРАННИК, СОСТОЯЩИЙ
- 45. ПРАВИЛЬНЫЙ ДВАДЦАТИГРАННИК ИЛИ ИКОСАЭДР СОСТОИТ ИЗ ДВАДЦАТИ
- 46. Призматоид
- 47. Следует запомнить:Проекции точек , принадлежащих поверхности геометрического
- 48. Построение точки на поверхности многогранника: в плоскости
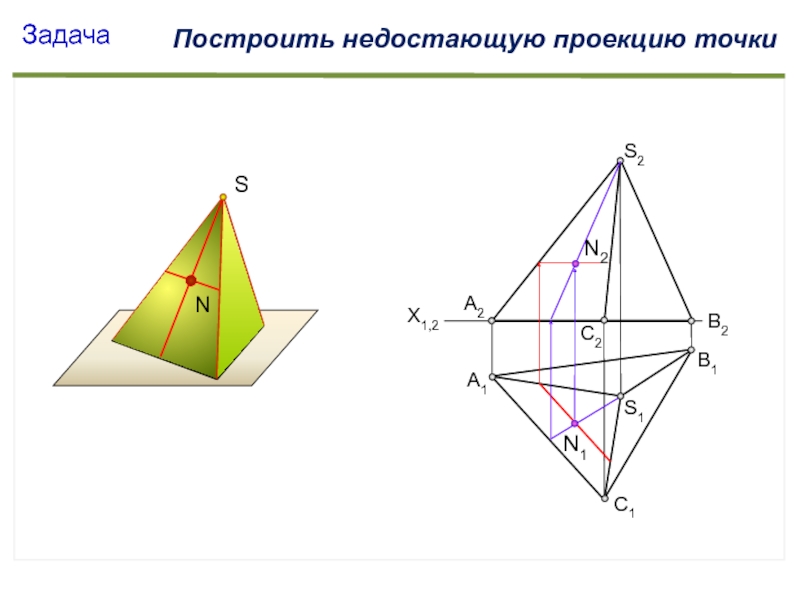
- 49. SА1С1В1S2X1,2S1А2С2В2ЗадачаПостроить недостающую проекцию точкиNN2N1
- 50. Поверхности вращения
- 51. ПоверхностиПоверхность задана на чертеже, если заданы проекции
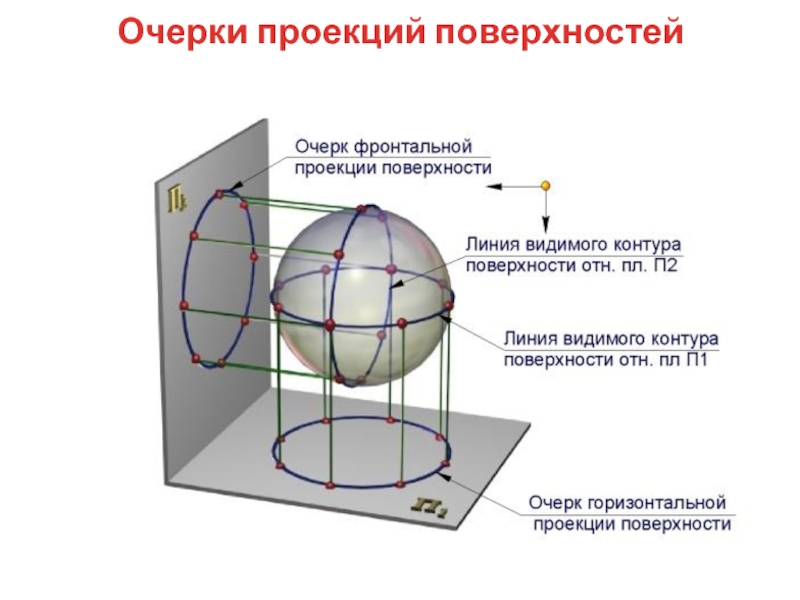
- 52. Очерки проекций поверхностей
- 53. Линии, образующие внешний контур
- 54. 1211Цилиндрическая поверхность –поверхность, образованная вращением прямолинейной образующей
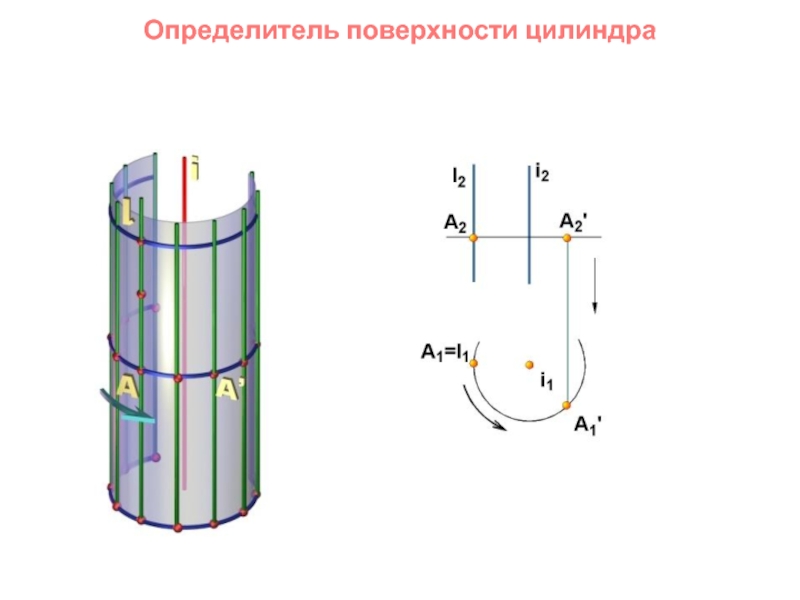
- 55. Определитель поверхности цилиндра
- 56. Определитель проверхности конуса
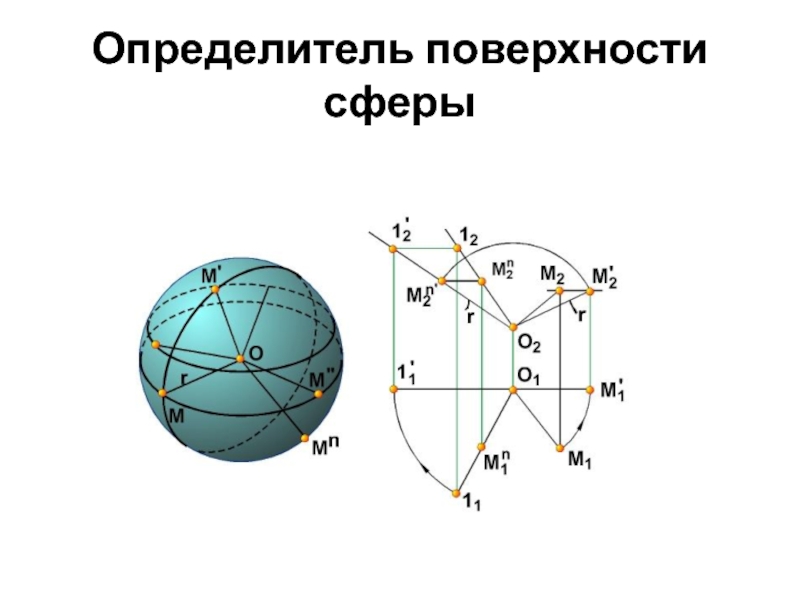
- 57. Определитель поверхности сферы
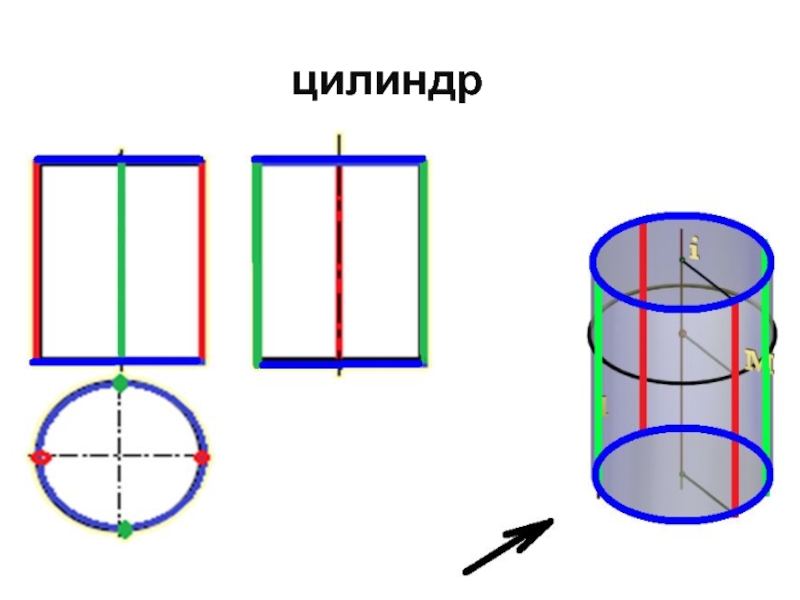
- 58. цилиндр
- 59. цилиндр131112
- 60. Слайд 60
- 61. Слайд 61
- 62. Точка принадлежит поверхности, если она принадлежит линии,
- 63. Линейчатые поверхности вращенияКоническая поверхность –поверхность, образованная
- 64. 31Образующаяось32Σ ( l, i) [ l ∩ i] – коническая поверхностьЛинейчатые поверхности вращения
- 65. 41Образующаяось42Σ ( l, i) [ l ∩ i] – коническая поверхностьЛинейчатые поверхности вращения
- 66. Слайд 66
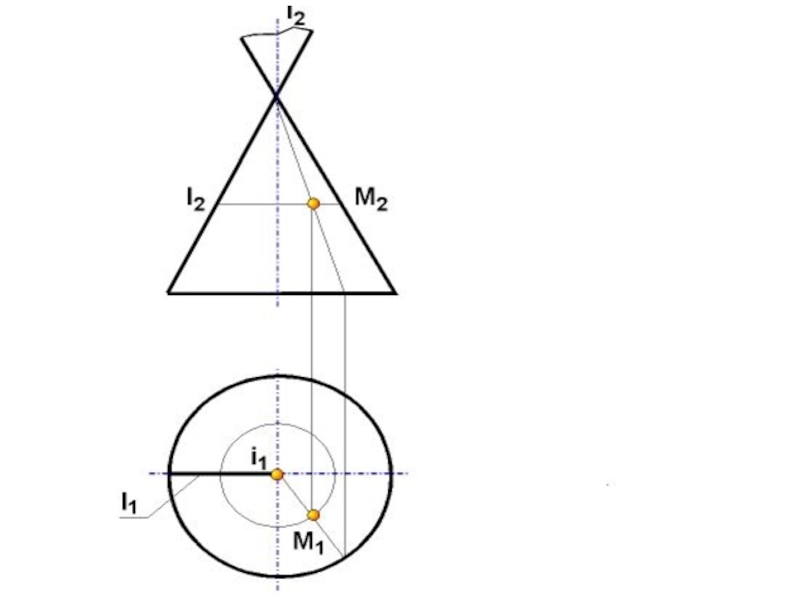
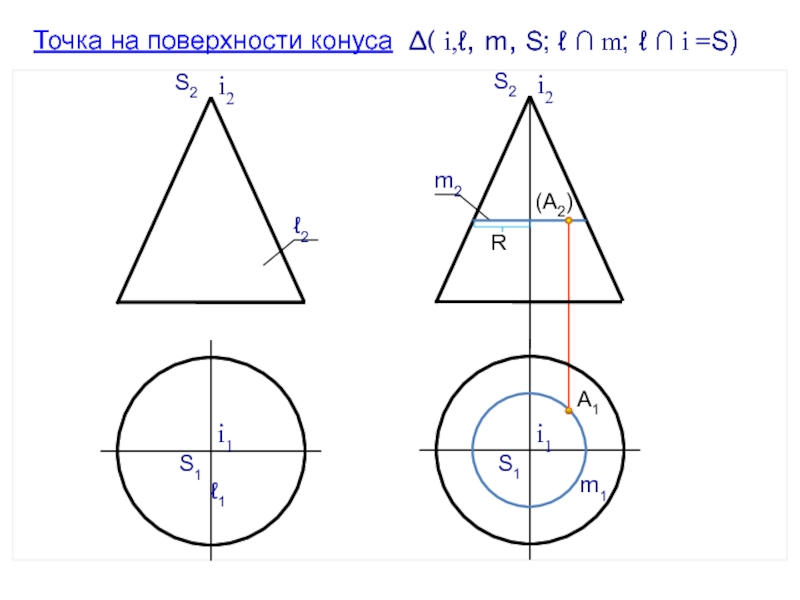
- 67. А2А1i2S2∆( i,ℓ, m, S; ℓ ∩ m; ℓ ∩ i =S)ℓ2S1i1ℓ1(А2)А1i2S2m2S1i1m1Точка на поверхности конусаR
- 68. СФЕРА
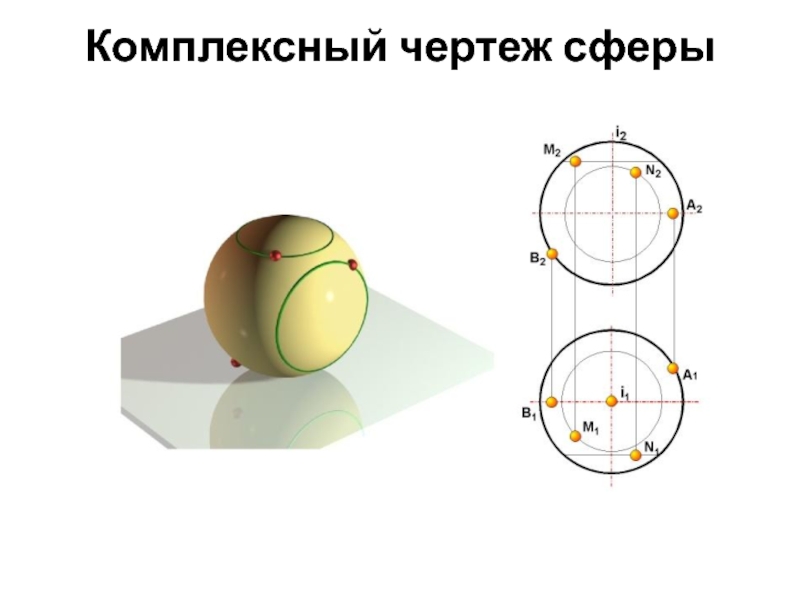
- 69. Комплексный чертеж сферы
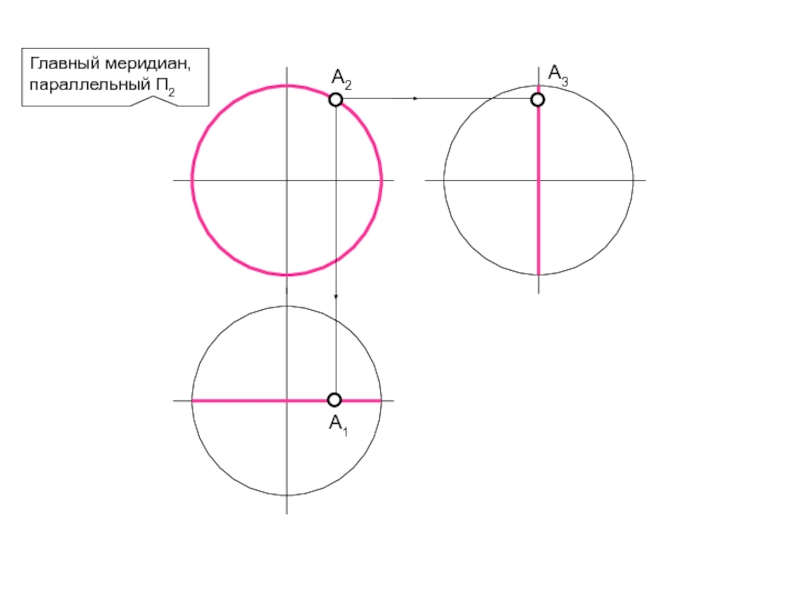
- 70. Главный меридиан, параллельный П2А2А1А3
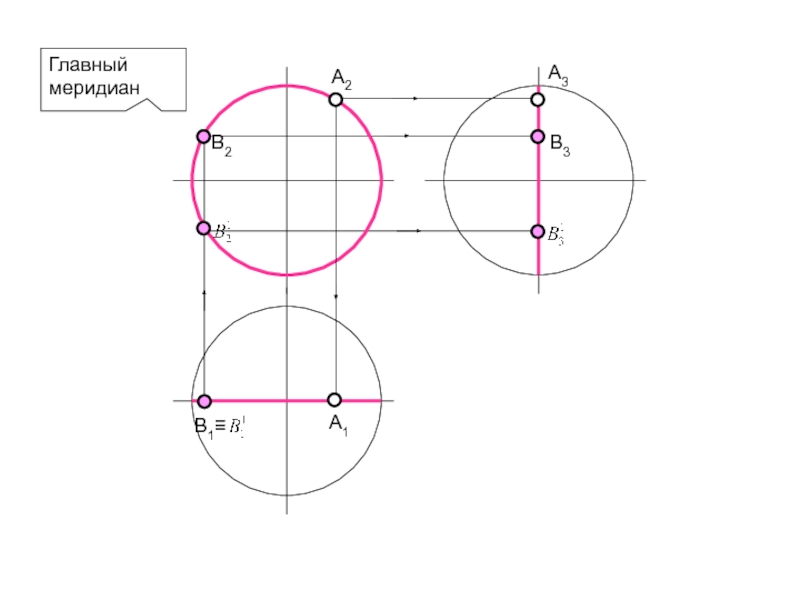
- 71. Главный меридианВ2В3
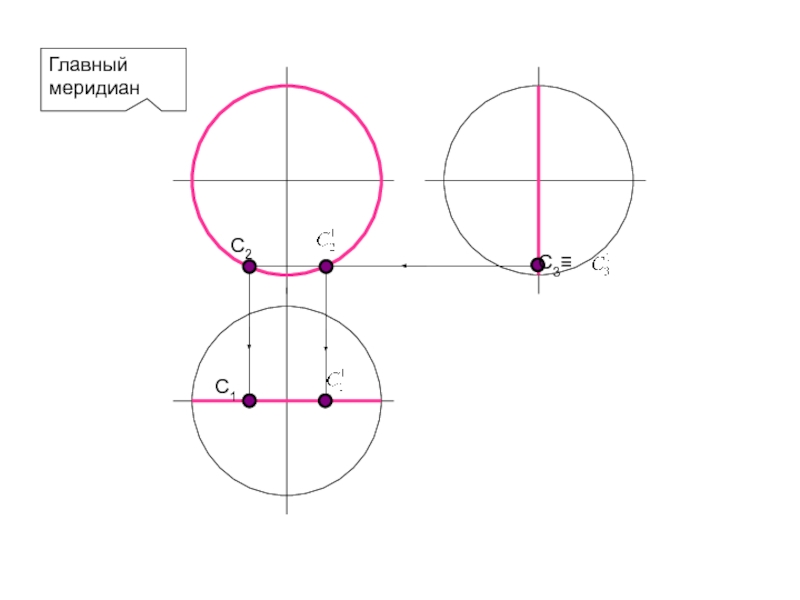
- 72. Главный меридианC1C2
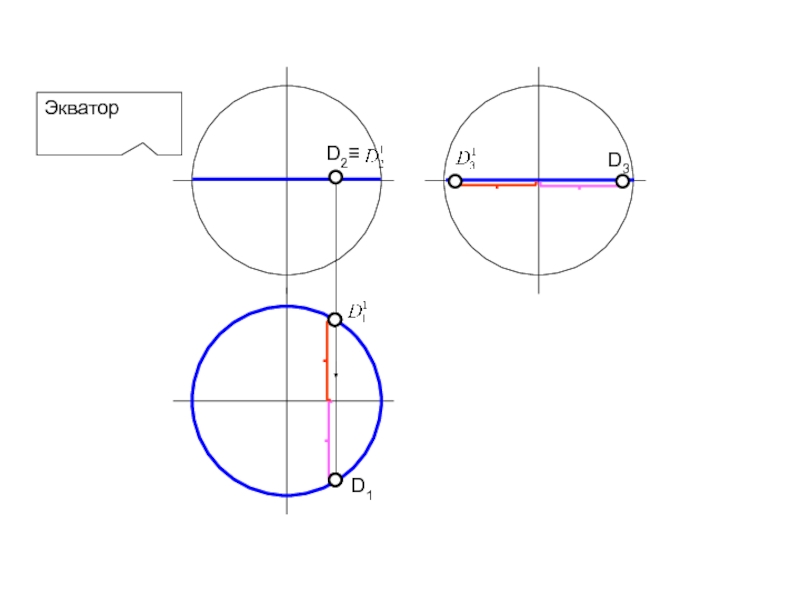
- 73. ЭкваторD1D3
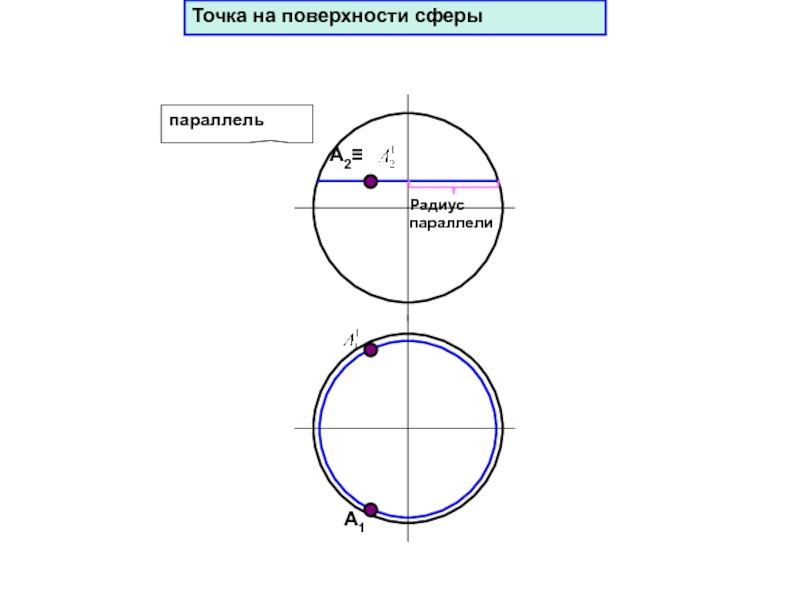
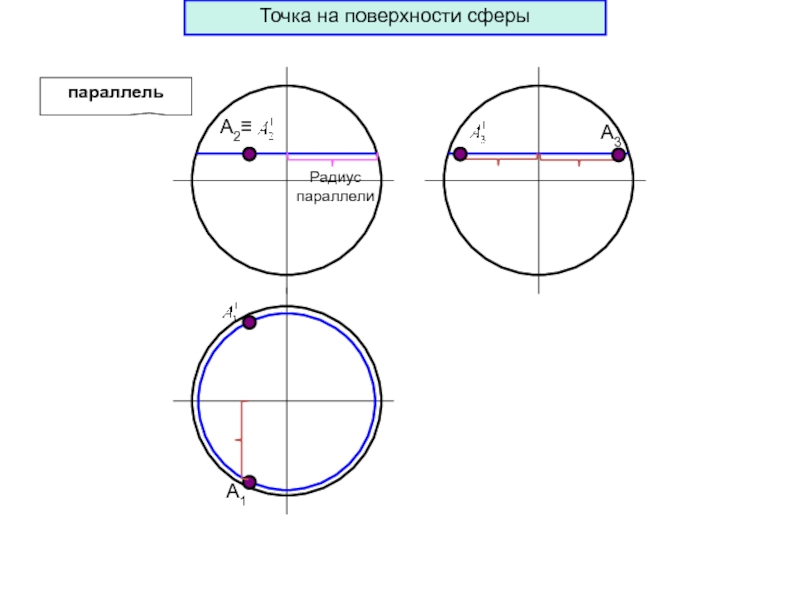
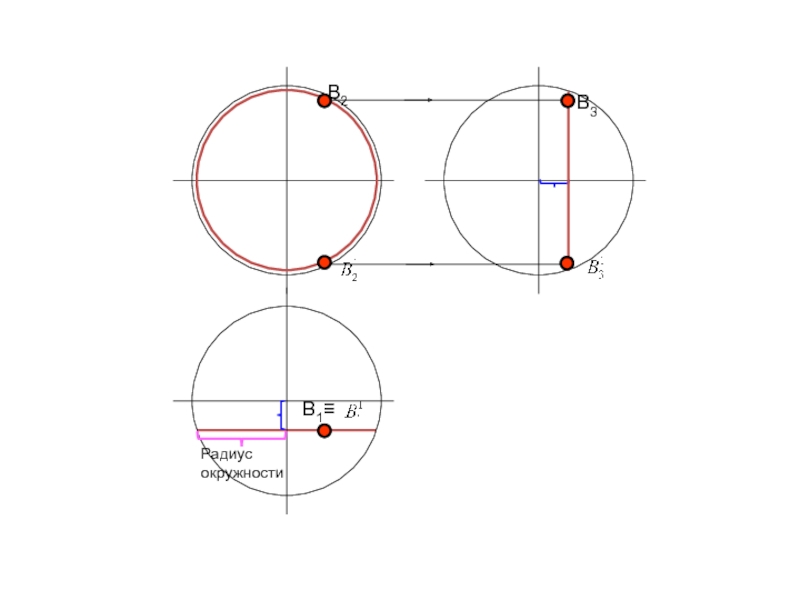
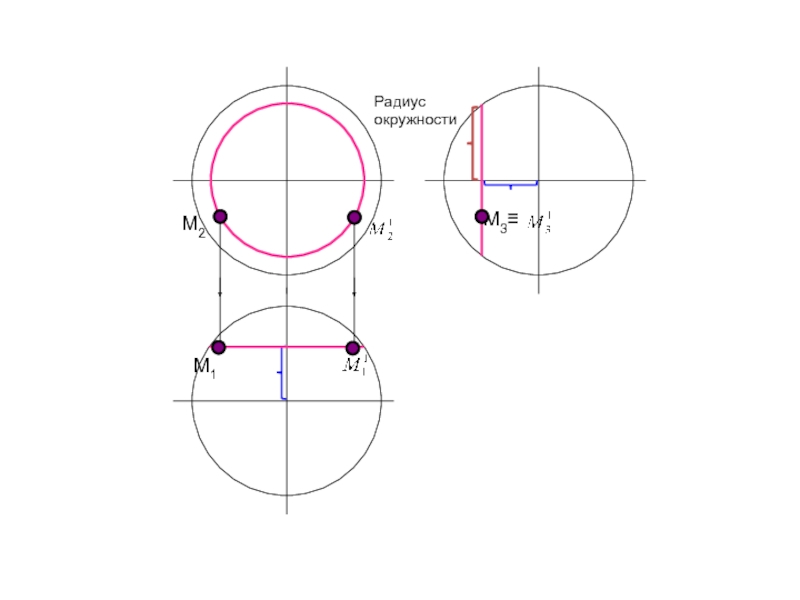
- 74. А1параллельРадиус параллелиТочка на поверхности сферы
- 75. А1параллельА3Радиус параллелиТочка на поверхности сферы
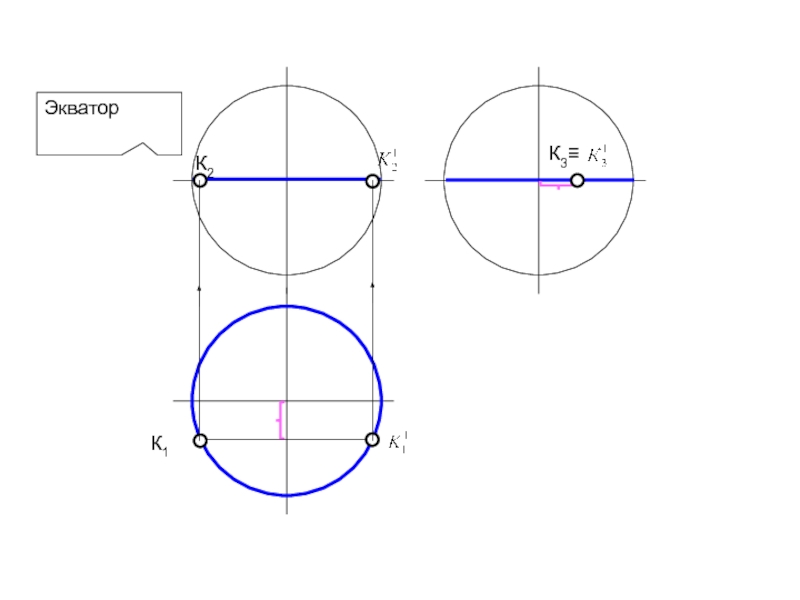
- 76. ЭкваторК1
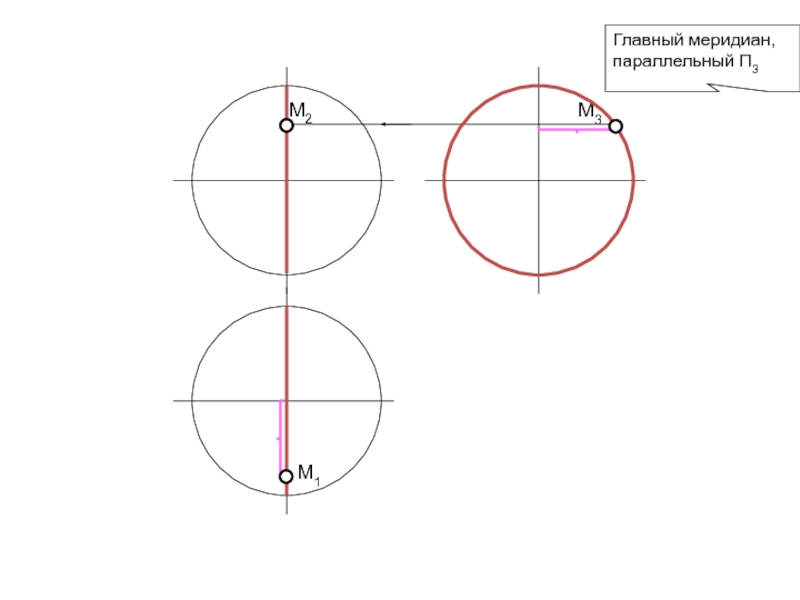
- 77. Главный меридиан, параллельный П3М3М2М1
- 78. Радиус окружности
- 79. Радиус окружности
- 80. Обычно геометрические тела изображаются в их простейших
- 81. ***Построение комплексных чертежей начинают с тех плоскостей проекций, на которые их основания проецируются в натуральную величину.
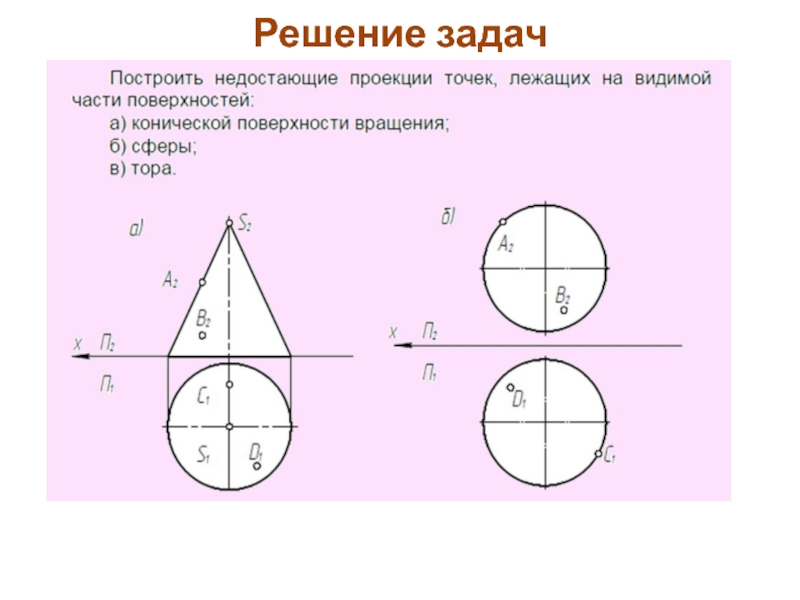
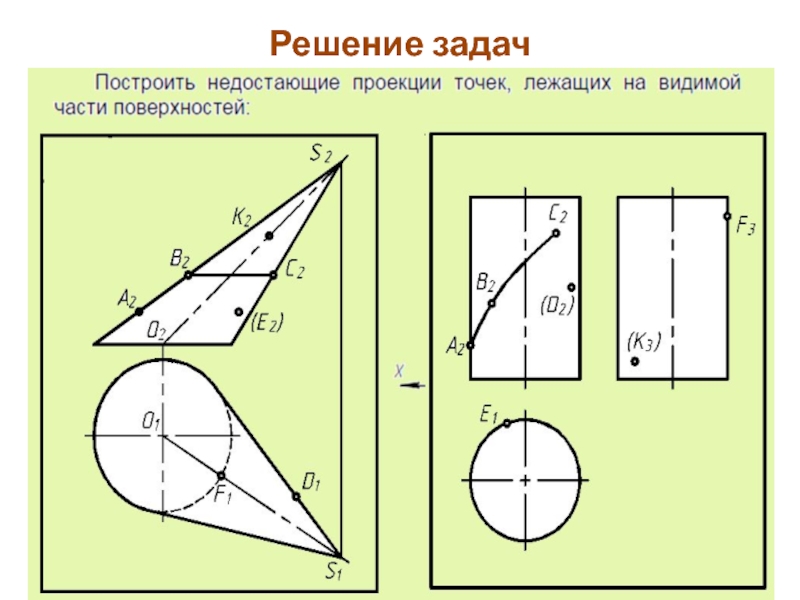
- 82. Решение задач
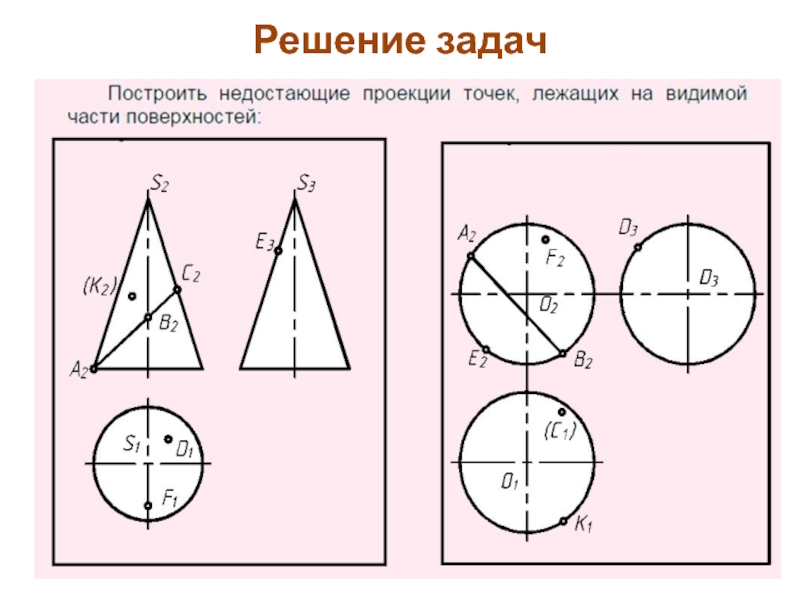
- 83. Решение задач
- 84. Решение задач
- 85. Среди точек кривой выделяют опорные точки:– экстремальные
- 86. Скачать презентанцию
lОбразующаяНаправляющаяmПоверхность - множество последовательных положений некоторой линии (образующей), перемещающейся в пространстве по определенному закону.Поверхности
Слайды и текст этой презентации
Слайд 2l
Образующая
Направляющая
m
Поверхность - множество последовательных положений некоторой линии (образующей), перемещающейся в
пространстве по определенному закону.
Слайд 3Линия, которая при перемещении образует поверхность, называется образующей.
Линии, которые остаются
неподвижными и с которыми при своем движении пересекается образующая, называются
направляющими.
Слайд 4
Поверхности
Поверхность можно получить различными способами:
Совокупность геометрических условий, однозначно задающих поверхность
называется определителем.
Определитель состоит из двух частей Ф(Г)[ A ] :
1.
Геометрическая часть содержит элементы, задающие поверхность.2. Алгоритмическая часть определяет закон образования поверхности.
Слайд 6По виду образующей
По закону движения образующей
линейчатые
криволинейные
развертываемые
неразвертываемые
цилиндр
конус
пирамида
призма
Образующая плоская
Образующая пространственная
сфера
эллипсоид
тор
Образованы движением прямолинейной
образующей
Образованы движением криволинейной образующей
Слайд 7КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ
По виду образующей различают поверхности линейчатые и нелинейчатые.
Линейчатые поверхности
- поверхности, которые могут быть образованы с помощью прямой линии.
Нелинейчатые поверхности - поверхности, которые могут быть образованы только с помощью кривой линии.Линейчатые поверхности в свою очередь разделяют на так называемые развертывающие и неразвертывающиеся.
Развертывающиеся поверхности - поверхности, которые после разреза их по образующей могут быть совмещены с плоскостью без наличия разрывов и складок. Неразвертывающиеся поверхности - поверхности, которые не могут быть совмещены с плоскостью без наличия разрывов и складок. Нелинейчатые поверхности разделяются на поверхности с постоянной образующей и поверхности с переменной образующей. Поверхности с постоянной образующей - поверхности, образующая которых не изменяет своей формы в процессе образования поверхности. Поверхности с переменной образующей - поверхности, образующая которых изменяется в процессе образования поверхности.
Слайд 8ЗНАЧИТЕЛЬНЫЙ КЛАСС ПОВЕРХНОСТЕЙ ФОРМИРУЕТСЯ ДВИЖЕНИЕМ ОКРУЖНОСТИ ПОСТОЯННОГО ИЛИ ПЕРЕМЕННОГО РАДИУСА.
ЭТО ТАК НАЗЫВАЕМЫЕ ЦИКЛИЧЕСКИЕ ПОВЕРХНОСТИ
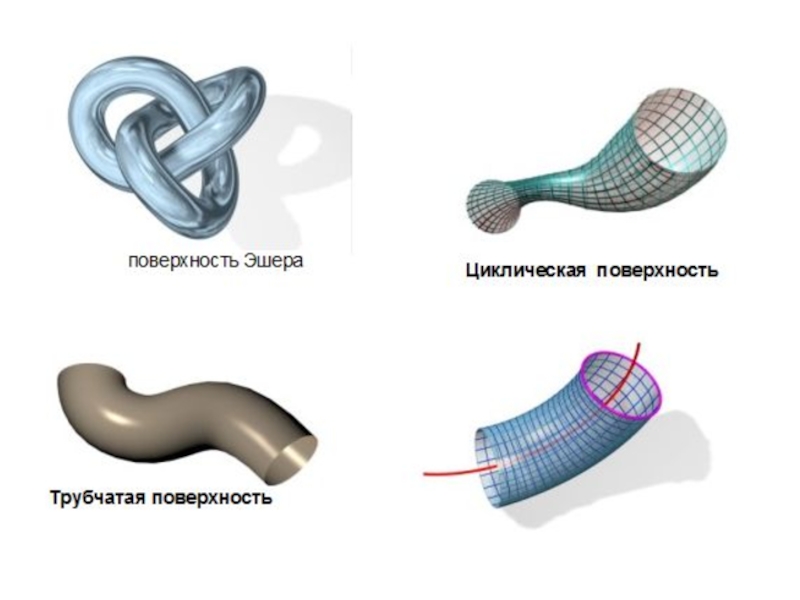
Циклическая поверхность
Слайд 9ЕСЛИ ЖЕ ГРУППИРОВАТЬ ПОВЕРХНОСТИ ПО ЗАКОНУ ДВИЖЕНИЯ ОБРАЗУЮЩЕЙ ЛИНИИ И
ПРОИЗВОДЯЩЕЙ ПОВЕРХНОСТИ, ТО БОЛЬШИНСТВО ВСТРЕЧАЮЩИХСЯ В ТЕХНИКЕ ПОВЕРХНОСТЕЙ МОЖНО РАЗДЕЛИТЬ
НА:· поверхности вращения;
· винтовые поверхности;
· поверхности с плоскостью параллелизма;
· поверхности параллельного переноса.
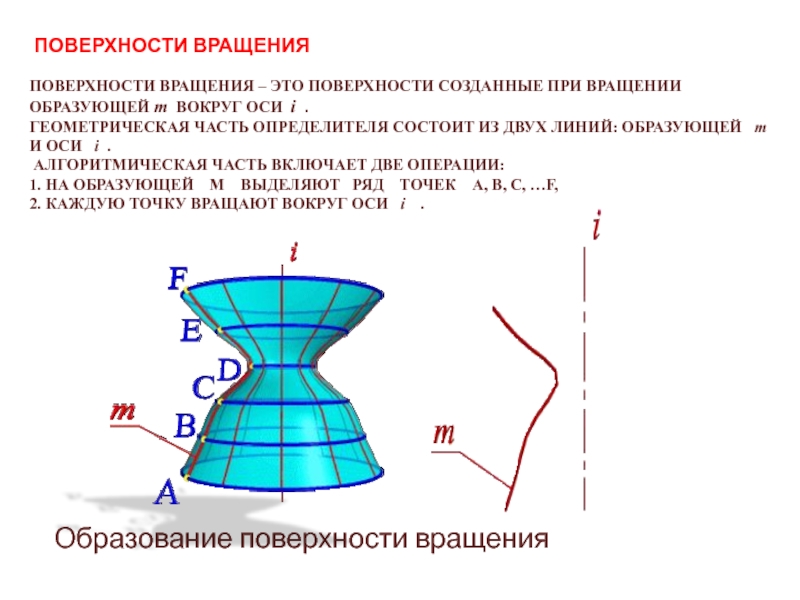
Слайд 10 ПОВЕРХНОСТИ ВРАЩЕНИЯ ПОВЕРХНОСТИ ВРАЩЕНИЯ – ЭТО ПОВЕРХНОСТИ СОЗДАННЫЕ ПРИ ВРАЩЕНИИ
ОБРАЗУЮЩЕЙ m ВОКРУГ ОСИ i . ГЕОМЕТРИЧЕСКАЯ ЧАСТЬ ОПРЕДЕЛИТЕЛЯ СОСТОИТ ИЗ
ДВУХ ЛИНИЙ: ОБРАЗУЮЩЕЙ m И ОСИ i . АЛГОРИТМИЧЕСКАЯ ЧАСТЬ ВКЛЮЧАЕТ ДВЕ ОПЕРАЦИИ: 1. НА ОБРАЗУЮЩЕЙ M ВЫДЕЛЯЮТ РЯД ТОЧЕК A, B, C, …F, 2. КАЖДУЮ ТОЧКУ ВРАЩАЮТ ВОКРУГ ОСИ i .Образование поверхности вращения
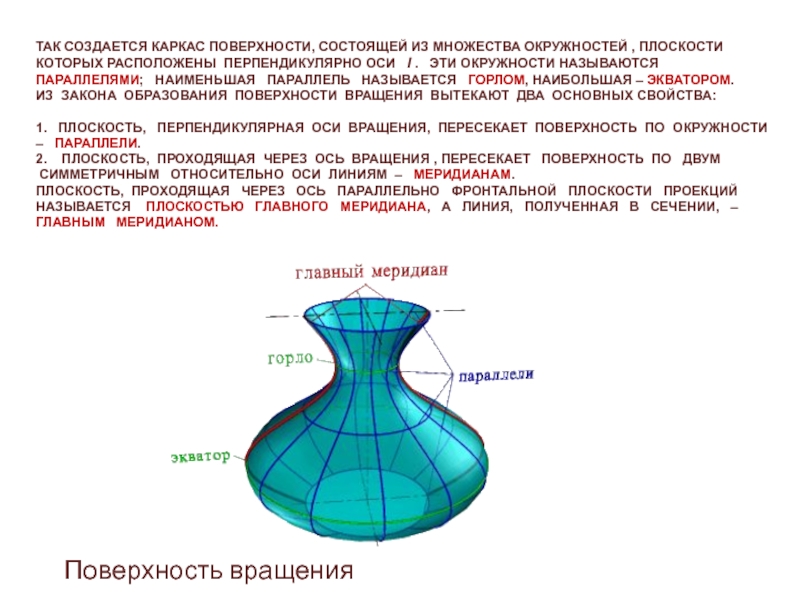
Слайд 11 ТАК СОЗДАЕТСЯ КАРКАС ПОВЕРХНОСТИ, СОСТОЯЩЕЙ ИЗ МНОЖЕСТВА ОКРУЖНОСТЕЙ , ПЛОСКОСТИ
КОТОРЫХ РАСПОЛОЖЕНЫ ПЕРПЕНДИКУЛЯРНО ОСИ I . ЭТИ ОКРУЖНОСТИ
НАЗЫВАЮТСЯ ПАРАЛЛЕЛЯМИ; НАИМЕНЬШАЯ ПАРАЛЛЕЛЬ НАЗЫВАЕТСЯ ГОРЛОМ, НАИБОЛЬШАЯ – ЭКВАТОРОМ. ИЗ ЗАКОНА ОБРАЗОВАНИЯ ПОВЕРХНОСТИ ВРАЩЕНИЯ ВЫТЕКАЮТ ДВА ОСНОВНЫХ СВОЙСТВА: 1. ПЛОСКОСТЬ, ПЕРПЕНДИКУЛЯРНАЯ ОСИ ВРАЩЕНИЯ, ПЕРЕСЕКАЕТ ПОВЕРХНОСТЬ ПО ОКРУЖНОСТИ – ПАРАЛЛЕЛИ. 2. ПЛОСКОСТЬ, ПРОХОДЯЩАЯ ЧЕРЕЗ ОСЬ ВРАЩЕНИЯ , ПЕРЕСЕКАЕТ ПОВЕРХНОСТЬ ПО ДВУМ СИММЕТРИЧНЫМ ОТНОСИТЕЛЬНО ОСИ ЛИНИЯМ – МЕРИДИАНАМ. ПЛОСКОСТЬ, ПРОХОДЯЩАЯ ЧЕРЕЗ ОСЬ ПАРАЛЛЕЛЬНО ФРОНТАЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ НАЗЫВАЕТСЯ ПЛОСКОСТЬЮ ГЛАВНОГО МЕРИДИАНА, А ЛИНИЯ, ПОЛУЧЕННАЯ В СЕЧЕНИИ, – ГЛАВНЫМ МЕРИДИАНОМ.Поверхность вращения
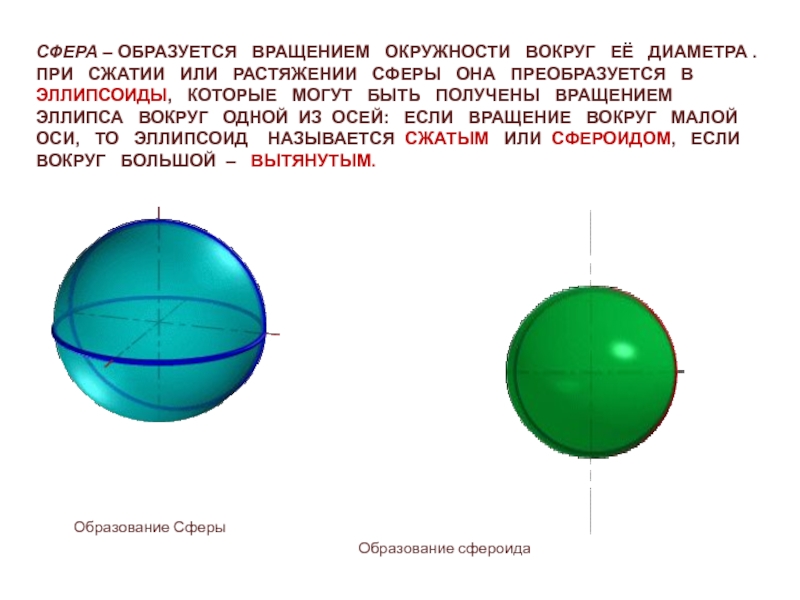
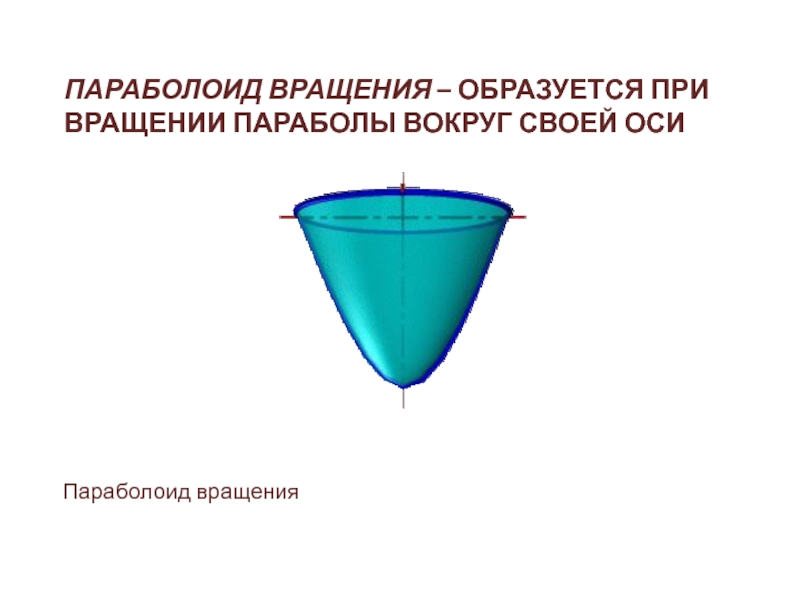
Слайд 12СФЕРА – ОБРАЗУЕТСЯ ВРАЩЕНИЕМ ОКРУЖНОСТИ ВОКРУГ
ЕЁ ДИАМЕТРА . ПРИ СЖАТИИ ИЛИ РАСТЯЖЕНИИ
СФЕРЫ ОНА ПРЕОБРАЗУЕТСЯ В ЭЛЛИПСОИДЫ, КОТОРЫЕ МОГУТ БЫТЬ ПОЛУЧЕНЫ ВРАЩЕНИЕМ ЭЛЛИПСА ВОКРУГ ОДНОЙ ИЗ ОСЕЙ: ЕСЛИ ВРАЩЕНИЕ ВОКРУГ МАЛОЙ ОСИ, ТО ЭЛЛИПСОИД НАЗЫВАЕТСЯ СЖАТЫМ ИЛИ СФЕРОИДОМ, ЕСЛИ ВОКРУГ БОЛЬШОЙ – ВЫТЯНУТЫМ. Образование Сферы
Образование сфероида
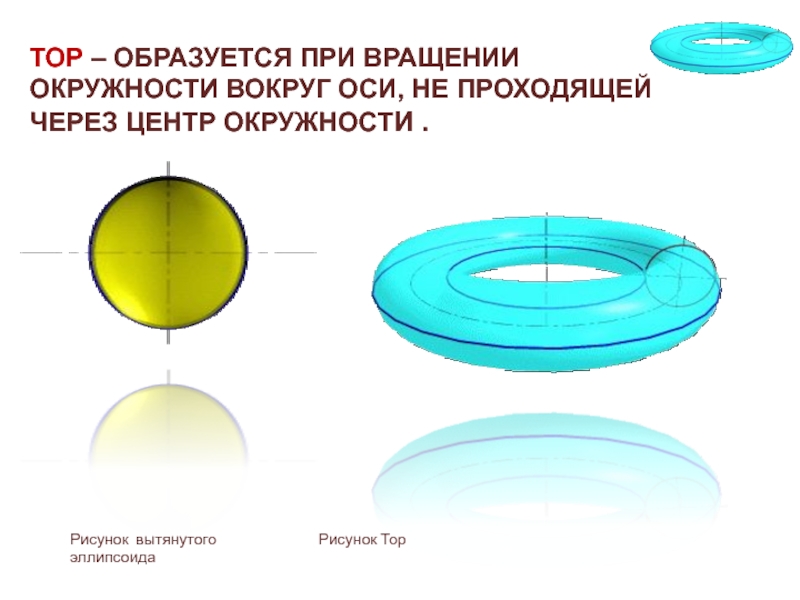
Слайд 13ТОР – ОБРАЗУЕТСЯ ПРИ ВРАЩЕНИИ ОКРУЖНОСТИ ВОКРУГ ОСИ, НЕ ПРОХОДЯЩЕЙ
ЧЕРЕЗ ЦЕНТР ОКРУЖНОСТИ .
Рисунок вытянутого
Рисунок Торэллипсоида
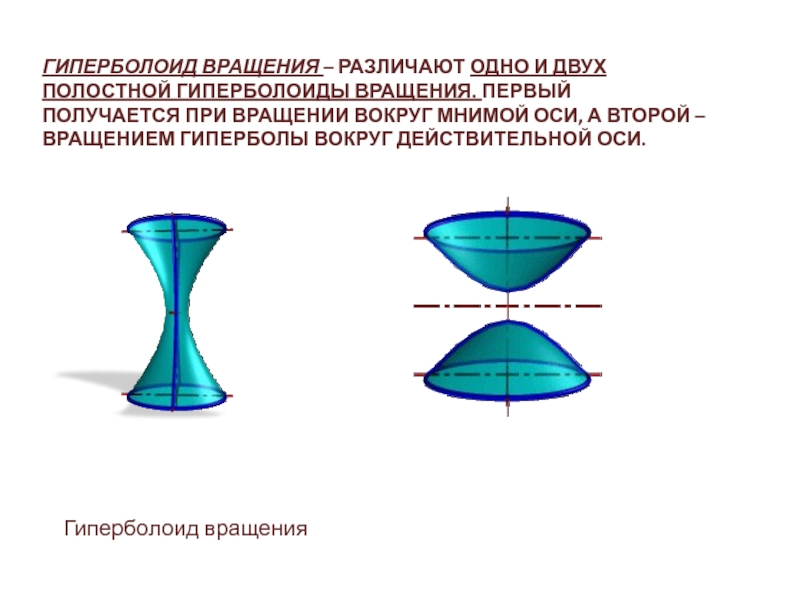
Слайд 15 ГИПЕРБОЛОИД ВРАЩЕНИЯ – РАЗЛИЧАЮТ ОДНО И ДВУХ ПОЛОСТНОЙ ГИПЕРБОЛОИДЫ ВРАЩЕНИЯ.
ПЕРВЫЙ ПОЛУЧАЕТСЯ ПРИ ВРАЩЕНИИ ВОКРУГ МНИМОЙ ОСИ, А ВТОРОЙ –
ВРАЩЕНИЕМ ГИПЕРБОЛЫ ВОКРУГ ДЕЙСТВИТЕЛЬНОЙ ОСИ.Гиперболоид вращения
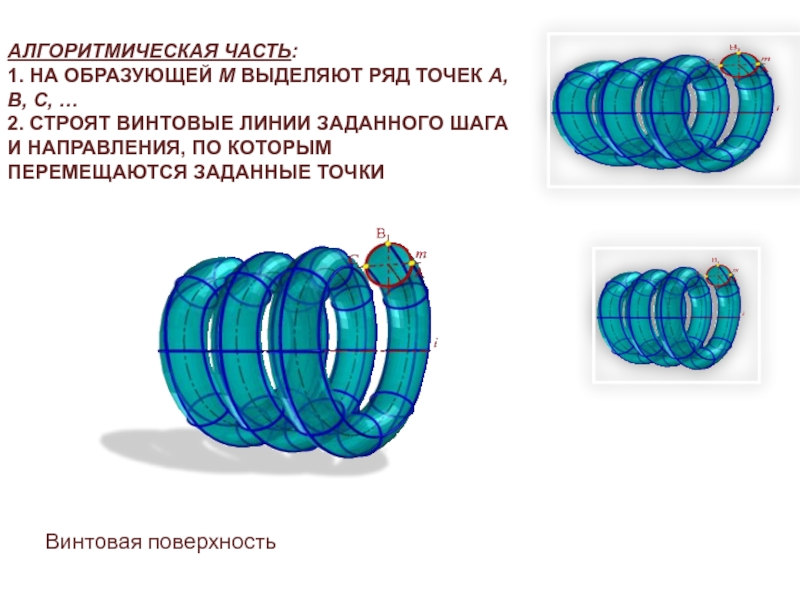
Слайд 16ВИНТОВЫЕ ПОВЕРХНОСТИ
Винтовые поверхности образуются винтовым движением некоторой линии – образующей.
Под
винтовым движением понимается совокупность двух движений: поступательного параллельно некоторой оси,
и вращательного, вокруг той же оси.Геометрическая часть определителя винтовой поверхности ничем не отличается от поверхности вращения и состоит из двух линий: образующей m и оси i .
Слайд 17АЛГОРИТМИЧЕСКАЯ ЧАСТЬ: 1. НА ОБРАЗУЮЩЕЙ M ВЫДЕЛЯЮТ РЯД ТОЧЕК А, В,
С, … 2. СТРОЯТ ВИНТОВЫЕ ЛИНИИ ЗАДАННОГО ШАГА И НАПРАВЛЕНИЯ, ПО
КОТОРЫМ ПЕРЕМЕЩАЮТСЯ ЗАДАННЫЕ ТОЧКИВинтовая поверхность
Слайд 18ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА
(ПОВЕРХНОСТИ КАТАЛАНА)
Поверхность с плоскостью параллелизма представляет
собой множество прямых линий l (образующих), параллельных некоторой плоскости α
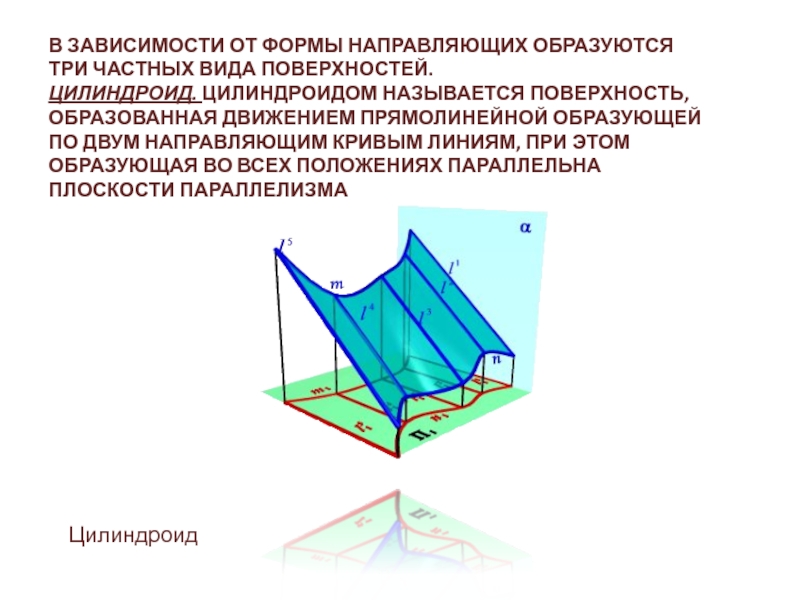
(плоскости параллелизма) и пересекающих две данные направляющие m, n
Слайд 19В ЗАВИСИМОСТИ ОТ ФОРМЫ НАПРАВЛЯЮЩИХ ОБРАЗУЮТСЯ ТРИ ЧАСТНЫХ ВИДА ПОВЕРХНОСТЕЙ. ЦИЛИНДРОИД.
ЦИЛИНДРОИДОМ НАЗЫВАЕТСЯ ПОВЕРХНОСТЬ, ОБРАЗОВАННАЯ ДВИЖЕНИЕМ ПРЯМОЛИНЕЙНОЙ ОБРАЗУЮЩЕЙ ПО ДВУМ НАПРАВЛЯЮЩИМ
КРИВЫМ ЛИНИЯМ, ПРИ ЭТОМ ОБРАЗУЮЩАЯ ВО ВСЕХ ПОЛОЖЕНИЯХ ПАРАЛЛЕЛЬНА ПЛОСКОСТИ ПАРАЛЛЕЛИЗМА Цилиндроид
Слайд 20КОНОИД. КОНОИДОМ НАЗЫВАЕТСЯ ПОВЕРХНОСТЬ, ОБРАЗОВАННАЯ ДВИЖЕНИЕМ
ПРЯМОЛИНЕЙНОЙ ОБРАЗУЮЩЕЙ ПО ДВУМ НАПРАВЛЯЮЩИМ, ОДНА
ИЗ КОТОРЫХ КРИВАЯ ЛИНИЯ, А ДРУГАЯ ПРЯМАЯ, ПРИ ЭТОМ ОБРАЗУЮЩАЯ ВО ВСЕХ ПОЛОЖЕНИЯХ ПАРАЛЛЕЛЬНА ПЛОСКОСТИ ПАРАЛЛЕЛИЗМА Коноид
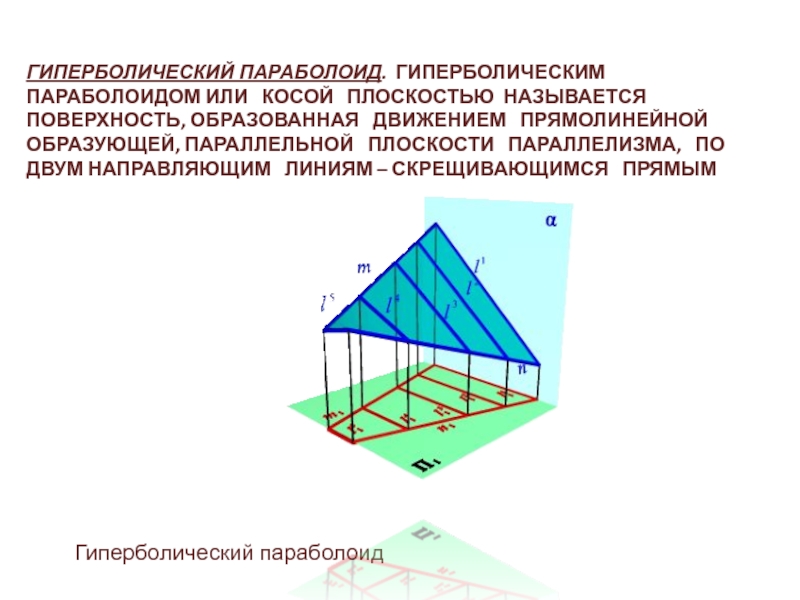
Слайд 21ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД. ГИПЕРБОЛИЧЕСКИМ ПАРАБОЛОИДОМ ИЛИ КОСОЙ ПЛОСКОСТЬЮ
НАЗЫВАЕТСЯ ПОВЕРХНОСТЬ, ОБРАЗОВАННАЯ ДВИЖЕНИЕМ ПРЯМОЛИНЕЙНОЙ ОБРАЗУЮЩЕЙ,
ПАРАЛЛЕЛЬНОЙ ПЛОСКОСТИ ПАРАЛЛЕЛИЗМА, ПО ДВУМ НАПРАВЛЯЮЩИМ ЛИНИЯМ – СКРЕЩИВАЮЩИМСЯ ПРЯМЫМ Гиперболический параболоид
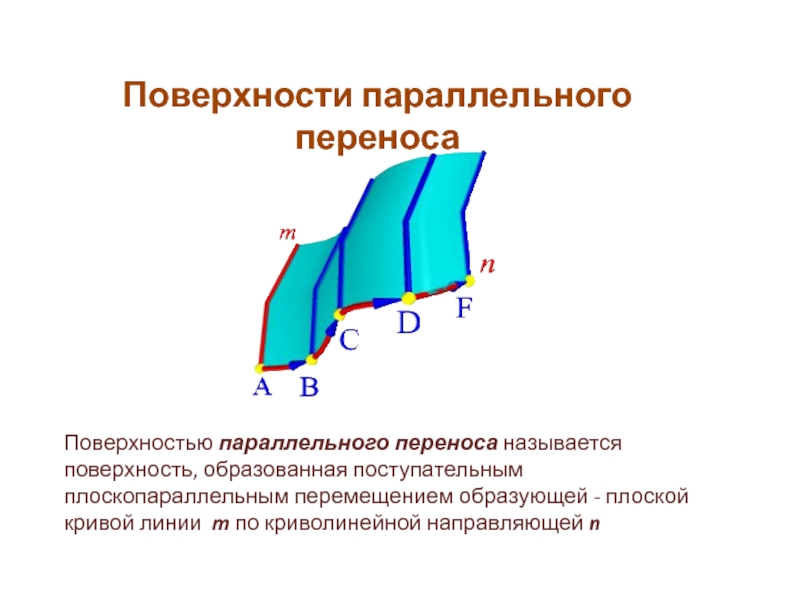
Слайд 22Поверхности параллельного переноса
Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным
перемещением образующей - плоской кривой линии m по криволинейной направляющей
n
Слайд 23
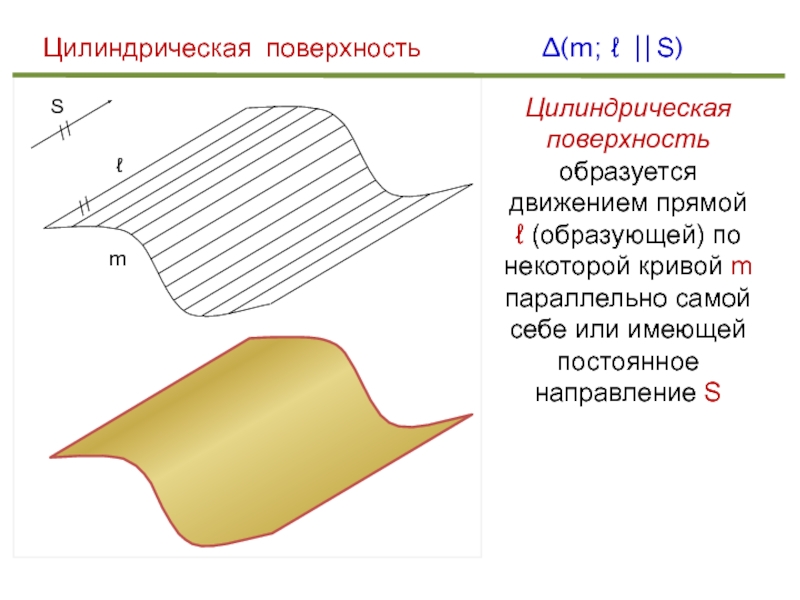
Цилиндрическая поверхность
ℓ
m
∆(m; ℓ ⎜⎜S)
S
//
//
Цилиндрическая поверхность образуется движением прямой ℓ (образующей)
по некоторой кривой m параллельно самой себе или имеющей постоянное
направление S
Слайд 24
i
m
ℓ
∆(i, ℓ∩m; ℓ∩i )
Коническая поверхность
Коническая поверхность – образуется движением прямой
линии ℓ (образующей) по некоторой кривой линии m и имеющей
неподвижную точку SS
Слайд 26Вогнутый тор (глобоид)
Поверхность, образованная внутренней стороной вращающейся дуги радиусом R,
называется глобоидом
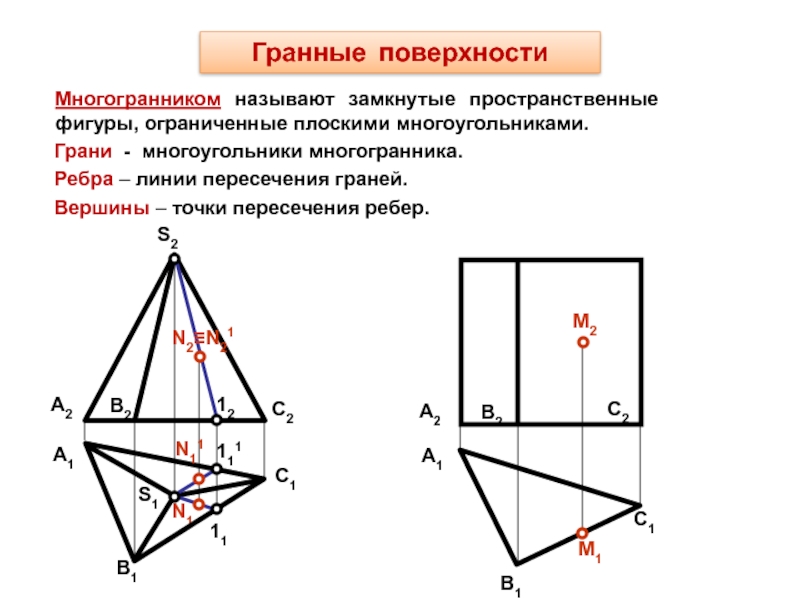
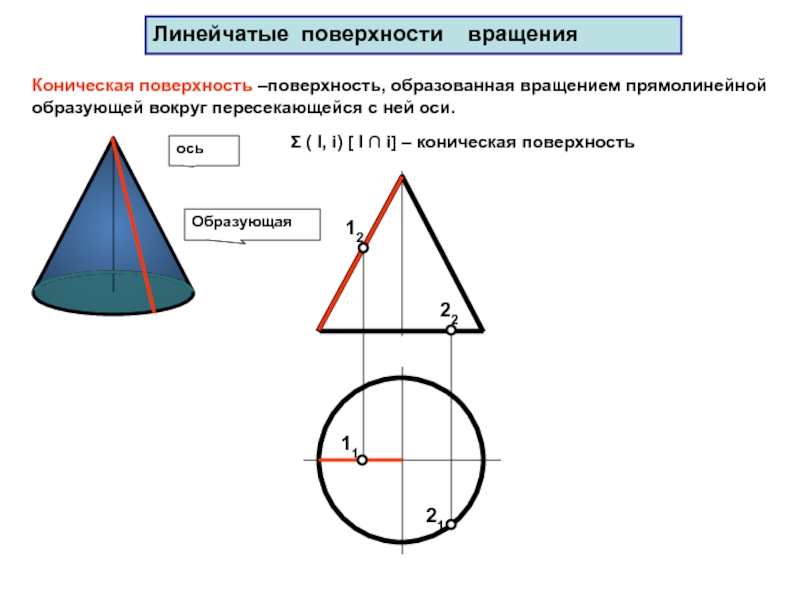
Слайд 36Гранные поверхности
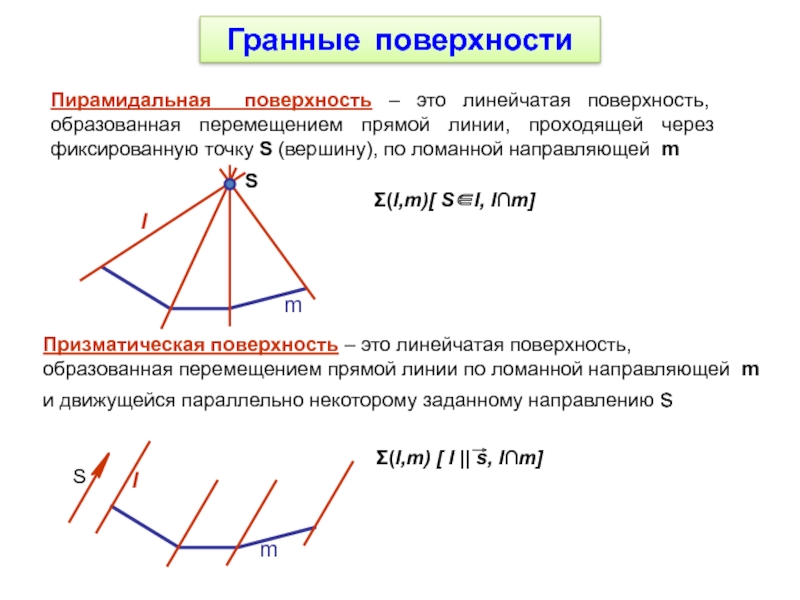
Пирамидальная поверхность – это линейчатая поверхность, образованная перемещением прямой
линии, проходящей через фиксированную точку S (вершину), по ломанной направляющей
mS
Призматическая поверхность – это линейчатая поверхность, образованная перемещением прямой линии по ломанной направляющей m и движущейся параллельно некоторому заданному направлению s
m
m
l
l
Σ(l,m)[ S∈l, l∩m]
Слайд 37M1
А1
12
N1
S1
Гранные поверхности
Многогранником называют замкнутые пространственные фигуры, ограниченные плоскими многоугольниками.
S2
N2≡N21
M2
Грани -
многоугольники многогранника.
Ребра – линии пересечения граней.
Вершины – точки пересечения ребер.
А2
В2
С2
С1
В1
А1
11
А2
В2
С2
С1
В1
111
N11
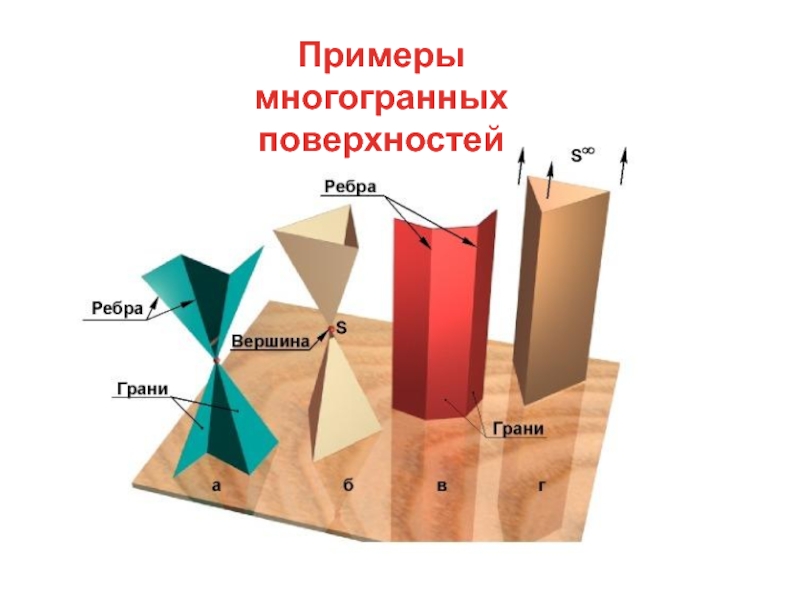
Слайд 38Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей
Многогранником
называется тело, ограниченное многогранной поверхностью, состоящей из плоских многоугольников
Отсеки
плоскостей называются гранями, а линии их пересечения – ребрами
Точки пересечения ребер называются вершинами
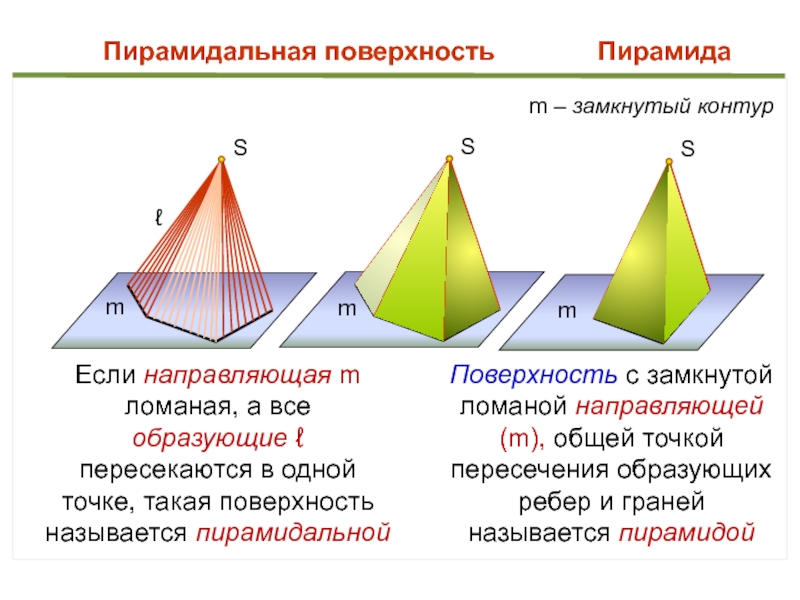
Слайд 40
S
ℓ
m
S
m
Пирамидальная поверхность
S
m
Пирамида
m – замкнутый контур
Если направляющая m ломаная, а все
образующие ℓ пересекаются в одной точке, такая поверхность называется пирамидальной
Поверхность с замкнутой ломаной направляющей (m), общей точкой пересечения образующих ребер и граней называется пирамидой
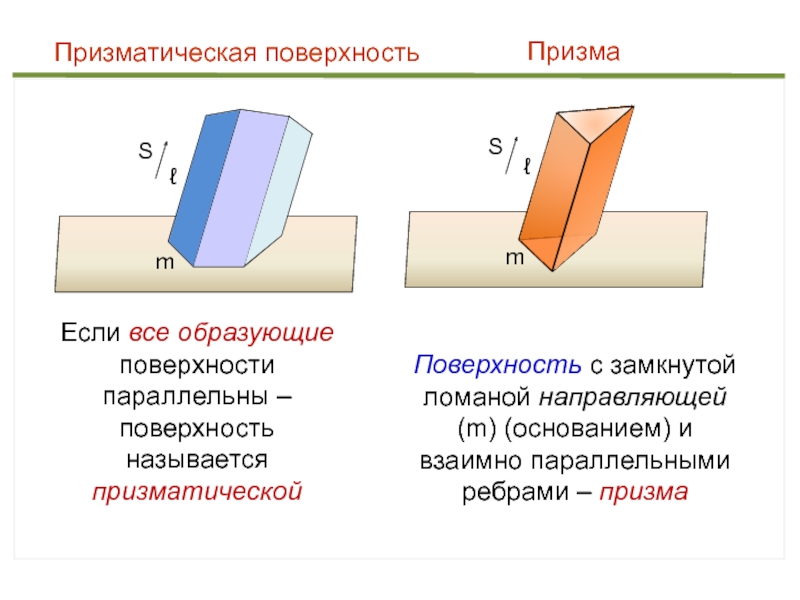
Слайд 41
m
S
ℓ
Призматическая поверхность
m
S
ℓ
Призма
Если все образующие поверхности параллельны – поверхность
называется призматической
Поверхность с замкнутой ломаной направляющей (m) (основанием) и взаимно
параллельными ребрами – призма 
Слайд 43ПРАВИЛЬНЫЙ ШЕСТИГРАННИК (КУБ) ИЛИ ГЕКСАЭДР - ЧАСТНЫЙ СЛУЧАЙ ПРЯМОЙ ПРИЗМЫ,
У КОТОРОЙ ОСНОВАНИЯ И БОКОВЫЕ ГРАНИ - КВАДРАТЫ.
Куб
Слайд 44ПРАВИЛЬНЫЙ ВОСЬМИГРАННИК ИЛИ ОКТАЭДР - МНОГОГРАННИК, СОСТОЯЩИЙ ИЗ ВОСЬМИ ГРАНЕЙ
- ПРАВИЛЬНЫХ ТРЕУГОЛЬНИКОВ, СОЕДИНЕННЫХ ПО ЧЕТЫРЕ В ОДНОЙ ВЕРШИНЕ. ОКТАЭДР
МОЖНО РАССМАТРИВАТЬ КАК ГЕОМЕТРИЧЕСКОЕ ТЕЛО, СОСТОЯЩЕЕ ИЗ ДВУХ ПИРАМИД С ОБЩИМ ОСНОВАНИЕМПравильный восьмигранник
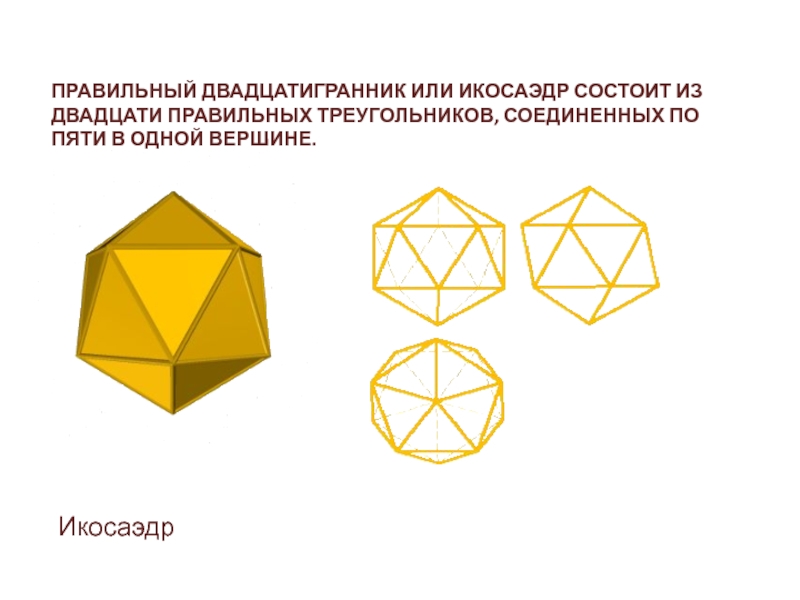
Слайд 45ПРАВИЛЬНЫЙ ДВАДЦАТИГРАННИК ИЛИ ИКОСАЭДР СОСТОИТ ИЗ ДВАДЦАТИ ПРАВИЛЬНЫХ ТРЕУГОЛЬНИКОВ, СОЕДИНЕННЫХ
ПО ПЯТИ В ОДНОЙ ВЕРШИНЕ.
Икосаэдр
Слайд 47Следует запомнить:
Проекции точек , принадлежащих поверхности геометрического тела, располагаются на
линиях очерка и внутри его, никакая точка поверхности тела не
может иметь свою проекцию за пределами очерка.
Слайд 48Построение точки на поверхности многогранника:
в плоскости грани проводят прямую
и на этой прямой находят точку.
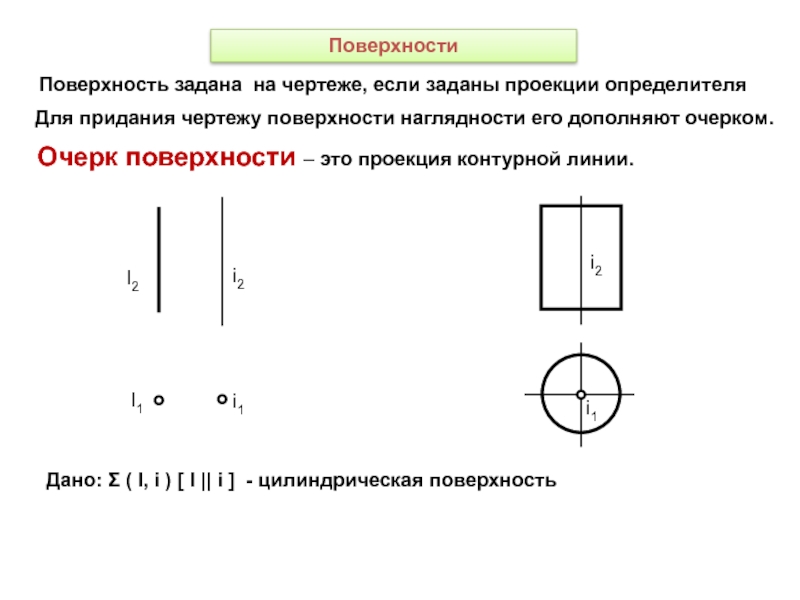
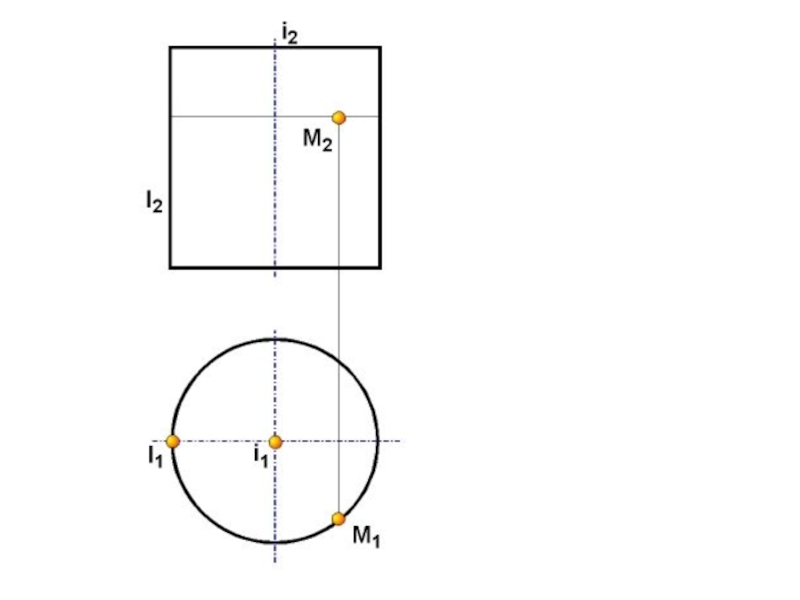
Слайд 51Поверхности
Поверхность задана на чертеже, если заданы проекции определителя
i2
i1
l2
l1
Для придания чертежу
поверхности наглядности его дополняют очерком.
Очерк поверхности – это проекция контурной
линии.Дано: Σ ( l, i ) [ l || i ] - цилиндрическая поверхность
i2
i1
Слайд 53 Линии, образующие внешний контур геометрического
тела, называют О Ч Е Р
К О М .Различают горизонтальный, фронтальный и профильный очерки.
ОЧЕРКИ проекций всегда видим. Видимость линий, расположенных внутри очерка определяется при помощи конкурирующих точек.
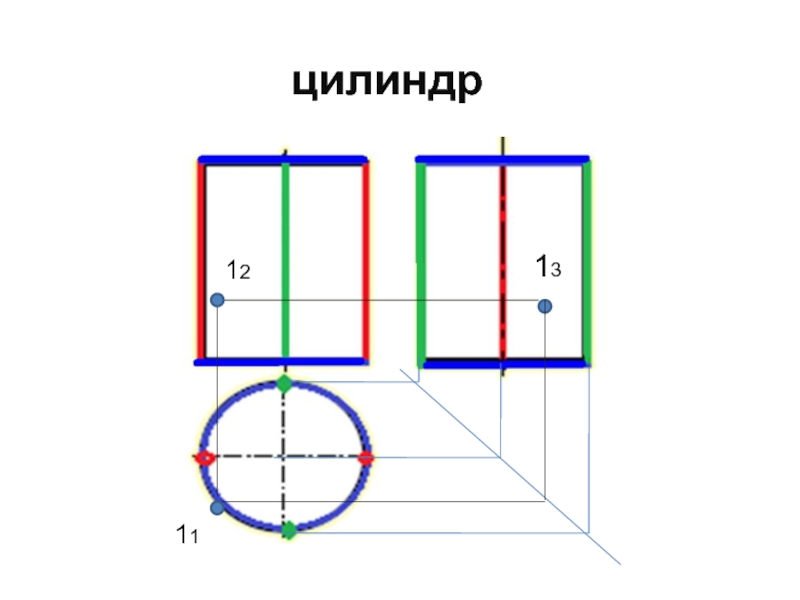
Слайд 5412
11
Цилиндрическая поверхность –поверхность, образованная вращением прямолинейной образующей вокруг оси.
Г (
l, i)[ l ||i ]– цилиндрическая поверхность
Образующая
ось
Линейчатые поверхности вращения
![1211Цилиндрическая поверхность –поверхность, образованная вращением прямолинейной образующей вокруг оси.Г ( l, i)[ l ||i ]– цилиндрическая поверхностьОбразующаяосьЛинейчатые](/img/thumbs/62ef41bacaf584ac3336a4c60845c0e0-800x.jpg "Поверхности 1211Цилиндрическая поверхность –поверхность, образованная вращением прямолинейной образующей вокруг оси.Г ( l,")
Слайд 62Точка принадлежит поверхности, если она принадлежит линии, расположенной на этой
поверхности
Линия принадлежит поверхности, если каждая ее точка принадлежит этой поверхности
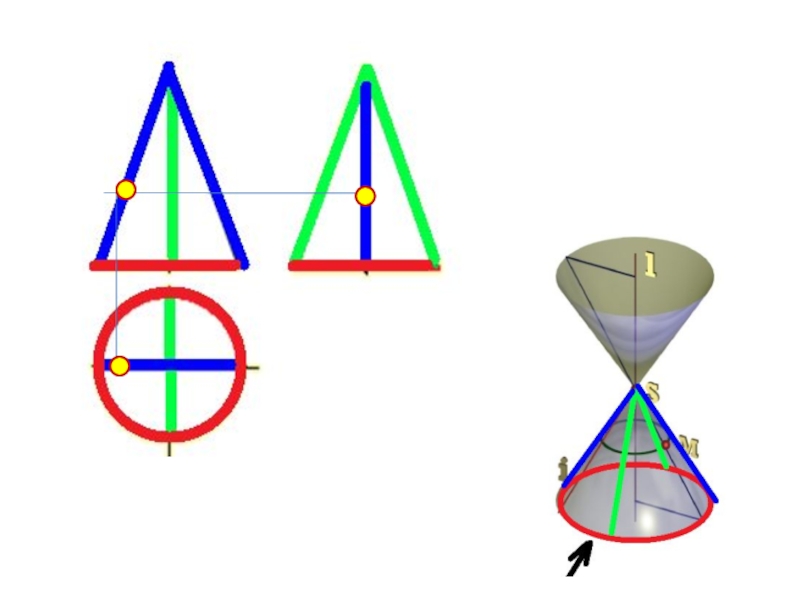
Слайд 63Линейчатые поверхности вращения
Коническая поверхность –поверхность, образованная вращением прямолинейной образующей
вокруг пересекающейся с ней оси.
Образующая
ось
Σ ( l, i) [ l
∩ i] – коническая поверхность12
11
22
21
![31Образующаяось32Σ ( l, i) [ l ∩ i] – коническая поверхностьЛинейчатые поверхности вращения](/img/thumbs/38bff0767c77db3c08466fdb4c253efb-800x.jpg "Поверхности 31Образующаяось32Σ ( l, i) [ l ∩ i] – коническая поверхностьЛинейчатые поверхности вращения")
![41Образующаяось42Σ ( l, i) [ l ∩ i] – коническая поверхностьЛинейчатые поверхности вращения](/img/thumbs/8ece80f7fe21f0c12de357eae9930c42-800x.jpg "Поверхности 41Образующаяось42Σ ( l, i) [ l ∩ i] – коническая поверхностьЛинейчатые поверхности вращения")
Слайд 67
А2
А1
i2
S2
∆( i,ℓ, m, S; ℓ ∩ m; ℓ ∩ i
=S)
ℓ2
S1
i1
ℓ1
(А2)
А1
i2
S2
m2
S1
i1
m1
Точка на поверхности конуса
R
Слайд 80
Обычно геометрические тела изображаются в их простейших положениях, наиболее выгодных
для проецирования, когда оси, образующие, ребра и грани проецируются на
одни плоскости проекций в натуральную величину, а на другие – в точки и линии.
Слайд 81***Построение комплексных чертежей начинают с тех плоскостей проекций, на которые
их основания проецируются в натуральную величину.
Слайд 85Среди точек кривой выделяют опорные точки:
– экстремальные точки – высшая
и низшая, крайняя левая и крайняя правая, самая далекая и
самая ближняя точки кривой;– граничные точки видимости кривой, принадлежащей поверхности, лежат на очерках поверхности и отделяют видимую часть поверхности от ее невидимой части
