Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реляционная алгебра
Содержание
- 1. Реляционная алгебра
- 2. Реляционная алгебраВведениеСтандартные операцииСвойства стандартных операцийСпециальные операции
- 3. Слайд 3
- 4. Теоретико-множественные операторы: Объединение Пересечение Вычитание Декартово произведение
- 5. Специальные реляционные операторы: Выборка Проекция Соединение Деление
- 6. Стандартные реляционные операцииОбъединение Объединением
- 7. Синтаксис операции объединения:A union BС = (A
- 8. Пример: Пусть даны два отношения
- 9. Пересечение
- 10. Синтаксис операции пересечения:A intersect BC = (A
- 11. Пример: Пусть даны два отношения
- 12. Вычитание Вычитанием
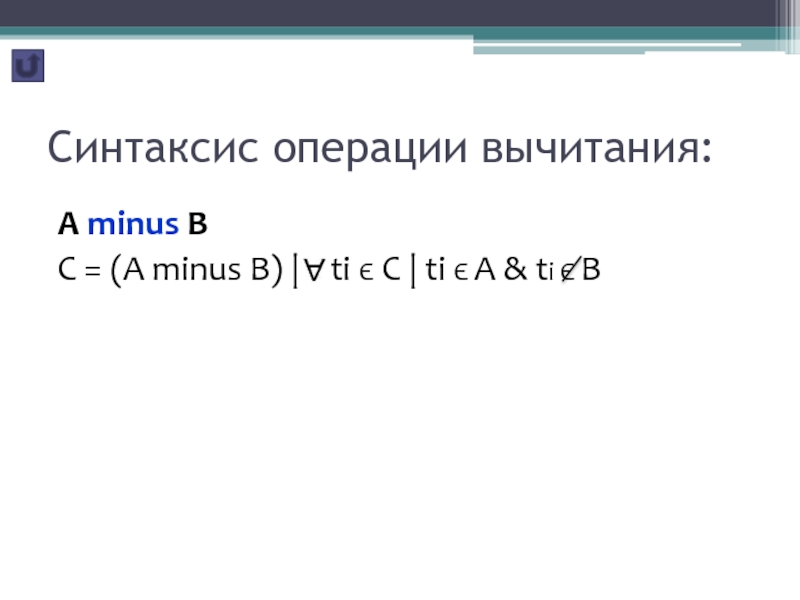
- 13. Синтаксис операции вычитания:A minus BC = (A
- 14. Пример: Для тех же отношений
- 15. Декартово произведение Декартовым
- 16. Синтаксис операции произведения:A times BC = (A
- 17. Пример: Пусть даны два отношения
- 18. Свойства стандартных операций: Операции
- 19. Специальные операцииДеление
- 20. Синтаксис операции деления Отношение
- 21. Пример: Пусть есть отношение исходное АР и
- 22. Выборка
- 23. Синтаксис операции выборки:A where C или A
- 24. Пример: Для отношения А сформируем
- 25. Проекция
- 26. Синтаксис операции проекции:A [X,Y,…,Z]
- 27. Пример: Пусть дано отношение с
- 28. Соединение Операция соединения
- 29. Естественное соединение: Пусть даны
- 30. Синтаксис операции естественного соединения:A JOIN B
- 31. Пример: Пусть имеем таблицу деталей
- 32. Θ - соединение: Пусть отношение
- 33. Скачать презентанцию
Реляционная алгебраВведениеСтандартные операцииСвойства стандартных операцийСпециальные операции
Слайды и текст этой презентации
Слайд 2Реляционная алгебра
Введение
Стандартные операции
Свойства стандартных операций
Специальные операции
Слайд 3 Введение
Реляционная алгебра представляет собой набор операторов,
использующих отношения в качестве аргументов, и возвращающие отношения в качестве результатаТрадиционно, вслед за Коддом, определяют восемь реляционных операторов, объединенных в две группы.
Слайд 6Стандартные реляционные операции
Объединение
Объединением двух совместимых
по типу отношений А и В называется отношение с тем
же заголовком, что и у отношений А и В, и телом, состоящим из кортежей, принадлежащих или А, или В, или обоим отношениям.
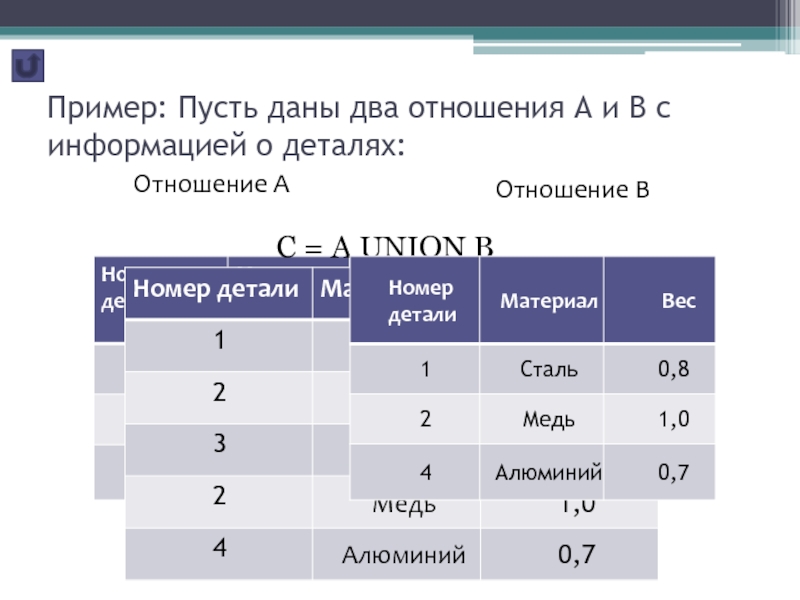
Слайд 8 Пример: Пусть даны два отношения А и В с информацией
о деталях:
Отношение А
С =
A UNION BОтношение В
Слайд 9
Пересечение
Пересечением двух совместимых по типу отношений А и В называется
отношение с тем же заголовком, что и у отношений А и В, и телом, состоящим из кортежей, принадлежащих одновременно обоим отношениям А и В.
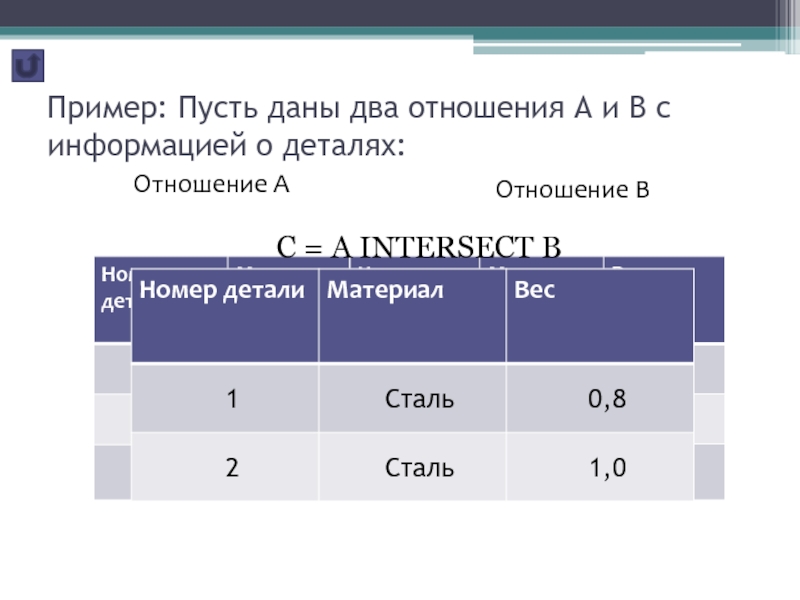
Слайд 11 Пример: Пусть даны два отношения А и В с информацией
о деталях:
Отношение А
С
= A INTERSECT BОтношение В
Слайд 12
Вычитание
Вычитанием двух совместимых по
типу отношений А и В называется отношение с тем же
заголовком, что и у отношений А и В, и телом, состоящим из кортежей, принадлежащих отношению А и не принадлежащих отношению В.
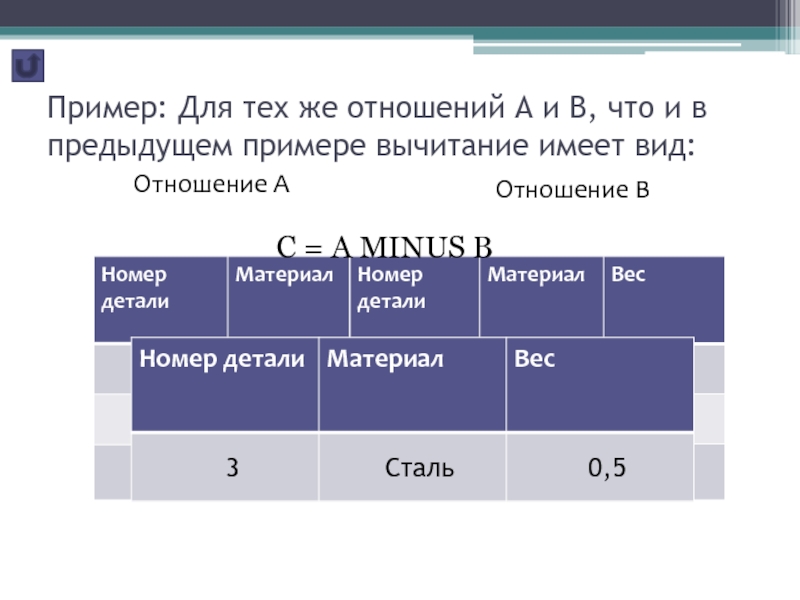
Слайд 14 Пример: Для тех же отношений A и B, что и
в предыдущем примере вычитание имеет вид:
Отношение АС = A MINUS B
Отношение В
Слайд 15
Декартово произведение
Декартовым произведением двух отношений
А(А1, А2, …, Аn) и В(В1, В2, …, Вn) называется
отношение, заголовок которого является сцеплением заголовков отношений А и В, а тело состоит из кортежей, являющихся сцеплением кортежей отношений А и В таких, что (а1, а2, …, аn) Є A, (b1, b2, …, bn) Є B.
Слайд 16Синтаксис операции произведения:
A times B
C = (A times B) |
ai Є A & bi Є
B & ai ≠ bi t | t = ab
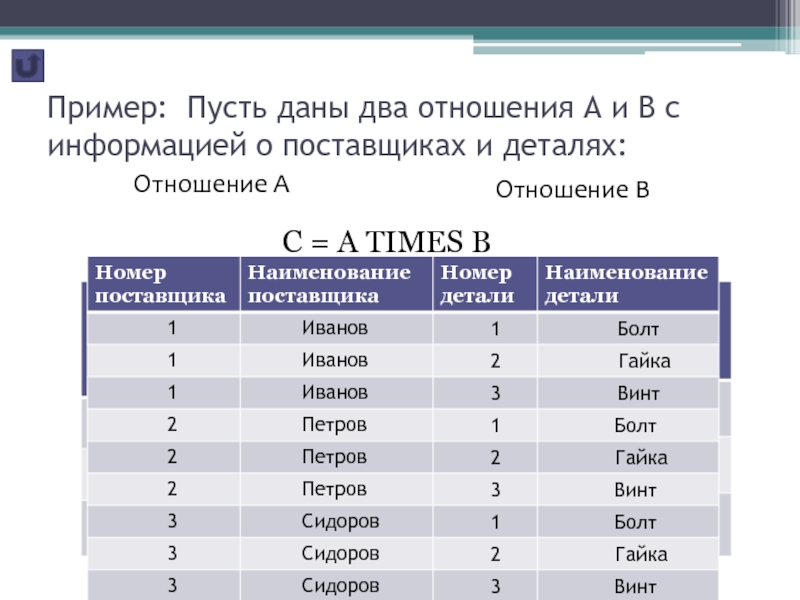
Слайд 17 Пример: Пусть даны два отношения А и В с информацией
о поставщиках и деталях:
Отношение
АОтношение В
С = A TIMES B
Слайд 18Свойства стандартных операций:
Операции объединения, пересечения и
декартова произведения обладают свойствами:
ассоциативность:
(A union B) union C ~ A
union (B union C) => A union B union C; коммутативность;
A union B ~ B union A;
A intersect B ~ B intersect A;
A times B ~ B times A
Указанные свойства не выполняются для операции вычитания.
Слайд 19Специальные операции
Деление
Делением отношений А
на В называется отношение с заголовком (Х1, Х2, …, Хn)
и телом, содержащим множество кортежей (x1, x2, …, xn), таких, что для всех кортежей (y1, y2, …, yn) Є B в отношении A найдется кортеж (x1, x2, …, xn, y1, y2, …, yn).
Слайд 20Синтаксис операции деления
Отношение A выступает в
роли делимого, отношение B выступает в роли делителя. Деление отношений
аналогично делению чисел с остатком.A divide by B
Замечание: Типичные запросы, реализуемые с помощью операции деления, обычно в своей формулировке имеют слово "все" - "какие поставщики поставляют все детали?".
Слайд 21Пример: Пусть есть отношение исходное АР и делители Вi для
i = 1, 2, 3.
АР
В1
AP divide by B1
В2
AP divde
by B2
Слайд 22
Выборка
Выборкой (ограничением, селекцией) на отношении A
с условием C называется отношение с тем же заголовком, что и у отношения A, и телом, состоящем из кортежей, значения атрибутов которых при подстановке в условие C дают значение ИСТИНА. C представляет собой логическое выражение, в которое могут входить атрибуты отношения A и (или) скалярные выражения.
Слайд 23Синтаксис операции выборки:
A where C или A where X Θ
Y
В простейшем случае условие C
имеет вид X Θ Y, где Θ - один из операторов сравнения, а X и Y - атрибуты отношения A или скалярные значения. Такие выборки называются Θ-выборки (тэта-выборки) или Θ-ограничения, Θ-селекции.
Слайд 25
Проекция
Проекцией отношения
A по атрибутам X,Y,…,Z, где каждый из атрибутов принадлежит отношению
A, называется отношение с заголовком (X,Y,…,Z) и телом, содержащим множество кортежей вида (x,y,…,z), таких, для которых в отношении A найдутся кортежи со значением атрибута X равным x, значением атрибута Y равным y, …, значением атрибута Z равным z.
Слайд 26Синтаксис операции проекции:
A [X,Y,…,Z]
Замечание. Операция проекции
дает "вертикальный срез" отношения, в котором удалены все возникшие при
таком срезе дубликаты кортежей.
![Синтаксис операции проекции:A [X,Y,…,Z] Замечание. Операция проекции дает](/img/thumbs/761292a5b7f16a7fbe4e9c37336a667c-800x.jpg "Реляционная алгебра Синтаксис операции проекции:A [X,Y,…,Z] Замечание. Операция проекции дает")
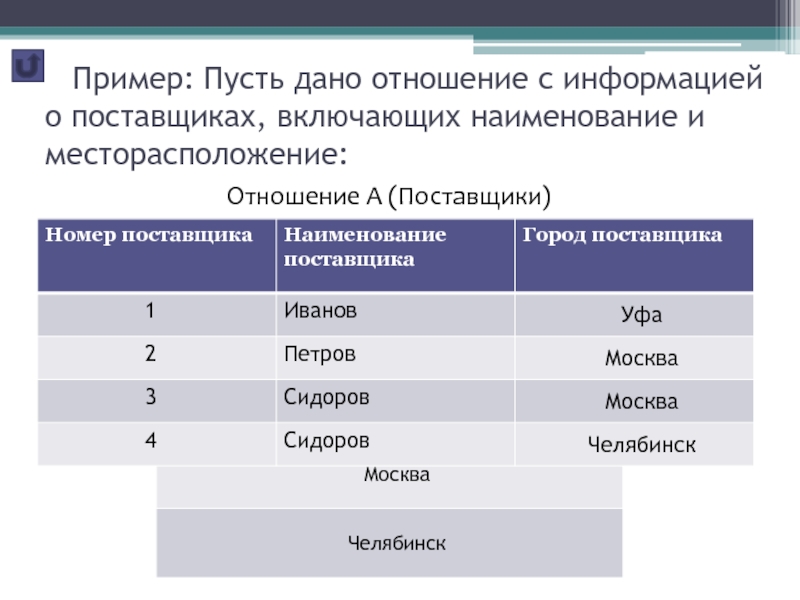
Слайд 27 Пример: Пусть дано отношение с информацией о поставщиках,
включающих наименование и месторасположение:
Отношение А (Поставщики)
Проекция А [Город поставщика]
Слайд 28Соединение
Операция соединения имеет несколько вариантов: это
наиболее важное естественное соединение и Θ-соединение.
Естественное соединение
Θ-соединение
Слайд 29Естественное соединение:
Пусть даны отношения A(A1, A2,…,An, X1,
X2,…, Xp) и B(B1, B2,…,Bn, X1, X2,…,Xm), имеющие одинаковые атрибуты
X1, X2,…, Xp (т.е. атрибуты с одинаковыми именами и определенные на одинаковых доменах).Тогда естественным соединением отношений A и B называется отношение с заголовком A(A1, A2,…,An, X1, X2,…, Xp, B1, B2,…, Bm) и телом, содержащим множество кортежей (a1, a2,…, an, x1, x2,…, xp, b1, b2,…, bm), таких, что (a1, a2,…, an, x1, x2,…, xp) Є A и (x1, x2,…, xp, b1, b2,…, bm) Є B.
Слайд 30Синтаксис операции естественного соединения:
A JOIN B
В
синтаксисе естественного соединения не указываются, по каким атрибутам производится соединение.
Естественное соединение производится по всем одинаковым атрибутам.Можно выполнять последовательное естественное соединение нескольких отношений.
Слайд 31
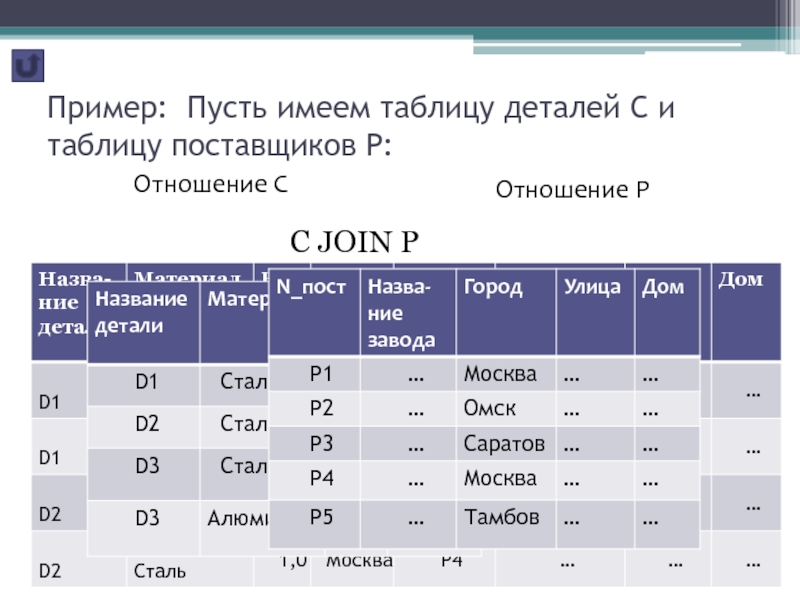
Пример: Пусть имеем таблицу деталей С и таблицу поставщиков Р:
Отношение С
Отношение Р
С JOIN
Р
Слайд 32Θ - соединение:
Пусть отношение А содержит атрибут
Х, отношение В содержит атрибут Y, а Θ - один
из операторов сравнения (=, <, > и т.д.). Тогда Θ - соединением отношения A по атрибуту X с отношением B по атрибуту Y называют отношение:(A TIMES B) WHERE X Θ Y
