Слайд 11. Системы и их моделирование
Слайд 21.1. Моделирование объекта
Применение вычислительных машин и математизация наук привели к
необходимости построения математических моделей объектов, явлений, процессов.
Моделью называется описание, изображение
изучаемого объекта, явления, процесса (далее просто объекта) некоторым способом с целью его изучения.
Иногда моделью называют упрощенную копию объекта. Это не совсем точно, например, при изучении поведения животного. Копия поведения?
Слайд 3Моделирование объекта
Модель всегда описывает объект не полностью, не учитывая несущественные
для исследования детали.
Если объект описан простым разговорным языком, без описания
технических деталей и взаимосвязей, то такая модель называется вербальной.
Если построена физическая копия объекта, то такая модель называется натурной.
Если заданы графики взаимосвязей параметров объекта, то такая модель называется графической.
Слайд 4Моделирование объекта
Если объект описан формальными математическими соотношениями (описаны взаимосвязи параметров),
то это математическая модель объекта.
Математическая модель может иметь конкретное названия
в зависимости от применяемого аппарата. Например, модель в виде дифференциального уравнения, стохастическая модель.
В этом курсе мы будем рассматривать только математические модели.
Слайд 5Моделирование объекта
Для математического моделирования объекта выбираются существенные параметры объекта.
Параметры объекта
– это числа или переменные величины, принимающие числовые значения. Параметры
могут быть управляемыми или неуправляемыми. Управляемые параметры – это переменные величины, исследователь может выбирать значения управляемых параметров. Неуправляемые параметры – это числа или переменные величины, исследователь не может изменять их значения.
Слайд 6Моделирование объекта
При построении аналитической модели строятся математические соотношения между параметрами.
Переменные,
входящие в модель (это управляемые и неуправляемые параметры объекта), могут
быть детерминированными (это обычные переменные из высшей математики) и стохастическими (или случайными – это переменные величины из теории вероятностей и математической статистики). В соответствие с этим модель называется детерминированной или стохастической (случайной).
Слайд 7Моделирование объекта
В радиоэлектронике и радиотехнике большинство моделей стохастические.
Слайд 8Моделирование объекта
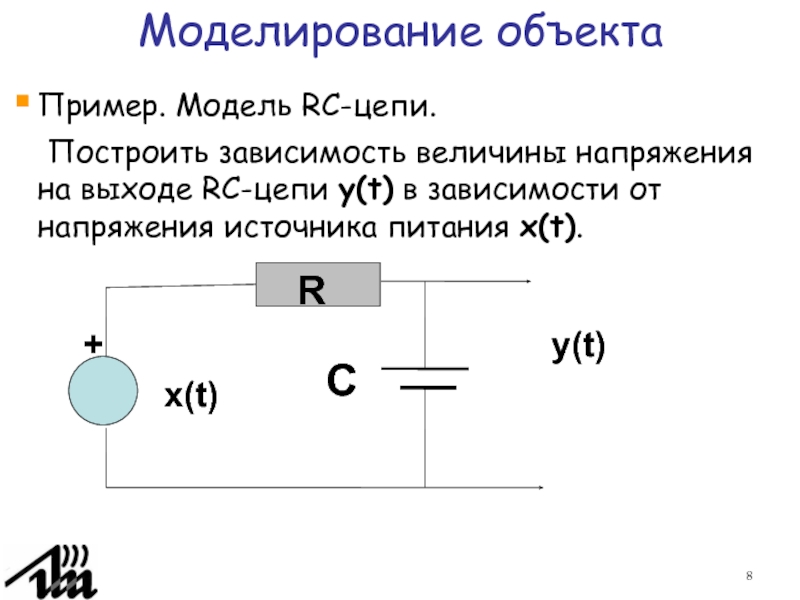
Пример. Модель RC-цепи.
Построить зависимость величины напряжения на выходе RC-цепи
y(t) в зависимости от напряжения источника питания x(t).
R
x(t)
+
C
y(t)
Слайд 9Моделирование объекта
Пример. Модель RC-цепи.
Решение. Параметрами модели будут входящие в схему
величины. Для построения соотношений между ними воспользуемся физическими законами. Пусть
в момент времени t по сопротивлению R проходит ток i(t), а количество электричества на конденсаторе C равно Q(t). Тогда падение напряжения на сопротивлении равно R * i(t), а на конденсаторе y(t) = Q(t)/C .
Слайд 10Моделирование объекта
Пример. Модель RC-цепи.
Решение.
Тогда очевидно соотношение
x(t) = R *
i(t) + y(t). (1)
Кроме того, i(t)
= dQ(t)/dt = d(y(t)*C)/dt = C * y’(t).
Отсюда получаем окончательное соотношение в виде дифференциального уравнения:
x(t) = С*R * y’(t) + y(t).
Слайд 11Моделирование объекта
y(t) + С R y’(t) = x(t)
-это линейное
дифференциальное уравнение первого порядка. Общий вид
y(t) + p(t) y’(t) =
f(t) (*).
Его решение :
где y1(t) – некоторое частное решение уравнения (*).
Решение для исходного уравнения :
Константы c1 и c2 получаем из начальных условий уравнения.
Слайд 121.2. Моделирование системы
В реальной жизни исследуемый объект состоит из множества
связанных между собой объектов, процессов, явлений, объединенных единой целью. Такой
сложный объект будем называть системой, а его части назовем компонентами. При первом рассмотрении можно рассматривать систему как простой объект, не принимая во внимание менее существенные взаимосвязи.
Пример. Производственной предприятие терпит убытки, требуется провести его реструктуризацию.
Слайд 13Моделирование системы
При начальном рассмотрении можно принять во внимание только материалы,
комплектующие, энергетические затраты производства, подсчитать их долю в стоимости продукции
и сравнить эти доли с аналогичными затратами конкурентов. Если этот анализ не дает результата, то хорошим продолжением считается рассмотрение предприятия как системы, состоящей из взаимосвязанных компонент. Разумно в качестве компонент рассматривать административные отделы предприятия: администрация, отдел кадров, бухгалтерия, плановый отдел, отдел снабжения, отдел маркетинга, цеха предприятия и т.п.
Далее следует изучить деятельность каждого отдела в отдельности, а затем работу отделов во взаимосвязи.
Слайд 14Моделирование системы
При анализе системы обычно не строится общая модель системы
– это трудно, а также трудно анализировать такую модель. Строятся
отдельные модели ее компонент и учитываются существенные взаимосвязи между компонентами. Такой подход в моделировании называется декомпозицией.
Построение общей модели системы без декомпозиции практически невозможно: компоненты системы разнородны и их трудно описать в рамках одной математической теории.
Пример. Технологический процесс производства азота описывается уравнениями химических реакций, а работа отдела снабжения графами связей с поставщиками.
Примечание. Рассмотренная задача анализа производства в современном менеджменте называется задачей консалтинга.
Слайд 15Моделирование системы
Пример системы. Стропы и ткань. Соединенные специальным образом, они
образуют новый объект – парашют со свойствами, которыми не обладают
исходные предметы. Можно изучить свойства строп и ткани по отдельности (прочность, воздухопроницаемость, …), но существенным будет схема соединения этих компонент и способ укладки парашюта.
Слайд 16Моделирование системы
Модель отражает цель исследования
Слайд 17Моделирование системы
Решение задачи начинается с ее постановки, то есть с
определения объекта исследования, формулировки цели и построения математической модели. Говорят,
что хорошая постановка задачи на 50% уже решает задачу. В нашем изложении основной частью постановки задачи является моделирование.
Часто компоненты системы имеют несовпадающие или даже противоположные цели. В этом случае исследователь должен согласовать их. В процессе исследования цели могут уточняться, при этом некоторые параметра могут оказаться несущественными, а другие введены в модель как существенные. То есть, решение задачи – это процесс.
Слайд 18Моделирование системы
Системный подход - комплексное изучение объекта как единого целого
путем уточнение задачи и её декомпозицию в серию задач, решаемых
с помощью методов естественных наук. При решении задач детализируются цели исследования, формализуются критерии сравнения решений, выбираются или строятся методы достижения целей.
Слайд 19Моделирование системы
Системотехника - прикладная наука, исследующая задачи создания сложных управляющих
систем. Процесс построения системы состоит из шести этапов:
1) Изучение функционирования
системы.
2) Определение целей, составление графиков и планов работы (системное программирование).
3) Проектирование системы, её компонент для достижения поставленных целей (системное проектирование).
4) Создание программного обеспечения.
5) Тестирование системы и ее ввод в действие.
6) Обслуживание и поддержка системы.
Это комплексная задача, ее решает команда из представителей разных специальностей. При участии в современных разработках важно уметь работать в команде.
Слайд 20Моделирование системы
При участии в современных разработках важно уметь работать в
команде.
Команда для решения системных задач