Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 Эйлер, Ляпунов, Навье и Стокс
Содержание
- 1. 1 Эйлер, Ляпунов, Навье и Стокс
- 2. 1. Уравнение Фридмана и Гельмгольца2. Можно ли
- 3. Комплексная скоростьикомплексный потенциалw=+i
- 4. хiy1iПостроить отрезок [(1, i),(3, 2i)]Рассмотрим комплексную плоскость (х,у) Точка на плоскости определяется комплексным числом
- 5. х1iyiПостроить отрезок [(1, i),(3, 2i)]232iПостроить отрезок [(1,i),(2,-2i)]
- 6. Зададим комплексную функции w=f(z)
- 7. Тогда уравнения справа – условия Коши-Римана для
- 8. Это значит, что функция w=f(z) имеет определенную производнуюux-uy
- 9. Производная комплексной функции
- 10. D = x(x0,y0)D x + y(x0,y0)D y +x (x,y);D = x(x0,y0)D x+ y(x0,y0)D y + h (x,y);V(x,y)=x (x,y)+ih (x,y)
- 11. Слайд 11
- 12. Функция w=+i называется комплексным потенциалом, однозначно определяет плоское течение- комплексная скоростьuхiuy
- 13. Пример №1Задан комплексный потенциалa – действительная величина, константаОпределить линии тока, линии равного потенциала, поле скорости
- 14. Пример №1
- 15. хyЛиния токаПример №1На линии тока функция тока сохраняет постоянное значение
- 16. Найти поток скорости через отрезок z1=(1,0) z2=(0,i)
- 17. хiy1iАВ
- 18. хiyi1Энергия объема, заключенного внутри контура [(1,0), (1,i), (0,i), (0,0)](1, i)
- 19. хiyi1(1, i)Энергия объема, заключенного внутри контура [(1,0), (1,i), (0,i), (0,0)]
- 20. Пример №2a, b – вещественныеНайти: потенциал скорости, функцию тока, скорость, комплексную скорость, линии тока
- 21. Пример №2uxuyux=a-b
- 22. Пример №2iuyabux
- 23. Пример №2вдоль линии токаЛинии тока определены как:хiyab = const
- 24. Пример №2Найти поток через отрезок [(0), (a,
- 25. Найти поток через отрезок [(0), (a, -bi)]Пример №2хiyab = constПоток вдоль линии тока равен 0
- 26. Найти энергию объема, ограниченного контуром [(1, i),
- 27. Пример №3Найти потенциал скорости, функцию тока, компоненты скорости
- 28. Пример №3
- 29. Пример №3Найти линии токаВектор скорости нарисоватьНарисовать вектор комплексной скоростиМожно ли заменить оси координат твердыми стенками?
- 30. Пример №3хyЛинии х=0 и у=0 являются частями одной и той же линии тока =0.z
- 31. Пример №3Нарисовать линии равного потенциала
- 32. Пример №3yна линии равного потенциалах
- 33. Пример №3Найти поток скорости через отрезок [(0,i),(1,0)]
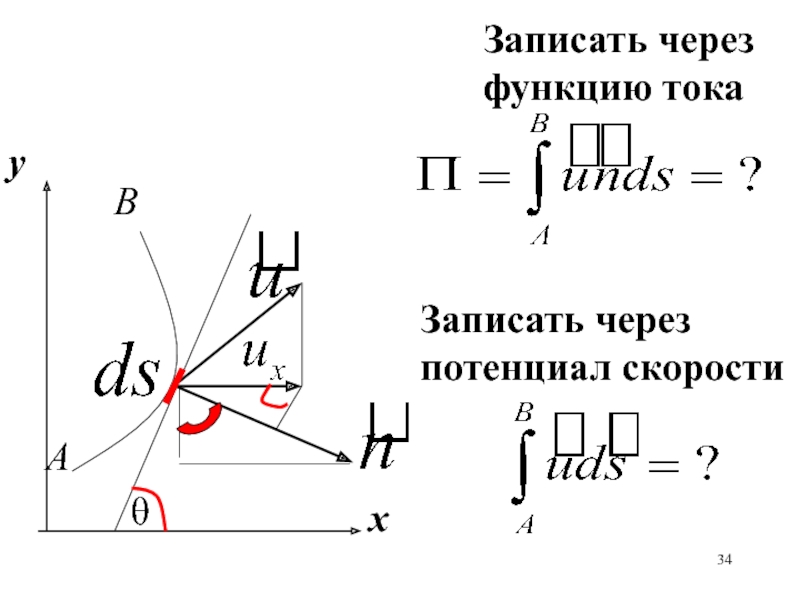
- 34. ABхуЗаписать через функцию токаЗаписать через потенциал скорости
- 35. Слайд 35
- 36. Записать скорости течения через функцию токаКак меняется
- 37. Скачать презентанцию
1. Уравнение Фридмана и Гельмгольца2. Можно ли вызвать движение неподвижной идеальной жидкости, если приложить постоянное давление по всему объему? Почему?Контрольная работа
Слайды и текст этой презентации
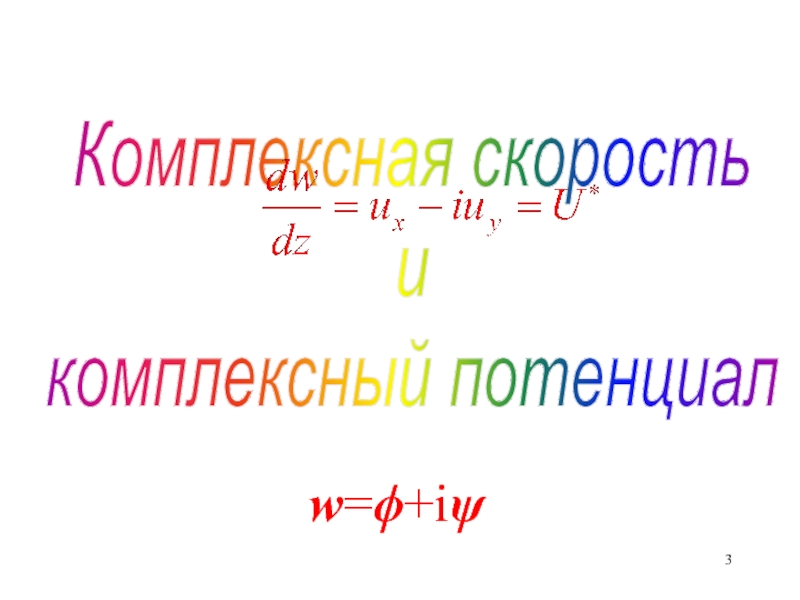
Слайд 21. Уравнение Фридмана и Гельмгольца
2. Можно ли вызвать движение неподвижной
идеальной жидкости, если приложить постоянное давление по всему объему? Почему?
работа
Слайд 4х
iy
1
i
Построить отрезок [(1, i),(3, 2i)]
Рассмотрим комплексную плоскость (х,у) Точка на
плоскости определяется комплексным числом
![хiy1iПостроить отрезок [(1, i),(3, 2i)]Рассмотрим комплексную плоскость (х,у) Точка на плоскости определяется комплексным числом](/img/thumbs/b056293f29204f5086d60351c743fad0-800x.jpg "1
Эйлер, Ляпунов, Навье и Стокс хiy1iПостроить отрезок [(1, i),(3, 2i)]Рассмотрим комплексную плоскость (х,у) Точка на плоскости определяется комплексным числом")
![х1iyiПостроить отрезок [(1, i),(3, 2i)]232iПостроить отрезок [(1,i),(2,-2i)]](/img/thumbs/1dcd558d02ce11cc7ef5d31f6927ecba-800x.jpg "1
Эйлер, Ляпунов, Навье и Стокс х1iyiПостроить отрезок [(1, i),(3, 2i)]232iПостроить отрезок [(1,i),(2,-2i)]")
Слайд 7Тогда уравнения справа – условия Коши-Римана для и
представляют собой условия аналитичности функции w=f(z) комплексного аргумента z=x+iy
Слайд 10D = x(x0,y0)D x + y(x0,y0)D y +x (x,y);
D = x(x0,y0)D x+
y(x0,y0)D y + h (x,y);
V(x,y)=x (x,y)+ih (x,y)
Слайд 12Функция w=+i называется комплексным потенциалом, однозначно определяет плоское течение
- комплексная
скорость
uх
iuy
Слайд 13Пример №1
Задан комплексный потенциал
a – действительная величина, константа
Определить линии тока,
линии равного потенциала, поле скорости
Слайд 16Найти поток скорости через отрезок z1=(1,0) z2=(0,i)
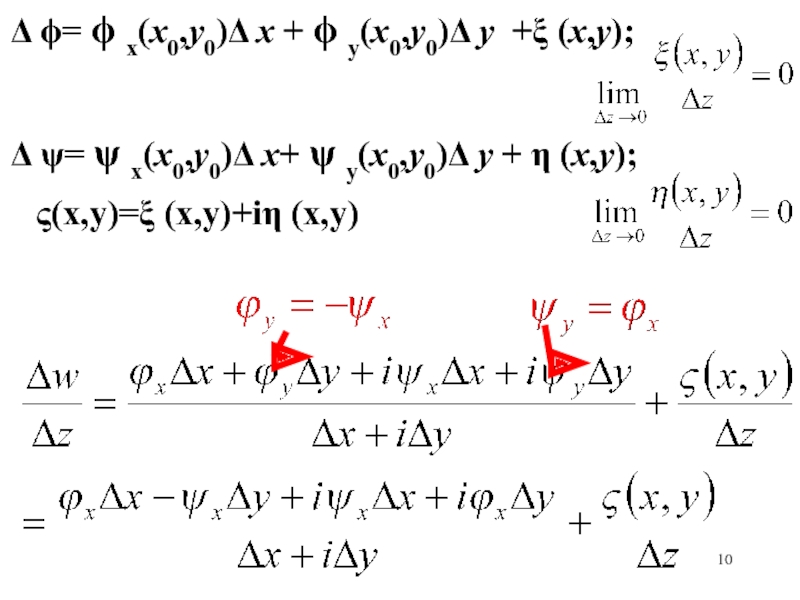
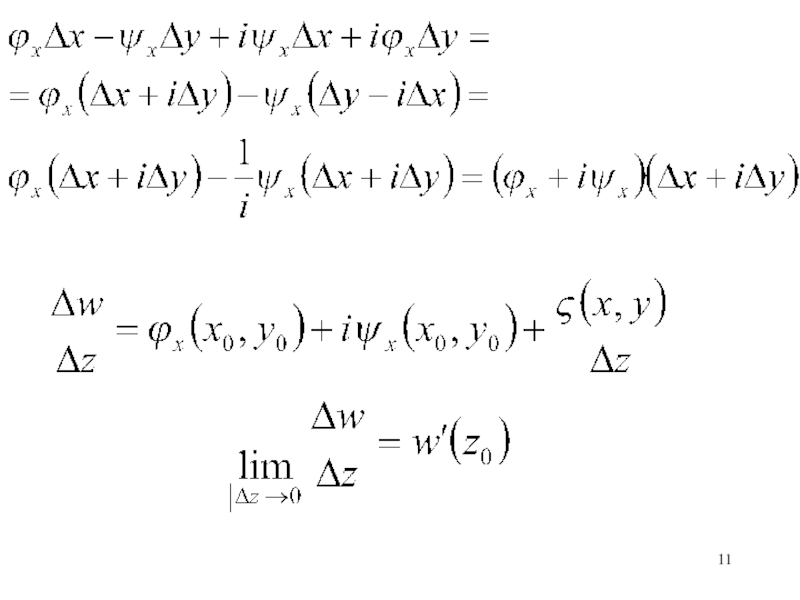
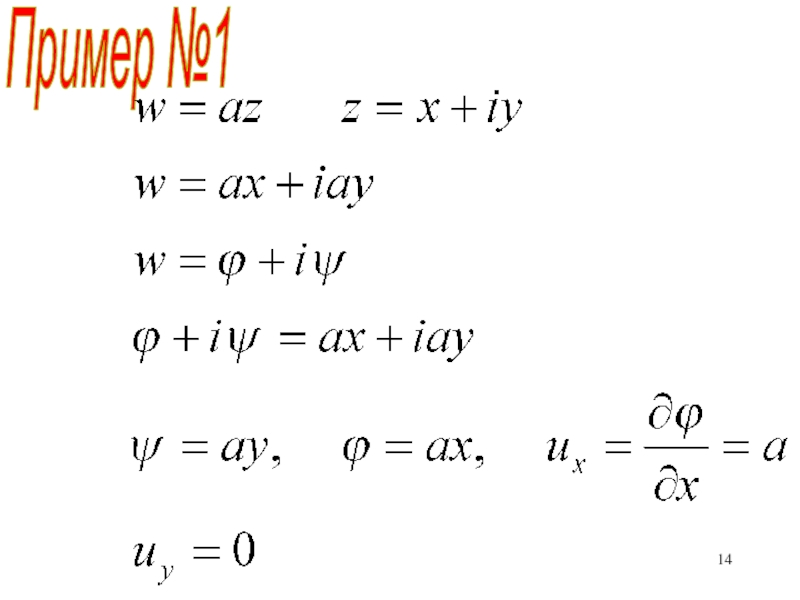
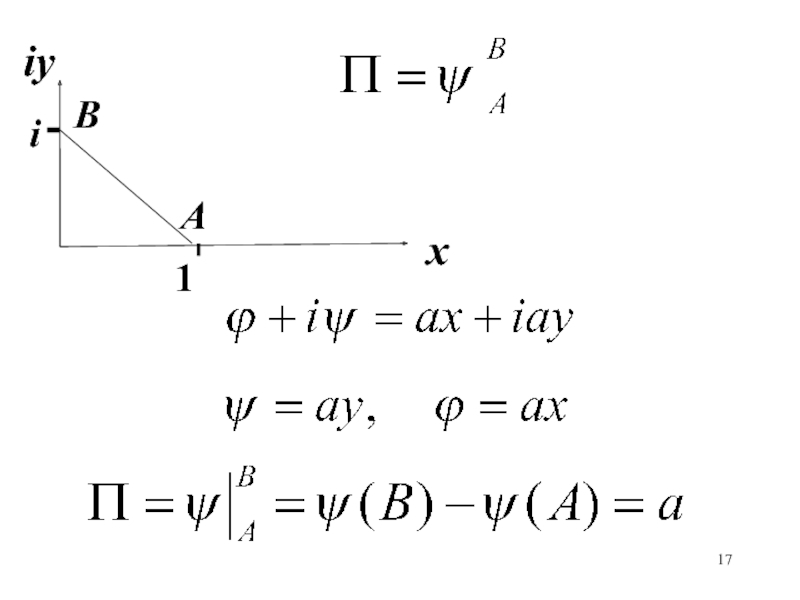
Найти энергию объема,
заключенного внутри контура [(1,0), (1, i), (0,i), (0,0)]
Пример №1
](/img/thumbs/3e644e90444509248829662516c0ea44-800x.jpg "1
Эйлер, Ляпунов, Навье и Стокс хiyi1Энергия объема, заключенного внутри контура [(1,0), (1,i), (0,i), (0,0)](1, i)")
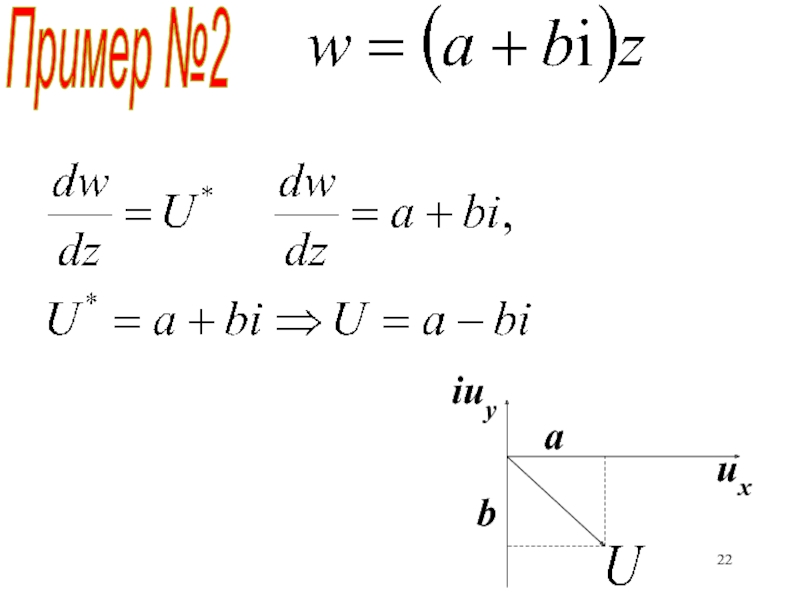
![хiyi1(1, i)Энергия объема, заключенного внутри контура [(1,0), (1,i), (0,i), (0,0)]](/img/thumbs/bfdffcdc1c870d7e5a77ae690d82ee43-800x.jpg "1
Эйлер, Ляпунов, Навье и Стокс хiyi1(1, i)Энергия объема, заключенного внутри контура [(1,0), (1,i), (0,i), (0,0)]")
Слайд 20Пример №2
a, b – вещественные
Найти: потенциал скорости, функцию тока, скорость,
комплексную скорость, линии тока
Слайд 24Пример №2
Найти поток через отрезок [(0), (a, -bi)]
Найти энергию объема,
ограниченного контуром [(1. i), (-1. i). (-1. -i), (1. -i)]
Найти
циркуляцию скорости по этому контуру![Пример №2Найти поток через отрезок [(0), (a, -bi)]Найти энергию объема, ограниченного контуром [(1. i), (-1. i). (-1.](/img/thumbs/7dffb89980544434d4cbaff59154a34a-800x.jpg "1
Эйлер, Ляпунов, Навье и Стокс Пример №2Найти поток через отрезок [(0), (a, -bi)]Найти энергию объема, ограниченного")
Слайд 25Найти поток через отрезок [(0), (a, -bi)]
Пример №2
х
iy
a
b
= const
Поток
вдоль линии тока равен 0
![Найти поток через отрезок [(0), (a, -bi)]Пример №2хiyab = constПоток вдоль линии тока равен 0](/img/thumbs/1ee0df76be8695093e07407857f8ecc4-800x.jpg "1
Эйлер, Ляпунов, Навье и Стокс Найти поток через отрезок [(0), (a, -bi)]Пример №2хiyab = constПоток вдоль линии тока равен 0")
Слайд 26Найти энергию объема, ограниченного контуром [(1, i), (-1, i). (-1,
-i), (1, -i)]
Пример №2
х
(-1, i)
(1, i)
(-1, -i)
(1, -i)
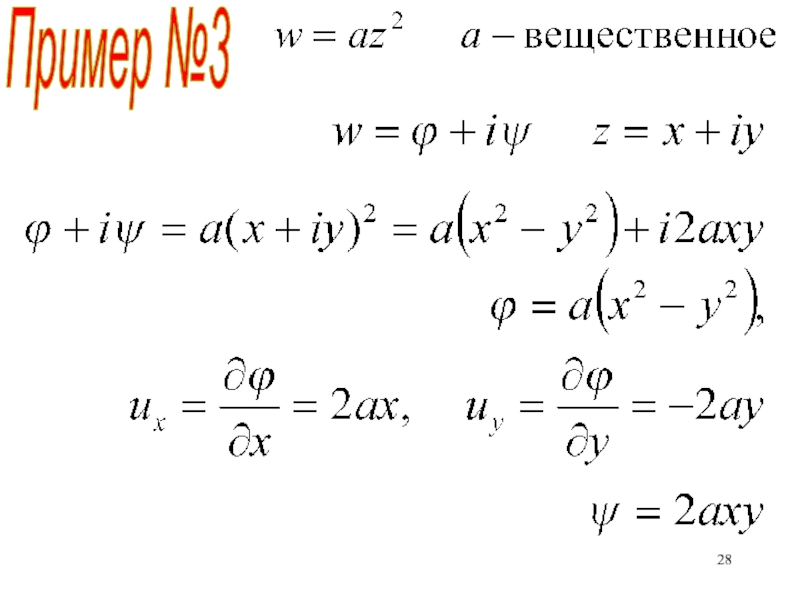
![Найти энергию объема, ограниченного контуром [(1, i), (-1, i). (-1, -i), (1, -i)]Пример №2х(-1, i)(1, i)(-1, -i)(1,](/img/thumbs/4d9e68f5150729918c6eb7ec7c53c565-800x.jpg "1
Эйлер, Ляпунов, Навье и Стокс Найти энергию объема, ограниченного контуром [(1, i), (-1, i). (-1, -i),")
Слайд 29Пример №3
Найти линии тока
Вектор скорости нарисовать
Нарисовать вектор комплексной скорости
Можно ли
заменить оси координат твердыми стенками?
![Пример №3Найти поток скорости через отрезок [(0,i),(1,0)]](/img/thumbs/c0b33c636c17d1ffa6edc2dcdb361225-800x.jpg "1
Эйлер, Ляпунов, Навье и Стокс Пример №3Найти поток скорости через отрезок [(0,i),(1,0)]")
Слайд 36Записать скорости течения через функцию тока
Как меняется функция тока вдоль
линии тока?
Условие аналитичности функции w=+i комплексного аргумента z=x+iy
Написать выражение
комплексной скорости
