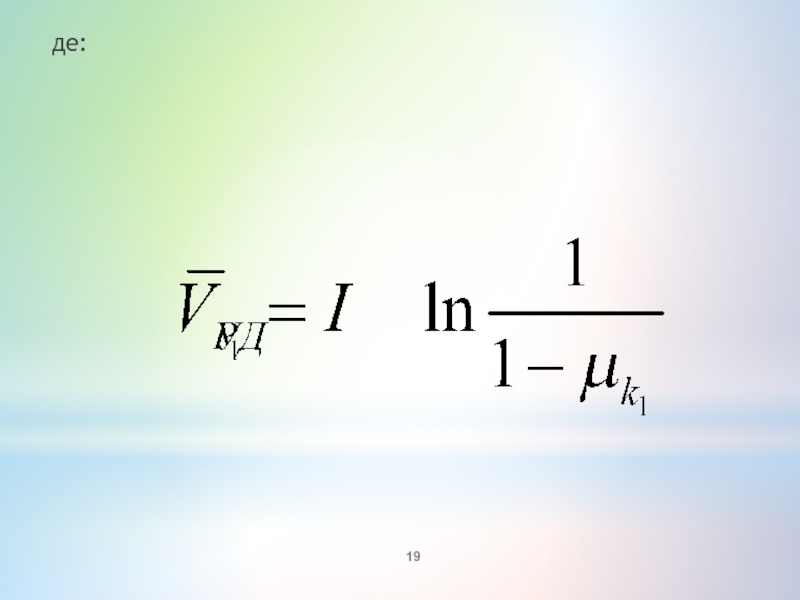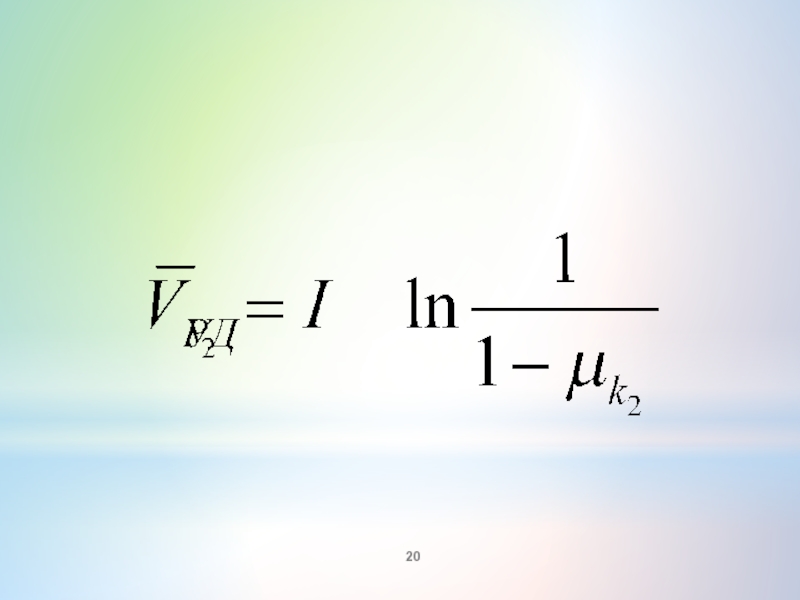Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 Групове заняття з предмету “ Конструкція ракет ” Тема 2 Основи теорії польоту
Содержание
- 1. 1 Групове заняття з предмету “ Конструкція ракет ” Тема 2 Основи теорії польоту
- 2. 1. Розрахунок ідеальної та дійсної швидкості одноступеневої ракети.2. Розрахунок ідеальної та дійсної швидкості багатоступеневої ракети.
- 3. Узагальнити та закріпити знання щодо розрахунку ідеальної
- 4. ЛІТЕРАТУРАДмитрієвський А.А. Движениє ракет. 1968 с.123-134.Дегтярева
- 5. Перше питання заняття – Розрахунок ідеальної та дійсної швидкості одноступеневої ракети.
- 6. Для закріплення отриманих на груповому занятті знань,
- 7. РішенняПеред розрахунками швидкостей значення тяги
- 8. Як відомо, ідеальна швидкість одноступеневої ракети розраховується за формулою:
- 9. Розрахуємо спочатку питомий імпульс тяги ракетного двигуна (Іуд):
- 10. Тепер для проведення подальших розрахунків знайдемо коефіцієнт наповнення ракети 8К14 паливом:
- 11. Як бачимо, коефіцієнт для ракети не
- 12. Отримані у розрахунках результати підставимо у формулу
- 13. Тепер розрахуємо дійсну швидкість даної ракети.Як відомо,
- 14. Для одноступеневих ракет витрати швидкості складають приблизно (18 – 25%) від ідеальної швидкості, тобто:
- 15. Враховуючи це, розрахуємо приблизне значення дійсної швидкості
- 16. Розрахунок ідеальної та дійсної швидкості багатоступеневої ракети.Друге питання
- 17. Ідеальна швидкість багатоступеневої ракети складається з ідеальних швидкостей ступенів що входять до складу багатоступеневої ракети.
- 18. Наприклад, якщо багатоступенева ракета складається з двох ступенів то отримаємо:
- 19. де:
- 20. Слайд 20
- 21. Коефіцієнти наповнення багатоступеневої ракети паливом визначаються за наступними формулами:
- 22. де m0 = m01 + m02;
- 23. Якщо питомі імпульси двигунів (
- 24. Розрахуємо яку максимальну швидкість отримала б ракета
- 25. Розрахуємо коефіцієнти наповнення паливом (
- 26. Підставимо отримані значення
- 27. При порівнянні максимальних швидкостей одноступеневої та двохступеневої
- 28. Це виникає тому, що збільшення числа ступенів
- 29. Скачать презентанцию
1. Розрахунок ідеальної та дійсної швидкості одноступеневої ракети.2. Розрахунок ідеальної та дійсної швидкості багатоступеневої ракети.
Слайды и текст этой презентации
Слайд 1Групове заняття з предмету “ Конструкція ракет ”
Тема 2
Основи теорії польоту ракет.
швидкості балістичної ракети.Слайд 2
1. Розрахунок ідеальної та дійсної швидкості одноступеневої ракети.
2. Розрахунок ідеальної
та дійсної швидкості багатоступеневої ракети.
Слайд 3Узагальнити та закріпити знання щодо розрахунку ідеальної та дійсної швидкості
одноступеневої та багатоступеневої балістичної ракети, а також знання щодо розрахунку
елементів її траєкторії. Мета заняття
Слайд 4
ЛІТЕРАТУРА
Дмитрієвський А.А. Движениє ракет. 1968 с.123-134.
Дегтярева В.Б. Системи автоматического управления
ЛА. 1988 с. 40-54.
Поляков А. П. Физические основы ракетного оружия.
1990 с. 92-111.Слайд 6Для закріплення отриманих на груповому занятті знань, розрахуємо максимальну (ідеальну)
та дійсну швидкість оперативно-тактичної ракети
Вихідні данні:
1 Вага повністю заправленої
ракети з ГЧ 8Ф44 - 5860 кг.2 Вага палива та стиснутого повітря - 3786 кг.
3 Тяга ракетного двигуна - 13310 кг.
4 Витрата ракетного палива - 57,83 кг/сек..
Слайд 7 Рішення
Перед розрахунками швидкостей значення тяги ракетного двигуна переведемо
до одиниць міжнародної системи SI, тобто з [кг] у [H]
для чого:Слайд 10Тепер для проведення подальших розрахунків знайдемо коефіцієнт наповнення ракети 8К14
паливом:
Слайд 11Як бачимо, коефіцієнт для ракети не великий. Як відомо,
для сучасних одноступеневих ракет коефіцієнт наповнення ракети паливом лежить у
межах 0,8 – 0,92.Слайд 12Отримані у розрахунках результати підставимо у формулу Ціолковського щодо визначення
ідеальної швидкості польоту одноступеневої ракети:
Це і є максимальна швидкість яку може отримати ракета, яка здійснювала б вертикальний політ у безповітряному просторі при відсутності сили тяжіння та після повної витрати палива.
Слайд 13Тепер розрахуємо дійсну швидкість даної ракети.
Як відомо, дійсна швидкість ракети
менша за ідеальну на величину гравітаційних та аеродинамічних витрат, тобто
:Слайд 14Для одноступеневих ракет витрати швидкості складають приблизно
(18 –
25%) від ідеальної швидкості, тобто:
Слайд 15Враховуючи це, розрахуємо приблизне значення дійсної швидкості оперативно–тактичної ракети враховуючи,
що на гравітаційну та аеродинамічну силу ракета витрачає 25% від
своєї швидкості :Слайд 17Ідеальна швидкість багатоступеневої ракети складається з ідеальних швидкостей ступенів що
входять до складу багатоступеневої ракети.
Слайд 21Коефіцієнти наповнення багатоступеневої ракети паливом визначаються за наступними формулами:
Слайд 22де m0 = m01 + m02;
m01 =
mп1 + mk1; m02 = mп2 + mk2*.
m0 –
повна маса багатоступеневої ракети;m01 – повна маса 1-го ступеню ракети;
m02 – повна маса 2-го ступеню ракети;
mk1 – маса конструкції 1-го ступеню ракети;
mп1 – маса палива 1-го ступеню ракети;
mk2* - маса конструкції 2-го ступеню ракети куди входить маса головної частини ракети (корисного навантаження);
mп2 – маса палива 2-го ступеню ракети.
Слайд 23Якщо питомі імпульси двигунів
( ) на
першому та другому ступеню багатоступеневої ракети рівні, то ідеальну швидкість
можливо отримати за формулою:Слайд 24Розрахуємо яку максимальну швидкість отримала б ракета з двохступеневою схемою
при незмінних характеристиках.
Приклад №2
Вихідні дані :
1 Питомий імпульс двигунів (Іу1,2)
- 2258 м/с 2. Маса палива 1-го та 2-го ступеню - 3786 кг
3 Повна маса 1-го ступеню (m01) - 4873 кг
4 Повна маса 2-го ступеню (m02) - 5860 кг