1 Лекция № 14. Определение продолжительности нагрева термически массивных тел

Определение продолжительности нагрева термически массивных тел. Аналитические методы определения времени нагрева

Для ТМТ неприемлемо допущение о равенстве температур поверхности среднемассовой,

Нагрев считается законченным, когда:

1) температура поверхности равна заданной:

2) конечный перепад температур по толщине меньше или равен заданному:

Если

, то продолжаем нагрев, но при других ГУ.

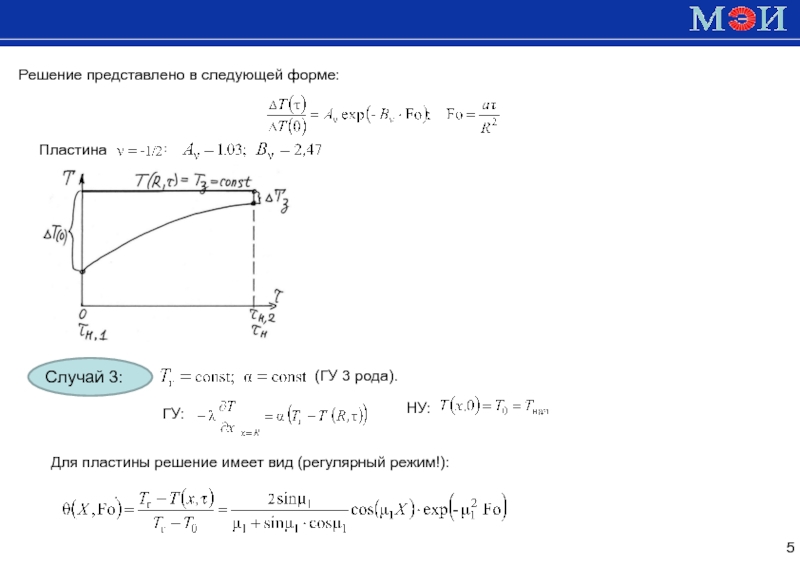
Методы определения времени нагрева

:

1. Аналитическое решение краевой задачи теплопроводности (КЗТ).

2. Приближенные методы определения

.

3. Численные методы решения КЗТ.

периода:

1. ОПРЕДЕЛЕНИЕ ВРЕМЕНИ НАГРЕВА ИЗ АНАЛИТИЧЕСКОГО РЕШЕНИЯ КЗТ

1) Реальные тела сводим к одному из тел правильной формы.

2) Граничные условия однородны по поверхности тела.

В результате этих двух допущений – симметричность и одномерность температурного поля:

3) Физические свойства не зависят от температуры.

4) Начальные и граничные условия описываются простейшими уравнениями.

(в общем случае

).

Следовательно, длительность нагрева приближенно равна длительности регулярного периода:

ТЕПЛОПРОВОДНОСТИ
1. Дифференциальное уравнение теплопроводности Фурье:
2. Геометрические условия задачи:

;

– характерный размер.

3. Физические условия задачи:

4. Начальные и граничные условия. ГУ:

Начальные условия (НУ):

1.3. РЕШЕНИЯ УРАВНЕНИЯ ФУРЬЕ

Случай 1:

(ГУ 2 рода).

по толщине тела:
Скорость подъема температуры во всех точках тела одинакова,

.

Случай 2:

(ГУ 1 рода).

Начальные условия (НУ):

– перепад температур по всему характерному размеру.

следующей форме:
Пластина
:

Случай 3:
(ГУ 3

ГУ:

НУ:

Для пластины решение имеет вид (регулярный режим!):

уравнения