Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
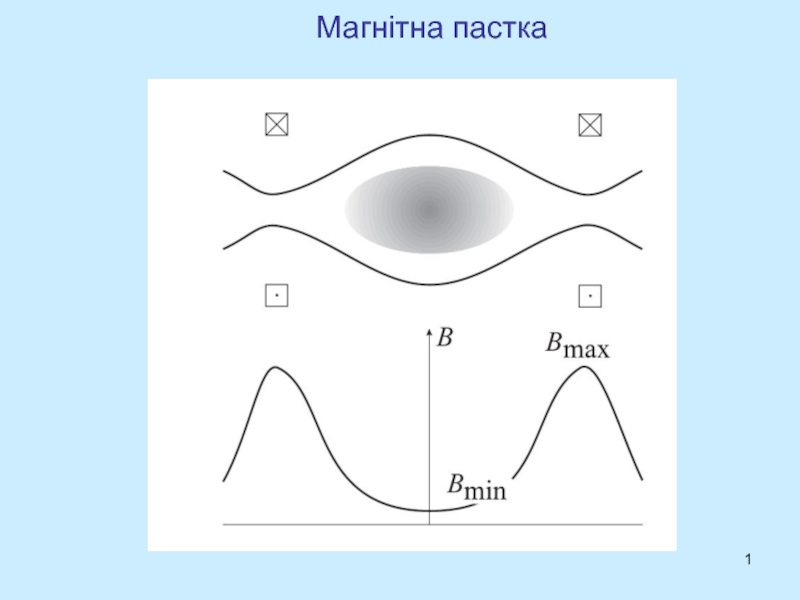
1 Магнітна пастка
Содержание
- 1. 1 Магнітна пастка
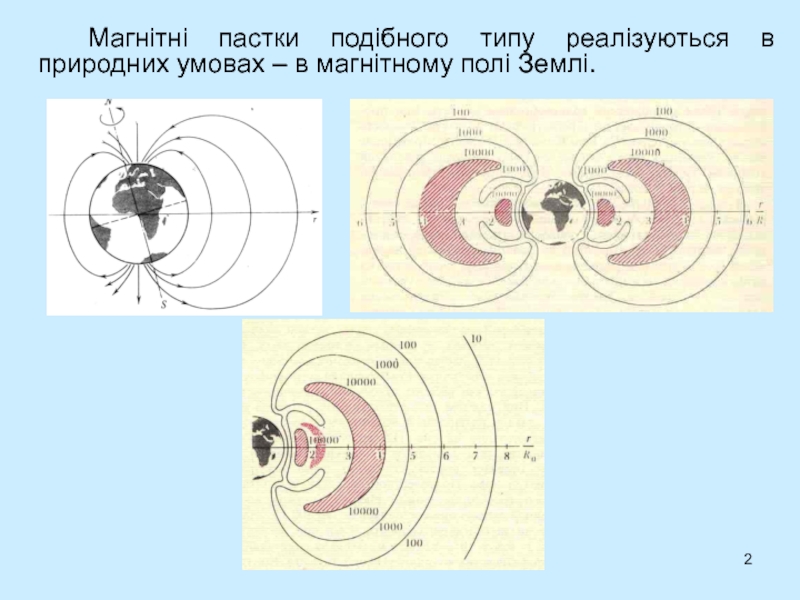
- 2. Магнітні пастки подібного типу реалізуються в природних умовах – в магнітному полі Землі.
- 3. Неоднорідне магнітне поле Магнітне поле, напруженість якого змінюється
- 4. Неоднорідне магнітне поле Магнітне поле, напруженість якого змінюється
- 5. Особливість дрейфового руху: немає зсуву в сторону
- 6. Зміщення траєкторії за один оберт: Середня швидкість дрейфу
- 7. Враховуючи, що для неоднорідного поля, яке слабко
- 8. Дрейфовий рух може бути зумовлений і подовжньою
- 9. В точці М1 вектор
- 10. Швидкість дрейфу за умови довільної орієнтації
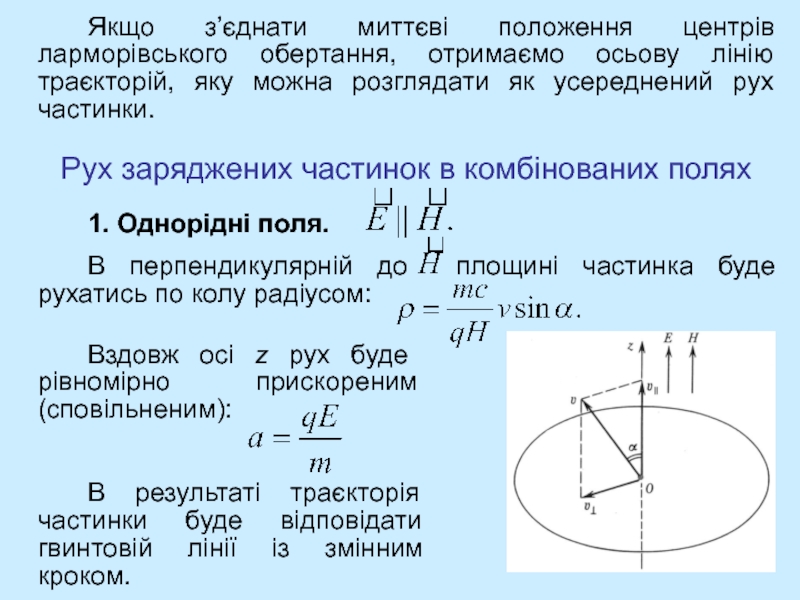
- 11. Якщо з’єднати миттєві положення центрів ларморівського обертання,
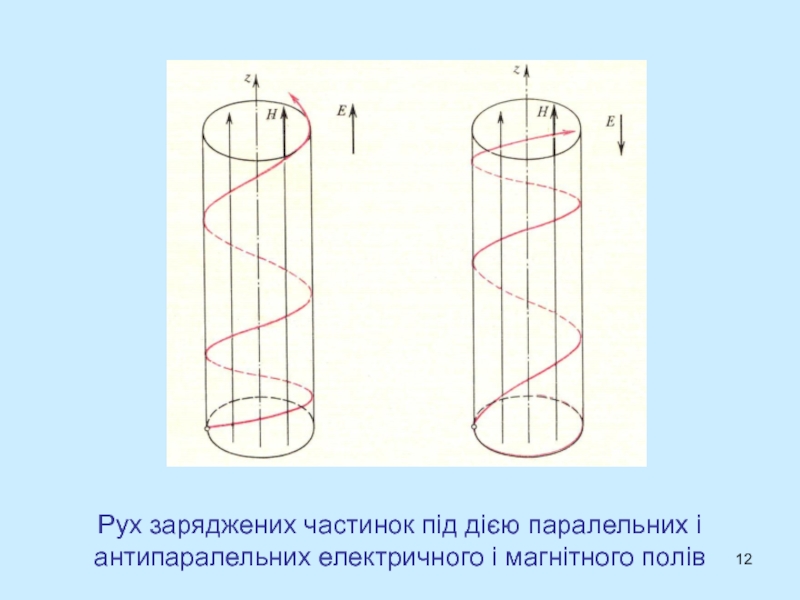
- 12. Рух заряджених частинок під дією паралельних і антипаралельних електричного і магнітного полів
- 13. 2. Однорідні поля. Допустимо, що вісь y
- 14. Система рівнянь матиме вигляд: Таким чином, в новій
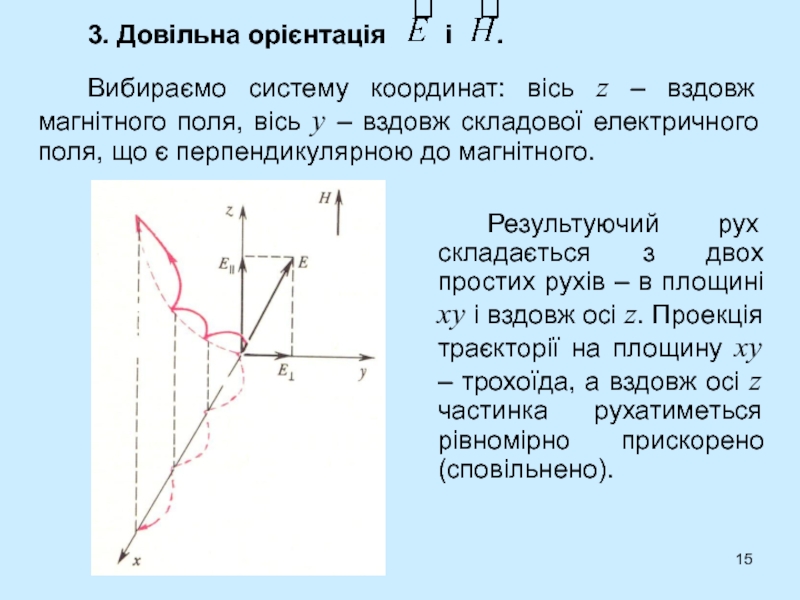
- 15. 3. Довільна орієнтація і
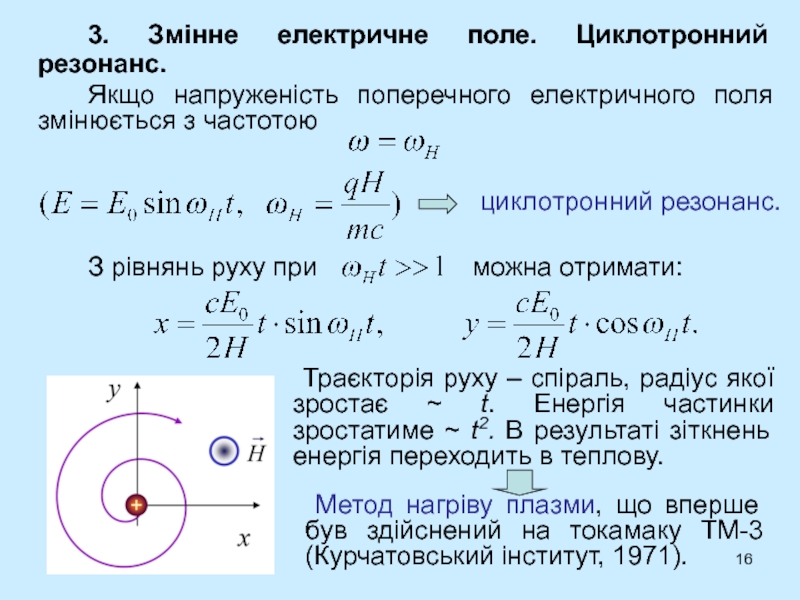
- 16. 3. Змінне електричне поле. Циклотронний резонанс. Якщо напруженість
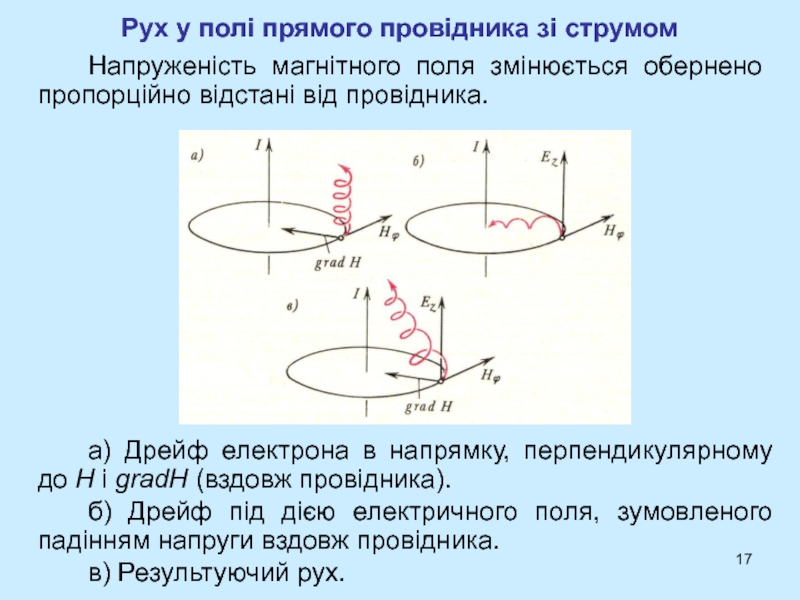
- 17. Рух у полі прямого провідника зі струмом Напруженість
- 18. Вплив магнітного поля на властивості плазми В проміжку
- 19. Критерій замагніченості: де τ – середній час між
- 20. Ситуація, коли електрони є замагніченими, а іони
- 21. Внаслідок зумовлених сильним магнітним полем обмежень на
- 22. Скачать презентанцию
Слайды и текст этой презентации
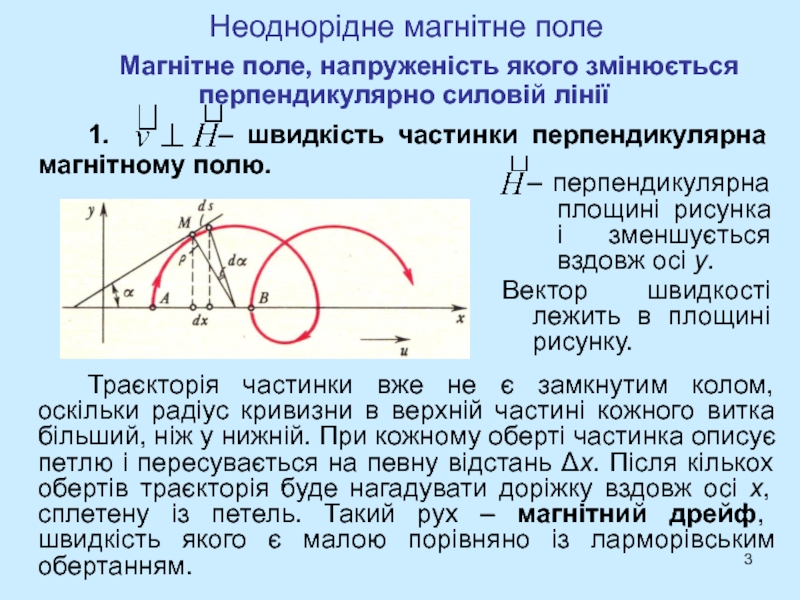
Слайд 3Неоднорідне магнітне поле
Магнітне поле, напруженість якого змінюється перпендикулярно силовій лінії
– перпендикулярна площині рисунка і зменшується вздовж осі y.
Вектор
швидкості лежить в площині рисунку. Траєкторія частинки вже не є замкнутим колом, оскільки радіус кривизни в верхній частині кожного витка більший, ніж у нижній. При кожному оберті частинка описує петлю і пересувається на певну відстань Δх. Після кількох обертів траєкторія буде нагадувати доріжку вздовж осі х, сплетену із петель. Такий рух – магнітний дрейф, швидкість якого є малою порівняно із ларморівським обертанням.
1. – швидкість частинки перпендикулярна магнітному полю.
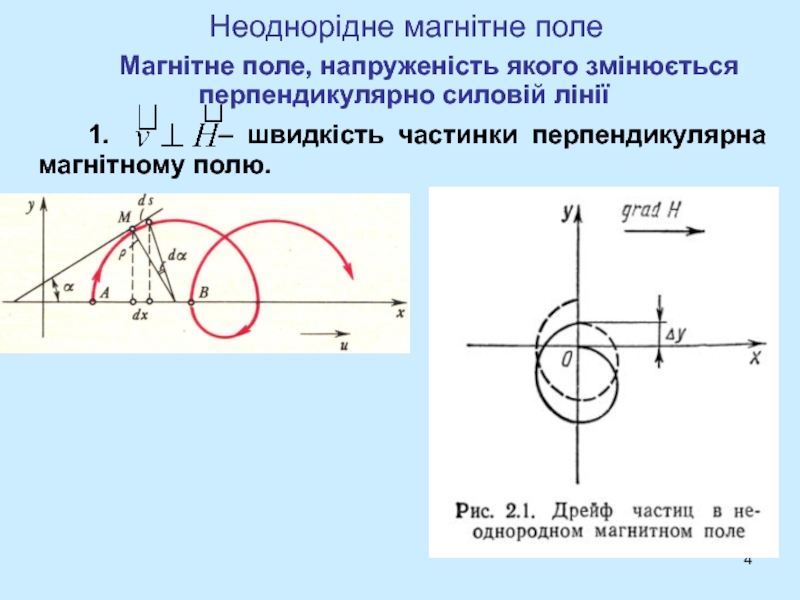
Слайд 4Неоднорідне магнітне поле
Магнітне поле, напруженість якого змінюється перпендикулярно силовій лінії
1. – швидкість частинки перпендикулярна магнітному полю.
Слайд 5 Особливість дрейфового руху: немає зсуву в сторону слабкого чи сильнішого
поля. Частинка, рухаючись по вузькій доріжці, в межах своєї траєкторії
має поле однакової напруженості. Це означає, що адіабатична інваріантність має місце і у випадку магнітного дрейфу.
Радіус кривизни ρ в точці М:
де ds – елемент довжини траєкторії; знак “–” відповідає зменшенню кута α при збільшенні ds.
Слайд 6 Зміщення траєкторії за один оберт:
Середня швидкість дрейфу u=Δx/T (Т –
період обертання):
Радіус кривизни ρ ~ 1 / H, тому:
Слайд 7 Враховуючи, що для неоднорідного поля, яке слабко змінюється, виконується умова:
отримаємо
співвідношення швидкостей дрейфу і обертання:
з виразу
Дрейфовий рух може бути
зумовлений і подовжньою швидкістю . Слайд 8 Дрейфовий рух може бути зумовлений і подовжньою
швидкістю
.
Напрямок такого руху такий же як и при
Дрейфовий рух виникає не тільки при неоднорідності магнітного поля, але також і тоді, коли на заряджену частинкуку в однорідному магнітному полі діє додаткова сила немагнітного походження (наприклад, з боку електричного або гравітаційного поля), спрямована перпендикулярно до вектора Н.
Слайд 9 В точці М1 вектор ,
внаслідок чого сила Лоренца рівна нулю.
Рухаючись далі по інерції частинка відхи-ляється від силової лінії (“зісковзує” з неї), що зумов-лює появу в точці М2 певного кута між векторами швидкос-ті та магнітного поля і неве- ликої складової швидкості, що є перпендикулярною до магнітного поля.
Поява появи сили Лоренца появи дрейфової швидкості, що є перпендикулярною до площини рисунка (паралельно вектору ):
2. – швидкість частинки паралельна магнітному полю.
Слайд 10 Швидкість дрейфу за умови довільної орієнтації вектора швидкості частинки
відносно напрямку неоднорідного магнітного поля в просторі без струмів можна
визначити згідно з виразом: В загальному випадку рух зарядженої частинки в неоднорідному магнітному полі є суперпозицією наступних рухів:
Позитивно і негативно заряджені частинки дрейфують в протилежних напрямках.
Обертання по ларморівському колу із швидкістю
.
Руху центра ларморівського кола вздовж силової
лінії із швидкістю ( ).
Дрейфового руху центра ларморівського кола із
швидкістю .
Слайд 11 Якщо з’єднати миттєві положення центрів ларморівського обертання, отримаємо осьову лінію
траєкторій, яку можна розглядати як усереднений рух частинки.
Рух заряджених
частинок в комбінованих полях 1. Однорідні поля.
В перпендикулярній до площині частинка буде рухатись по колу радіусом:
Вздовж осі z рух буде рівномірно прискореним (сповільненим):
В результаті траєкторія частинки буде відповідати гвинтовій лінії із змінним кроком.
Слайд 12Рух заряджених частинок під дією паралельних і антипаралельних електричного і
магнітного полів
Слайд 13 2. Однорідні поля.
Допустимо, що вісь y направлена вздовж електричного
поля, вісь z – вздовж магнітного, а початкова швидкість лежить
в площині xy. Рівняння руху: Замість x введемо нову змінну , де u – постійна. Нова система координат рухається відносно x з швидкістю u. Перепишемо рівняння руху:
Вибираємо постійну u у вигляді:
Слайд 14 Система рівнянь матиме вигляд:
Таким чином, в новій системі координат (x1,
y) частинка рухається по колу. Результуючий рух складається з рівномірного
руху вздовж осі x і обертання по колу в площині xy. Траєкторія руху – трохоїда, а при нульовій початковій швидкості v0 = 0 – циклоїда.
Якщо початкова швидкість направлена вздовж осі x і рівна v0 = сЕ/Н, трохоїда вироджується в пряму, оскільки в системі координат (x1, y) частинка є нерухомою.
Слайд 15 3. Довільна орієнтація і .
Вибираємо систему координат: вісь z – вздовж магнітного поля, вісь
y – вздовж складової електричного поля, що є перпендикулярною до магнітного. Результуючий рух складається з двох простих рухів – в площині xy і вздовж осі z. Проекція траєкторії на площину xy – трохоїда, а вздовж осі z частинка рухатиметься рівномірно прискорено (сповільнено).
Слайд 16 3. Змінне електричне поле. Циклотронний резонанс.
Якщо напруженість поперечного електричного поля
змінюється з частотою
циклотронний резонанс.
З рівнянь руху при
можна отримати: Траєкторія руху – спіраль, радіус якої зростає ~ t. Енергія частинки зростатиме ~ t2. В результаті зіткнень енергія переходить в теплову.
Метод нагріву плазми, що вперше був здійснений на токамаку ТМ-3 (Курчатовський інститут, 1971).
Слайд 17Рух у полі прямого провідника зі струмом
Напруженість магнітного поля змінюється
обернено пропорційно відстані від провідника.
а) Дрейф електрона в напрямку,
перпендикулярному до H і gradH (вздовж провідника). б) Дрейф під дією електричного поля, зумовленого падінням напруги вздовж провідника.
в) Результуючий рух.
Слайд 18Вплив магнітного поля на властивості плазми
В проміжку між двома кулонівськими
зіткненнями кожна заряджена частинка плазми, що знаходиться в магнітному полі,
рухається по гвинтовій траєкторії. Якщо поле однорідне, осьова лінія траєкторії співпадає з однією з силових ліній поля.Зміщення електронів та іонів поперек силових ліній може відбуватись лише завдяки кулонівським зіткненням (при кожному зіткненні на відстань ~ ларморівського радіусу).
Якщо зіткнення відбуваються рідко (низька густина та висока температура плазми), частинки є “прив’язаними” до силових ліній. Така плазма називається замагніченою.
Мірою замагніченості є відношення λ/ρН , де λ – довжина вільного пробігу, ρН – ларморівський радіус.
λ >> ρН (рідкі зіткнення, сильне поле) – траєкторія частинки на довжині λ встигає згорнутися в гвинтову лінію; – несуттєві зміщення поперек поля.
λ << ρН (висока густина плазми, слабке поле ) – рух частинок буде ізотропним, тобто вплив магнітного поля на властивості плазми буде несуттєвим.
Слайд 19 Критерій замагніченості:
де τ – середній час між зіткненнями (τ =
λ/v); ρН, ωН – ларморівський радіус і частота відповідно:
Замагніченість
різна для електронної та іонної компонент плазми. При однакових температурах і довжинах вільного пробігу замагніченість електронної компоненти в багато разів більша: , оскільки
Плазма замагнічена, якщо:
Слайд 20 Ситуація, коли електрони є замагніченими, а іони незамагніченими, має місце
в низькотемпературній плазмі МГД-генераторів. В такому генераторі виникає додаткове електричне
поле (поле Холла), зумовлене зміщенням заряджених частинок між зіткненнями в сильному магнітному полі в площині, що є перпендикулярною магнітному полю. У високотемпературній або достатньо розрідженій плазмі замагніченими є як електрони, так і іони. Такою є плазма в магнітних термоядерних пастках, у верхніх шарах іоносфери, сонячній короні та газових розрядах при низькому тиску.
Для плазми з
n ~ 1010 – 1014 см-3 ,
Те = Ті ~ 106 – 107 К
при Н ~ 10 ∙ 103 е параметр замагніченості
для електронів:
а для іонів водню:
Слайд 21 Внаслідок зумовлених сильним магнітним полем обмежень на рух частинок в
площині, що є перпендикулярною магнітному полю, плазму можна утримувати від
контакту зі стінками камери, в якій вона знаходиться.Ефективна термоізоляція гарячої
плазми сильним магнітним полем
Однак такий стан плазми не є рівноважним. Завдяки кулонівським зіткненням плазма за певний час розповсюдиться по всьому об’єму камери.