Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК Когда альтернативные
Содержание
- 1. 1 СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК Когда альтернативные
- 2. Однако, когда зависимая переменная отличается, этого делать нельзя. 2СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
- 3. В случае линейной модели, R2 измеряет долю
- 4. Очевидно, что они связаны, но они не совпадают, поэтому прямые сравнения бессмысленны. 4СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
- 5. Однако доброкачественность моделей с линейной и логарифмической
- 6. Это семейство спецификаций, зависящих от параметра l.
- 7. Модель нелинейна по параметрам, поэтому следует использовать
- 8. 8СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИКПричина, по которой
- 9. 9СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИКВвод l =
- 10. 10СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИКВвод l =
- 11. 11СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИКТаким образом, можно
- 12. Результатом может быть то, что один отклоняется,
- 13. когдакогда 13СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИКПреобразование Бокса–Кокса:Если вы
- 14. Первый шаг - разделить наблюдения по зависимой
- 15. Теперь вы регрессируете Y* и logeY*, оставляя
- 16. Остаточные суммы квадратов теперь прямо сопоставимы. Таким
- 17. среднее геометрическое YМы будем использовать преобразование для
- 18. Первый шаг - вычислить среднее геометрическое зависимой
- 19. Сумма логарифмов Y равна логарифму произведений Y. 19СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
- 20. Теперь мы используем правило, согласно которому alog
- 21. И, наконец, мы используем тот факт, что
- 22. LGEARN уже определен как логарифм EARNINGS. Мы
- 23. Затем мы определяем EARNSTAR, разделив EARNINGS на
- 24. Мы также определяем LGEARNST, логарифм EARNSTAR. 24СРАВНЕНИЕ ЛИНЕЙНЫХ
- 25. . reg EARNSTAR S EXP---------------------------------------------------------------------------- Source
- 26. Мы запускаем параллельную регрессию для LGEARNST. Остаточная
- 27. . boxcox EARNINGS S EXP
- 28. Однако даже значение 0 не (полностью) лежит
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 1
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Когда альтернативные характеристики регрессионной модели имеют
Слайд 2Однако, когда зависимая переменная отличается, этого делать нельзя.
2
СРАВНЕНИЕ ЛИНЕЙНЫХ И
ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Слайд 3В случае линейной модели, R2 измеряет долю дисперсии в Y,
объясненную моделью. В случае полулогарифмической модели она измеряет долю дисперсии
логарифма Y, объясненную моделью. 3
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Слайд 4Очевидно, что они связаны, но они не совпадают, поэтому прямые
сравнения бессмысленны.
4
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Слайд 5Однако доброкачественность моделей с линейной и логарифмической версиями одной и
той же зависимой переменной можно сравнить косвенно, подвергнув зависимую переменную
преобразованию Бокса–Кокса и приспосабливая показанную модель. 5
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Преобразование Бокса–Кокса:
Слайд 6Это семейство спецификаций, зависящих от параметра l. Определение l является
эмпирическим вопросом, как и определение других параметров.
6
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ
ХАРАКТЕРИСТИКПреобразование Бокса–Кокса:
Слайд 7Модель нелинейна по параметрам, поэтому следует использовать метод нелинейной регрессии.
На практике используется оценка максимального правдоподобия.
7
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Преобразование
Бокса–Кокса:Слайд 8 8
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Причина, по которой это преобразование представляет
интерес в данном контексте, заключается в том, что спецификации с
линейными и логарифмическими зависимыми переменными являются частными случаями.когда
когда
Преобразование Бокса–Кокса:
Слайд 9 9
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Ввод l = 1 дает линейную
модель. Зависимая переменная тогда Y – 1, а не Y,
но вычитание константы из зависимой переменной не влияет на результаты регрессии, за исключением оценки перехвата.когда
когда
Преобразование Бокса–Кокса:
Слайд 10 10
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Ввод l = 0 дает (полу)логарифмическую
модель. Конечно, нельзя говорить о том, чтобы ввести l ровно
равным 0, потому что тогда зависимая переменная становится нулевой, деленной на ноль. Речь идет о предельном виде, когда l стремится к нулю, и мы воспользовались правилом Лопиталя.когда
когда
Преобразование Бокса–Кокса:
Слайд 11 11
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Таким образом, можно подогнать общую модель
и посмотреть, близок ли l к 0 или близок к
1. Конечно, "близкий" не имеет значения в эконометрике. Чтобы подойти к этому вопросу технически, нужно проверить гипотезы: l = 0 и l = 1.когда
когда
Преобразование Бокса–Кокса:
Слайд 12Результатом может быть то, что один отклоняется, а другой не
отклоняется, но, конечно, возможно, что ни один из них не
отклоняется или оба отклоняются, всё зависит от выбранного вами уровня значимости. 12
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
когда
когда
Преобразование Бокса–Кокса:
Слайд 13когда
когда
13
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Преобразование Бокса–Кокса:
Если вы заинтересованы только в
сравнении соответствий линейных и логарифмических спецификаций, существует короткая процедура, которая
включает только стандартные регрессии наименьших квадратов.Слайд 14Первый шаг - разделить наблюдения по зависимой переменной на их
среднее геометрическое. Будем называть преобразованную переменную Y*.
14
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ
ХАРАКТЕРИСТИКсреднее геометрическое Y
Слайд 15Теперь вы регрессируете Y* и logeY*, оставляя правую часть уравнения
без изменений. (Параметрам были даны простые оценки, чтобы подчеркнуть, что
коэффициенты не будут оценками исходных b1 и b2.). 15
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
среднее геометрическое Y
Слайд 16Остаточные суммы квадратов теперь прямо сопоставимы. Таким образом, спецификация с
меньшим RSS обеспечивает лучшую подгонку.
16
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
среднее геометрическое
YСлайд 17среднее геометрическое Y
Мы будем использовать преобразование для сравнения приступов линейной
и полулогарифмической версий простого уравнения заработной платы, используя набор данных
EAWE Data Set 21. 17
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Слайд 18Первый шаг - вычислить среднее геометрическое зависимой переменной. Самый простой
способ сделать это - взять экспоненту среднего значения логарифма зависимой
переменной. 18
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Слайд 19Сумма логарифмов Y равна логарифму произведений Y.
19
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ
ХАРАКТЕРИСТИК
Слайд 20Теперь мы используем правило, согласно которому alog X совпадает с
выражением log Xa
20
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Слайд 21И, наконец, мы используем тот факт, что экспонента логарифма X
сводится к X.
21
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Слайд 22LGEARN уже определен как логарифм EARNINGS. Мы находим его среднее.
В программе Stata это делается с помощью команды «sum».
22
СРАВНЕНИЕ ЛИНЕЙНЫХ
И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК. sum LGEARN
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
LGEARN | 500 2.824265 .553001 .6931472 4.642948
Слайд 23Затем мы определяем EARNSTAR, разделив EARNINGS на экспоненту среднего значения
LGEARN.
23
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
. sum LGEARN
Variable |
Obs Mean Std. Dev. Min Max-------------+--------------------------------------------------------
LGEARN | 500 2.824265 .553001 .6931472 4.642948
. gen EARNSTAR = EARNINGS/exp(2.8243)
Слайд 24Мы также определяем LGEARNST, логарифм EARNSTAR.
24
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
.
sum LGEARN
Variable | Obs
Mean Std. Dev. Min Max-------------+--------------------------------------------------------
LGEARN | 500 2.824265 .553001 .6931472 4.642948
. gen EARNSTAR = EARNINGS/exp(2.8243)
. gen LGEARNST = ln(EARNSTAR)
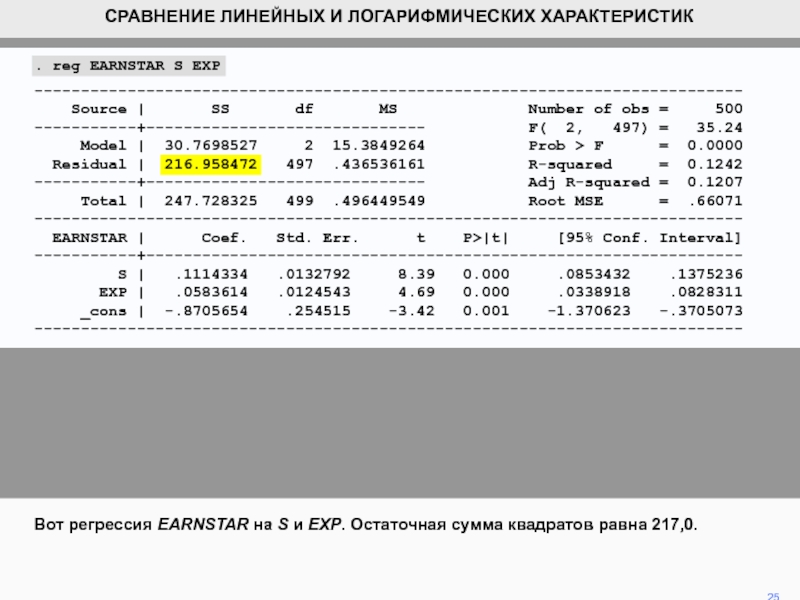
Слайд 25. reg EARNSTAR S EXP
----------------------------------------------------------------------------
Source |
SS df MS
Number of obs = 500-----------+------------------------------ F( 2, 497) = 35.24
Model | 30.7698527 2 15.3849264 Prob > F = 0.0000
Residual | 216.958472 497 .436536161 R-squared = 0.1242
-----------+------------------------------ Adj R-squared = 0.1207
Total | 247.728325 499 .496449549 Root MSE = .66071
----------------------------------------------------------------------------
EARNSTAR | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
S | .1114334 .0132792 8.39 0.000 .0853432 .1375236
EXP | .0583614 .0124543 4.69 0.000 .0338918 .0828311
_cons | -.8705654 .254515 -3.42 0.001 -1.370623 -.3705073
----------------------------------------------------------------------------
Вот регрессия EARNSTAR на S и EXP. Остаточная сумма квадратов равна 217,0.
25
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Слайд 26Мы запускаем параллельную регрессию для LGEARNST. Остаточная сумма квадратов равна
131,4. Таким образом, мы заключаем, что полулогарифмическая версия лучше подходит.
26
СРАВНЕНИЕ
ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК. reg LGEARNST S EXP
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 2, 497) = 40.12
Model | 21.2104061 2 10.6052031 Prob > F = 0.0000
Residual | 131.388814 497 .264363811 R-squared = 0.1390
-----------+------------------------------ Adj R-squared = 0.1355
Total | 152.59922 499 .30581006 Root MSE = .51416
----------------------------------------------------------------------------
LGEARNST | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
S | .0916942 .0103338 8.87 0.000 .0713908 .1119976
EXP | .0405521 .009692 4.18 0.000 .0215098 .0595944
_cons | -1.624505 .1980634 -8.20 0.000 -2.013649 -1.23536
----------------------------------------------------------------------------
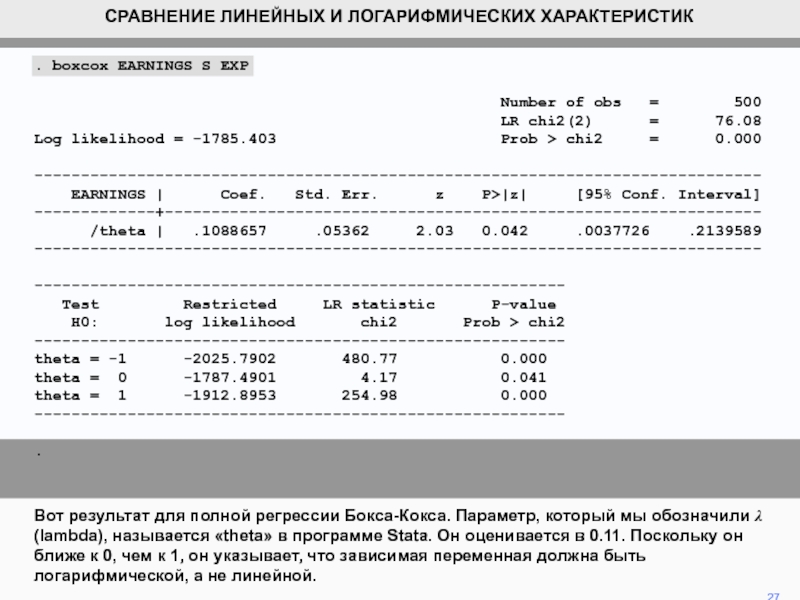
Слайд 27. boxcox EARNINGS S EXP
Number of obs = 500
LR chi2(2) = 76.08
Log likelihood = -1785.403 Prob > chi2 = 0.000
------------------------------------------------------------------------------
EARNINGS | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
/theta | .1088657 .05362 2.03 0.042 .0037726 .2139589
------------------------------------------------------------------------------
---------------------------------------------------------
Test Restricted LR statistic P-value
H0: log likelihood chi2 Prob > chi2
---------------------------------------------------------
theta = -1 -2025.7902 480.77 0.000
theta = 0 -1787.4901 4.17 0.041
theta = 1 -1912.8953 254.98 0.000
---------------------------------------------------------
.
Вот результат для полной регрессии Бокса-Кокса. Параметр, который мы обозначили l (lambda), называется «theta» в программе Stata. Он оценивается в 0.11. Поскольку он ближе к 0, чем к 1, он указывает, что зависимая переменная должна быть логарифмической, а не линейной.
27
СРАВНЕНИЕ ЛИНЕЙНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Слайд 28Однако даже значение 0 не (полностью) лежит в 95-процентном доверительном
интервале. (Тест вероятностей логарифма объясняется в главе 10.).
28
СРАВНЕНИЕ ЛИНЕЙНЫХ И
ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК. boxcox EARNINGS S EXP
Number of obs = 500
LR chi2(2) = 76.08
Log likelihood = -1785.403 Prob > chi2 = 0.000
------------------------------------------------------------------------------
EARNINGS | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
/theta | .1088657 .05362 2.03 0.042 .0037726 .2139589
------------------------------------------------------------------------------
---------------------------------------------------------
Test Restricted LR statistic P-value
H0: log likelihood chi2 Prob > chi2
---------------------------------------------------------
theta = -1 -2025.7902 480.77 0.000
theta = 0 -1787.4901 4.17 0.041
theta = 1 -1912.8953 254.98 0.000
---------------------------------------------------------
.