1 Требования к слушателям курса Отчёт по пропущенным занятиям Написание и

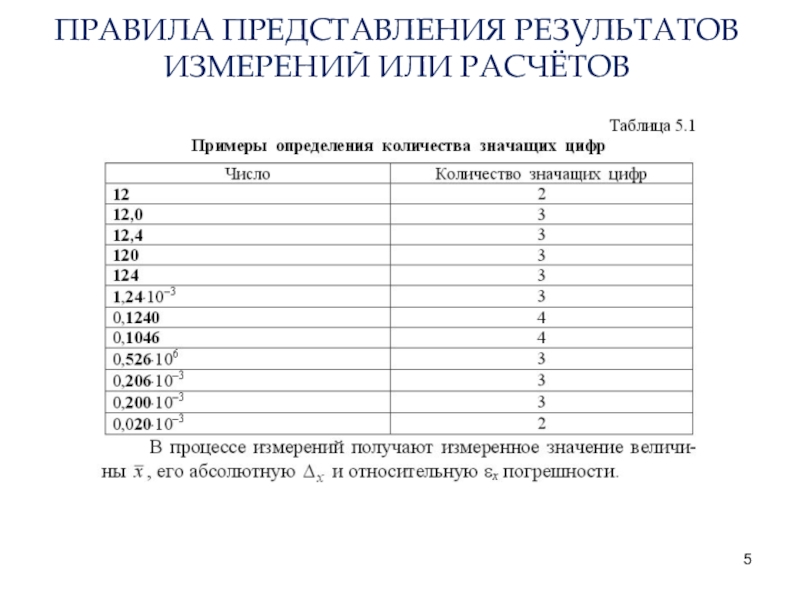
погрешностей диссертационного исследования на тему ...» (обязательно для всех)
3. Реферат

оформляется согласно СТО университета (см. сайт университета)
4. Сдавшему реферат и получившему зачёт по реферату до 15.05.2020 прощаются пропущенные занятия
5. Зачёт по курсу принимается до 25.06.2020 при условии сданного реферата
6. Аспиранты, имеющие во вкладышах оценку за курс «Численные методы...» освобождаются от посещения занятий, но подготовка реферата обязательна!.

метода
связана со способом решения задачи (относится к устранимой или

условной)
Погрешность округлений
в вычислительном эксперименте всегда используются числа с определённой точностью

отличающейся от нуля цифрой.
Примеры:
число 284 - три,
число 0,34

– две,
число 0,005706 – четыре значащие цифры

О ПОГРЕШНОСТИ ПРИБЛИЖЁННЫХ ВЫЧИСЛЕНИЙ

из отбрасываемых разрядов меньше пяти, то оставшиеся цифры не изменяются.

Например, 0,51328≈ 0,5; 0,51328≈ 0,51; 0,51328≈ 0,513.

2. Если цифра старшего из отбрасываемых разрядов больше или равно пяти, причем все последующие цифры больше нуля, то цифра младшего из сохраняемых разрядов увеличивается на единицу.
Например, 0,57862≈0,6; 0,57862≈0,58; 0,57862≈0,579;
0,58652≈0,6 ; 0,58652≈0,587.

3. Если цифра старшего из отбрасываемых разрядов равна пяти, и хотя бы две из последующих за ней цифры равны нулю или неизвестны, то цифра младшего из сохраняемых разрядов не изменяется, если она чётная, и увеличивается на единицу, если она нечётная.
Например, 0,285004≈0,28; 0,355002≈0,36.

подчиняться погрешности метода
Вычислять следует с числом значащих цифр, на

единицу превышающих их число в исходных данных, с тем, чтобы относительная погрешность результата вычислений была бы на порядок (в 10 раз) меньше погрешности исходных данных.

том, что относительная погрешность суммы положительных приближённых чисел не превосходит

максимальной относительной погрешности слагаемых.

двух приближённых положительных чисел указывает на возможность

сильного возрастания погрешности при . В этом случае говорят о потере точности при вычитании близких чисел.

необходимо иметь значения аргументов, чтобы получить значение функции этих аргументов

с заданной точностью. Это так называемая обратная задача теории погрешностей, которая заключается в оценивании величин (или ) по известной величине u.
Для случая дифференцируемой функции одной переменной грубое решение обратной задачи находится очень просто: если y=f(x), то откуда

Для функций большего числа переменных обратная задача, вообще говоря, некорректна. Нужны дополнительные условия. Например, применяют принцип равных влияний, состоящий в предположении, что частные дифференциалы в формуле (1)

(1)

одинаково влияют на погрешность значения функции; тогда

аргументов, т.е. считать
Обратная задача теории погрешностей
Из последнего равенства

получаем величину

характеризующую относительный уровень точности задания аргументов, на основе которой за границы абсолютных погрешностей аргументов принимаем

слагаемые округлены до m-го десятичного разряда
правило Чеботарёва
Пример
Принцип

А.Н.Крылова:
приближённое число должно записываться так, чтобы в нём все значащие цифры, кроме последней были верны и лишь последняя была бы сомнительна, и притом в среднем не более чем на одну единицу