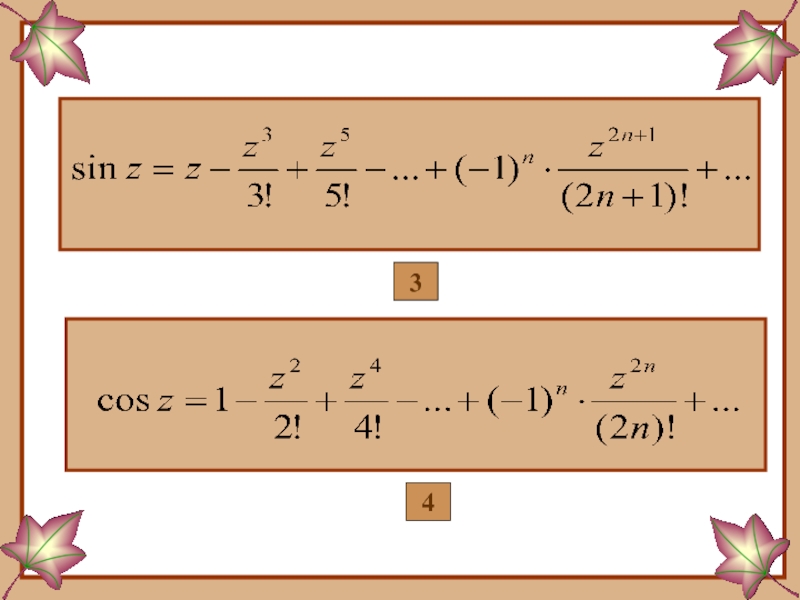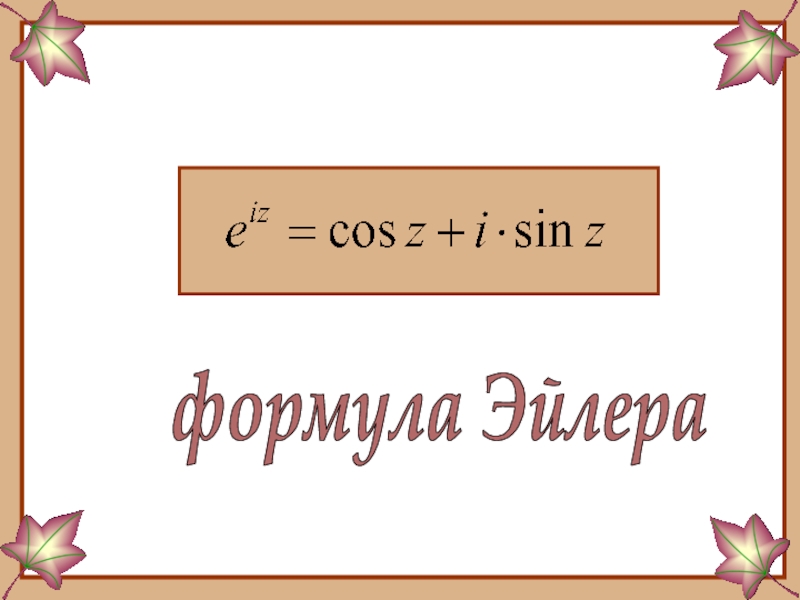Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
22.4. ПОКАЗАТЕЛЬНАЯ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО Ряд с
Содержание
- 1. 22.4. ПОКАЗАТЕЛЬНАЯ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО Ряд с
- 2. Число S называется суммой ряда:
- 3. Ряд (1) сходится тогда и только тогда,
- 4. Таким образом, из сходимости последовательности комплексных чисел
- 5. Ряд (1) сходится абсолютно, если сходится рядОпределение
- 6. 1. Показательная и тригонометрические функцииКогда показатель степени
- 7. Воспользуемся известными разложениями в ряд функций действительного аргументаи определим их для комплексного аргумента:2
- 8. 34
- 9. Ряды, стоящие в правой части равенств, сходятся,
- 10. Найдем связь между этими функциями. Подставим в
- 11. Складываем почленно полученное равенство с равенством (2):Правые
- 12. формула Эйлера
- 13. Если в формуле Эйлера заменить z на –z, тоСкладывая и вычитая почленно последние два равенства, получаем:
- 14. Эти формулы позволяют вычислять значения тригонометрических функций
- 15. Получим выражение, позволяющее вычислять значения показательной функции при любом комплексном значении показателя. Т.к.тоПо формуле Эйлераследовательно
- 16. Тогда и одно из значений аргумента равно у:
- 17. Пример.Вычислить 1234
- 18. Решение.123
- 19. 4
- 20. Из равенства следует периодичность функции с периодом 2Пi:
- 21. В частности: Поскольку показательная функция имеет период
- 22. Между тригонометрическими функциями сохраняются связывающие их тождества.
- 23. Скачать презентанцию
Число S называется суммой ряда:
Слайды и текст этой презентации
Слайд 122.4. ПОКАЗАТЕЛЬНАЯ И
ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Ряд с комплексными членами
называется
сходящимся, если существует конечный предел последовательности его частичных сумм:
Слайд 3Ряд (1) сходится тогда и только тогда, когда сходится ряд
составленный
из действительных частей членов ряда (1), и ряд
составленный из мнимых
частей членов ряда (1).Слайд 4Таким образом, из сходимости последовательности комплексных чисел следует сходимость двух
последовательностей, одна из которых состоит из действительных, а другая –
из мнимых частей комплексной последовательности.Если
то
Слайд 5Ряд (1) сходится абсолютно, если сходится ряд
Определение суммы, разности, произведения
рядов с комплексными членами такие же, как и для рядов
с действительными членами.Слайд 61. Показательная и
тригонометрические функции
Когда показатель степени является комплексным числом,
определение степени
вводимое в алгебре, теряет смысл. Аналогично, известные из
тригонометрии функциитеряют смысл при комплексном аргументе z.
Слайд 7Воспользуемся известными разложениями в ряд функций действительного аргумента
и определим их
для комплексного аргумента:
2
Слайд 9Ряды, стоящие в правой части равенств, сходятся, и притом абсолютно,
при любом комплексном значении z. Поэтому эти равенства определяют функции
во
всей плоскости комплексного переменного.При действительных значениях z эти функции будут совпадать с функциями, определенными ранее в курсе математического анализа.
Слайд 10Найдем связь между этими функциями.
Подставим в разложение (2) вместо
z величину iz.
Умножим почленно равенство (3) на i:
5
Слайд 11Складываем почленно полученное равенство с равенством (2):
Правые части этого равенства
и равенства (5) равны, следовательно можно приравнять их левые части:
Слайд 13Если в формуле Эйлера заменить z на –z, то
Складывая и
вычитая почленно последние два равенства, получаем:
Слайд 14Эти формулы позволяют вычислять значения тригонометрических функций с комплексным аргументом.
С
помощью формулы Эйлера можно перейти от тригонометрической формы комплексного числа
к показательной:показательная форма
комплексного числа