Разделы презентаций

2.6. Вывод 32 кристаллических классов (точечных групп симметрии)

Содержание

2.6.1.Первый этап – вывод кристаллических классов, в которых ось симметрии n-го порядка является единичным направлением (особым) в кристалле и добавление к ней других элементов симметрии оставляет это направление единичным.Возможные сочетания:

Слайды и текст этой презентации

Слайд 12.6. Вывод 32 кристаллических классов (точечных групп симметрии)
Эварист Галуа (1811-1832)

– основатель нового направления в математике (теории групп).

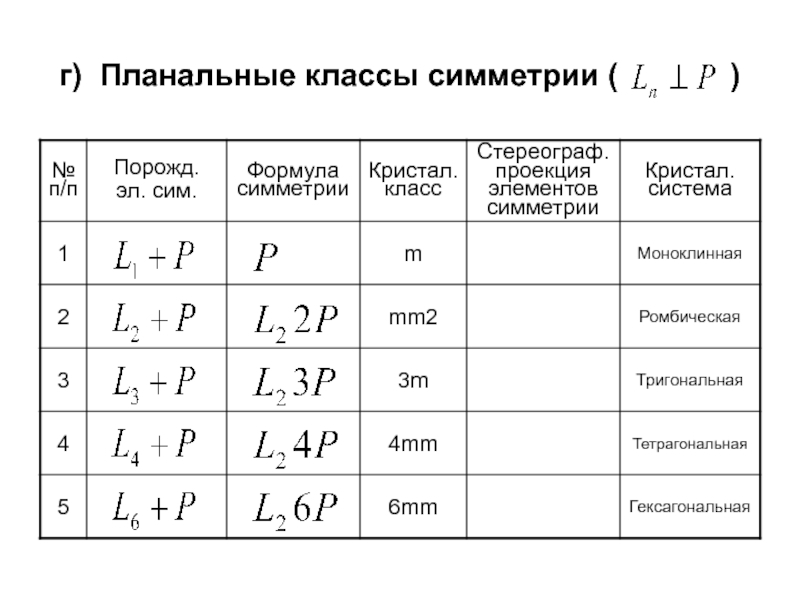
Традиционный подход:

теоремы

о сочетании элементов симметрии;
правила кристаллографической установки;
порядок записи элементов симметрии кристаллических классов.
2.6. Вывод 32 кристаллических классов (точечных групп симметрии)Эварист Галуа (1811-1832) – основатель нового направления в математике (теории

Слайд 22.6.1.Первый этап – вывод кристаллических классов, в которых ось симметрии

n-го порядка является единичным направлением (особым) в кристалле и добавление

к ней других элементов симметрии оставляет это направление единичным.

Возможные сочетания:

2.6.1.Первый этап – вывод кристаллических классов, в которых ось симметрии n-го порядка является единичным направлением (особым) в

Слайд 5а) примитивные классы симметрии

а) примитивные классы симметрии

Слайд 6б) Центральные классы симметрии (

б) Центральные классы симметрии ( )

Слайд 7в) Аксиальные классы симметрии (

в) Аксиальные классы симметрии ( )

Слайд 8г) Планальные классы симметрии (

г) Планальные классы симметрии ( )

Похожие презентации

Тема выпускной квалификационной работы: ПОЛНОЕ НАЗВАНИЕ ТЕМЫ (ПИШЕМ В КАВЫЧКАХ) Тема выпускной квалификационной работы: ПОЛНОЕ НАЗВАНИЕ ТЕМЫ (ПИШЕМ В КАВЫЧКАХ) 183
Торты, Десерты, Капкейки !!! Торты, Десерты, Капкейки !!! 277
Непосредственно образовательная деятельность по художественно-эстетическому Непосредственно образовательная деятельность по художественно-эстетическому 175
Договор доверительного управления Договор доверительного управления 409
Прыжки в длину. pptcloud.ru Прыжки в длину. pptcloud.ru 231
Типология социальных медиа Social network analysis Типология социальных медиа Social network analysis 220
Интерфейс с БД Проблемы создания БД Интерфейс с БД Проблемы создания БД 274
К О НФЕРЕНЦИЯ МЕНЕДЖЕРОВ 2019 К О НФЕРЕНЦИЯ МЕНЕДЖЕРОВ 2019 188
Здоровье - это все! Здоровье - это все! 514
доц. Орлов А.В доц. Орлов А.В 353
Лекція 4 Лекція 4 322
К 65-летию творческой жизни Евгений Евтушенко К 65-летию творческой жизни Евгений Евтушенко 240
Тема: исследование функции с помощью производной Тема: исследование функции с помощью производной 208
Малярчук Наталья Николаевна д-р. пед. наук, к-т. мед. наук заведующий кафедрой Малярчук Наталья Николаевна д-р. пед. наук, к-т. мед. наук заведующий кафедрой 250
Memorable dates of my family - Памятные даты семьи (на английском языке) Memorable dates of my family - Памятные даты семьи (на английском языке) 440
Жизнь и творчество Василия Андреевича Жуковского Жизнь и творчество Василия Андреевича Жуковского 194
Инструментарий диагностической самооценки Инструментарий диагностической самооценки 220
Рубеж веков. Павловская Россия Рубеж веков. Павловская Россия 805
2.5. Шум 2.5. Шум 235
복습 1-1 복습 1-1 185

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика