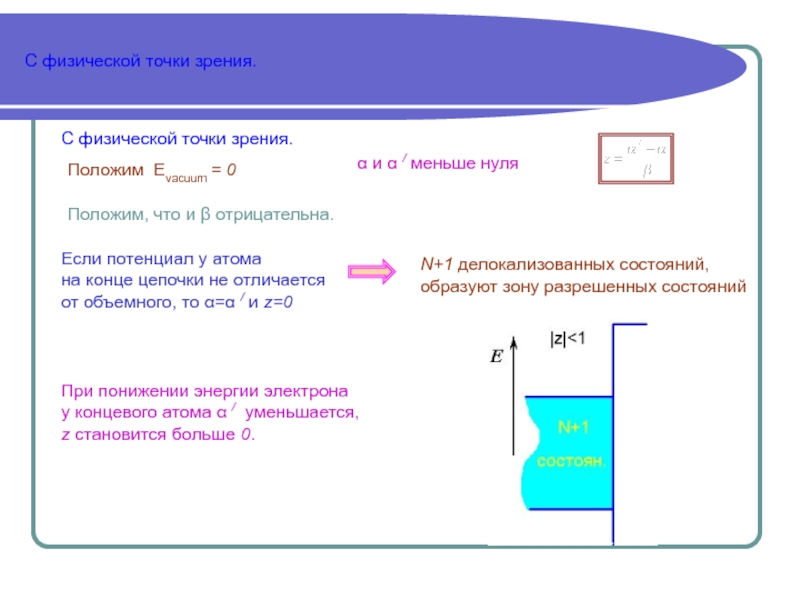
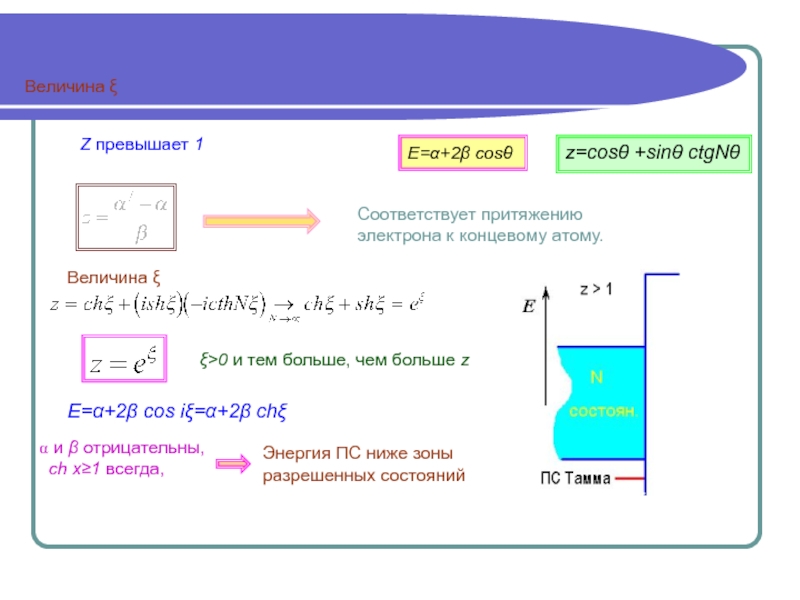
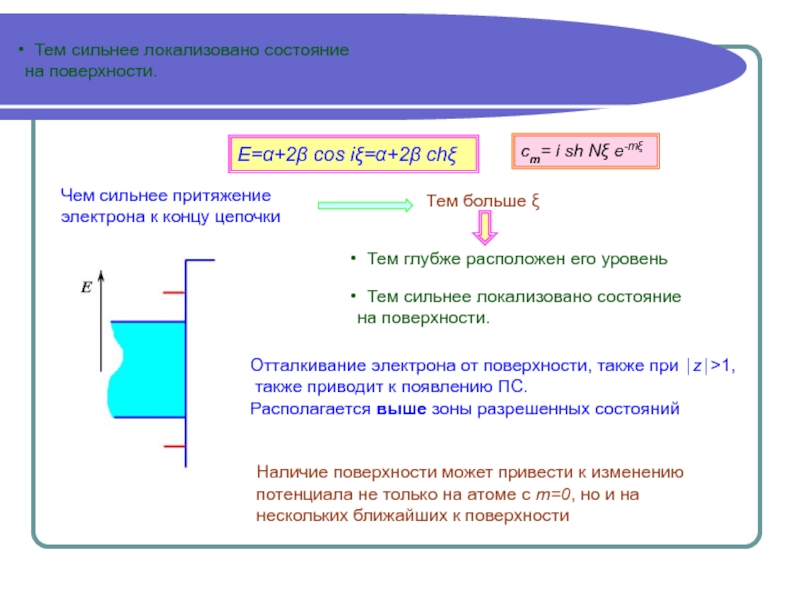
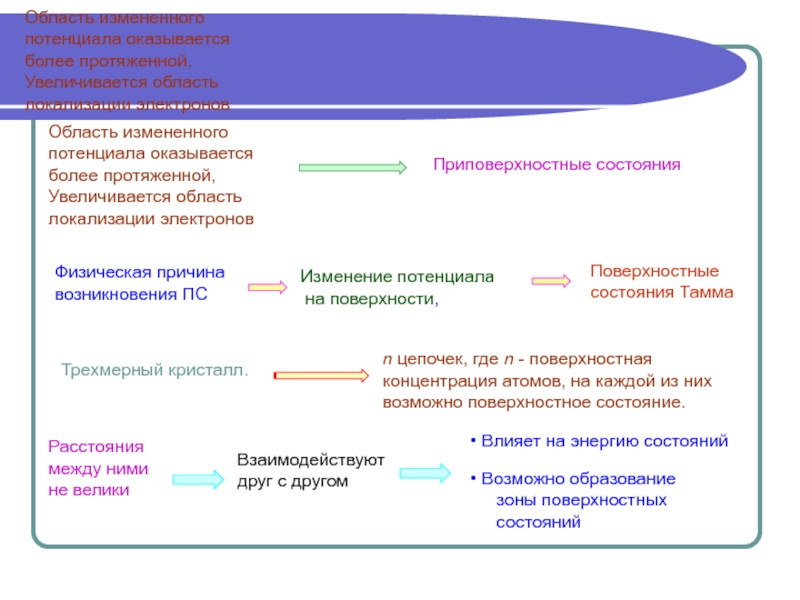
в бесконечном кристалле
Рассмотрим конечную одномерную цепочку, состоящую из N+1
атомов Необходимо найти волновые функции ψ и
собственные значения энергии ε
в виде линейной комбинации
атомных орбиталей ϕ
Метод ЛКАО
атомная орбиталь, центрированная на атоме m
случай s -атома, т.е. имеющего один электрон на внешней оболочке
cm - коэффициент, характеризующий удельный вес
m-орбитали.
На поверхности

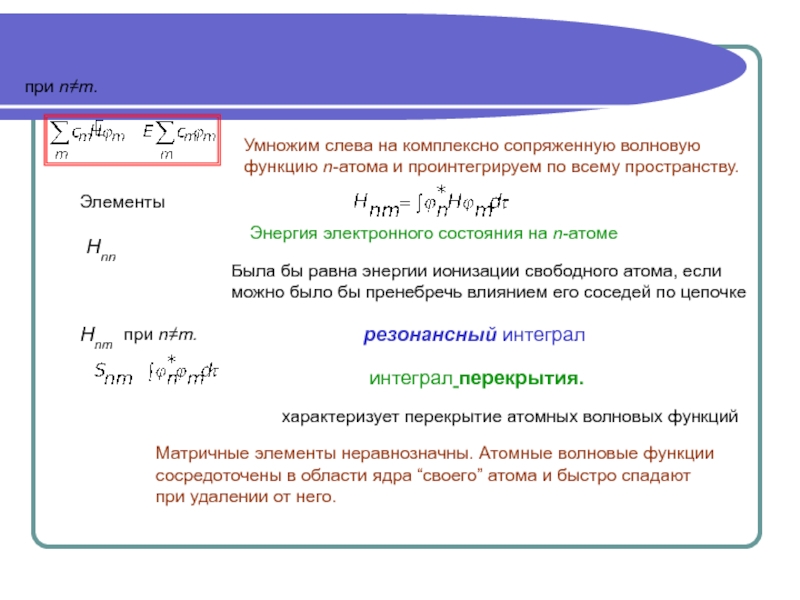
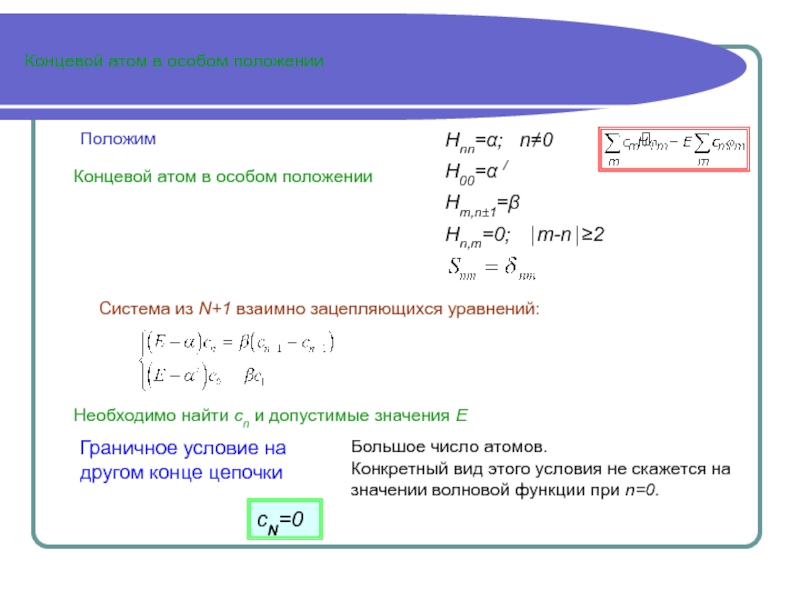
![3Поверхностные состояния. Метод ЛКАО Решение известноРешение известно - новая переменная cn=sin [(N-n)θ ]Действительно cN=sin[(N-N)θ ]=0( Решение известноРешение известно - новая переменная cn=sin [(N-n)θ ]Действительно cN=sin[(N-N)θ ]=0( E-α)sin(N-n)θ=β [sin(N-n-1)θ +sin(N-n+1)]=2β sin(N-n)θ cosθ E=α+2βcosθЧтобы](/img/thumbs/428b9e70840e2a2cd2812dfa97894915-800x.jpg)
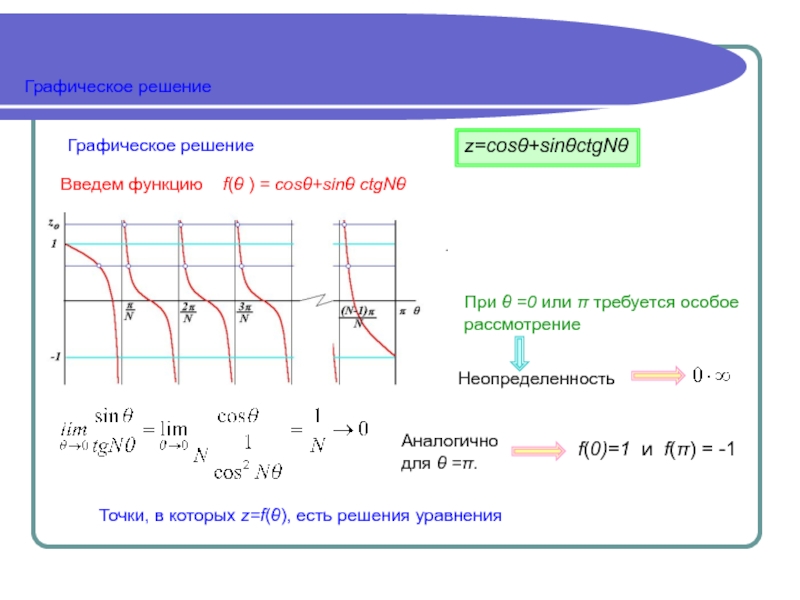

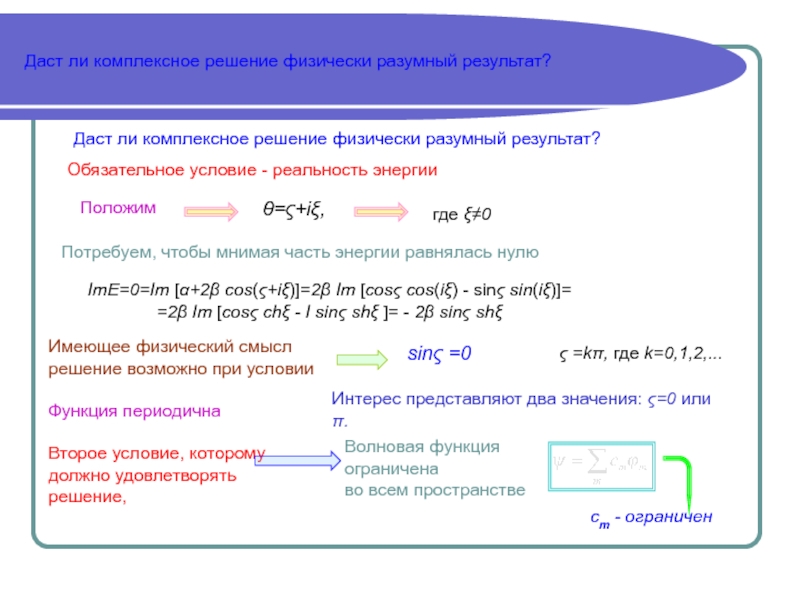
![3Поверхностные состояния. Метод ЛКАО cт= i shNξ [ch тξ - sh тξ ]=i sh Nξ cт= i shNξ [ch тξ - sh тξ ]=i sh Nξ e-тξcт= i shNξ [ch тξ -](/img/thumbs/9af636c046d47f2402cc7a45ab657683-800x.jpg)